Luo A.C.J. (Ed.) Dynamical Systems: Discontinuity, Stochasticity and Time-Delay
Подождите немного. Документ загружается.

30 Reduction on Inertial Manifolds of Navier–Stokes Equations 395
References
1. Steindl A, Troger H (2001) Methods for dimension reduction and their application in nonlinear
dynamics. Int J Solids Struct 38:2131–2147
2. Zhang JZ, Liu Y, Chen DM (2005) Error estimate for influence of model reduction of nonlin-
ear dissipative autonomous dynamical system on long-term behaviours. Appl Math Mech 26:
938–943
3. Guckenheimer J, Holmes P (1983) Nonlinear oscillations, dynamical system, and bifurcations
of vector fields. Springer, New York
4. Wiggins S (1990) Introduction to applied nonlinear dynamical systems and chaos. Springer,
New York
5. Seydel R (1994) Practical bifurcation and stability analysis: from equilibrium to chaos.
Springer, New York
6. Friswell MI, Penny JET, Garvey SD (1996) The application of the IRS and balanced realization
methods to obtain reduced models of structures with local nonlinearities. J Sound Vib 196:
453–468
7. Fey RHB, van Campen DH, de Kraker A (1996) Long term structural dynamics of mechanical
system with local nonlinearities. ASME J Vib Acoust 118:147–163
8. Kordt M, Lusebrink H (2001) Nonlinear order reduction of structural dynamic aircraft models.
Aerosp Sci Technol 5:55–68
9. Slaats PMA, de Jongh J, Sauren AAHJ (1995) Model reduction tools for nonlinear structural
dynamics. Comput Struct 54:1155–1171
10. Zhang JZ (2001) Calculation and bifurcation of fluid film with cavitation based on variational
inequality. Int J Bifurcat Chaos 11:43–55
11. Murota K, Ikeda K (2002) Imperfect bifurcation in structures and materials. Springer,
New York
12. Marion M, Temam R (1989) Nonlinear Galerkin methods. Siam J Numer Anal 26:1139–1157
13. Temam R (1997) Infinite-dimensional dynamical system in mechanics and physics. Springer,
New York
14. Titi ES (1990) On approximate inertial manifolds to the Navier–Stokes equations. J Math Anal
Appl 149:540–557
15. Jauberteau F, Rosier C, Temam R (1990) A nonlinear Galerkin method for the Navier–Stokes
equations. Comput Methods Appl Mech Eng 80:245–260
16. Schmidtmann O (1996) Modelling of the interaction of lower and higher modes in two-
dimensional MHD-equations. Nonlinear Anal Theory Methods Appl 26:41–54
17. Chueshov ID (1996) On a construction of approximate inertial manifolds for second order in
time evolution equations. Nonlinear Anal Theory Methods Appl 26:1007–1021
18. Rezounenko AV (2002) Inertial manifolds for retarded second order in time evolution equa-
tions. Nonlinear Anal 51:1045–1054
19. Laing CR, McRobie A, Thompson JMT (1999) The post-processed Galerkin method applied
to non-linear shell vibrations. Dyn Stab Syst 14:163–181
20. Zhang JZ, van Campen DH, Zhang GQ, Bouwman V, ter Weeme JW (2001) Dynamic stability
of doubly curved orthotropic shallow shells under impact. AIAA J 39:956–961
21. Foias C, Sell GR, Temam R (1985) Varietes Inertielles des Equations Differentielles Dissipa-
tives. C R Acad Sci Paris Ser I Math 301:139–141
22. Chow SN, Lu K (2001) Invariant manifolds for flows in Banach space. J Differ Equ 74:285–317
23. Foias C, Manley O, Temam R (1987) On the interaction of small and large eddies in turbulent
flows. C R Acad Sci Paris Ser I Math 305:497–500
24. Foias C, Sell GR, Titi ES (1989) Exponential tracking and approximation of inertial manifolds
for dissipative nonlinear equations. J Dyn Differ Equ 1:199–244
25. Rezounenko AV (2004) Investigations of retarded PDEs of second order in time using the
method of inertial manifolds with delay. Ann Inst Fourier (Grenoble) 54:1547–1564
26. Zhang JZ, Liu Y, Cheng DM (2005) Error estimate for the influence of model reduction of
nonlinear dissipative autonomous dynamical system on the long-term behaviors. J Appl Math
Mech 26(7):938–943
396 J.-Z. Zhang et al.
27. Zhang JZ, Liu Y, Lei PF, Sun X (2007) Dynamic snap-through buckling analysis of shallow
arches under impact load based on approximate inertial manifolds. Dyn Continuous Discrete
Impulsive Syst Ser B (DCDIS-B) 14:287–291
28. He YN, Li KT (1999) Optimum finite element nonlinear Galerkin algorithm for the Navier–
Stokes equations. Math Numer Sin 21(1):29–38 (in Chinese)
29. Ren X, Li BH, Yin XY, Gao G (2007) Calculation of airfoil flows using GAO-YONG turbu-
lence equations. J Aerosp Power 22(1):73–78 (in Chinese)
Part IV
Classic Vibrations and Control
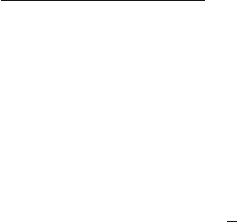
Chapter 31
Diesel Engine Condition Classification Based
on Mechanical Dynamics and Time-Frequency
Image Processing
Hongkun Li and Zhixin Zhang
Abstract In this research, mechanical structure dynamics for diesel engine working
process are investigated in detail for diesel engine vibration signal analysis and pat-
tern recognition. Time domain vibration signal can be looked on as several impulse
forces’ responses according to mechanical dynamics analysis. Different part vibra-
tion signal can be used for different components’ fault diagnoses. It is very useful
to determine the best suitable vibration signal for analysis according to structure
dynamics analysis. Hilbert spectrum is used to construct time-frequency distribu-
tion because of its performance for nonstationary signal analysis. Time-frequency
image technology is investigated in this research for diesel engine fault diagnosis.
Euclidean distance is used to distinguish engines’ different working conditions.
A single cylinder 1135 direct injection diesel engine with different working con-
ditions classification is as an example to testify the effectiveness of this method.
It can be concluded that this new approach can improve the accuracy for diesel
engine condition classification.
31.1 Introduction
Due to the complexity of mechanical systems and variation of working conditions,
diesel engines often operate in an off-design condition, which could leads to poor
performance, heavy wearing and even a breakdown of diesel engine [1]. Accurate
feature extraction and pattern recognition technology is urgently needed based on
different information, such as vibration signal, thermal parameters, etc.
Condition monitoring and fault diagnosis is very important to prevent break down
of diesel engines. Vibration signal is often used to evaluate diesel engine working
H. Li (
)
School of Mechanical Engineering, Dalian University of Technology, Dalian 116023,
People’s Republic of China
and
State Key Laboratory of Structural Analysis of Industrial Equipment, Dalian 116023,
People’s Republic of China
e-mail: lihk@dlut.edu.cn
A.C.J. Luo (ed.), Dynamical Systems: Discontinuity, Stochasticity and Time-Delay,
DOI 10.1007/978-1-4419-5754-2
31,
c
Springer Science+Business Media, LLC 2010
397
398 H. Li and Z. Zhang
condition and predict the occurrence of faults without interrupting its operation, be-
cause vibration signal contains lots of information about diesel engine condition [2].
Diesel engine vibration is a very complicated phenomenon caused by impul-
sive forces of moving components and external forces, such as cylinder combustion
pressure, valve vibration, impulsive injection pressure, initial force, which occur
simultaneously with external load disturbances. The vibration signals from cylin-
der head and cylinder block are typical nonstationary and nonlinear characteristics.
At the same time, there is much noise interference for practical monitored sig-
nal analysis. Effective feature extraction and pattern recognition are very helpful
for diesel engine fault diagnosis and preventative maintenance. Nowadays, time-
frequency technology has been broadly investigated in vibration signal analysis.
It has been testified for effectiveness in nondestructive evaluation applications.
Among them, Wigner–Ville distribution, Wavelet analysis, and a recently developed
method, Hilbert spectrum (HS), have been broadly investigated [2, 3].
In this research, HS is used to construct time-frequency image for diesel engine
pattern recognition. Experimental data of a DI135 diesel with different conditions is
used to evaluate the improved methodology for system pattern recognition and fault
diagnosis. According to the result analysis, it can be concluded that this method is
very promising for diesel engine preventative maintenance.
31.2 Diesel Engine Structure Dynamics
Diesel engine’s work in complicated conditions. There are many impulse forces
during its working condition. Complex physical and chemical processes will hap-
pen during the combustion process. At the same time, the movement of valves
and pistons make the signals fluctuate during a working cycle and the difference
in the max amplitude for cylinder head vibration signal. Thus, it is very necessary to
divide different impulse forces during its working condition for the monitored vibra-
tion signal analysis. Figure 31.1 shows the piston–crank working condition. During
one working cycle, the crank will rotate twice for a four-stroke diesel engine. It
contains intake stroke, compress stroke, combustion stroke, and exhaust stroke. In
every working stroke, there are different impulses for diesel engine cylinder head
and cylinder body. The surface vibration signal is the combination of response for
the different impulses. It can be used to analyze engine working condition. Diesel
engine vibration analysis has been broadly used for its pattern recognition.
Diesel engine vibration signal belongs to typical nonstationary and nonlinear
signal. It is the response from its internal impulse forces. Among them, Cylinder
pressure is a very important parameter for diesel engine working conditions estima-
tion. But it is also very difficult to determine in real condition because it cannot give
quantitative description.
Cylinder pressure is directly related with the combustion process in a working
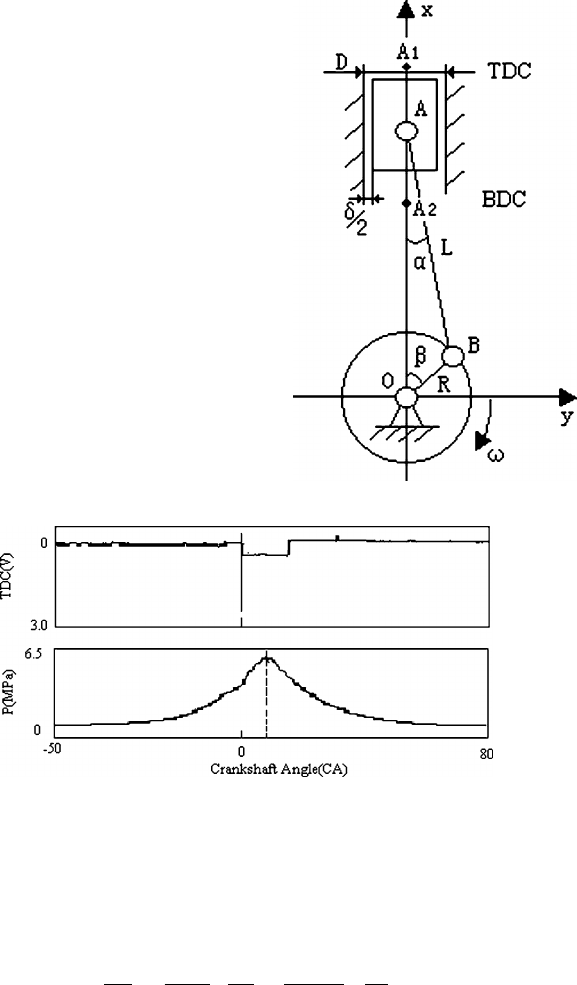
cycle. The heat released with cylinder pressure and crank angle can be expressed
with (31.1). The pressure with crank angle relationship is shown in Fig. 31.2.
31 Mechanical Dynamics and Time-Frequency Image Processing 399
Fig. 31.1 Sketch map about
the structure
Fig. 31.2 Sketch map of cylinder pressure
The maximum cylinder pressure will be after top dead centre (TDC). Although
cylinder pressure is very useful for pattern recognition, the difficulty for monitoring
limits its application.
dQ
d
D
1
p
dV
d
C
1
. 1/
V
dp
d
(31.1)
At the same time, vibration signal is closely related with cylinder pressure, which
can be used to reflect engine working condition. For a single-cylinder diesel

400 H. Li and Z. Zhang
Fig. 31.3 Cylinder head vibration signal of singe diesel
engine, the vibration signal monitored on the cylinder head is shown as Fig. 31.3.
The TDC information can give time domain information for the vibration signal.
It is much convenient for practical vibration signal analysis. Vibration signal time
information can be changed from time domain to angle domain, which is more
suitable to practical vibration signal analysis. During one working cycle, there
are four vibration responses corresponding to impulse forces shown in Fig. 31.3b.
They are combustion process impulse (CPI) responses, which contain fuel injection
impulse and combustion cylinder pressure impulse, exhaust valve close (OVC)
impulse response, throttle force impulse (TI) response, and inlet valve close (IVC)
response. Different impulse is corresponding to vibration signal. Thus, it can be
used to separate vibration signal for feature extraction and fault diagnosis [4].
Obviously, different impulse response vibration signal can be used to classify
different fault. If there is a fault in the inlet valve, it is very important to analyze
IVC vibration signal. But if there is a fault in the combustion process, it is very
important to analyze the CPI vibration signal. The combustion process contains lots
of information. It is directly corresponding to diesel engine cylinder pressure and
performance. Thus, combustion process vibration signal is used to diesel engine
classification in this research.
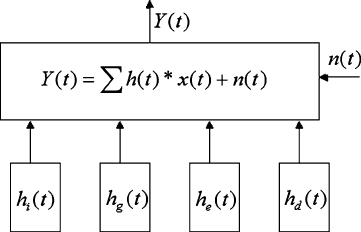
Mathematically, the relationship between a vibration signal Y.t/of a linear time-
invariant system and its signal vibration source X.t/ can be expressed by (31.2).
Y.t/ D h.t/
X.t/ (31.2)
Where: h.t/ is the impulse response of X.t/ and symbol denotes convolution of
two functions. It can be further expressed as (31.3).
Y.t/ D h
i
.t/
I.t/ C h
g
.t/
P.t/C h
e
.t/
E.t/ C h
d
.t/
D.t/ C n.t/ (31.3)
The vibration of an engine cylinder head can be simplified as a linear system of
multi-inputs and single output as shown in Fig. 31.4.InFig.31.4, h
i
.t/; h
g
.t/; h
e
.t/;
31 Mechanical Dynamics and Time-Frequency Image Processing 401
Fig. 31.4 Model of cylinder
head vibration
h
d
.t/ stand for the response paths of vibrations caused by combustion pressure
impulsive response function, exhaust valve closing impulsive response function
impact, throttle impulsive response function, and inlet valve closing impulsive
response function. At the same time, the vibration signals generated by impulse
forces follow fixed time regularity in every engine working cycle. Thus, the im-
pulse response functions in the time domain can be separated and their individual
characteristics studied.
31.3 Classification by Time Frequency Image
31.3.1 Hilbert Time-Frequency Spectrum
It is obvious that diesel engine vibration signal is full of nonstationary characteris-
tics. Traditional method, such as Fourier transform, is not enough to satisfy diesel
engine vibration signal analysis. Time frequency distribution method should be used
for its analysis. As stated above, Hilbert spectrum is used in this research for diesel
engine vibration signal analysis. To get a meaningful Hilbert spectrum, a new signal
decomposition method was introduced by Huang named as empirical mode decom-
position [3]. In 2000, Professor Ma put forward a new signal analysis theory, named
as local wave method, which is the development of EMD and HS [5]. For an arbi-
trary time series, X.t/, original data is decomposed to n intrinsic mode components
C
i
.t/ and a residual component r
n
as (31.4) according to empirical mode decompo-
sition (EMD).
X.t/ D
n
X
iD1
C
i
.t/ C r
n
.t/ (31.4)
After obtaining each IMF component, (31.5) can be deduced by using Hilbert
transform. It gives both the amplitude and the frequency of the real part of each
component as a function of time.

402 H. Li and Z. Zhang
X.t/ D RP
n
X
j D1
a
j
.t/e
i
j
.t/
D RP
n
X
j D1
a
j
.t/e
i
R
!
j
.t/t
(31.5)
Both the amplitude and the instantaneous frequency can be represented in a three-
dimensional plot, in which the amplitude can be contoured on a time-frequency
plane. The TFD of the amplitude is expressed by the Hilbert spectrum, H.!;t/,as
shown in (31.6).
H.!; t/ D RP
n
X
j D1
a
j
.t/e
i
R
!
j
.t/t
(31.6)
HS is developed from instantaneous frequency. It is very suitable for nonstationary
signal analysis. As for diesel engine working process, its vibration signal is full of
nonstationary characteristics. Thus, it can be used for vibration signal analysis and
condition classification.
At the same time, the Hilbert time-frequency spectrum can be also looked as
a two-dimension image. Nowadays, image classification has broadly used on face
classification. It has been investigated and applied in other areas, which can help
solve many practical problems. It will be helpful by using image recognition on
time-frequency distribution analysis [6]. Image classification technology can be
used to recognize diesel engine working condition.
31.3.2 Euclidean Distance
There are many methods for image analysis and classification. Among them,
Euclidean distance (ED) is greatly investigated and used in image analysis because
of its simplicity. In mathematics, the Euclidean distance or Euclidean metric is the
“ordinary” distance between two points that one would measure with a ruler, which
can be proven by repeated application of the Pythagorean theory. By using this
formula as distance, Euclidean space becomes a metric space.
The ED between points P D .p
1
;p
2
;:::;p
n
/ and Q D .q
1
;q
2
;:::;q
n
/,in
Euclidean n-space, is defined as:
ED D
p
.p
1
q
1
/
2
C .p
2
q
2
/
2
CC.p
n
q
n
/
2
D
v
u
u
t
n
X
iD1
.p
i
q
i
/
2
(31.7)
For two time-frequency images XI.m; n/ and YI.m; n/, the ED can be calculated
according to (31.8).
ED D
v
u
u
t
m
X
iD1
n
X
j D1
.XI.i; j / YI.i; j //
2
(31.8)
31 Mechanical Dynamics and Time-Frequency Image Processing 403
In (31.8), XI and YI are the standard time-frequency image and undetermined image.
ED is the distance between the two images. The smaller the ED, the similar the two
images [7].
In practical question analysis, ED
min
D min.ED
m
/. If ED is satisfied with some
scope, it can be looked as the two images are identical. That means the engine is
working with standard condition. Therefore, a threshold value ED
Th
is determined
to define the relationship between test sample and standard image. If ED
Th
> ED
min
,
it means the test sample is same as the standard image. Otherwise, it means that they
are in a different working condition.
31.3.3 Condition Classification
As stated above, mechanical dynamics is used to determine the vibration signal for
analysis in this research. Then, Hilbert spectrum is calculated to construct time-
frequency image. Euclidean distance is used to classify time-frequency image for
diesel engine pattern recognition. Thus, a quantitative description for machine con-
dition can be determined by the above method.
31.4 Example Analysis
To testify the effectiveness of this developed method, a single cylinder diesel engine
is used to simulate different working condition for pattern recognition. The exper-
iment was carried on in a lab of Institute of Internal combustion engine, Dalian
University of Technology. The testing platform is a single cylinder, direct injection
diesel engine. There are four simulated working conditions for pattern recognition.
31.4.1 Experiment
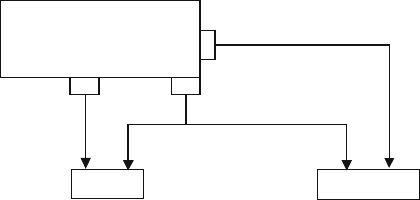
The data monitoring system is shown in Fig. 31.5. The main technical parameters of
the experimental engine are shown in Table 31.1.
DI 135 Diesel engine
Vibration sensor
PDM-2000
CBB366
Cylinder
Pressure
TDC Signal
Fig. 31.5 Sketch map of data acquisition for experiment
