Лукашин Ю.П. Адаптивные методы краткосрочного прогнозирования временных рядов

Подождите немного. Документ загружается.

ли

второго порядка превышают значения входного ряда, а

затем приближаются к ним.

При

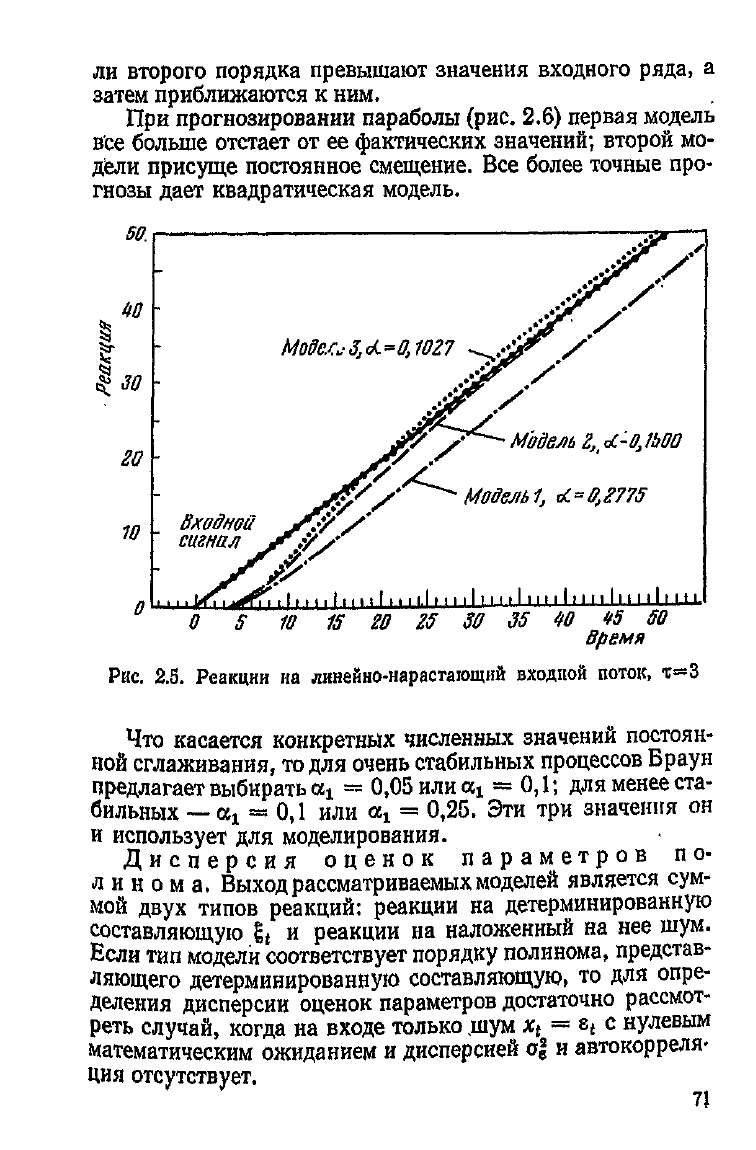
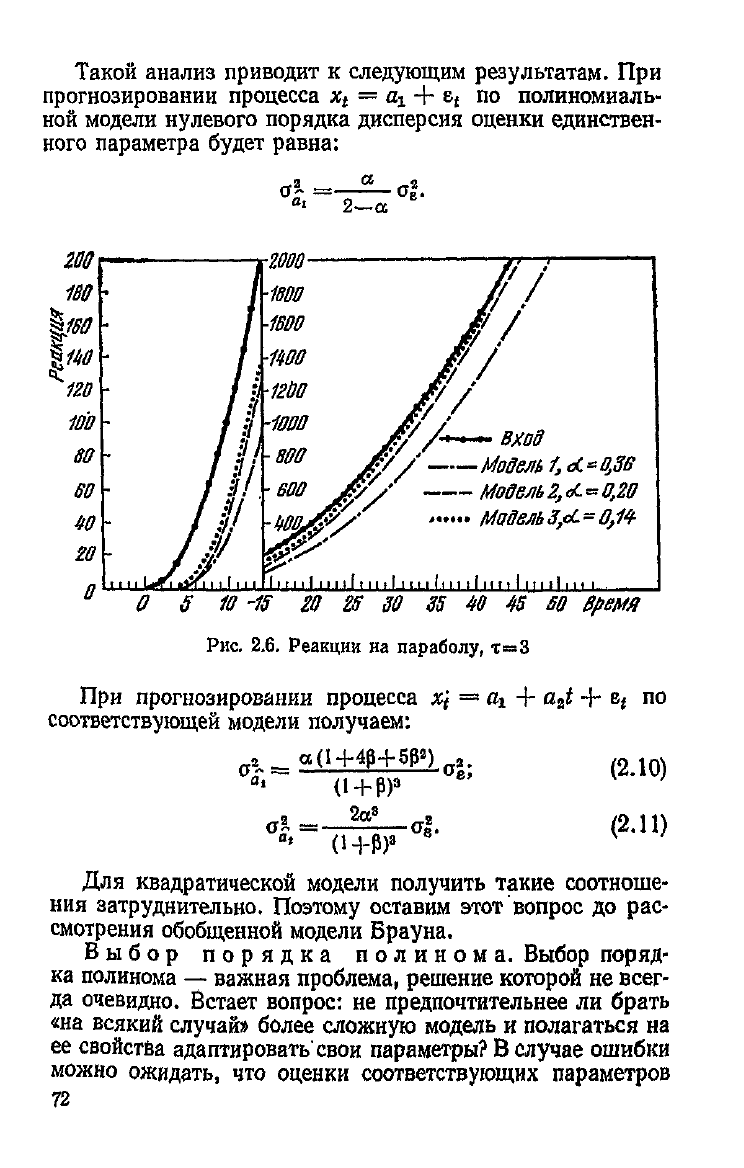
прогнозировании параболы

(рис.

2.6) первая модель

все больше

отстает

от ее фактических

значений;

второй мо-

дели присуще постоянное смещение. Все более точные про-

гнозы

дает

квадратическая модель.

Рис.

2.5. Реакции на линейно-нарастающий входной поток, т=3

Что касается конкретных численных значений постоян-

ной

сглаживания,

то

для очень стабильных процессов Браун

предлагает выбирать а

— 0,05

или

ai = 0,1; для

менее

ста-

бильных ~а

- 0,1 или а

= 0,25. Эти три значения он

использует для моделирования.

Дисперсия

оценок параметров по-

линома.

Выход

рассматриваемых моделей является сум-

мой

двух

типов реакций: реакции на детерминированную

составляющую % и реакции на наложенный на нее шум.

Если

тип модели

соответствует

порядку

полинома,

представ-

ляющего детерминированную составляющую, то для опре-

деления дисперсии оценок параметров достаточно рассмот-

реть случай, когда на

входе

только .шум x

= е

с нулевым

математическим ожиданием и дисперсией о| и автокорреля-

ция

отсутствует.

Такой

анализ приводит к следующим результатам. При

прогнозировании

процесса x

= ах +

по полиномиаль-

ной

модели нулевого порядка дисперсия оценки единствен-

ного

параметра

будет

равна:

При

прогнозировании процесса х\ — а

+ a

t + в< по

соответствующей модели получаем:

(2.10)

(2.11)

Для квадратической модели получить такие соотноше-

ния

затруднительно. Поэтому оставим этот вопрос до рас-

смотрения

обобщенной модели Брауна.

Выбор порядка полинома. Выбор поряд-

ка

полинома — важная проблема, решение которой не всег-

да очевидно. Встает вопрос: не предпочтительнее ли брать

«на всякий

случай»

более сложную модель и полагаться на

ее свойства адаптировать'свои параметры? В случае ошибки

можно

ожидать, что оценки соответствующих параметров

полинома

будут

стремиться к нулю, оказывается, что по-

ступать

так довольно опрометчиво. Дж.Д. Кохен [52] рас-

смотрел случай, когда для стационарного процесса с по-

стоянным

уровнем и нулевой корреляцией для лагов,

отличных от нуля, была ошибочно выбрана адаптивная по-

линомиальная

модель первого порядка. В этом

случае

в за-

висимости от а дисперсия ошибки прогноза на

шаг лежит

между

а%

4о%.

Для того же процесса модель

экспоненци-

альной

средней

дает

дисперсию ошибки в пределах

о%

—

—•

2о%.

ростом х ошибка более общей модели

будет,

конеч

но,

еще больше.

Выбирать

структуру

модели

следует

на основе визуаль-

ного анализа графика процесса, априорных

знаний

характе-

ра и законов развития явления, метода проб.

Следящий

контрольный

сигнал

Для скорейшего обнаружения неадекватности модели

реальному процессу, что необходимо для внесения соответ-

ствующих

изменений в модель прогнозирования, Р. Браун

[47] разработал способ анализа прогнозирующей системы,

состоящий

в подсчете величины следящего контрольного

сигнала. Следящий контрольный сигнал Kt определяется

как

сумма ошибок прогнозирования e

деленная на вели-

чину их сглаженного абсолютного значения:

т.е.

где 0 < у < 1 — постоянная сглаживания.

Браун

указывает значения критических уровней конт-

рольного сигнала,

превышение

которых говорит о необходи-

мости дополнительного изучения и изменения модели.

Такой

прием имеет два недостатка. Во-первых, в

случае

когда контрольный сигнал вышел за установленные преде-

лы,

он не обязательно вернется в эти же пределы,

даже

если

рассматриваемый процесс вновь

будет

развиваться по преж-

ним

законам и прогнозирующая модель окажется адекват-

ной

реальному процессу. Следовательно, потребуется вме-

шательство, чтобы сделать

сумму

ошибок снова близкой к

нулю

и избежать таким образом ложных сигналов тревоги.

Во-вторых,

возможна и обратная ситуация, когда конт-

рольный

сигнал

выходит

из указанных пределов, а система

начинает давать более точные прогнозы. Например, если с

некоторого момента имеют место совершенные прогнозы,

то среднее абсолютное отклонение

будет

стремиться к ну-

лю, в то время как сумма ошибок остается

неизменной.

Та-

ким

образом, контрольный сигнал

будет

стремиться к бес-

конечности.

Д.

Тригг [104] предложил простую модификацию пра-

вила Брауна, преодолевающую эти недостатки.

Вместо,

сум-

мы

ошибок он использовал сглаженную ошибку %

Следящий

контрольный сигнал Kt определяется отношени-

ем

Если

прогнозирующая система окажется настолько не-

адекватной изучаемому процессу, что все ошибки

будут

од-

ного знака, то контрольный сигнал

будет

стремиться к

или —1 (выйти за эти пределы он не может). Если из-

вестно,

что прогнозирующая система адекватна реальному

процессу и полученные ошибки

образуют

неавтокоррели-

рованную, нормально распределенную

случайную

последо-

вательность с нулевым средним и стандартным отклонением

с, то для контрольного сигнала

могут

быть определены до-

верительные интервалы.

Уравнение для сглаженной ошибки можно переписать

виде:

ее дисперсия

будет

равна

сумме

дисперсий отдельных чле-

нов:

Так

как 0 < (1 — у) < ], то при t -у

<х>

этот ряд

сходит-

ся

и его сумма равна:

Пределы для сглаженной ошибки, определяемые вели-

чиной

2о^, равны, поэтому

Для v = 0,1 получим

±0,55,

т. е. с вероятностью 95%

— 0,55 ^ Kt < + 0,55.

...

Пределы в

3(Т/<

(соответствующие вероятности 99%) при

том же значении у составят — 0,83 <1 Kt < + 0,83.

Для

значений

у, которые

не

очень

малы,

эти

рассуждения

теряют справедливость, и доверительные интервалы целе-

сообразно получать

путем

моделирования методом Монте-

Карло.

Таблицы вероятностей 2.3

2.4 Для однократного

двой-

ного экспоненциального сглаживания были получены

М. Бэтти [391.

75'

Известно,

что 0 « 1,2 среднего абсолютного отклонения.

Если 7 Достаточно мало, то можно принять, что локальная

оценка

среднего абсолютного отклонения относительно по-

стоянна

и приблизительно равна истинному среднему аб-

солютному отклонению, т. е. равна -^.

Таким

образом, при малых у, при принятых допущениях

относительно e

величина e

является случайной, нормально

распределенной, a

приблизительно постоянной величи-

ной.

Это

дает

возможность (несмотря на то, что —1 < Kt ^

а.

Н-

1) аппроксимировать распределение Kt — ^- нор-

мальным распределением.

Следовательно, пределы для контрольного сигнала, оп-

ределяемые величиной 2(Тк, приблизительно равны

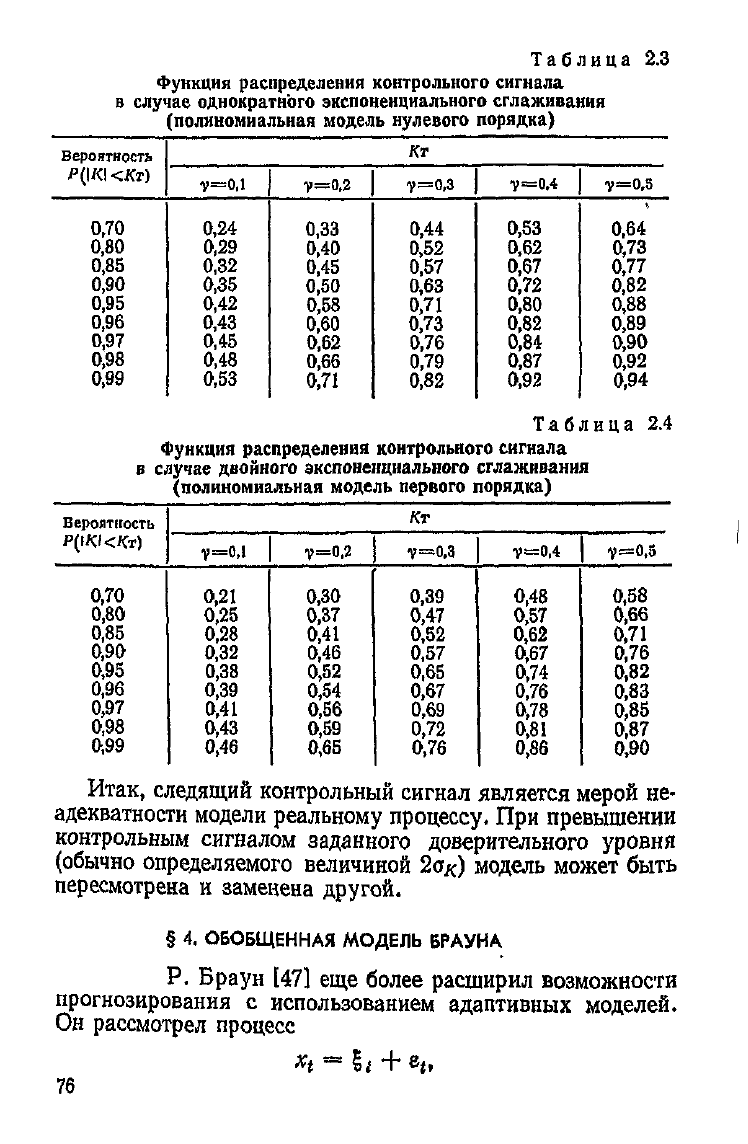
Таблица 2.3

Функция распределения контрольного сигнала

случае

однократного экспоненциального сглаживания

(полиномиальная модель

нулевого

порядка)

2.3

Вероятность

Я(|/<1

<Кт)

0,70

0,80

0,85

0,90

0,95

0,96

0,97

0,98

0,99

Кт

v=o,i

0,24

0,29

0,32

0,35

0,42

0,43

0,45

0,48

0,53

1>=0,2

0,33

0,40

0,45

0,50

0,58

0,60

0,62

0,66

0,71

V=0,3

0,44

0,52

0,57

0,63

0,71

0,73

0,76

0,79

0,82

V=0,4

0,53

0,62

0,67

0,72

0,80

0,82

0,84

0,87

0,92

7=0.5

0,64

0,73

0,77

0,82

0,88

0,89

0,90

0,92

0,94

Таблица 2.4

Функция распределения контрольного сигнала

случае

двойного экспоненциального сглаживания

(полиномиальная модель первого порядка)

Вероятность

Р(\К1<Кт)

0,70

0,80

0,85

0,90

0,95

0,96

0,97

0,98

0,99

Кт

v=o,i

0,21

0,25

0,28

0,32

0,38

0,39

0,41

0,43

0,46

V=0,2

0,30

0,37

0,41

0,46

0,52

0,54

0,56

0,59

0,65

7=0,3

0,39

0,47

0,52

0,57

0,65

0,67

0,69

0,72

0,76

V=0,4

0,48

0,57

0,62

0,67

0,74

0,76

0,78

0,81

0,86

V=0,5

0,58

0,66

0,71

0,76

0,82

0,83

0,85

0,87

0,90

Итак,

следящий контрольный сигнал является мерой не-

адекватности модели реальному процессу. При превышении

контрольным

сигналом заданного доверительного уровня

(обычно

определяемого величиной 2а

) модель может быть

пересмотрена и заменена другой.

ОБОБЩЕННАЯ

МОДЕЛЬ

БРАУНА

Р.

Браун [47] еще более расширил возможности

прогнозирования

с использованием адаптивных моделей.

Он

рассмотрел процесс

где

— случайная неавтокоррелированная величина со

средним значением 0 и дисперсией

о%;

(t)

— некоторые известные, выбранные заранее детерми-

нированные

функции от времени;

—

коэффициенты,

подлежащие определению и адап-

тации.

Рассматриваемый процесс может иметь слабые случай-

ные изменения одного или более коэффициента. Р. Браун

задался целью разработать адаптивную процедуру для пере-

смотра оценок коэффициентов при каждом получении но-

вой фактической точки ряда. Ему

удалось

построить ком-

пактную итеративную модель для случая, когда функции,

входящие в модель, удовлетворяют соотношению

где

L—-матрица постоянных коэффициентов размерностью

(п-п),

названная Р. Брауном матрицей перехода.

Такие

функции

являются решениями линейных разност-

ных уравнений. Ими

могут

быть лишь полиномы, экспонен-

ты и синусоиды или их произведения. Имея матрицу пере-

хода

для соответствующего набора функций, использован-

ных в модели, необходимо также определить значения функ-

ций

в какой-либо начальный момент времени, обычно при

t = 0 или t ~ 1. По вектору начальных значений и матри-

це

можно получить значения f

(t)

для любого момента вре-

мени

Для упрощения расчетов Р. Браун за начало отсчета

времени принимает текущий момент Т, т. е. момент состав-

ления

прогноза, За критерий ошибки, который

следует

ми-

нимизировать, взята взвешенная сумма квадратов отклоне-

ний:

где

—дисконтирующий фактор,

0<ß<l.

Далее для подбираемых

функций

вводится

(it'ti)

матрица

(t) с элементами:

(t) может быть подсчитана рекурсивно:

Здесь проявляется одно полезное свойство принятого

способа отсчета времени. Когда подбираемые функции яв-

ляются тригонометрическими или полиномами и 0 < ß < 1,

то ß' стремится к нулю быстрее, чем они

могут

расти, так

что матрица F (t) стремится к стабильному значению и ее

обратная матрица \ которая понадобится позже, при до-

статочно большом t рассчитывается один раз и уже не пере-

сматривается.

Для определения оценок коэффициентов модели в соот-

ветствии с выбранным критерием Р. Браун вывел п-компо-

нентный

вектор

где F — матрица функций в стабильном состоянии.

Так как ни одна из подбираемых функций ft (t) не является

линейной

комбинацией остальных (желательно, чтобы они были

ортогональными, т. е. чтобы У, U (t) fk (t) =0 для

всех

пар IФ k),

то F

будет

иметь обратную матрицу F-

его помощью адаптивные

коэффициенты

щ должны об-

новляться по формуле

(2.12)

где V — транспонированная матрица L;

(t — 1) — ошибка прогноза, рассчитанного в момент

t —

на 1 шаг вперед.

Константы hi зависят только от частного набора подби-

раемых функций, от вектора начальных значений f (0) и от

величины ß.

Из

(2.12)

видно, что

даже

при отсутствии ошибок прог-

нозирования

коэффициенты

будут

изменяться по закону

Это связано с

переносом,

начала отсчета времени на каж-

дом шаге на 1 интервал вперед. Второе слагаемое в

(2.12)

дает

правило корректирования коэффициентов в зависимо-.

сти от ошибки прогноза.

Исследуя дисперсию прогнозов, Р. Браун установил,

что модели, состоящие из тригонометрических функций и

постоянной

составляющей, характеризуются примерно од-

ной

и той же дисперсией прогнозов для

всех

периодов про-

гнозирования т. При

грубой

прикидке для этих моделей

можно использовать соотношение

Здесь так же, как в

вводится

понятие

эквивалентной

постоянной

сглаживания, определяемой соотношением

где п — число искомых

коэффициентов.

Для моделей, содержащих возрастающие от времени

полиномиальные члены, дисперсия прогнозов зависит от

времени упреждения т. Для небольших значений эквива-

лентной постоянной сглаживания а

—

— ß* дисперсия

прогноза по полиномиальной модели первого порядка про-

порциональна периоду прогнозирования

а для прогноза по полиномиальной модели второго порядка

она

квадратично возрастает от г:

Отметим, что в предельном случае, при

Т->-оо,

обобщен-

ная

модель Р. Брауна, содержащая только полиномиаль-

ные

функции,

в точности совпадает с рассмотренными выше

моделями многократного сглаживания того же порядка.

Для десяти моделей Р. Брауном разработаны подроб-

ные таблицы, 5 из них (табл.

2.5—2.9)

здесь приводятся.

Дисперсии в таблицах измерены в единицах а§. Отметим,

что для получения дисперсии ошибки прогноза нужно к дис-

персии

прогноза добавить а%. Все данные приведены для

трех

специфических значений эквивалентной постоянной.

Низкое

значение ß

= 0,75, т. е. ß" = 0,75, рекомендует-

ся

использовать при необходимости быстрой адаптации

оценок

коэффициентов. Среднее значение ß

= 0,90. Высо-

кое

значение

дисконтирующего фактора ß

соответствует

0,95 и обычно используется при несильном изменении

коэффициентов

«генерирующего»

процесса.

Под

кумулятивным прогнозом в таблицах понимается

сумма прогнозов для периодов упреждения от 1 до т, т. е.

Начальный

вектор коэффициентов а

должен быть по-

лучен методом взвешенной множественной регрессии на ос-

нове достаточно большого числа данных о процессе, а вы-

бор функций fi (f) осуществляется путем сопоставления

свойств элементарных функций с особенностями реального

процесса. Причем если подбираемые функции являются

тригонометрическими, то для каждой гармоники

следует

включать как синус, так и косинус. Адаптация оценок

коэф-

фициентов

осуществляется по уравнению (2.12),

Рассмотренный метод, строго говоря, правомерен толь-

ко

в установившемся состоянии. Заслуга Р. Брауна в том,

что он первый показал, возможность построения адаптив-

ных моделей, способных описывать периодические колеба-

тельные процессы.

В гл. 7, где изучаются процессы интегрированной авто-

регрессии — скользящего среднего,

будет

показано, что

сейчас появился более обоснованный метод построения мо-