Лукашин Ю.П. Адаптивные методы краткосрочного прогнозирования временных рядов

Подождите немного. Документ загружается.

Таблица

2.1

Значения

символов

обобщающей

формулы

Характер

сезонности

Тенденция ^"Ч.

роста

Отсутствие

тенденции

роста

Аддитивный

рост

Экспоненци-

альный

рост

Отсутствие

сезон-

ного эффекта

«M-l

ai,t~i ft-x

Аддитивный

се-

зонный

эффект

Xt—gt-l

xt—gt-l

ei,«-l+ß2,t-X

xt—gt-l

<ti,t-\

4-х

Мультипликатив-

ный

сезонный

эффект

Xtlft-l

i,t-x

xt/ft-i

01,<-1

в2,<-1

xtltt-l

«i.<-i U-x

«2, t—коэффициент линейного роста, оценивается

по

фор-

муле

—

коэффициент экспоненциального роста,

его

полу-

чают

по

формуле

—

аддитивная сезонная компонента, вычисляется

по

формуле

—

периодичность сезонного явления;

—

мультипликативный коэффициент сезонности,

подсчитывается

по

формуле

Прогнозы

фактических значений, ожидаемых

момент

т,

могут

быть получены по общей формуле

где

подсчитывается для каждой модели

способом,

указан-

ным

табл.

2.2

Таблица

2.2

Формулы

для прогнозов

V*. Характер

\. сезонности

Тенденция

>».

роста

Отсутствие

тенденции

роста

Аддитивный

рост

Экспонен-

циальный

рост

Отсутствие

сезонного

эффекта

Аддитивный се-

зонный

эффект

Мультипликатив-

ный

сезонный

эффект

АППРОКСИМАЦИЯ

ПОЛИНОМИАЛЬНЫХ

ТРЕНДОВ

С ПОМОЩЬЮ

МНОГОКРАТНОГО

СГЛАЖИВАНИЯ

Многократное сглаживание

В главе

было рассмотрено экспоненциальное

сглаживание для оценки текущего значения единственного

коэффициента

прогнозной модели;

мы

познакомились

одно-,

двух-

трехпараметрическими моделями линейного

роста. Наиболее предпочтительной оказалась однопарамет-

рическая модель Брауна, отличающаяся рядом достоинств.

Р.

Г.

Брауном и Р. Ф. Майером [481 эта модель была разви-

та

для

более сложных процессов путем включения

в нее

большего количества полиномиальных

членов.

Оценка

коэф-

фициентов

полиномиальных членов производится путем

многократного сглаживания. Здесь также предполагается,

что значения коэффициентов

будут

меняться медленно и

оценки

этих величин

будут

основываться на последних

наблюдениях х

#,_!, ..."

Понятие

экспоненциальной средней S

для временного

ряда x

можно обобщить на случай экспоненциальных сред-

них более высоких порядков. Экспоненциальная средняя

произвольного /7-го порядка определяется как

начальные значения экспоненциальных средних соответ-

ствующего

порядка, т. е. выравнивание р-го порядка явля-

ется простым экспоненциальным сглаживанием, применен-

ным

к результатам сглаживания (р — 1)-го порядка.

Если в качестве гипотезы тренда некоторого процесса

•принимается полином степени п, то метод

экспоненциального

сглаживания и прогнозирования позволяет вычислить ко-

эффициенты

предсказывающего полинома через экспонен-

циальные средние соответствующих порядков.

В общем

случае

принимается гипотеза, что исследуемый

процесс является параболой /г-го порядка, а прогноз на т

шагов вперед выражается формулой

где параметры Ъ

, ..., а

п + 1

нужно определить.

Идея

экспоненциального предсказания основана на том,

что прогноз осуществляется полиномом, представляющим

первые п + 1 членов разложения процесса x

в ряд Тейло-

ра:

Если наблюдаемый процесс может быть представлен по-

линомом степени я, то все производные порядка я + 1 и

выше

будут

равны нулю.

, Фундаментальная теорема метода экспоненциального

сглаживания и прогнозирования, впервые доказанная

> Брауном и Р. Майером [48], говорит о том, что

коэффи-

циенты а

, а

, .... а

п + х

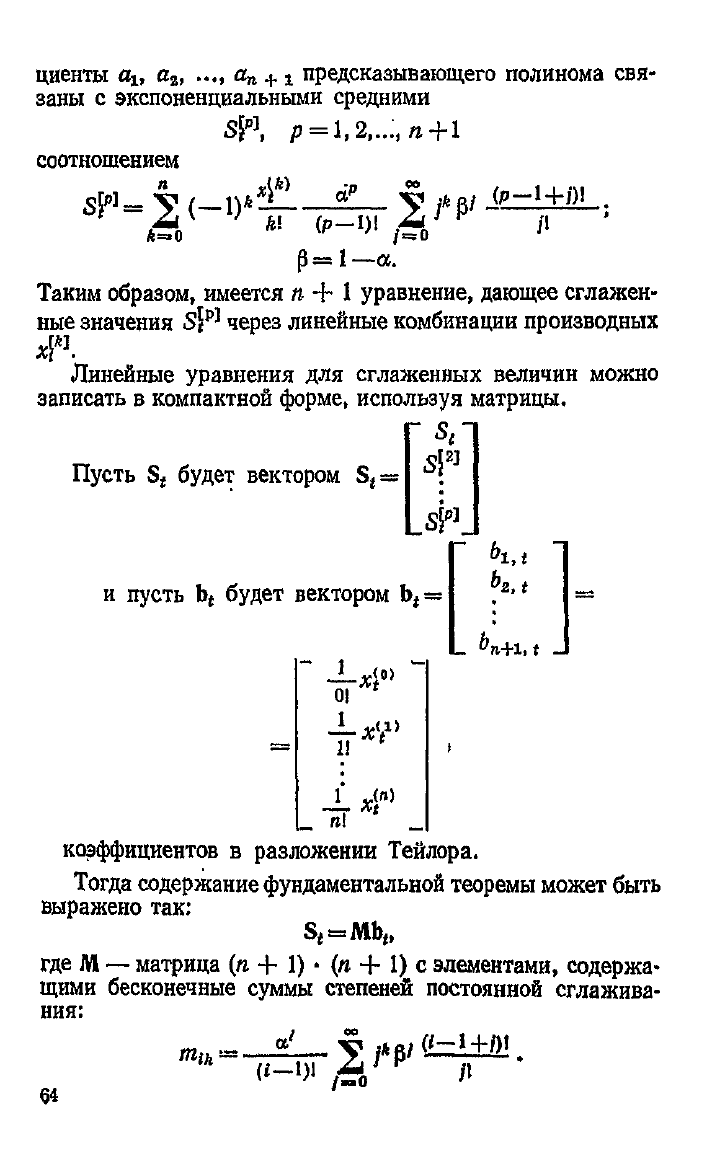
предсказывающего полинома свя-

заны

с экспоненциальными средними

соотношением

Таким

образом, имеется п + 1 уравнение, дающее сглажен-

ные

значения Sj

через линейные комбинации производных

х?\

Линейные уравнения для сглаженных величин можно

записать в компактной форме, используя матрицы.

коэффициентов

в разложении Тейлора.

Тогда содержание фундаментальной теоремы может быть

выражено так:

где

— матрица (п + 1)

•

(п

•+•

1) с элементами, содержа-

щими

бесконечные суммы степеней постоянной сглажива-

ния:

Система« +

линейных уравнений может

быть

разреше-

на

относительна

коэффициентов

предсказывающего полино-

ма по формуле

Для экстраполяции трендов обычно используются поли-

номы

не выше второго порядка. Для этих

случаев

элементы

обратной матрицы М"

определяются аналитически как

функции

постоянной сглаживания а.

Д.А.Д'

Эзопо-

[58] доказал, что для любой последова-

тельности наблюдений полином Р степени п, полученный с

помощью многократного сглаживания, является решением,

которое минимизирует взвешенную

сумму

квадратов оши-

бок:

Экспоненциальное

сглаживание очень просто. Однако

надо отметить, что для сглаженных величин Sp

]

, p — 1,2,

.-., п + 1 должны быть установлены начальные значения.

Простейший

путь

задания исходных условий — оценка ко-

эффициентов

полинома разложения.

Если

имеются выборочные данные, то эти оценки

могут

быть получены методом наименьших квадратов,

как

это

де-

лается в регрессионном анализе. Для новых временных ря-

дов

коэффициенты

должны быть предсказаны или на основе

аналогии с другими подобными рядами, или исходя из ожи-

даемых

характеристик моделируемого процесса. В том и

Другом

случае

должны быть некие начальные оценки этих

коэффициентов.

При

выборе порядка

полинома

обычно решается

вопрос

том, окупается ли сложность расчетов по выбранной кри-

вой

повышением точности прогнозирования. На практике

используются полиномы не выше второго порядка. Приве-

дем формулы расчета по этим моделям.

Во

всех

рассматриваемых ниже

случаях

предполагается,

что тренд может быть представлен полиномом и наблюдает-

ся

при наличии шума, т. е.

где е

— белый шум.

-18бб

Ожидаемое значение x

в момент Т +

будем

обозна-

чать

(Т), где t — время упреждения, на которое

делается

прогноз; Т — текущий момент времени.

Адаптивная полиномиальная мо-

дель

нулевого

порядка: я = 0.

Гипотеза: % = а

Экспоненциальная средняя:

Начальное условие:

Оценка коэффициента:

Прогноз:

Адаптивная полиномиальная

модель

первого порядка: п — \.

Гипотеза: \

= ÖI + a^t.

Экспоненциальные средние:

Начальные условия:

Оценки

коэффициентов:

Прогноз:

Адаптивная полиномиальная мо-

дель

второго порядка: п = 2.

Гипотеза:

Экспоненциальные средние:

Начальные условия:

Оценка коэффициентов:

Прогноз:

Итак,

прогнозы являются линейными комбинациями вы-

равненных величин. Целью выравнивания данных явля-

ется получение рекурсивных процедур пересмотра перво-

начальных оценок коэффициентов полинома.

Свойства полиномиальных моделей

Многократное экспоненциальное сглаживание является

линейной

дискретной системой с постоянными коэффициен-

тами и может быть поэтому полностью описано своей реак-

цией

на импульс. Изучив реакцию на импульс, легко полу-

чить реакции на

другие

стандартные входные потоки.

Раньше

мы рассмотрели реакцию на импульс системы од-,

нократного экспоненциального сглаживания и использова-

ли ее для изучения динамических свойств модели. Это было

полезно для практического выбора компромиссного значе-

ния

константы сглаживания а.

Можно

провести подобный же анализ для системы много-

кратного сглаживания. Для этого вводят понятие эквива-

лентной постоянной сглаживания, которое позволяет вы-

воды, сделанные для однократного экспоненциального сгла-

живания,

распространить на случай сглаживания любого

порядка.

Предположим, что достаточно долго входной поток х =

экспоненциальные средние

всех

порядков также равны

нулю. Затем в момент времени t — 0 на

вход

подается еди-

ничный

скачок х

— 1. Это может быть импульс, ступенча-

тое изменение или начало какой-либо

другой

временной

функции.

Экспоненциальная средняя первого порядка при-

мет значение а: Реакция экспоненциальной средней второ-

го порядка

будет

, Реакция экспоненциальной средней

k-то

порядка

будет

. На основании фундаментальной тео-

ремы оценка свободного члена

Xtt

для полиномиальной

модели л-порядка

тогда

будет

выражена так:

Для анализа моделей, использующих экспоненциальные

средние высокого порядка, удобно определить эквивалент-

ную постоянную сглаживания таким образом, чтобы оценки

свободного члена для различных моделей были одинаковы-

ми.

Пусть при однократном выравнивании использовалась

постоянная

сглаживания а

. Тогда для модели линейного

роста, использующей двойное сглаживание, значение эк-

вивалентной постоянной а

будет

такое, что

Вообще для выравнивания порядка р эквивалентная по-

стоянная

сглаживания

будет

такая, что

Это определение эквивалентной постоянной связано так-

же с другой эквивалентностью. Для любой полиномиальной

модели свободный член a

lt t

может быть оценен рекурсивно:

где х

(t—l) — ожидаемое значение наблюдения в момент

t, полученное на основе информации, имевшейся к моменту

t—l,

Следовательно, эквивалентная постоянная сглаживания

дает

одинаковую коррекцию свободного члена при одинако-

вой ошибке прогноза на 1 шаг вперед.

Реакция

адаптивных полиноми-

альных моделей нулевого, первого и

второго порядков. На рис. 2.3, 2.4, 2.5, 2.6 адап-

тивные полиномиальные модели нулевого, первого и второ-

го порядков с эквивалентными постоянными сглаживания

сравниваются по их реакции на импульс, на ступенчатое

изменение уровня, на входной поток с линейным ростом, на

параболу при периоде упреждения т« 3. Наиболее сильно

на

импульс реагирует полиномиальная модель второго по-

рядка (см. рис. 2.3). „ „ „.„

На

рис. 2.4 видно, что прогноз на три шага вперед в кон-

це концов стремится к уровню ступенчатого изменения, но

более сложные модели

требуют

на это больше времени, ре-

акция

может быть ускорена увеличением постоянной сгла-

живания,

, ,

ЛЙ

.,__„

Стоит отметить, что прогнозы по полиномиальной моде

ли первого порядка превышают уровень ступенчатогоскач

ка

и стремятся к нему

сверху,

в то время как прогнозы по

квадратической модели превышают новый уровень входно

го потока, затем опускаются ниже и стремятся к нему сни

'Рис.

2.5 показывает, что после первоначального переход-

ного периода прогнозы полиномиальной модели нулевого

порядка отстают от линейно растущего входного-потока на

постоянную величину; прогнозы полиномиальной модели

первого порядка в конце концов приближаются к деистви

тельным значениям ряда; прогнозы полиномиальной моде

ОУ

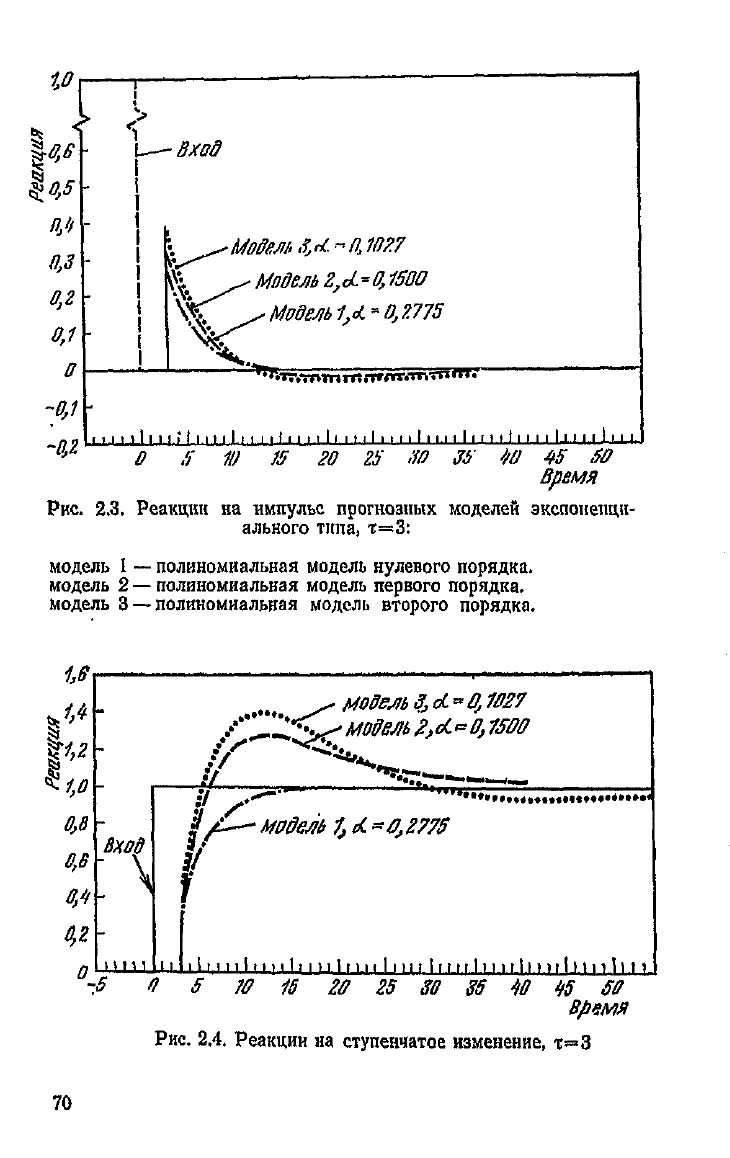
Рис.

2.3. Реакции на импульс прогнозных моделей экспоненци-

ального типа, т=3:

модель

— полиномиальная модель нулевого порядка,

модель 2 — полиномиальная модель первого порядка,

модель

—полиномиальная модель второго порядка.

Рис.

2.4. Реакции на ступенчатое изменение, х~3