Лукашин Ю.П. Адаптивные методы краткосрочного прогнозирования временных рядов

Подождите немного. Документ загружается.

— неавтокоррелированный шум с нулевым математи-

ческим

ожиданием.

Адаптивная модель с мультипликативной сезонностью

была предложена

П.

Р. Уинтерсом [113]. Аддитивная модель

рассмотрена Г. Тейлом и С. Вейджем [103].

Уинтерс поставил

задачу

разработать модель для прогно-

зирования

объемов сезонных продаж

использованием

ЭВМ.

Модель должна быть

такой,

чтобы: а) прогнозы рассчиты-

вались на основе одних

тех же программ для большого ко-

личества продуктов; б) вычисления производились быстро

дешево; в) использовался минимальный объем памяти

для информации; г) учитывались изменяющиеся условия.

Прогнозы

объемов продаж предназначаются для систем

управления запасами и планирования производства. Такие

системы предполагают наличие правил принятия решений,

которые определяют, когда и сколько производить или за-

казывать отдельных видов товаров. Правила однообразно

применяются

ко многим продуктам, часто к десяткам ты-

сяч

или

даже

сотням тысяч изделий. Прогнозы должны де-

латься часто (ежемесячно или еженедельно). Метод прогно-

зирования

должен быть четко формализован, что необходи-

мо для автоматической обработки на ЭВМ. Необходимо

иметь возможность легко вводить

свежую

информацию о

фактических продажах.

Для прогнозирования продаж отдельных видов товаров

могут

быть применены несколько методов. Модель Уинтер-

са базируется на анализе изолированных временных рядов

продажах. Единственной используемой информацией яв-

ляется предыстория продаж данного товара.- Модель Уин-

терса является моделью экспоненциального типа. Эта схе-

ма, очевидно, имеет необходимые характеристики.

Для некоторых продуктов, характеризующихся стабиль-

ной

интенсивностью продаж и малыми сезонными колеба-

ниями,

уже простая экспоненциальная модель является

вполне удовлетворительной.

Многие

продукты,

однако,

име-

ют заметную тенденцию роста или падения продаж, осо-

бенно

когда они производятся впервые или когда появля-

ются конкурирующие товары. Для некоторых продуктов

существенны сезонные изменения уровня продаж.

Поэтому

целесообразно в прогностических моделях учи-

тывать конкретный характер тенденции и сезонных колеба-

ний.

Это и

сделал

Уинтерс с помощью экспоненциальной

схемы. Модель

при

этом

становится сложнее, зато

точность

прогнозов для большинства товаров существенно возраста-

ет.

Прежде чем переходить к полной модели Уинтерса, от-

ражающей и сезонность, и линейную тенденцию роста, рас-'

смотрим более простой вариант, который содержит только

сезонный эффект.

Прогнозирование с коэффициентами сезонности

Модель имеет вид:

Как

видим, a

lt t

является взвешенной суммой текущей

оценки

т^—,

полученной

путем

очищения от сезонных коле-

баний фактических данных x

и предыдущей оценки

ltt

_!•

В качестве коэффициента сезонности Д берется его наиаолее

поздняя оценка, сделанная для аналогичной фазы цикла.

Затем величина a

ti t

, полученная по первому уравнению, ис-

пользуется для определения новой оценки коэффициента

сезонности по второму уравнению.

Прогноз

следующего

значения ряда:

Более общим выражением для прогноза на х шагов впе-

ред

будет:

Величины

v.f

могут

быть записаны через прошлые

данные и начальные условия:

Если прогнозы составляются на отрезок времени, больший чем

I, то повторно используется / наиболее свежи* оценок коэффициен-

тов сезонности Ъ

t-i, ,..,%

где a

— начальное значение а

— начальное значение f в соответствующей i фазе

(месяце)

цикла (года);

J — наибольшая целая часть

Следовательно, прогноз является функцией всех прош-

лых значений фактического ряда, параметров а

и а

и на-

чальных условий 2^,0, fi,

, ?i.o, -, ho-

Влияние

начальных условий на прогноз зависит от ве-

личины

весов и длины ряда, предшествующего текущему

моменту t. Влияние ai,

обычно

будет

уменьшаться быстрее,

чем влияние начальных

значений

, так как а

пересмат-

ривается на каждом шаге, а ft только один раз за цикл.

, Если эта сезонная модель прогнозирования, структура

которой

не содержит элементов для отражения какой-либо

тенденции

роста, применяется для прогнозирования ряда,

•характеризующегося ярко выраженной тенденцией, то ко-

эффициенты

% перестают быть простыми коэффициентами

сезонности

и вскоре вбирают в себя в определенной мере

эффект

роста.,

Например,

при обработке ряда ежемесячных

наблюдений с длительной тенденцией к повышению

будет

получена сумма двенадцати /ь превышающая 12. Именно

это

и компенсирует отсутствие в

структуре

модели соответ-

ствующих элементов.

Если

ряд имеет

тенденцию,

а многие

ряды,

по-видимому,

ее имеют, то в модель необходимо ввести специфический

член,

учитывающий эту тенденцию.

Модель

сезонных

явлений

линейным

ростом

Полная

сезонная модель Уинтерса с линейным ростом

аналогична только что рассмотренной:

Единственным изменением в выражении для a

1>t

являет-

ся

добавление а

-1 — наиболее поздней оценки аддитив-

ного фактора роста, характеризующего изменение среднего

за полный сезонный цикл уровня процесса за единицу вре-

мени

(месяц). Выражение для обновления коэффициента

сезонности остается тем же, что и раньше. Оценки

дифицируются по аналогичной процедуре экспоненциаль-

ного сглаживания. Прогноз является здесь функцией прош-

лых и текущих данных, параметров а

<х

, а

и первона-

чальных значений а

1)0

, я

,о>

ff,о«

Качество и точность прог-

нозов

зависит от этих факторов.

Оптимальные параметры a

Уинтерс предлагает

находить экспериментальным путем. Критерием сравнения

он

берет стандартное отклонение ошибки. При этом предпо-

лагается, что прогноз не смещен. Поиск, осуществлялся с

помощью сетки значений а

, а

. Функция стандартной

ошибки

вблизи минимума предполагалась достаточно пло-

ской.

У Уинтерса и

других

исследователей это положение на-

шло экспериментальное подтверждение. В связи с этим

предполагалось использовать один набор весов для ши-

рокого класса продуктов. Уинтерс использовал данные за

5—7 лет. При этом рядами были: данные о

продажахдсухон-

ной

утвари, о продажах краски, о котлованах для изготов-

ленных заводским способом сооружений. Первая часть рядов

(2—3

года)

использовалась для построения модели, а на ос-

тальных данных проверялась точность прогнозирования.

Для получения представления о влиянии различных на-

боров величин (a

, а

) на все три ряда сразу Уинтерс

предложил

следующую

комбинированную оценку. В каче-

стве меры потерь в точности прогнозирования для каждого

ряда в отдельности при данном наборе (a

, a

, а

) он брал

возрастание дисперсии ошибки, выраженное в процентах,

по

сравнению с дисперсией, соответствующей оптимальным

параметрам сглаживания. Например, при (0,2; 0,4; 0.,2)

для первого ряда превышение над минимумом составило

2л>, для второго — 2%, а для

третьего

— 22%. Комбини-

рованная

оценка равна их сумме —26%. Наилучшей ком-

бинированной

оценкой у Уинтерса были 24% при (0,2;

и,4; 0,1),

Определение оптимальных параметров путем минимиза-

ции

комбинированной оценки является попыткой найти

универсальные веса, подходящие для широкого класса ря-

дов. Несмотря на то что полученный результат несет отпе-

чаток специфических свойств использованных рядов, он

является полезным ориентиром при работе с недостаточной

информацией.

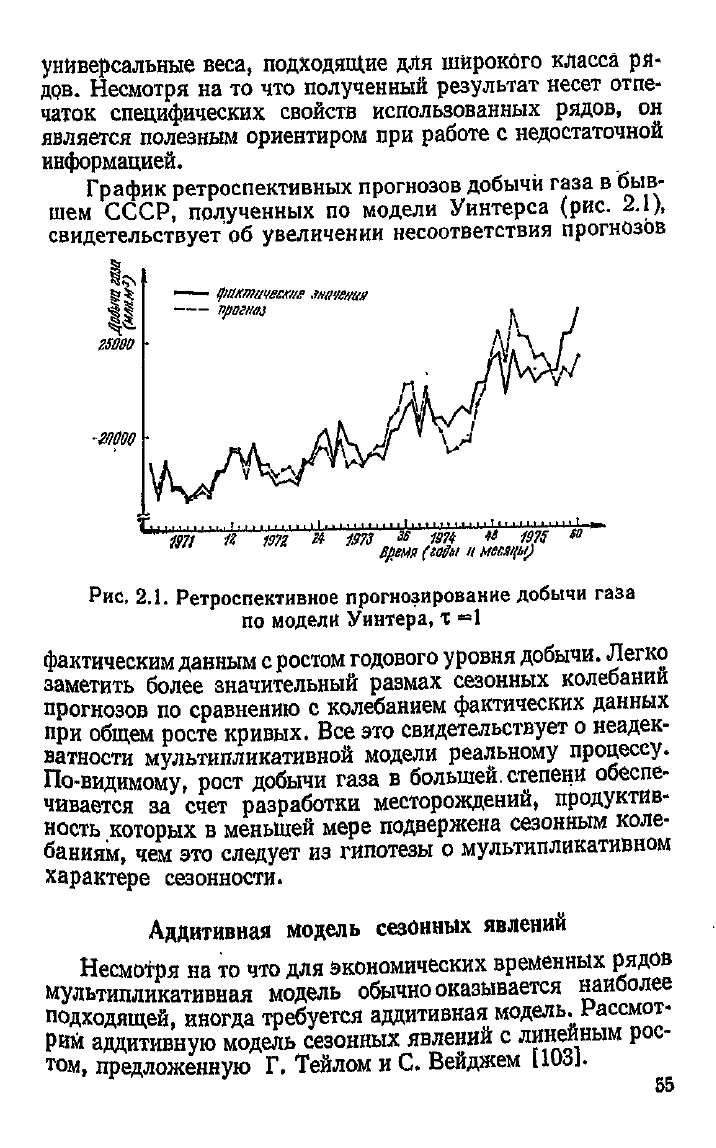
График

ретроспективных прогнозов добычи газа в быв-

шем

СССР,

полученных по модели Уинтерса (рис. 2.1),

свидетельствует об увеличении несоответствия прогнозов

Рис,

2.1. Ретроспективное прогнозирование добычи газа

по

модели Уинтера, т =1

фактическим

данным

ростом

годового уровня

добычи.

Легко

заметить более значительный размах сезонных колебании

прогнозов

по сравнению с колебанием фактических данных

при

общем росте кривых. Все это свидетельствует о неадек-

ватности мультипликативной модели реальному процессу.

По-видимому, рост добычи газа в

большей,

степени

обеспе-

чивается за счет разработки месторождений, продуктив-

ность которых в меньшей мере подвержена сезонным коле-

баниям,

чем это

следует

из гипотезы о мультипликативном

характере сезонности.

Аддитивная модель сезонных явлений

Несмотря

на то что для экономических временных рядов

мультипликативная модель

обычно

оказывается

наиболее

подходящей, иногда требуется аддитивная модель Рассмот-

рим

аддитивную модель сезонных явлений с линейным рос-

том, предложенную Г. Тейлом и С. Вейджем [103].

Построение такой модели имеет целью упрощение про-

цедуры

прогнозирования, поскольку комбинация мультип-

ликативной сезонной модели с линейным ростом математи-

чески громоздка. Кроме того, на практике чаще встречают-

ся

экспоненциальные тенденции, чем линейные. Поэтому

замена значений первоначального временного ряда их ло-

гарифмами преобразует экспоненциальную тенденцию в

линейную и одновременно мультипликативную сезонную

модель в аддитивную. Тогда временной ряд (исходный или

преобразованный)

можно представить следующим образом:

(2.1)

(2.2)

rp£a

Xit

— величина уровня процесса после элиминирова-

ния

сезонных колебаний;

it t

— аддитивный коэффициент роста;

— аддитивный коэффициент сезонности;

— белый шум.

Сначала рассмотрим адаптивную процедуру обновления

значения

1)t

момент t

мы

располагаем наблюдением x

, о

котором известно, что

Однако о

шуме

и сезонном факторе g

никакой информации

нет. Величину e

заменим нулем, а в качестве заменителя

для g

возьмем

самую

последнюю оценку сезонного фактора

.i,

где / — период сезонного цикла.

Величину

Xf—gt-t

будем

рассматривать как новое

«фактическое» значение a

t) t

. Последней оценкой уровня

а%

является äi

t t

но она

соответствует

моменту t—l, а не t.

Поэтому необходимо к

Oj.i-i

добавить ещеа

2(<

(см.2.2).

Но

так как оценку а

мы

еще

не

можем получить, то вместо

нее берем оценку a

%t t

полученную на предыдущем шаге.

Это приводит к следующей процедуре адаптации:

(2.3)

которая

при

данных

весах

— а

) оценивает а

1( t

через

наиболее свежее наблюдение

ранее подсчитанные

величи-

Об особенностях прогнозирования временных рядов после

логарифмического преобразования см. приложение № 3.

Учитывая (2.2) и вычитая из полученного ä

lt t

прежнюю

оценку«^

_i, можем получить оценку ä

Zt t

. Однако посколь-

ку вычисления *£,

не

являются совершенными, в частности

потому, что не принимались в расчет остатки из (2.1), то,

очевидно,

лучше

не полагаться на эту разность полностью,

а считать ее «фактическим» свидетельством динамики ряда

объединить со старым значением

,t-i

по

известной

формуле экспоненциального сглаживания

(2-4)

где а

и (1 — а

) — веса

двух

источников информации.

Наконец,

та же процедура применяется для получения

оценки

. Новое «фактическое» значение сезонного фактора

будет

— а

Ху ь

старое значение равно g

экспоненци-

ально-сглаженное значение

(2.5)

Все три параметра • сглаживания

будут

удовлетворять

условию 0 <; <х

, а

<С

Адаптивное прогнозирование теперь провести сравни-

тельно просто. Предположим, что t — текущий момент вре-

мени,

так что d

,t, «a.t

gt>

St-if

— имеются в нашем рас-

поряжении.

Предположим также, что мы хотим получить

прогноз величины

Xt+%

(прогноз на % шагов вперед). Экст-

раполируем тенденцию линейного роста, используя самое

последнее значение коэффициента a^

, добавляем

самую

свежую

оценку сезонного члена для этой фазы цикла и пре-

небрегаем шумом. В

результате

получаем

при

условии, что 0 < t < /. Если

< х < 2/, то необходи-

мо

gf-j-и

заменить на

gt-ц+х

и т

* Д«

Модель готова, Однако на практике

удобнее

осуществ-

лять адаптивное регулирование a

lt u

с помощью

Уравнений, связывающих эти величины с ошибкой прогно-

за, сделанного в конце периода t — 1 на один шаг вперед.

Уравнение (2.3) можно переписать следующим образом:

из

уравнений (2.3)

—

(2.5) легко получить:

(2.7)

(2.8)

Корректировки

всех

параметров модели совпадают

по

знаку

пропорциональны по величине ошибке последнего

прогноза

на

один

шаг

вперед. Коэффициентами пропорци-

ональности

будут а

сс

—

ai)a

соответственно.

Можно заметить,

что

процедура (2.3)

—

(2.5) является

рекурсивной

том смысле,

что

для определения

lt t

исполь-

зуются прошлые данные

сезонных колебаниях

коэффи-

циенте роста. Оценка %,

используется

для

получения но-

вых значений а

Но совершенно очевидно,

что

прош-

лые значения сезонного фактора

коэффициента роста

при

вычислении

1г

являются лишь суррогатом;

не

лучше

ли

было использовать более свежие, текущие

оценки

этих ком-

понент? Рассмотрим такой вариант.

Вместо выражения (2.3) имеем:

(2.9)

Выражения (2.4)

(2.5) остаются прежними, и

путем

их

под-

становки

в (2.9)

получаем:

При

этом 0<а{-<1. Общая форма выражения,

как

видим,

та же, что и в

(2.3).

выражениях (2.6),

(2.7) и

(2.8) лишь

меняется на

а{, в

остальном они остаются

без

изменений.

Отметим, что

а! =

при

» а

Альтернативы моделей

Вообще возможно множество комбинаций различных

типов

тенденций и циклических явлений аддитивного и

мультипликативного вида. В работе [93] представлены де-

вять возможных моделей, которые обобщенно выражены

одной

формулой. Поскольку

всегда

необходимо использо-

вать модель, наиболее точно отражающую динамику про-

цесса, то целесообразно остановиться на этом вопросе под-

робнее.

Девять упомянутых моделей составляют три группы по

три варианта в каждой. Графическое отображение первой

группы представлено на рис. 2.2, а. Ее

образуют

модель

без тренда

—А, модель с аддитивным линейным трен-

дом 1 — В и модель с мультипликативным (экспоненциаль-

ным)

трендом 1—С.

Вторую

группу

(рис. 2.2, б) составляют

три модели из первой группы с наложенным на них аддитив-

ным

сезонным'эффектом. В

третью

группу

(рис.

2.2,б)

входят

три модели из первой группы, но с наложенным на

них мультипликативным сезонным эффектом.

Из

девяти моделей большинство представляются прак-

тически полезными и лишь модель 3—Л, по-видимому, не-

реалистична. Графики на рис. 2.2 позволяют быстро выб-

рать в конкретном

случае

наиболее

подходящую

модель по

имеющимся

прошлым данным или на основе предположе-

ний

будущем

поведении ряда.

Все девять моделей

могут

быть отражены в одной общей

записи

где а

1( t

— текущий уровень ряда после элиминирования

сезонных колебаний;

— параметр сглаживания, 0 < а

< 1;

значения

даны в табл.

2.1,

каждая клетка которой

характеризует ту или иную модель.

Например,

модель В—2

аддитивным трендом

аддитив-

ным

сезонным эффектом записана в клетке, находящейся

на

пересечении строки В и колонки 2.

Рассмотрим величины, соответствующие в обобщенной

формуле символам 4 и 4

— фактическое наблюдение;