Лукашин Ю.П. Адаптивные методы краткосрочного прогнозирования временных рядов

Подождите немного. Документ загружается.

Реакция

на ступенчатое изменение

При

наличии существенных долговременных изменений

структуры

ряда необходимо добиваться, чтобы модель учи-

тывала их как можно быстрее. Рассмотрим прежде всего

ступенчатое изменение уровня входного потока. Запишем

его аналитически:

В экономических исследо-

ваниях ступенчатое измене-

ние

может отражать резкое

изменение уровня производ-

ства, спроса или потребле-

ния

какого-либо товара в ре-

зультате

поворота

моды,

внед-

рения

значительного науч-

ного открытия, изменения

политической или внешнеэко-

номической ситуации.

Единичный

ступенчатый скачок является следующей

функцией:

Так

как рассматриваемая процедура сглаживания-явля-

ется

линейной,

то

можно

определить

реакцию

на такого рода

изменения

с помощью реакции на единичный' импульс.

Реакция

модели

будет

Рис.

1.5.

Влияние

а на

скорость

реакции

прогнозной

модели

при

т=3

ростом t член ß'+i становится незначительным и ве-

личина S

приближается к уровню x

На

рис. 1.5 показана реакция модели экспоненциальной

•средней на ступенчатый скачок при различных значениях

постоянной'

сглаживания (т — 3). Здесь, как видим, для

скорейшего отражения произошедших изменений выгоднее

брать большее значение с*.

Реакция

на линейную.и квадратическую функции

Временные экономические ряды часто имеют тенденцию

линейного или параболического роста. Можно показать,

что при линейно-нарастающем входном потоке а

+ a

t экс-

поненциальная

средняя

будет

постоянно отставать от вре-

менного ряда и что это отставание в конце концов стремится

величине - а

, т. е. чем больше а, тем меньше отставание.

При

квадратическом входном потоке типа a

+ a

t 4-

сф экспоненциальная средняя отстает от временного

ряда все больше и больше. Наименьшее отставание

будет

при

а«1.

При

прогнозировании в этих обоих случаях нельзя от

модели экспоненциальной средней ожидать хороших прог-

нозов.

Для таких временных рядов требуются

другие

модели,

которые мы рассмотрим ниже.

В сводной табл. 1.8 приведены реакции экспонен-

циальной средней на рассмотренные входные потоки.

Таблица 1.8

Реакции

экспоненциальной сродней

на

стандартные входные потоки

ВХОДНОЙ

ЛОТОК

Импульс

xt = 6(t)

Ступенчатый

скачок

„ Г(Н<0,

*<-{i />о

Линейный

рост

Ы, feß

Парабола

*=>t

Q>0

Экспоненциал ьная

средняя

aß'

l-ß'+

Установившаяся

ошибка

Xfjc—Sco

•

Приведенные

реакции

простейшей

модели

на

входные

ряды,

представляющие

типичные

нарушения

стационар-

ности,

говорят

противоречивых

требованиях

постоян-

ной

сглаживания в задаче

прогнозирования.

Это свидетель-

ствует

о существовании оптимального значения а,-которое

зависит от того, какой тип изменений в процессе встречает-

ся

наиболее часто. Кроме того, из табл. 1.8

следует,

что

даже

когда адаптивная модель становится неадекватной

исследуемому ряду, она все же в какой-то мере учитывает

реальные

изменения,

хотя в этом

случае

лучше всего заме-

нить

модель.

Реакция

на синусоидальную волну

Во многих случаях временные ряды по.своей природе

являются

периодическими.

Браун

показал,

что реакция

экс-

поненциальной

средней на входной поток x

— sin ~

будет:

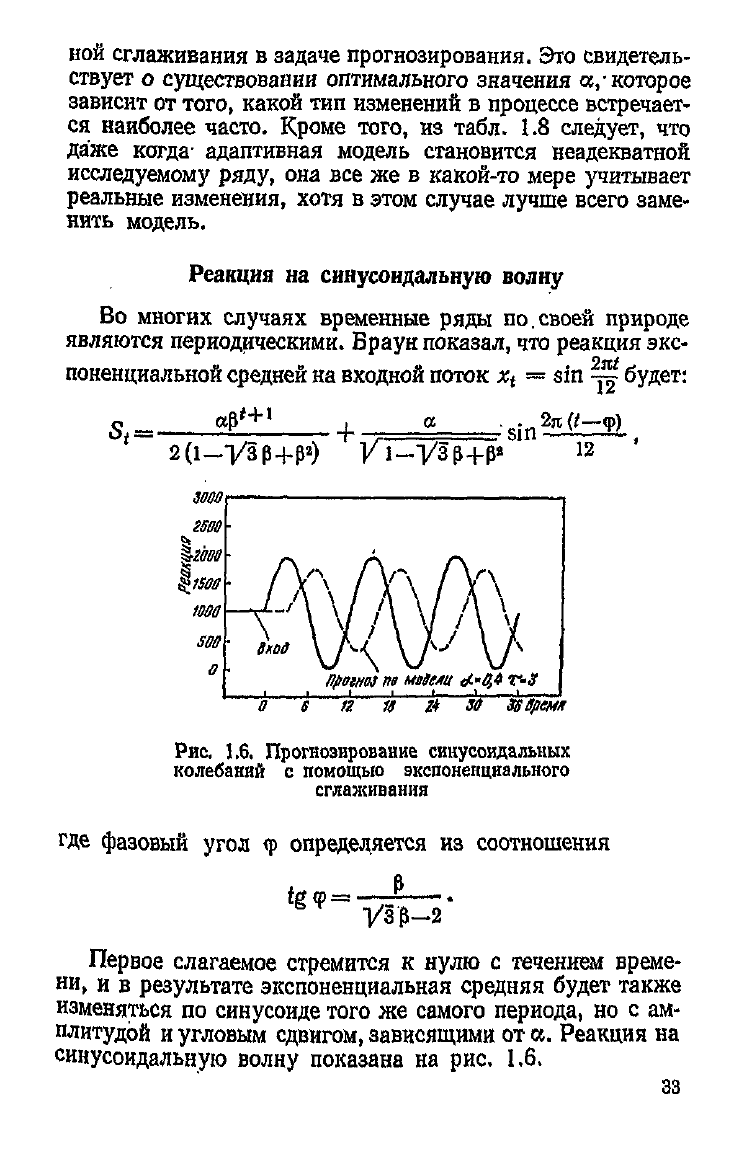
Рис.

1.6. Прогнозирование синусоидальных

колебаний

с помощью экспоненциального

сглаживания

где фазовый

угол

ф определяется из соотношения

Первое

слагаемое стремится к нулю с течением време-

ни,

и в результате экспоненциальная средняя

будет

также

изменяться

по синусоиде того же самого периода, но с ам-

плитудой

угловым сдвигом, зависящими от а. Реакция на

синусоидальную волну показана на рис. 1.6.

При

определенных значениях

ряд

его прогно-

зы

по экспоненциальной средней

могут

оказаться колеблю-

щимися

противофазе, что приведет кочень большим ошиб-

кам.

Как предиктор синусоидальных процессов данная мо-

дель совершенно неудовлетворительна.

§ 6. СВОЙСТВО ОПТИМАЛЬНОСТИ

Главное достоинство прогнозной модели, осно-

ванной

на

экспоненциальной средней, которре мы устано-

вили,

состоит

том, что она способна последовательно адап-

тироваться

новому уровню процесса

без

значительного

реагирования

на

случайные отклонения. Однако целесооб-

разно

определить статистические свойства таких временных

рядов,

по

которым этот метод прогнозирования рабо-

тает

особенно хорошо.

результате

можно

будет

лучше

судить

сфере применения этого метода или модифициро-

вать его в том случае, когда необходимые свойства

времен-

ного ряда

отсутствуют.

Первым

этот вопрос исследовал

Д.

Мат [84].

Он

взял

временной

ряд х, генерированный математической моделью

(Ь8)

где

—

случайные независимые отклонения

со

средним

значением

0 и

дисперсией

<г|;

—

величина, получающая

на

каждом шаге некото-

рые приращения

т. е.

где величины

независимы, имеют среднее значение

0 и

дисперсию а%.

Значения

величин

ей«

пока предполагаются независи-

мыми.

Такой временной ряд можно рассматривать как слу-

чайное движение уровня процесса

%, на

которое наложен

шум

Д.

Мат

поставил

задачу

отыскать оптимальные веса

a>Ä

предикторе вида

(1.9)

которые минимизируют дисперсию ошибки прогноза ряда

(1.8). Он пришел к выводу, что оптимальными весами в мо-

дели (1.9)

будут:

Веса имеют ту же самую форму, что и в модели экспо-

ненциальной

средней, определяемой выражением

если положить а = 1 —

К.

Следовательно, модель экспо*

ненциальной

средней в данном

случае

является оптималь-

ной

при

Если дисперсия приращений уровня аЦ мала по срав-

нению

с дисперсией шума о|, то а

будет

близка к 0. Прог-

нозы

в таком

случае

мало зависят от новой информации.

Низкое

значение а обеспечивает хорошую фильтрацию шу

ма. И наоборот, если ol велика по сравнению с дисперсией

шума, то а

будет

близка к 1, так что вес новой информации

возрастет,

В том случае, если ей« коррелированы и

необходимо только в выражении для

заменить отношение

§ 7. МОДЕЛИ ЛИНЕЙНОГО

РОСТА

В §5 было показано, что экспоненциальная

средняя приводит к смещенным прогнозам, т. е.

дает

систе-

матическую ошибку, когда временной ряд имеет тенденцию

линейного роста. Для этого случая разработано несколько

вариантов адаптивных моделей, также использующих про-

цедурУ экспоненциального сглаживания. В основе моделей

лежит гипотеза о том, что прогноз может быть получен по

уравнению

где ß

lf t

Zit

— текущие оценки коэффициентов адаптив-

ного полинома первого порядка.

Одной из первых моделей этого типа была двухпараме-

трическая модель Ч. Хольта [68], в которой оценка

коэф-

фициентов производится следующим образом:

(1.10)

где а

и а

— параметры экспоненциального сглаживания

(0 < а

< 1), которые мы также

будем

называть пара-

метрами адаптации.

Эти уравнения

могут

быть переписаны в виде:

где e

— x

—-

Хх

(t — 1) — ошибка прогноза.

Частным случаем модели Хольта является модель ли-

нейного роста Брауна:

(1.11)

где параметр ß

•—

коэффициент дисконтирования, характе-

ризующий обесценение данных наблюдения за единицу вре-

мени,

0< ß< 1.

Если модель Хольта усовершенствовать путем вклю-

чения разности ошибок, то получим полную трехпараметри-

ческую модель прогнозирования Дж. Бокса и Г. Дженкин-

са [44]:

где

, а

являются параметрами модели, 0 < а

, а

«з < 1;

t — x

—

lei

(t — 1) — ошибка прогнозирования.

На

основе практических испытаний модели на многих

экономических рядах Бокс и Дженкинс пришли к

выводу,

что включение в модель разности ошибок не является необ-

ходимым. Коэффициент сс

всегда

оказывался близким к

нулю. П. Харрисон [65] пришел к такому же заключению.

Это объясняется стохастическим характером данных, и, в

частности, тем, что корреляция ошибок в подобных слу-

чаях неустойчива.

Харрисон провел эмпирическое сравнение однопараме-

трической модели Брауна с многопараметрическими моде-

лями.

Многопараметрические модели ни в одном

случае

не

дали заметного преимущества. Поэтому на практике для

прогнозирования рядов с линейной тенденцией предпочти-

тельнее использовать более простую модель Брауна. Из

теоретического сопоставления различных моделей, прове-

денного П. Харрисоном [67]

Д. Вардом [108],

следует

ана-

логичный вывод. К положительным чертам метода Брау-

на

можно отнести следующие: логичная, ясная и легко

понимаемая'

концепция;

оптимальное значение единствен-

ного параметра можно быстро найти эмпирическим путем;

коэффициенты

модели прогнозирования оцениваются сов-

местно таким образом, чтобы уменьшить автокорреляцию

остатках. Все это

делает

модель Брауна легко примени-

мой.

Мы еще вернемся к ней в следующей главе.

СТОХАСТИЧЕСКИЙ

ПРОЦЕСС

ТЕЙЛА

ВЕЙДЖА

Г. Тейл и С. Вейдж [103] аналогично

тому,

как

это сделал Д. Мат [84] при изучении

экспоненциальной

сред-

ней,

в целях дальнейшего изучения свойств адаптивных мо-

делей предложили

применить

двухпараметрический предик-

тор

Хольта

(1.10)

для прогнозирования некоторого вероят-

ностного процесса, характеризующегося стохастическим

трендом. Они вывели выражения для определения опти-

мальных параметров адаптации, минимизирующих средний

квадрат ошибки прогнозирования.

Процесс

Тейла—Вейджа аналитически записывается как:

(1.12)

где

eh,

t — значение уровня исследуемого временного

ряда x

в момент t;

— прирост уровня

от

момента

t —

к моменту t\

, 'v

— временные последовательности с нулевым

математическим ожиданием, постоянными

дисперсиями и отсутствием ковариации, т. е.

M(p

') =

для любой пары

(t,

?).

Временной ряд x

не является стационарным и не име-

ет строго определенной автоковариационной функции.,

Однако

М.

Нерлов и С. Вейдж 189] показали, что из урав-

нений

(1.12)

следует

стационарность вторых разностей про-

цесса x

которые мы обозначим через y

(Xt—x

^~(x

^~-x

)=V

llt

+VH

r=v

где V—-разностный оператор, Vx

= x

— xt-i,

—.

V(Vx

Вторые разности имеют вполне определенную автоко-

вариационную функцию

(1.13)

где

Эти свойства

могут

быть использованы для решения во-

проса о возможности адекватного представления наблюден-

ного временного ряда процессом Тейла—Вейджа. При этом

не

следует

упускать из виду то обстоятельство, что оценки

автоковариационной функции являются довольно грубы-

ми

и коррелированными и точные равенства

(1.13)

на

практике

будут

выполняться лишь приближенно.

Схема составления прогноза в соответствии с

(1.10)

выглядит следующим образом:

(1.14)

(1.15)

Если ошибку прогноза, сделанного в момент t на

шаг впе-

ред, обозначить через e^t), то уравнения адаптации

(1.14)

(1.15)

можно записать в виде:

Ошибка прогноза:

Следовательно, ошибка прогноза является суммой

трех

компонент:

ошибки оценки уровня процесса в момент t,

ошибки

оценки прироста уровня в момент t и комбинации

случайных компонент v и е в момент t + 1.

Очевидно, что определение оптимальных а

и у эквива-

лентно определению оптимальных а

и а

. Оптимум обычно

отыскивается

путем

минимизации среднего квадрата ошиб-

ки

прогноза.

Но

когда рассматриваются нестационарные вре-

менные ряды, то в общем

случае

не очевидно, что средний

квадрат ошибок прогнозирования адаптивным методом явля-

ется величиной устойчивой, которая может быть минимизи-

рована. Используя соотношение

Нерлов и Вейдж показали, что проблема прогнозирования

+ 1

эквивалентна

задаче

прогнозирования второй раз-

ности y

t + 1

и что при ограничениях, наложенных на па-

раметры адаптации с^ и а

, ошибка прогноза является

линейной

комбинацией текущего и прошлых значений

стационарного ряда у{.

Это означает, что ошибки прогноза стационарны и их

средний квадрат вполне определенен.

результате

минимизации дисперсии ошибки прогноза

на

1 шаг вперед D

(1)

Тейл и Вейдж получили

следующие

результаты:

Для практического применения этого, однако, недоста-

точно, и нами в приложении № 1 выведено более общее вы-

ражение для дисперсии ошибки прогнозирования на х ^ 1

по

той же схеме.

Грубая

оценка соотношения дисперсий g

может быть

получена из соотношений

(1.13)

по подсчитанным автокова-

риациям

процесса y

. Уточнение g* производится экспери-

ментально методом проб на имеющемся отрезке ряда. Да-

вая значения в окрестностях

грубой

оценки, находят g

минимизирующее дисперсию ошибки D

(1).

Нерлов и Вейдж провели теоретический анализ

чувст-

вительности дисперсии ошибки прогноза D

(l) к ошибке

определении g

. Оказалось, что процентное изменение

дисперсии D

(1) пропорционально квадрату относитель-

ной

ошибки оценки g

с коэффициентом пропорциональ-

ности

Для

наиболее

реальных, малых

значений

даже

-ная

ошибка в оценке g

дает

увеличение в D

(1) менее чем на

1,5%.

Наши

эксперименты говорят о том, что несмотря на

довольно

жесткую

структуру

процесса Тейла—Вейдж.а его