Лукашин Ю.П. Адаптивные методы краткосрочного прогнозирования временных рядов

Подождите немного. Документ загружается.

можно использовать для аппроксимации некоторых реаль-

ных временных рядов. Сопоставительный анализ, проведен-

ный

в §3 гл. 7,

показывает,

что

процесс Тейла—Вейджа

занимает особое место среди моделей стохастических рядов.

§ 9.

ПРИМЕРЫ

Сравним свойства нескольких отрезков реаль-

ных временных рядов

со

свойствами стохастического про-

цесса Тейла—Вейджа и в тех

случаях,

когда они

будут

при-

близительно одинаковыми, построим предикторы и получим

прогнозы

и их

доверительные границы.

Для исследования возьмем сильно колеблющиеся ряды

курса акций фирмы ИБМ

цен

на

золото, приведенные

приложении № 4. Разобьем первый ряд

на 3

отдельных

участка

по 48

точек, второй

ряд

разделим

на 6

участ-

ков

по 60

точек

проанализируем автокорреляционную

функцию

для

вторых разностей соответствующих данных

(см.

табл.

1.9).

Таблица

1.9

Автокорреляционные функции

вторых

разностей

Ряд

Курс акций

фирмы

ИБМ

Цена

на

золото

№

участка

Лаг

-0,36

-0,32

-0,57

-0,59

-0,47

-0,62

-0,44

-0,20

-0,61

-0,05

-0,45

0,08

0,01

—0,01

0,07

-0,16

-0,40

0,08

-0,16

0,31

0,08

0,14

0,04

0,09

0,08

0,15

—0,01

0,03

—0,19

—0,03

-0,16

0,08

—0,07

—0,21

0,16

—0,15

0,04

—0,10

0,12

-0,11

—0,13

-0,06

0,13

-0,11

0,07

0,16

0,04

-0,05

0,04

—0,03

0,30

-0,01

Для рядов, описываемых процессом Тейла—Вейджа,

автокорреляционные функции вторых разностей должны

Используется

ряд

цен

на

золото

на

Лондонском рынке

на на*

чало

рабочего

дня

с 1

апреля

1971 г. по 14

сентября

1972 г.

иметь

следующие

свойства!

Поэтому при моделировании можно выдвинуть гипотезу

что участок 3 ряда курса акций и участки 1, 3, бряда цен

на

золото генерированы процессом Тейла—Вейджа.

Методом перебора для этих отрезков были найдены зна-

чения

g\ минимизирующие средний квадрат ошибки прог-

нозирования

на 1 шаг. Начальные условия для уравнений

адаптации находились по обычной линейной регрессии.

Затем каждый отрезок экстраполировался на х,— 10.

Экстраполяция

производилась по следующим моделям:

ИБМ

(рис.

1.7);

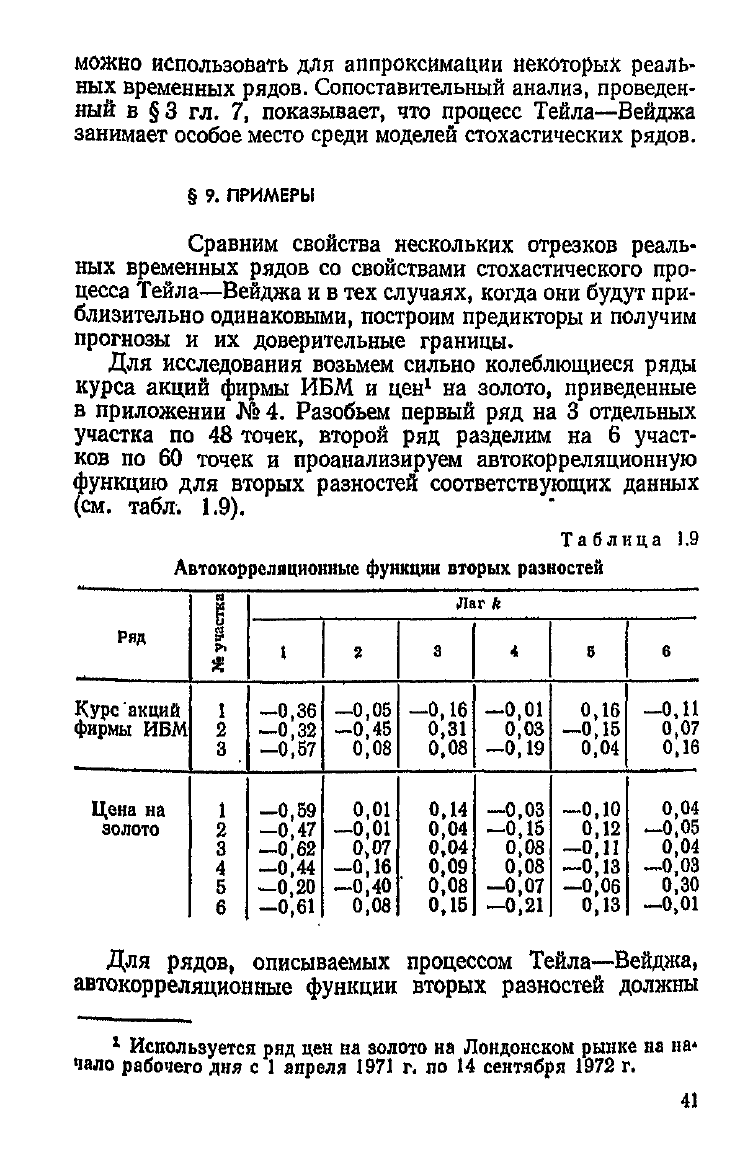
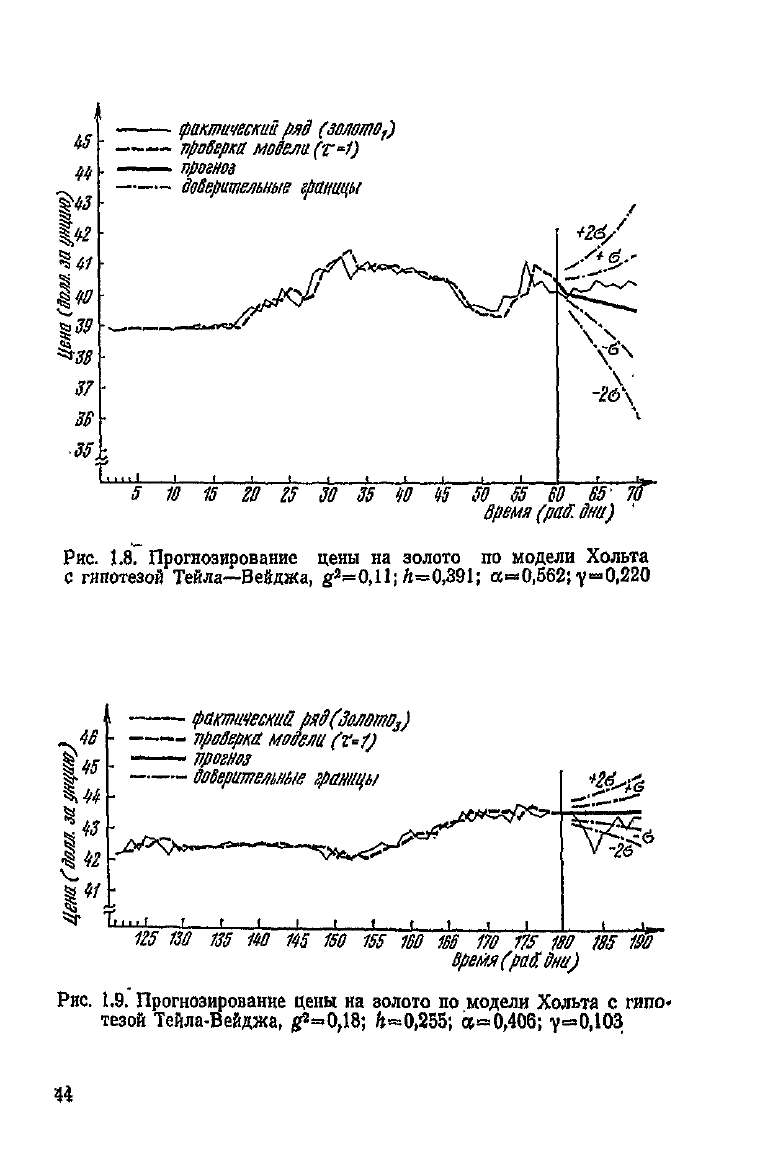
золото!(рис. 1.8);

золото

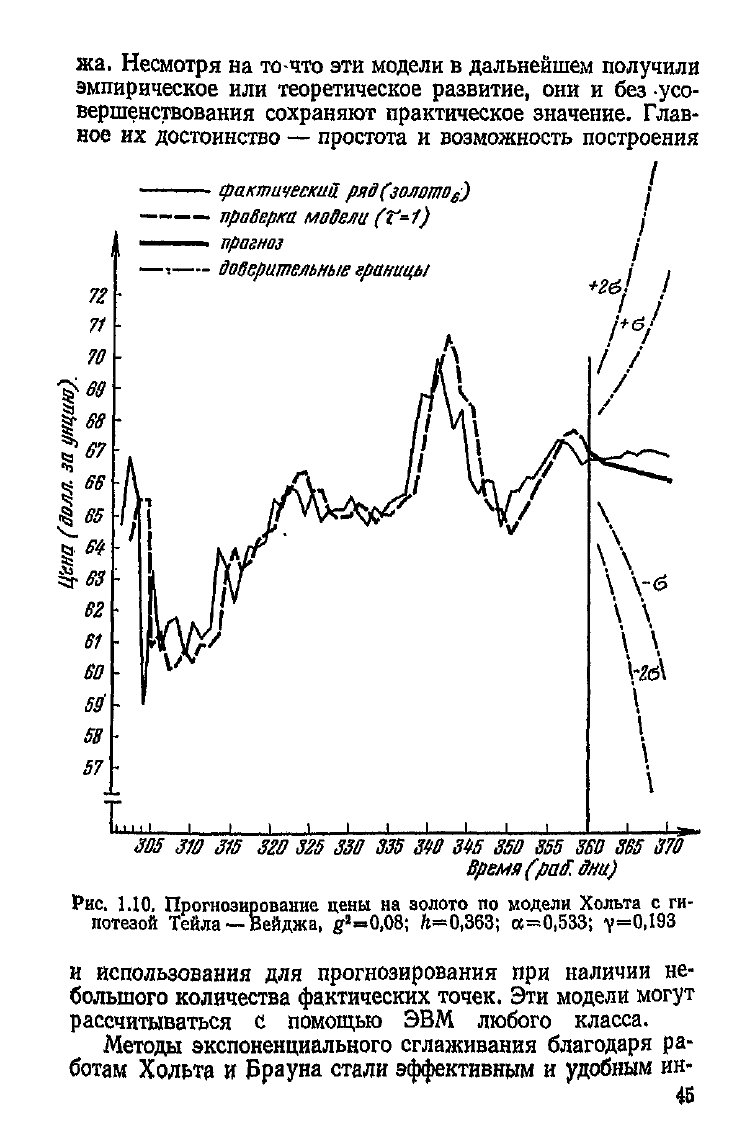
(рис. 1.9);

золото

(рис.

1.10).

Доверительные границы рассчитывались по формуле,

выведенной в приложении № 1, Результаты представлены

на

рис.

1.7—1.10.

Для отрезков

ИБМ

золото^ золото

прогнозы и до-

верительные уровни достаточно хорошо описывают

будущее

поведение процесса. При экстраполяции отрезка золото

предположении что временной ряд цен генерируется про-

цессом Тейла—Вейджа, получается слишком большой раз-

мах доверительных уровней, лишающий прогноз ценности.

Отметим, что прогнозы по адаптивной модели

могут

подсчитываться формально по одной и той же

схеме,

каким

бы ни был временной ряд. Однако качество прогноза зави-

сит от динамики процесса. Поэтому при моделировании

прежде всего делаются предположения относительно истин-

ной

структуры

ряда, выбирается наиболее подходящая мо-

дель

й в соответствии с этим рассчитываются доверитель-

ные границы полученного прогноза. Эти границы

будут

тем уже, чем

лучше

принятая гипотеза

отражает

реальные

свойства ряда. Альтернативных гипотез может быть, мно-

жество, в частности, стохастический нестационарный про-

цесс Тейла—Вейджа является одной из них.

В завершение

следует

подчеркнуть, что конечная цель

данном

случае

состояла не столько в изучении выбранных

рядов,

сколько в исследовании самого метода. Отобран-

ные

ряды характеризуются большой изменчивостью, по-

Рис.

1.7. Прогнозирование кур

са акций фирмы ™М по модели

Хольта

с гипотезой Тейла-Вейджа

=0,045;/1=0,317, а=0,482,

этому их использование для

испытания

адаптивных свойств

рассматриваемых, моделей .представляется

„

™.

К.этим

рядам

будем

обращаться и в дальнейшем. Однако

нельзя

утверждать,

что адаптивные методы являются наи-

лучшим способом прогнозирования данных рядов.

Сделаем некоторые выводы. В гл. 1 рассмотрены про:

стейшие модели экспоненциального сглаживания, линейные

адаптивные модели, стохастический процесс Тейла и веид-

Рис.

1.8. Прогнозирование цены на золото по модели Хольта

с гипотезой Тейла—Вейджа, g*«=0,ll; А=0,391;

а«0,562;у*=

0,220

Рис.

1.9. Прогнозирование цены на золото по модели Хольта с гипо-

тезой Тейла-Вейджа, £

=0,18; й=0,255; «==0,406; у=0,103

жа. Несмотря

на

то-что эти модели

дальнейшем получили

эмпирическое

или

теоретическое развитие,

они и без усо-

вершенствования сохраняют практическое значение. Глав-

ное

их

достоинство

—

простота

возможность построения

Рис.

1.10. Прогнозирование цены на золото по модели Хольта с ги-

потезой

Тейла — Вейджа, g

=»0,08; fc=0,363; а=0,533; v=0,193

использования

для

прогнозирования

при

наличии

не-

большого количества фактических точек. Эти модели

могут

рассчитываться

помощью

ЭВМ

любого класса.

Методы экспоненциального сглаживания благодаря

ра-

ботам

Хольта

Брауна стали эффективным

удобным ин-

струментом прогнозирования в экономике. В основном экс-

поненциальное

сглаживание используется для прогнози-

рования

рядов спроса и для управления ресурсами. Р. Бра-

ун [46] указывает, что благодаря этим методам прогнозиро-

вания

«в

трех

дюжинах компаний», с которыми он работал,

удалось

сократить затраты на материально-техническое

снабжение приблизительно на 150 млн. дол. при улучшении

обслуживания. С. Эйлону и Дж.

Элмалеху

[57], разработав-

шим

систему снабжения,

удалось

благодаря адаптивным

моделям уменьшить затраты на 30%. А. Моррелл, прини-

мавший

участие

в обсуждении работы Д.

Варда

[108], счи-

тает,

что экспертный прогноз спроса

дает

в среднем ошибку

40%, а метод Брауна позволяет ее уменьшить приблизи-

тельно на 30%. В работе Р. Маркланда [73] адаптивные мо-

дели используются при существенно изменяющихся усло-

виях протекания процесса и делается вывод о том, что при-

менение экспоненциального сглаживания вполне приемле-

мо для непрерывного обновления нормативной базы.

Этот метод может быть использован как для прогнози-

рования

некоторых глобальных показателей, так и в систе-

мах управления различного уровня.

Главный недостаток этих методов в том, что они рассмат-

ривают временной ряд изолированно от

других

явлений,

если

даже

имеется дополнительная информация, она мо-

жет быть использована исследователем лишь путем регули-

рования

скорости адаптации. Кроме того, точность прогно-

зов заметно падает при долгосрочном прогнозировании.

Глава 2

РАЗВИТИЕ МОДЕЛЕЙ

С ПОСТОЯННЫМИ ПАРАМЕТРАМИ

АДАПТАЦИИ

В этой

главе

рассматривается развитие лростей-

шей адаптивной модели

экспоненциального

типа

по

несколь-

ким'направлениям.

Одни

модификации

позволяют

применять

ее для изучения изменяющихся во времени законов распре-

деления вероятностей,

другие

— адекватно описывать вре-

менные ряды с лериодическими сезонными колебаниями,

третьи — аппроксимировать тенденции ряда с помощью по-

линомов с адаптивными коэффициентами.

§ 1. АДАПТИВНАЯ МОДЕЛЬ ДЛЯ ИЗУЧЕНИЯ

ЭВОЛЮЦИОНИРУЮЩИХ ЗАКОНОВ

РАСПРЕДЕЛЕНИЯ

ВЕРОЯТНОСТЕЙ

В некоторых

задачах

требуется

определить фор-

му^закона распределения вероятностей какой-либо случай-

ной

переменной, в то время как стохастический процесс,

который она представляет, претерпевает некоторые измене-

ния.

В этом

случае

нужно найти способ изучения эволюци-

онирующих законов распределения вероятностей.

Будем рассматривать полную систему п несовместных

событий, определенных на числовой оси с помощью п + 1

границы:

Если исследуются объемы заказов покупателей на ка-

кой-либо продукт, то

могут

быть, например,-определены

три события:

объем заказа менее 5 штук; 2) объем заказа

не

менее 5 штук, но менее 20; 3) объем заказа не менее

20 штук.

Независимо от того, в каком объеме продукт был зака-

зан,

мы можем рассматривать этот заказ как осуществле-

ние

одного

только

одного

из

указанных

событий.

Событие,

связанное

с наблюдением x

соответствует

номеру интерва-

ла, в котором оказывается наблюдение.

Любое

возможное

наблюдение должно либо быть равным одной из границ,

либо оказаться

между

двумя

соседними границами, т. е.

имеется только одно k, такое, что Хъ

i < x

^ Хъ.

Поэтому

мы связываем с наблюдением x

событие к. Это оз-

начает, что первая граница событий Х

должна быть мень-

ше,

чем любое наблюдение, которое может иметь место, и

последняя

граница Х

должна быть больше, чем любое воз-

можное наблюдение. Так как нельзя быть абсолютно уве-

ренным,

что наблюдаемые величины

будут

ограничены,

то

возможны две альтернативы конструирования системы. Од-

на

состоит

том,

чтобы

положить Х

= — ооиХ

= + °°.

Другой

путь

— положить Хо столь

малым,

а Х

столь боль-

шим

конечным числом, чтобы можно было ожидать, что ре-

альные наблюдения

будут

находиться в этих пределах. Тог-

да для случая, когда появляется наблюденное значение,

выходящее за установленные пределы,

следует

обеспечить

выработку особого сигнала для вмешательства исследовате-

ля,

который

должен проанализировать

неожиданные

наблю-

дения,

прежде чем обрабатывать их автоматически.

Рассмотрим

простой метод оценки вероятностей Ph (О

наступления различных событий

предложенный Р. Г. Брауном [47]. Так как рассматривает-

ся

полная система п несовместных событий, то степеней сво-

боды

будет

п— 1, ибо сумма вероятностей должна быть

равна

единице, т. е. не все п значений P

независимы.

Анализ прошлых данных или суждение о

будущем

дела-

ет возможным установить границы событий и сделать на-

чальные,

хотя

бы

грубые,

оценки вероятностей различных

событий P

(0), k = 1,2, . . ., п. Пусть наблюдение x

момент t

свидетельствует

о наступлении события k. Пост-

роим

я-мерный вектор-столбец

(*), который имеет п — 1

нулевую

компоненту, а k-я компонента равна единице.

Предыдущие оценки п вероятностей можно рассматривать

как

п-компонентный вектор-столбец P(t~-l). Процесс

пересмотра этих оценок с

учетом

текущей информации яв-

ляется экспоненциальным сглаживанием по правилу

Каждая компонента вектора модифицируется -простым

экспоненциальным

сглаживанием нуля

или

единицы.

На-

пример,

если исследуется система

из 3

событий

наблю-

дение означает наступление второго,

то

Так

как Р (t— 1)

является вектором вероятностей,

то

все его компоненты должны быть неотрицательны

и их

сум-

ма должна быть точно равна

Рассмотренный процесс векторного сглаживания не мо-

жет сделать компоненту

отрицательной,

сумма итоговых

компонент

та

же,

что

сумма

их

прежних значении. Следо-

вательно, если

$ (*

I) является вероятностным вектором,

КотрТсобытие

Если закон распределения наблю-

денных значений

не меняется,

то

ма«шчесш°жда.

ние

значения

i-й

компоненты вектора U Ю,

««*»??

сглаживанию, точно равно действительной вероятности^

наступления события

i и

математическое ожидание оценки

равно действительной вероятности

Вероятность того,

что

придется сглаживать единицу,

равна

Л, а

вероятность того,

что

будем

сглаживать нуль,

равна 1 2- Р,.

Легко подсчитать, что

Ья

компонента векто-

pa U

характеризуется дисперсией

(1 ~-

го-

Выражая дисперсию

результата

экспоненциального

сглаживания через дисперсию на

входе,

получим дисперсию

оценки

вероятности наступления t-ro события:

где

а —

постоянная сглаживания.

nmv

innM

««

Таким

образом, имеются

два

способа «««яЩРомнм

системы, которые наиболее предпочтительны. Границы

со

бытии целесообразно выбирать так, чтобы

Рк

была

°чень

большой (близкой

к 1)

или очень маленькой (почти 0).

это

обеспечит

малую

дисперсию оценок компонент вектора

вероятностей.

/1—1866

Если форма распределения со временем меняется, то

может

быть

использована большая

постоянная

сглаживания,

для того чтобы быстро уменьшить влияние прежних данных.

наоборот, если вероятностное распределение

постоянно

во

времени, то нет

нужды

уменьшать влияние старых данных,

для уменьшения дисперсии оценок можно использовать

меньшую постоянную сглаживания.

Модель предназначается для изучения, например, спро-

са на отдельные виды товаров по возрастным группам, эво-

люции распределения семейных

бюджетов

по статьям рас-

ходов,

распределения

сумм

текущих вкладов и

других

яв-

лений

экономической жизни.

§ 2. СЕЗОННЫЕ МОДЕЛИ

В экономике многие явления характеризуются

периодически повторяющимися сезонными эффектами. Со-

ответственно временные ряды, их отражающие, содержат

периодические сезонные колебания. Эти ряды и их колеба-

ния

можно представить как генерируемые моделями

двух

основных типов: моделями с мультипликативными и с ад-

дитивными коэффициентами сезонности.

Модели первого типа имеют вид:

где динамика величины a

lt t

характеризует тенденцию

раз«

вития процесса;

fu ft-x,

•••>

h-i

i~ коэффициенты сезонности;

/ — количество фаз в полном сезонном цикле (если ряд

представляет месячные наблюдения, то в экономике обычно

/ — 12, при квартальных данных / = 4 и т. п.);

— неавтокоррелированный шум с нулевым математи-

ческим ожиданием.

Модели второго типа записываются как:

где величина

(h,

описывает тенденцию развития процес-

са;

ёи gt -it

•...

gt -

i—аддитивные

коэффициенты

сезон-

ности;

/ — количество фаз в полном сезонном цикле: