Lewis R.I. Turbomachinery Performance Analysis

244

Ducted propellers and fans

Pitch datum line

%

Fig. 8.22 Definition

of blade pitch angle j~p

As we have seen already from Eqn (8.79), the predicted thrust ratio z can be

expressed as a function of CT only irrespective of propeller blade geometry. This

is borne out by Fig. 8.21(a) which compares the predicted "r(CT) characteristic with

experimental results adapted from the experimental data published by Van Manen

(1962) for the additional pitch ratios

P/D

= 0.6 and 1.6. Results for

P/D

= 1.0 have

already been shown in Fig. 8.18 and have been omitted here to emphasise the

negligible influence of the pitch change. Blade geometric pitch P at any radius r is

defined as

P = 2~rr tan

tip

(8.87)

where

tip

is the geometric pitch angle marked out by the pitch datum line, Fig. 8.22,

tangential to the pressure side of the propeller blade. The geometric pitch P is

frequently constant for sections at all radii of a given propeller, but should P actually

vary, the value at 70% of tip radius is adopted as the geometric mean pitch.

The Ka 4-55 propeller considered above is designed for a uniform pitch ratio

P/D

= 1.0.

The results shown in Figs 8.18 and 8.21 correspond to blade setting angles/3p of

10.81 ~ 17.66 ~ and 26.99 ~ respectively and in effect represent the characteristics of

three completely different propellers operating within the same N.S.M.B. 19A duct.

The three related experimental "r(CT) conform closely to the single theoretical

characteristic predicted by Eqn (8.79) and thus demonstrate dramatically the almost

total control over the thrust ratio z imposed by the duct geometry.

On the other hand, qui~e different J(Ca-, z) characteristics are obtained for the three

blade settings, demonstrating, as expected, the close relationship between advance

coefficient J =

Va/nD

and blade geometric pitch ratio

P/D.

Once again the curves

predicted by the simple theory presented above agree with experimental tests

remarkably well, with significant errors to be found only at very low thrust

coefficients. Balabaskaran (1982) undertook extensive aerodynamic investigations of

this particular ducted propeller, confirming both the towing tank experimentation of

Van Manen (1962) and the above fairly modest performance prediction method. He

was able to improve upon this by using cascade theory such as that forthcoming from

the program CASCADE provided with this book, enabling him to remove the

assumption adopted in Section 8.5.2 of constant fluid deflection e.

9

Selected supporting

dynamic analysis

fluid

Introduction

An overview of the overall design and performance analysis for a multi-stage axial

turbine was presented in Chapter 3, Fig. 3.2, which put into context the three

computer programs FIPSI, CASCADE and STACK provided with this book. Table

9.1 summarises the main stages of this overall design sequence.

Table 9.1 Main stages of the overall design sequence for turbomachines

Task Program

(a)

(b)

(c)

II (d)

III (e)

Initial duty specification.

Use of dimensionless parameters (e.g. th, ~ data) for

overall design choices and performance analysis.

Detailed thermodynamic design leading to the definition

of velocity triangles.

Detailed fluid dynamic design to generate blade shapes

which will produce the required velocity triangles. This

involves:

(i) Cascade analysis.

(ii) Meridional analysis.

Mechanical design:

(i) Generation of blade shapes and stacking of profiles

to form a complete blade.

(ii) Stress and vibration analyses.

FIPSI

CASCADE

STACK

The main thrust of this book so far has been to provide an analytical framework

which links items (a), (b) and (c) for axial turbines (Chapter 3), axial compressors

and fans (Chapter 4), mixed-flow and radial turbomachines (Chapter 7), and ducted

propellers and fans (Chapter 8). For example, the computer program FIPSI enables

the reader to complete a full thermodynamic layout for a multi-stage gas turbine with

cross-checks on selection of stage duty coefficients (~b, ~) and related stage efficiency,

hub reaction and Mach number levels. FIPSI delivers a complete specification of

velocity triangles from hub to casing as input to stage (d), aerodynamic design.

The main purpose of the present chapter is to provide the theoretical basis

underlying the program CASCADE, which executes the double task of creating blade

geometry as described in Section 2.4 followed by fluid flow analysis to predict outlet

angle 132 for the given inlet angle /31, and the related blade surface pressure

246

Selected supporting fluid dynamic analysis

Fig. 9.1 (a) Boundary layer and (b)

surface vorticity equivalent for potential flow

modelling; (c)

self-convection of a surface vorticity sheet

distribution. CASCADE thus enables the reader to design blade profiles which will

produce the specified velocity triangles and also to predict off-design performance

of the chosen blading. This will be covered in Sections 9.1 to 9.4. The particular type

of analysis adopted here is the vortex element boundary integral method which is

relatively simple to commit to computer code and economic to run. Although viscous

constraints and aerodynamic loading indices such as diffusion factors have been

discussed in Chapter 2, the present treatment will be limited only to incompressible

inviscid flows. In his research monograph

Vortex Element Methods for Fluid Dynamic

Analysis of Engineering Systems

(Lewis, 1991), the present author has extensively

reviewed and expounded the fundamentals of this powerful and flexible flow analysis

technique with applications to a wide range of turbomachinery configurations

including extensions to vortex cloud simulation of viscous fluid flows. The only

applications additional to cascades to be summarised in this chapter will be the

extension of surface vorticity modelling to axisymmetric flow past bodies of

revolution, ducts and ducted propellers, Section 9.5.

9.1 The physical basis of surface vorticity modelling

In all real fluid flows a boundary shear layer exists adjacent to any solid surface, Fig.

9.1(a), containing sufficient vorticity to reduce the fluid velocity from Vs at the outer

edge a-b of the shear layer to zero on the wall c-d just inside the shear layer. The

vorticity is continuously convected downstream and replenished by convection from

upstream and by the creation of more vorticity in the slip-flow or sub-layer adjacent

to the wall. This new vorticity is then diffused away from the wall by the fluid

9.1 The physical basis of surface vorticity modelling

247

"y(s)ds

vorticity sheet

d e

Vsi

I_ _1

I~ -1

Fig. 9.2 Enlarged view

of surface vorticity element

viscosity, thus maintaining the shear profile of the boundary layer. Motion within

the boundary layer therefore involves a balance between dynamic normal stresses

due to convection and tangential shear stresses due to viscous action. The Reynolds

number Re represents the ratio between these stresses. Let us define Re in terms

of a representative body length l, namely Re =

(vsl)/v.

If Re is increased by

progressively reducing the kinematic viscosity v, the diminishing influence of viscous

diffusion will result in a thinner boundary layer. As Re ~ oo so the boundary layer

transforms into an infinitely thin vorticity sheet as illustrated by Fig. 9.1(b) and this

concept forms the basis of the physical model underlying the surface vorticity method

of potential flow analysis. Thus in inviscid 'potential' flows the bounding surface of

any body may be represented by a surface vorticity sheet of strength 7(s) per unit

length at point s on the surface. Two observations may be made at this point:

(1) The velocity jumps discontinuously from zero below the vorticity sheet at

points actually on the body surface to Vs just outside the vorticity sheet.

(2) The vorticity sheet convects itself along the surface with velocity v~ = lvs,

implying that vorticity must be supplied from upstream, Fig. 9.1(c).

Item (1) suggests a suitable boundary condition to impose at the body surface later

for fluid flow modelling, namely that the velocity Vsi just inside the vorticity sheet

and parallel to the surface is to be zero:

Psi----O (9.1)

Let us now define the contour abcd surrounding a small element ds of the surface

vorticity sheet, Fig. 9.2, where ab and dc are parallel to the streamlines while da

and bc are vanishingly small. The circulation around abcd, defined clockwise positive,

may be equated to the total amount of vorticity enclosed by the contour, that is

(Vso -- l,'si ) (iS "- )t(S) ds

(9.2)

Introducing Eqn (9.1), this reduces to

7(s) = Vso = Vs (9.3)

In other words the local vortex sheet strength

7(s)

is exactly equal to the surface

velocity Vs in potential flow past a body. Equations (9.1) and (9.3) thus provide the

key to surface vorticity modelling of potential flows as originally propounded by E.

248

Selected supporting fluid dynamic analysis

Fig. 9,3 Surface vorticity model to simulate flow of a uniform stream Vs past a plane wall: (a)

infinite

vortex sheet 7(s) between x = __ oo; (b) vortex sheet 7(s) plus uniform stream 7(s)/2

Martensen (1959), often referred to as the

Martensen method.

The procedure may

be summarised as follows:

(1)

(2)

(3)

(4)

The body surface is covered by a surface vorticity sheet of initially unknown

strength 7(s).

A surface boundary condition Vsi = 0 is imposed on the inner surface of the

sheet. This is stated in the form of an integral equation to be derived in the

next section.

The integral equation is solved for a selection of discrete surface vortex

elements at surface locations

Sn

resulting in the required

7(Sn)

values.

The local surface velocity

Vsn

follows directly from Eqn (9.3) since

Vsn---- ]/(Sn).

9.1.1 Surface vorticity simulation of flow past a plane wall

A simple example of surface vorticity modelling which helps to bring out the essential

features is illustrated in Fig. 9.3, namely flow past a plane wall. Let us consider first

the velocity field induced by a vortex sheet of strength 7(s) lying along the x-axis

between +o0, Fig. 9.3(a). The vorticity will induce uniform velocity fields parallel

to the x-axis but in opposite directions above and below the sheet as illustrated,

Vsl = -Vsu. By taking the circulation around the element abcd as before, for this case

we obtain

'y(S) ds = Vsu ds - Vsl as ~- 2Vsu ds

9.1 The physical basis of surface vorticity modelling

249

Surface vorticity

el;snm;dnt n S~m

U=

Voo

Fig. 9.4 Surface vorticity model for flow past a two-dimensional body in a uniform stream IN=

resulting in

Vsu "- -- Vsl-'- 89 (9.4)

If we now superimpose a uniform stream of strength Vsu parallel to the x-axis over

the whole flow field, the outcome will be as illustrated in Fig. 9.3(b). Above the x-axis

the velocity will be that of a uniform stream of strength Vs =

y(s).

Below the x-axis

the velocity will be zero, so that we may replace this by a solid boundary. It follows

also from this argument that the vortex sheet of the real flow convects itself parallel

to the body surface with velocity Vc = Vsu =

7(s)/2.

9.1.2 Martensen's boundary integral equation

We consider next the flow past a two-dimensional body immersed in a uniform

stream Wo~ inclined to the x-axis at an angle aoo, Fig. 9.4. Applying the principles

just outlined, the flow may be modelled by clothing the body surface with a vorticity

sheet of appropriate strength

7(s)

where s is measured clockwise around the body

perimeter from some zero datum O such as the leading edge in the case of an

aerofoil. Now the velocity

dqm n

at

some surface location

Sm

induced by the vortex

element

7(Sn)dSn

at location

Sn

will be normal to the radial vector

rm,

and will be

of magnitude

T(sn)dsn

dqm n

-- (9.5)

2 7rr mn

250

Selected supporting fluid dynamic analysis

In order to state the surface boundary condition, Eqn (9.1),

dqm n

needs to be resolved

parallel to the body surface at

Sm,

namely

dvsm n= dqm ncO,s tim +'~- t~mn =

COS

~m d- -~ -- (~mn

)t(Sn)dSn

27rtmn

(9.6)

where

tim

is the body profile slope at

s m.

For computational purposes it proves more

convenient to first express the components of

dqm n

parallel to the x- and y-axes in

terms of the

(x,y)

coordinates of points

Sm

and

Sn.

Thus

dUmn=]t(sn)dsn

(Ym-Yn)

27rrmn

sin ~bmn =

27rr2mn

")t(Sn)dSn

dVmn =~t(Sn)dSn ( Xm-Xn )

- 27rrmn

cost~mn=-

2,trr2mn )t(sn)dsn

(9.7)

Resolving

d Umn

and

d Vmn

parallel to the surface at

s m

and adding them we obtain

dvcm n -- dUmn

cos

tim -F dVmn

sin

tim

1 {(Ym--yn)COSflm--(Xm--Xn)Sinflm)

-

2zr

(Xm -- Xn) 2 + (Ym -- Yn) 2 ')t(Sn) dSn

(9.8)

The self-convection velocity

Vcm

parallel to

s m

due to the entire sheet can now be

obtained by integration of Eqn (9.8) to yield

Vcm=~dvcmn=~k(sm, Sn)]t(sn)dsn

(9.9)

where the coupling coefficient

k(Sm,Sn)

linking points

s m

and

s n

is given by

1 { (Ym-

k(sm, Sn) = "~

Yn)

COS

~m -- (Xm -- Xn)

sin

tim

(X m -- Xn) 2 -b (Ym -- Yn) 2

(9.10)

Now the contour integral in Eqn (9.9) actually runs through the centre of the sheet

and gives us the convection velocity equivalent to Vc. Fig. 9.3. As indicated in the

previous section we must therefore subtract

y(Sn)/2

to obtain the velocity just inside

the sheet, namely

Vsmi = _ 1 ~(Sm) + ~ k(sm, S n) ")t(Sn) dsn

(9.11)

In addition to this we must account for the component of the uniform stream resolved

parallel to the surface at

Sm,

namely

Wsm = Uoo

cos ~m + Voo

sin

~m

= Woo(cos otoo cos ~m +

sin aoo sin

~m)

(9.12)

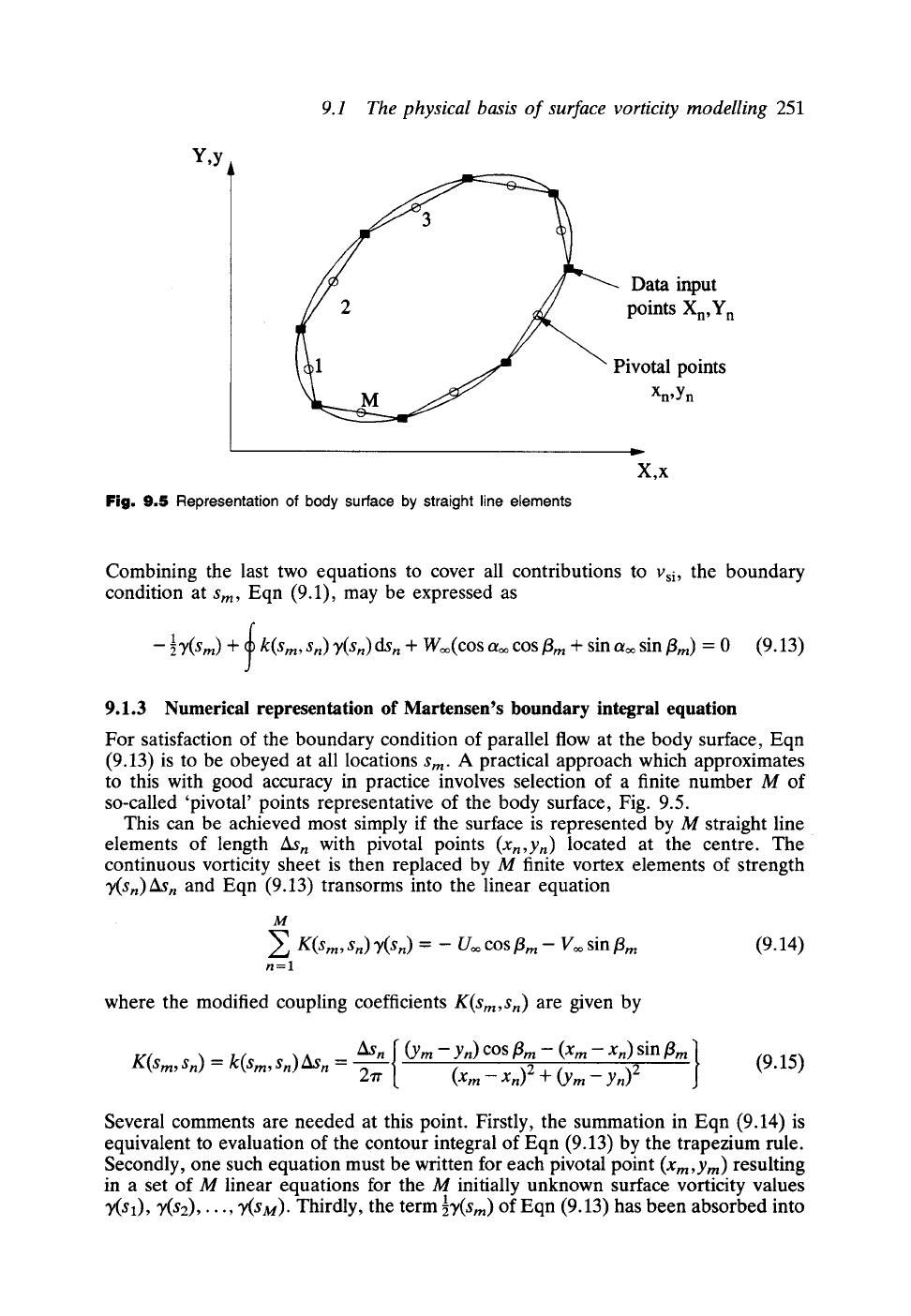
Y,y

9.1

The physical basis of surface vorticity modelling

251

Data input

points

Xn,

Yn

M

Pivotal points

Xn,Yn

Fig.

9.5 Representation of body surface by straight line elements

...._

v

X,x

Combining the last two equations to cover all contributions to Vsi , the boundary

condition at

Sm,

Eqn (9.1), may be expressed as

-- ~]/(Sm) + k(s m, Sn) )t(Sn) dsn

+ Woo(COS O~oo COS ~m +

sin a~ sin

~m) = 0

(9.13)

9.1.3 Numerical representation of Martensen's boundary integral equation

For satisfaction of the boundary condition of parallel flow at the body surface, Eqn

(9.13) is to be obeyed at all locations

Sm.

A practical approach which approximates

to this with good accuracy in practice involves selection of a finite number M of

so-called 'pivotal' points representative of the body surface, Fig. 9.5.

This can be achieved most simply if the surface is represented by M straight line

elements of length

/~kS n

with pivotal points

(Xn,Yn)

located at the centre. The

continuous vorticity sheet is then replaced by M finite vortex elements of strength

7(s~)ASn

and Eqn (9.13) transorms into the linear equation

M

g(sm, Sn) )t(Sn) = - U~

cos

tim - Voo

sin

tim (9.14)

n=l

where the modified coupling coefficients

K(sm,Sn) are

given by

aSn{

K(S m, Sn) = k(sm, Sn) ~ks n =

(Ym -- Yn)

COS

~m -- (Xm -- Xn)

sin

tim ]

(Xm -- Xn) 2 + (Ym -- Yn) 2

(9.15)

Several comments are needed at this point. Firstly, the summation in Eqn (9.14) is

equivalent to evaluation of the contour integral of Eqn (9.13) by the trapezium rule.

Secondly, one such equation must be written for each pivotal point

(Xm,Ym)

resulting

in a set of M linear equations for the M initially unknown surface vorticity values

3'(Sl), 7(s2),...,

7(SM).

Thirdly, the term

89

of Eqn (9.13) has been absorbed into

252

Selected supporting fluid dynamic analysis

m

rm

Fig. 9.6 Curvature of element m

the coupling coefficient g(sm,Sm) which is also indeterminate, a problem to be de~ilt

with in the next section.

9.1.4 The self-inducing coupling coefficient

K(sm, Sm)

Following up this last point, the coupling coefficient K(sm,Sm) may be expressed as

g(Sm, Sm) = _ 1 + g~nm

(9.16)

where, from Eqn (9.15), gmm is given by

Asm lim

[ (ym - yn) cOS flm - (xm - xn) sin flm }

(917)

Kmm -

2.a"

Sm--,Sn (Xm -- Xn) 2 + (Ym -- Yn) 2

Since both numerator and denominator approach zero as

s m

--->

S n

this expression is

finite but indeterminate. As shown in full by Lewis (1991, page 23), application of

L'Hospital's rule twice over results in

I(mm

ASm{ -d2ym [dX2 }

2"rt" [l + (dym/dxm)2] 3/2

_ l~Sm ~ A[~m

47rrm 4zr

(9.18)

where

rm

is the internal radius of curvature of element m and Aflm is the change

in profile slope from one end of the element to the other, Fig. 9.6.

Thus the so-called 'self-inducing' coupling coefficient K(sm,Sm) , which represents

the velocity induced parallel to the surface at

Sm

by element

~kS m

itself, may be

expressed with good approximation by

K(sm, Sm) =

1

A[~ m

2 4zr

1

2

~m+l -- tim-1

87r

(9.19)

9.2 Computational scheme for flow past a body in a uniform stream

253

where

Aflm

is evaluated as half the change in slope of the neighbouring elements

Sm--

1

and

Sin+

1,

namely

l(flm+ 1

--

tim-- 1)-

9.2

Computational scheme for flow past a body in a

uniform stream

The linear equations (9.14) have the matrix form

Kll K12 K13 9

K21 K22 K23 ...

K31 K32 K33 ...

9 9 9

KM1 KM2 KM3

KIM I

T(S1) ' rhSl

K2M I

Y(S2) rhs2

K3M. I

')t(S3)"

= rhs3.

KMM /

"}/(S M)

rhSM

(9.20)

(Coupling coefficient matrix)

Vorticity rhs

vector vector

with the simplified coupling coefficient notation

Kmn

sides

=-- g(sm,Sn)

and the right-hand

rhsm = -Uoo

cos tim -

Voo sin

~m

(9.21)

Generally speaking the dominant coefficients of the coupling coefficient matrix will

be those lying on the leading diagonal

K11 , K22 , etc.,

and solution of the equations

by matrix inversion is appropriate. A suitable numerical sequence is then as

follows"

(1) Input M + 1 sets of raw body profile data coordinates (An, Yn) as illustrated

in Fig. 9.5. Note that for profile closure

XM+I

= X1 and

u = Y1.

(2) Define the pivotal points

(Xn,Yn)

and element slopes/3n, namely

Xn -- 89 Jr"

gn+l),

Yn -" 89 -1- Yn+

1) (9.22)

~n'-arctan(

yn+l-yn )Xn+l

_ Xn

(9.23)

(3) Set up the coupling coefficient matrix using Eqns (9.15) and (9.19).

(4) Evaluate the rhs vector using Eqn (9.21).

(5) Invert the coupling coefficient matrix.

(6) Multiply the rhs vector by the inverted matrix to obtain the solution

=

Example 9.1 Flow past a circular cylinder

The exact solution for the flow of a uniform stream Uoo past a circular cylinder is

well known (Batchelor, 1970), the surface velocity being given by

Vs = 2Uoo cos th (9.24)

Lewis R.I. Turbomachinery Performance Analysis

Подождите немного. Документ загружается.