Lewis R.I. Turbomachinery Performance Analysis

224

Ducted propellers and fans

1.8-

Vp

7.=

VP~ -~~.._ Kort Nozzles

1.,

1.0

0.8

0.9

1.0 Open ~Irooellers

1.1

_._. 1.2------

~~ 1.3-

~---

1.4~"

'I

Pump Jets

0.6-

0.5 1.0 1.5 V~.,,'/r'

T

2.0 2.5

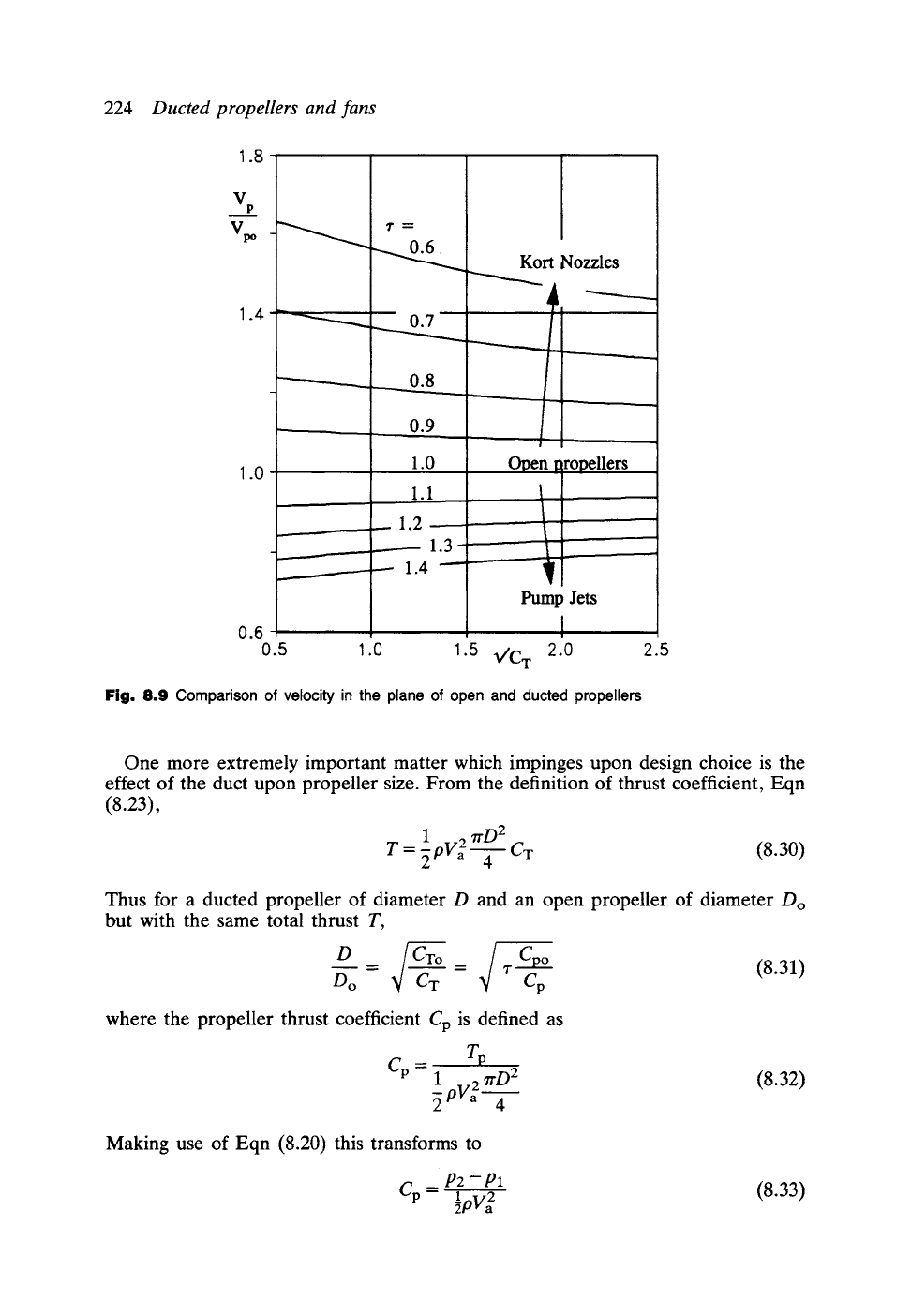
Fig. 8.9 Comparison of velocity in the plane of open and ducted propellers

One more extremely important matter which impinges upon design choice is the

effect of the duct upon propeller size. From the definition of thrust coefficient, Eqn

(8.23),

1 7rD 2

T = -~ pV 2 --~ CT

(8.30)

Thus for a ducted propeller of diameter D and an open propeller of diameter Do

but with the same total thrust T,

D ;.CT~ / Cp~

(8.31)

Do = ~TT

= T Cp

where the propeller thrust coefficient Cp is defined as

Tp

Cp =

1

"r/'O 2

(8.32)

"2 pv2 4

Making use of Eqn (8.20) this transforms to

Cp = P2 -Pl

1 2

(8.33)

~pv~

8.4 More detailed performance analysis for ducted propellers

225

1.6

Cp 1.4 ~~k~~~

Cpo k~ x Pump Jets

1.2 '! ~ d

0.8 Kort ~ \

,,,ozz, s

r = 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3

0.6

" "~

........

0.50 0.75 1.00 1.25 1.50

D/D o

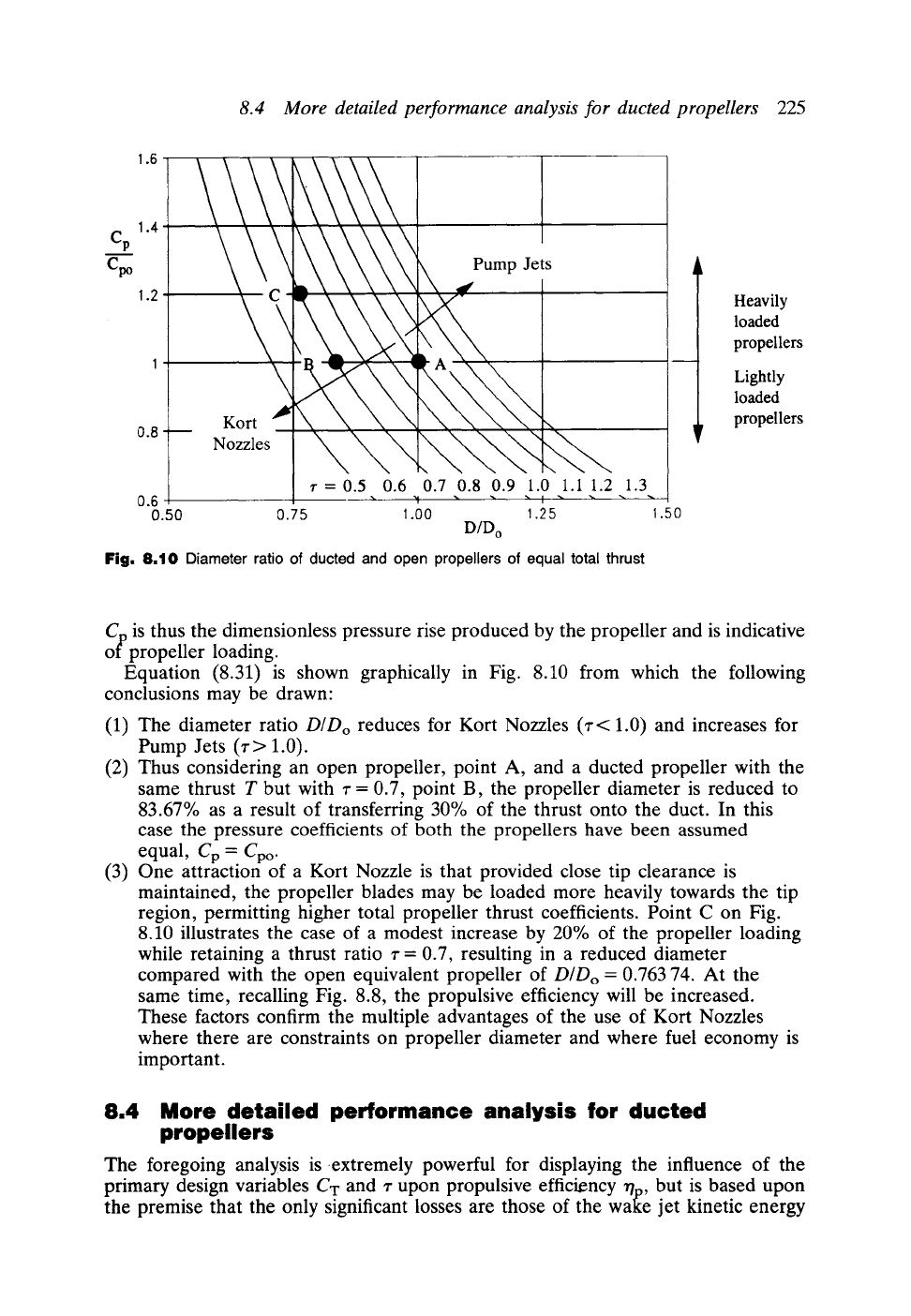
Fig.

8.10 Diameter ratio of ducted and open propellers of equal total thrust

Heavily

loaded

propellers

Lightly

loaded

propellers

C.. is thus the dimensionless pressure rise produced by the propeller and is indicative

ot vpropeller loading.

Equation (8.31) is shown graphically in Fig. 8.10 from which the following

conclusions may be drawn:

(1)

(2)

(3)

The diameter ratio

D/Do

reduces for Kort Nozzles (z< 1.0) and increases for

Pump Jets (r> 1.0).

Thus considering an open propeller, point A, and a ducted propeller with the

same thrust T but with r = 0.7, point B, the propeller diameter is reduced to

83.67% as a result of transferring 30% of the thrust onto the duct. In this

case the pressure coefficients of both the propellers have been assumed

equal, Cp = Cpo.

One attraction of a Kort Nozzle is that provided close tip clearance is

maintained, the propeller blades may be loaded more heavily towards the tip

region, permitting higher total propeller thrust coefficients. Point C on Fig.

8.10 illustrates the case of a modest increase by 20% of the propeller loading

while retaining a thrust ratio r = 0.7, resulting in a reduced diameter

compared with the open equivalent propeller of

D/Do

= 0.763 74. At the

same time, recalling Fig. 8.8, the propulsive efficiency will be increased.

These factors confirm the multiple advantages of the use of Kort Nozzles

where there are constraints on propeller diameter and where fuel economy is

important.

8.4

More detailed performance analysis for ducted

propellers

The foregoing analysis is extremely powerful for displaying the influence of the

primary design variables CT and z upon propulsive efficiency rl , but is based upon

the premise that the only significant losses are those of the wa~e jet kinetic energy

226

Ducted propellers and fans

dissipation Ew. Replacing the shaft input power by P =

TVa,

Eqn (8.12), the

propulsive efficiency, Eqn (8.11), may then be written in the approximate form

1 1

jet KE losses Ew (8.34)

1+ 1+

shaft power

TV a

As shown by Lewis (1972) in a comprehensive paper on ducted propeller performance

analysis as seen from a turbomachine viewpoint, the last equation should be expanded

to include losses from four other sources"

r/p =

ew Sw Fp Fa TL (8.35)

1+ TVa +

rVa ~- rVa q- rVa -I-~rVa

Ew and Sw now cover kinetic energy losses due to both axial and swirl velocities in

the downstream jet, Fp and Fd account for propeller and duct frictional losses, and

TL accounts for the tip leakage losses at the propeller blade tips. Each loss is

normalised here by the thrust power TVa. In order to derive expressions for these

in terms of design variables, some considerations of dimensional analysis are

necessary at this point.

8.4.1 Detailed dimensional analysis for ducted propellers

The losses and hence the propulsive efficiency depend upon a large number of

operational and geometric variables, most of which are at the outset independent

design variables, r/p may thus be expressed as a function of these variables grouped

as follows:

r/p = f(T, Va,

n, r, D, rh, ld, lp, Z, 6, CDd, CDp) (8.36)

System Machine Frictional

variables design coefficients

variables

(rev s- ), rh is hub radius, ld is duct length, lp is propeller

where n is rotational speed 1

chord, Z is the number of blades and 8 is the tip clearance.

System variables

would

normally be prescribed for the designer in the initial specification.

Frictional

coefficients

CDd for the duct and CDp for the propeller will depend upon both the

machine shape and the operating conditions and thus, like r/p, are dependent

variables.

By formation of conventionally accepted dimensionless groupings, the number of

variables may be reduced spontaneously from 12 to nine, resulting in

rip = f(~f , ~,r' h , ld/D,v t/lp, 8/D,~

,~CDd'yCDp) (8.37)

System Machine Frictional

variables design coefficients

variables

8.4 More detailed performance analysis for ducted propellers

227

where in addition to previous definitions of CT and z,

V

a

(advance coefficient) (8.38)

J= nD

h = rh

D/2

(hub/tip ratio) (8.39)

t

lp

zrD

= (propeller tip pitch/chord ratio) (8.40)

Zlp

A number of alternative system parameters are frequently used in the propeller

literature. Although not strictly pertinent to the present analysis they will be listed

here for completeness, namely,

T ,/r

Kr = p~-n2

r,~4 = -~

CT J2

(thrust coefficient) (8.41)

O

KQ = pn2D 5

(torque coefficient) (8.42)

NP 1/2

(KQ) 1/2

Bp = Va5/2 = 33.08 -~ (loading coefficient) (8.43)

ND

101.27

6v = = (velocity coefficient) (8.44)

Va J

In the last two items the speed of rotation N is expressed in rev min -1, D in feet,

Va in knots and P in horse power.

All the appropriate dimensionless groups involving independent variables have now

been defined and we may proceed to express the various losses in Section 8.4 in terms

of these.

8.4.2 Axial and swirl jet kinetic energy losses

The dimensionless jet axial kinetic energy loss follows from Eqns (8.24) to (8.26),

namely

Ew = 1 (V'I + "rCT-- 1) (8.45)

TV a

2

where the assumption is retained that Vp and V i are constant at all radii. This would

indeed be the case for a free-vortex propeller, which combines uniform loading

Apo = Po2-Pol with a free-vortex swirl

co2r

= constant, Section 5.1. These are also

related through the Euler pump equation

~Po

= co2rf~

p (8.46)

= constant for free-vortex swirl

228 Ducted propellers and fans

Now the swirl kinetic energy created at the propeller plane may be expressed as

I I rt

rt C202 P Vp

2"rrr dr c2o2 r dr

Sw= -T

h 9 h

Substituting for Vp from Eqn (8.28), this becomes

S w -- p'rrVa

- 2----~ (1 + V'I + -rCT)I (8.47)

Making use of the Euler pump equation (8.46), the integral I may be evaluated for

flee-vortex propellers as follows:

I = c2rdr = ( Ap~ 2_1 dr

h h \pfl r

Ap2o Cfiot V2a

= 4p 2 ,tr2 n2 In (l/h) = 16,tr2n2 In (l/h)

(8.48)

where the propeller tip loading coefficient

Go t

is defined as

~Pot

Got--

1 2

(8.49)

~pVa

Now from the definition of thrust coefficient CT, Eqn (8.23),

1 2 "n'D2

TVa=

CT~pVa'- ~ Va

Thus finally, the dimensionless swirl loss of a flee-vortex ducted propeller be-

comes

Sw

TVa

C~ot V2

= 47r 2 rCT n 2 D 2

(1

+ ~/1 + rCT) In (l/h)

_

Cfiot j2

(1 + V' 1 + TCT) In (l/h)

- 4,rr2 rCT

(8.50)

Lewis (1972, Appendix II) has shown that the tip loading coefficient

Go t

may be

expressed for free-vortex ducted propellers through

Cpo t

"rr2(1-h2){ ~/ 2rCTJ21n(1/h)}

= j2

In(l/h) 1 - 1 - ~-0- h-~ (8.51)

so that the swirl loss

SwlTV a

is known explicitly as a function of all the independent

design variables r, Ca-, J and h.

8.4 More detailed performance analysis for ducted propellers 229

1.00

r

r,

0.75

0.50

0.25

0.00 1.25

I

Power law

0.25 0.50 0.75 1.00

Apo/APot

1.00

r

r t

0.75

0.50

0.25

0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5

Co/Cot

(a) (b)

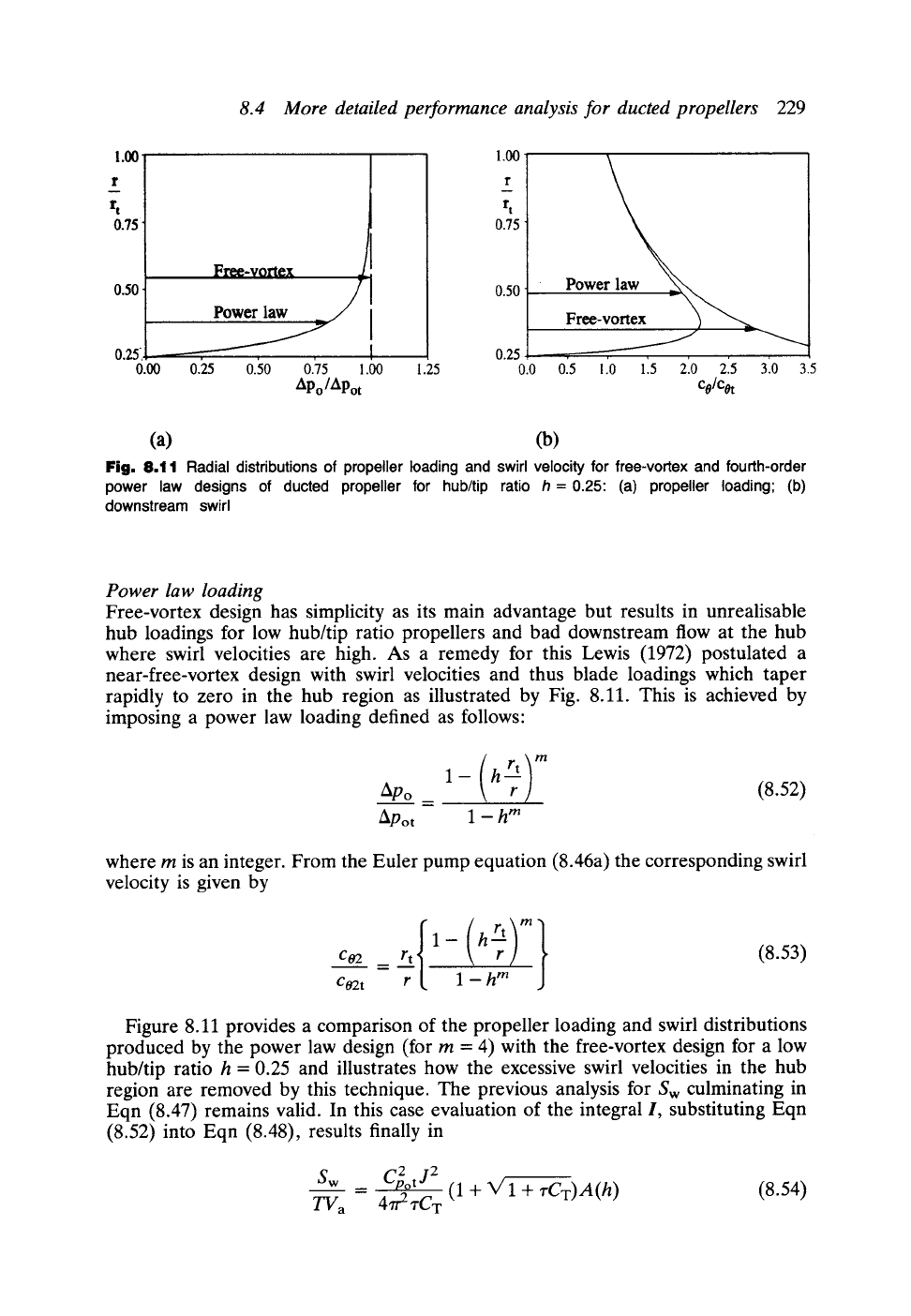
Fig.

8.11 Radial distributions of propeller loading and swirl velocity for free-vortex and fourth-order

power law designs of ducted propeller for hub/tip ratio h = 0.25: (a) propeller loading; (b)

downstream swirl

Power law loading

Free-vortex design has simplicity as its main advantage but results in unrealisable

hub loadings for low hub/tip ratio propellers and bad downstream flow at the hub

where swirl velocities are high. As a remedy for this Lewis (1972) postulated a

near-free-vortex design with swirl velocities and thus blade loadings which taper

rapidly to zero in the hub region as illustrated by Fig. 8.11. This is achieved by

imposing a power law loading defined as follows:

a thrt)m

r (8.52)

Apo t 1 -

h m

where m is an integer. From the Euler pump equation (8.46a) the corresponding swirl

velocity is given by

{l hrt)m}

c02 = r_At r (8.53)

Co2t r 1

-- h m

Figure 8.11 provides a comparison of the propeller loading and swirl distributions

produced by the power law design (for m =4) with the free-vortex design for a low

hub/tip ratio h = 0.25 and illustrates how the excessive swirl velocities in the hub

region are removed by this technique. The previous analysis for Sw culminating in

Eqn (8.47) remains valid. In this case evaluation of the integral I, substituting Eqn

(8.52) into Eqn (8.48), results finally in

Sw _ C:ot J2

TE a

--

4,n.2,rC T (1 + V' 1 + TCT)A(h) (8.54)

230

Ducted propellers and fans

0.3

J-07

_o., o6

._ 0.5 ~,,, ~,._

e~

0.4 ~

~ .

._,~

~: 0.3 ~ .....__...__._,

0.0 0.2 "-'------- -

0.0 0.1 0.2 0.3 0.4 0.5

Hub/tip ratio h

0.3

_c 0.2

0.1

0.0

(a) (b)

J=0.7

o.6,,,

0.5 ~ ~

0.4 ~ ~~~__ ,

~ ~ __.._._____

0.3 ~~._________

0.2

0.1 0.2 0.3 0.4 0.5

Hub/tip ratio h

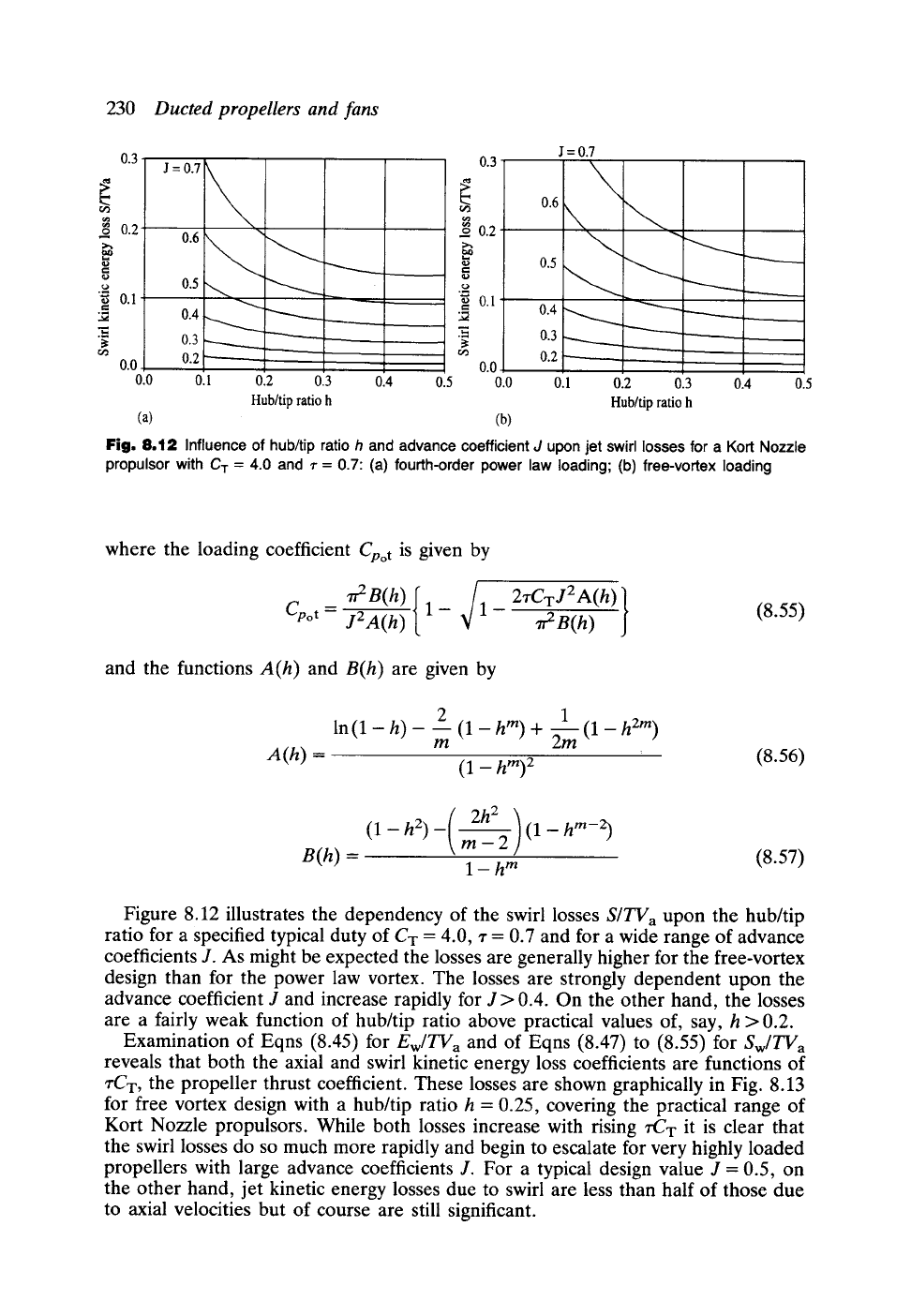
Fig. 8.12 Influence of hub/tip ratio h and advance coefficient d upon jet swirl losses for a Kort Nozzle

propulsor with CT = 4.0 and z = 0.7: (a) fourth-order power law loading; (b) free-vortex loading

where the loading coefficient

Cpo t

is given by

"rr2B(h) [ ~/

2ZCTJ2A(h)}

Cpo t = j2A(h) 1- 1- zr2B(h )

(8.55)

and the functions

A(h)

and

B(h)

are given by

1 h2m)

ln(a

- h) - 2 (1 -

h m) +

(1 -

m

A(h)

= (1 -

hm) 2

(8.56)

(1-h2)-(m-22h2)(1-h

m-z)

B(h) = 1- h m

(8.57)

Figure 8.12 illustrates the dependency of the swirl losses

S[TV a

upon the hub/tip

ratio for a specified typical duty of CT = 4.0, z = 0.7 and for a wide range of advance

coefficients J. As might be expected the losses are generally higher for the free-vortex

design than for the power law vortex. The losses are strongly dependent upon the

advance coefficient J and increase rapidly for J > 0.4. On the other hand, the losses

are a fairly weak function of hub/tip ratio above practical values of, say, h >0.2.

Examination of Eqns (8.45) for

Ew/TV a

and of Eqns (8.47) to (8.55) for

Sw/TVa

reveals that both the axial and swirl kinetic energy loss coefficients are functions of

zCT,

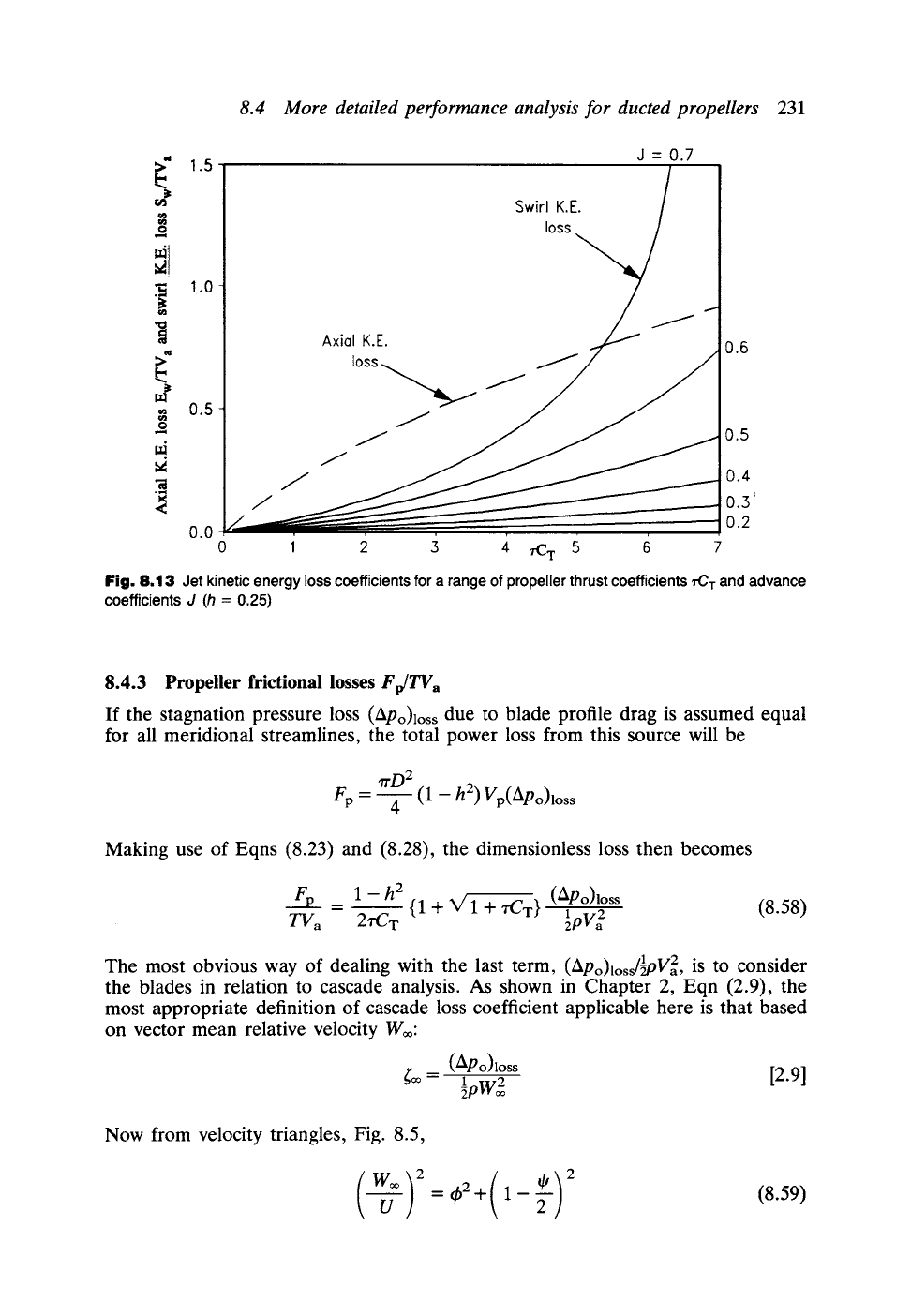
the propeller thrust coefficient. These losses are shown graphically in Fig. 8.13

for free vortex design with a hub/tip ratio h = 0.25, covering the practical range of

Kort Nozzle propulsors. While both losses increase with rising "rCT it is clear that

the swirl losses do so much more rapidly and begin to escalate for very highly loaded

propellers with large advance coefficients J. For a typical design value J = 0.5, on

the other hand, jet kinetic energy losses due to swirl are less than half of those due

to axial velocities but of course are still significant.

8.4 More detailed performance analysis for ducted propellers

231

1.5

~.o

[-,

,~ 0.5

o

ai

N

9 l,,,q

0.0

J-0.7

J

/

Axial K.E.

Ioss~

J

jl

Swirl K.E.

loss

0 1 2 3 4

.rCT

5 6 7

0.6

0.5

0.4

0.3'

0.2

Fig. 8.13 Jet kinetic energy loss coefficients for a range of propeller thrust coefficients

I"C T

and advance

coefficients J (h =

0.25)

8.4.3 Propeller frictional

losses

Fp/TV a

If the stagnation pressure loss (Apo)los s due to blade profile drag is assumed equal

for all meridional streamlines, the total power loss from this source will be

rrD 2

Fp = 4 (1 - h 2) Vp(Apo)los s

Making use of Eqns (8.23) and (8.28), the dimensionless loss then becomes

Fp 1

-- h 2 (Apo)los s (8.58)

TV a =

27"C

T {

1 + V' 1 +

TC T} 1 2

~OVa

1 2

The most obvious way of dealing with the last term,

(Apo)loss/~PVa,

is to consider

the blades in relation to cascade analysis. As shown in Chapter 2, Eqn (2.9), the

most appropriate definition of cascade loss coefficient applicable here is that based

on vector mean relative velocity Woo:

(APo)loss

~'~176 1 2

[2.91

~pW~

Now from velocity triangles, Fig. 8.5,

0 +(1

(8.59)

232 Ducted propellers and fans

Combining these results,

(apohoss

1 2

~pV/,

2 r

If this is now applied to the propeller tip radius D/2, making use of the definition

of advance coefficient J and introducing the rotational speed II = 2~n,

j=Va~rVa (Va) (8.60)

nD = lID~2 = ~r --~

The previous equation then becomes

Substitution of this result into Eqn (8.58) yields finally

1h2 ( t)2}

TVa =

2---~T {I+V'I+'rCT} 7 4~2+ 1----~- sroo (8.61)

= f('r, CT, J, h,

t~t , ~t,

~oo)

The propeller profile losses have thus been expressed as an explicit function of

six independent design variables plus the loss coefficient ~'oo. Losses will thus depend

upon two main groups of design variables:

(1) The overall propulsor duty specification CT, r and J.

(2) The blade row duty (~bt, q't) which has been stated here for the tip section.

As shown in Chapter 2, Eqn (2.8), the cascade loss coefficient ~oo can be expressed

in terms of the profile drag coefficient CDp through

l

~'oo = 7

CDp sec/3oo

l 1]

= 7 CDp--~-t 4, 2

=

f(t/l,

CDp , t~t , ~t)

q't

( 1

(8.62)

Introducing this into Eqn (8.61) we have finally the more useful form

1i ( /

TV a =

2ge

T

{ 1 + V' 1 +

"rC T} ~t t~t2 4-

1 - -~

CDp

(8.63)

= f(T, CT, J,

Ct, Ot,

h, t/l,

CDo)

Propulsor Propeller Machine Cascade

duty duty geometry drag coefficient

8.4 More detailed performance analysis for ducted propellers

233

Although it is helpful to bring out the dependency upon propeller tip duty

(t~t , ~t)

in these expressions, these coefficients themselves may also be expressed in terms

of the propulsor duty (~',

CT, J)

as follows"

and

~t

~t "-

gp _- J Vp = ~J {1 + W'l + zCT} (8.64)

7rnD

1r V a

27rz

~Pot

p(qrnD) 2

-" 1 2 ~ --"

~pVa r

l-h2 {

2 In (l/h)

2,rC T j2

In (l/h)

}

1 - 1 - ,rr2(1 _

h2)2

for flee-vortex loading

B(h) ~/1

= 2~) { 1- -

2"rCTJ2A(h) }

,n.2 B(h) 2

for power-law loading

(8.65)

where

A(h)

and

B(h)

have already been given as Eqns (8.56) and (8.57) respec-

tively.

8.4.4 Duct frictional losses

Fd/TV a

The usual method for defining a suitable drag coefficient is to regard the duct as an

annular aerofoil located in open water of velocity Va. Adopting the conventional

definition of Cd for aerofoils, CDd is then defined as

Drag in open water

CDd = 1 2

(8.66)

~pVa 7rDld

When combined with a propeller, on the other hand, the high velocity on the inner

surface will tend to generate dominating losses and it would seem reasonable to

assume that the duct drag Dd is that corresponding to a uniform stream Vp,

namely

1 2

D d = CDd~pVp 7rDld

The power losses due to duct drag are then

Fd Dd Va

TVa TVa

( )2

4 ld V___IZ CDd

CTDVa

1

(1+

W'l+ "rCT)2(--~)CDd

(8.67)

which may be expressed in the general form

TVa

(8.68)

Lewis R.I. Turbomachinery Performance Analysis

Подождите немного. Документ загружается.