Lewis R.I. Turbomachinery Performance Analysis

194

Mixed-flow and radial turbomachines

7.4

Geometrical techniques for dealing with design and

analysis of mixed-flow cascades

As already discussed in the introduction to Chapter 2, the fully three-dimensional

flow through axial turbomachines can be modelled with sufficient accuracy in most

cases by a series of two-dimensional

blade-to-blade

or

cascade

flows superimposed

upon a circumferentially averaged axisymmetric meridional flow. This strategy was

illustrated in Fig. 2.1 for an axial fan located within a cylindrical annulus. The

intersection of a cylindrical meridional stream surface with the blades then generates

a cylindrical cascade which can be developed into an infinite rectilinear or

straight

cascade in the flat (x,y) plane, Fig. 2.2, by simply unwrapping the cylinder and laying

it flat on the

(x,y)

plane.

Figure 7.11 illustrates the equivalent quasi-two-dimensional modelling of the much

more complex three-dimensional flow through a mixed-flow turbomachine, in this

case the Francis turbine previously considered in Section 7.2, Fig. 7.6(b). The

circumferentially averaged meridional flow for this machine forms a series of coaxial

stream surfaces of revolution between hub and shroud (casing), Fig. 7.11(a), which

enter the inlet guide vanes radially and leave downstream of the runner axially. The

annulus is designed to turn the flow from radial to axial in the zone occupied by the

turbine runner, resulting in a wide range of geometries of the so-called elementary

turbines located on each surface of revolution. Thus along the shroud meridional

surface a-a the flow is predominantly that of an axial turbine. Along the hub stream

surface b-b, on the other hand, the elementary turbine b--b is subject to a very large

radial shift from rl to r2 resulting in large loading contributions due to Coriolis

forces.

A typical stream surface ~o somewhere in between the hub and shroud will intersect

the guide-vanes and runner blades as illustrated in Fig. 7.11(b). The guide-vane blade

profiles then form on this axisymmetric surface what is usually referred to as a radial

(or circular) cascade, stationary in space. The runner blades, on the other hand, form

a mixed-flow (sometimes called radial-axial) cascade rotating on the surface of

revolution.

The geometrical complexity at first sight seems gross by comparison with the axial

machine for which the equivalent two-dimensional cascade model in the (x,y) plane

was so easily obtained, Fig. 2.2. In fact relatively simple geometrical transformations

can be found to convert the radial or mixed-flow blade-to-blade geometry into

equivalent straight cascades and the related procedures required to achieve this will

r 1

] Radial

guide vanes

~- r2

b

i ~ I ~i\

"Runner

blades

j ,

(a) (b)

Fig. 7.11 Intersection of a meridional surface of revolution with the blade rows of a Francis turbine:

(a) meridional streamlines; (b) surface of revolution for meridional streamline ~o

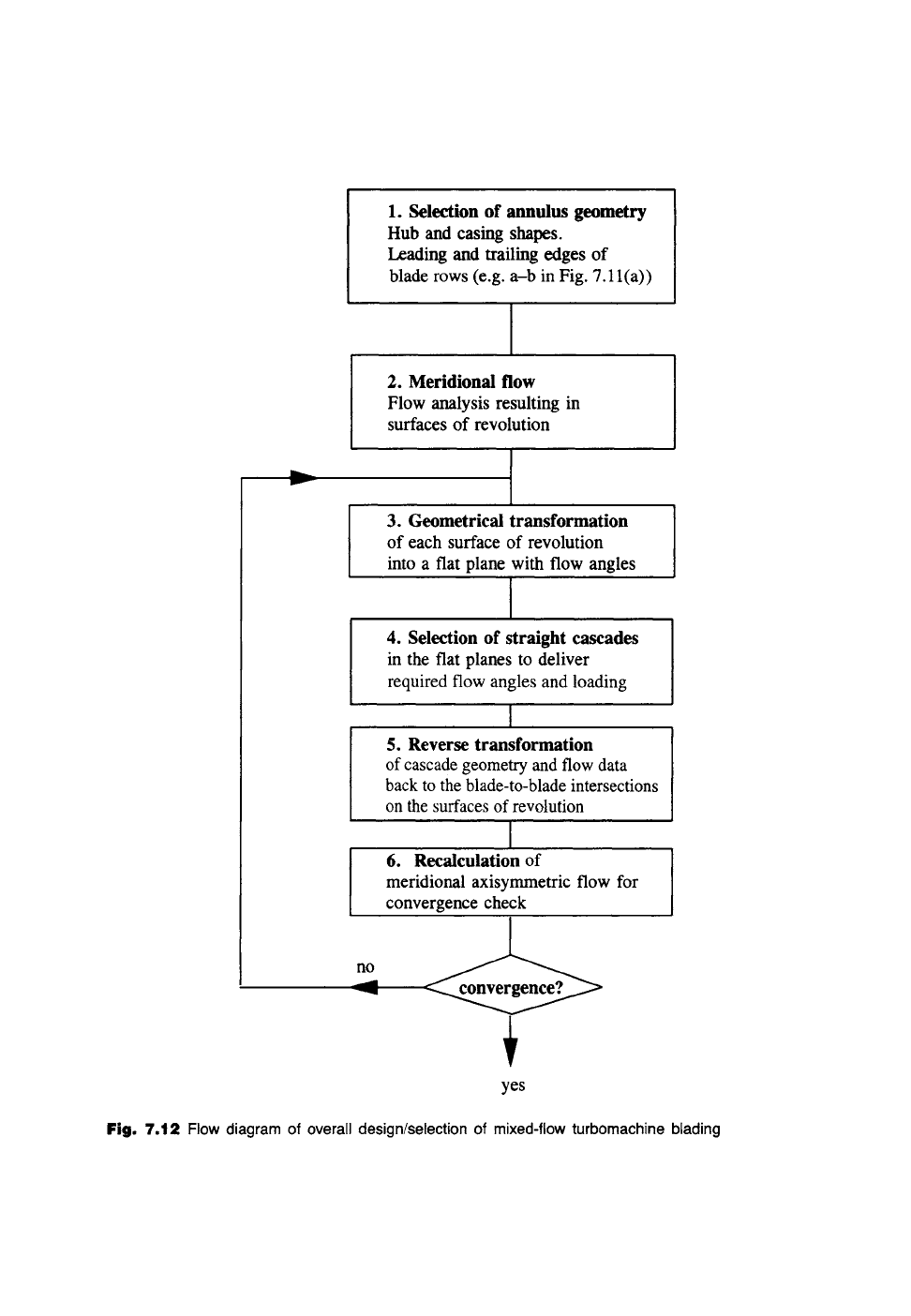
1. Selection of annulus geometry

Hub and casing shapes.

Leading and trailing edges of

blade rows (e.g. a-b in Fig. 7.11 (a))

2. Meridional flow

Flow analysis resulting in

surfaces of revolution

y

3. Geometrical transformation

of each surface of revolution

into a flat plane with flow angles

4. Selection of straight cascades

in the flat planes to deliver

required flow angles and loading

I

5. Reverse transformation

of cascade geometry and flow data

back to the blade-to-blade intersections

on the surfaces of revolution

I

6. Recalculation

of

meridional axisymmetric flow for

convergence check

no

yes

Fig.

7.12 Flow diagram of overall design/selection of mixed-flow turbomachine blading

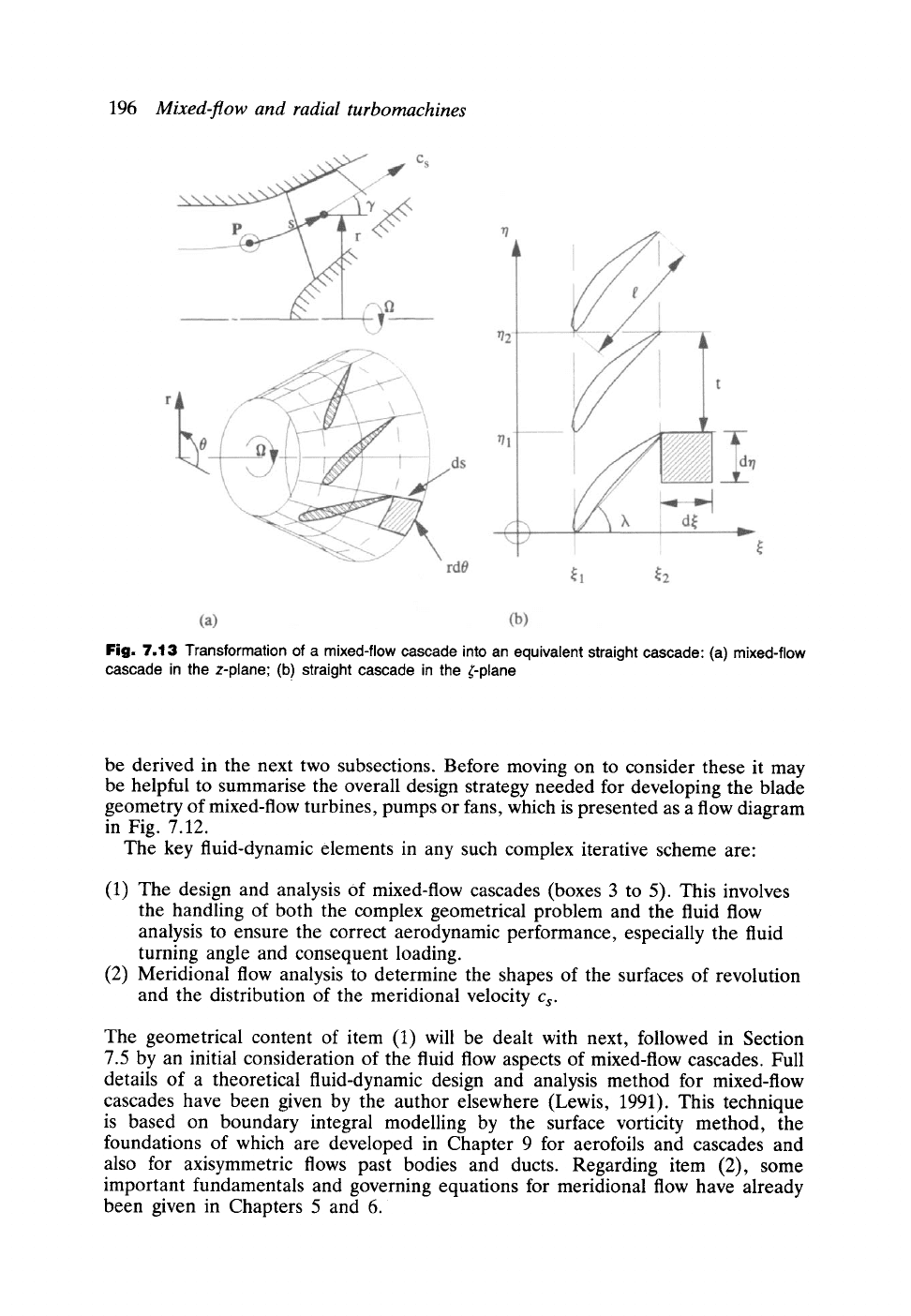
196

Mixed-flow and radial turbomachines

Fig. 7.13 Transformation of a mixed-flow cascade into an equivalent straight cascade" (a) mixed-flow

cascade in the z-plane; (b) straight cascade in the ~'-plane

be derived in the next two subsections. Before moving on to consider these it may

be helpful to summarise the overall design strategy needed for developing the blade

geometry of mixed-flow turbines, pumps or fans, which is presented as a flow diagram

in Fig. 7.12.

The key fluid-dynamic elements in any such complex iterative scheme are:

(1) The design and analysis of mixed-flow cascades (boxes 3 to 5). This involves

the handling of both the complex geometrical problem and the fluid flow

analysis to ensure the correct aerodynamic performance, especially the fluid

turning angle and consequent loading.

(2) Meridional flow analysis to determine the shapes of the surfaces of revolution

and the distribution of the meridional velocity cs.

The geometrical content of item (1) will be dealt with next, followed in Section

7.5 by an initial consideration of the fluid flow aspects of mixed-flow cascades. Full

details of a theoretical fluid-dynamic design and analysis method for mixed-flow

cascades have been given by the author elsewhere (Lewis, 1991). This technique

is based on boundary integral modelling by the surface vorticity method, the

foundations of which are developed in Chapter 9 for aerofoils and cascades and

also for axisymmetric flows past bodies and ducts. Regarding item (2), some

important fundamentals and governing equations for meridional flow have already

been given in Chapters 5 and 6.

7.4 Geometrical techniques for dealing with design and analysis

197

7.4.1 Conformal transformation of a mixed-flow cascade into an equivalent

straight cascade

Figure 7.13 illustrates the transformation of a typical meridional stream surface of

revolution (in the z-plane) into an infinite straight cascade (in the ~'-plane) for the

case of a mixed-flow fan or pump. The equivalent axes in the two planes are as

follows:

(1) Distance s measured along the meridional streamline from some datum P in

the z-plane is equivalent to coordinate ~ in the ~'-plane.

(2) Circumferential distance

rO

is equivalent to coordinate r/.

If the complex variable ~" = ~ + it/is an analytic function ~" =

f(z)

of the complex

variable

z = s + irO,

not only the blade geometry but also the flow field in the z-plane

may be transformed across to the ~'-plane or vice versa. The reader is referred to

advanced fluid-dynamics texts such as Batchelor (1970) for a full treatment of

conformal transformation. For the present purpose the condition of conformality may

be described quite simply by reference to the two equivalent elementary areas ds.

rdO

and d~. dr/shown in Fig. 7.13. For the transformation to be

conformal

these elements

must be geometrically similar, that is

(1) The corner angles should be the same.

(2) Equivalent sides (such as ds and d~: or

rdO

and dr/) should bear a fixed ratio.

In both planes all corner angles are 7r/2 satisfying condition (1). Condition (2) may

be stated as follows:

d~ ds

dr/ rdO

(for conformality) (7.30)

Following Young (1958), this may be achieved by the separate coordinate transforma-

tions

ds

d~=m=

/,

dr/= dO

1dr}

r sin 3' (7.31)

where 3, = sin-l(dr/ds) is the local cone angle of the meridional streamline, Fig. 7.13.

Integration of these equations gives us the direct coordinate transformations:

f lds I 1 dr t

sc = r r sin 7 (7.32)

r/=O

From the second of these equations it is clear that the mixed-flow cascade of say Z

blades transforms into an infinite straight cascade in the ~" plane stretching between

?7 = +o0 and of pitch

2ql"

t =~ (7.33)

Z

198

Mixed-flow and radial turbomachines

Equation (7.32a) may be integrated numerically if y is specified as a function of r.

On the other hand for true conical surfaces with angle 3' = constant, Eqn (7.32)

becomes

1 In(r) }

s~ = sin y

,1=0

(7.34)

7.4.2 Pitch/chord ratio and stagger of a mixed-flow cascade

At first sight the awkward geometry of a mixed-flow cascade would seem to rule out

the definition of representative pitch/chord ratio and stagger, Fig. 7.13(a). This

problem is resolved by the transformation method. Thus in the transformed ~'-plane,

Fig. 7.13(b), the blade chord is given by l = (s~2 - S~l)/CosA, and making use also of

Eqn (7.33), the pitch/chord ratio becomes

t _ 27r cos A

l Z(sr2-

~1)

_

2~r cos A sin y

Zln(r2/rl)

(7.35)

The stagger angle A can be calculated from the given leading and trailing edge

coordinates of the mixed-flow blade row (rl, 01) and (rE, 02) by reference again to the

transformed cascade in the ~'-plane:

7/2 -- '01 (02 -- 01)sin

y

tanA = ~2- ~1

ln(r2/rl)

(7.36)

Example 7.2

Problem

Calculate A and

t/l

for a mixed-flow cascade given the following data, as in Fig.

7.13"

Number of blades Z = 8, y = 30 ~

r 1 =

50 mm 01 = 0

r2 = 75 mm 02 = 45 ~

(leading edge coordinates)

(trailing edge coordinates)

Solution

From Eqn (7.36)

From Eqn (7.35)

A = tan-11

71"

45 •

180

x sin 30 ~

In (75/50)

= 44.084 ~

t

- = 0.6957

l

7.4 Geometrical techniques for dealing with design and analysis

199

7.4.3 Axial and radial blade rows

Axial and radial blade rows are special cases of the mixed-flow cascade for which

the cone angle y is equal to zero and zr/2 respectively.

Axial blade rows

Thus for an axial blade row, since the stream surface is cylindrical, r = constant, the

transformation Eqns (7.32) reduce to

x (rO)

~: = -, r/= (7.37)

r r

As illustrated by Fig. 2.2 and discussed already in Chapter 2, this is equivalent to

simply unwrapping and flattening out the cylindrical meridional surface, generating

identical blade profile geometry in the r

Radial guide vanes

For radial cascades, on the other hand, Eqns (7.34) are applicable and setting 3' = 7r/2

we obtain

s c = In (r), r/= 0 (7.38)

The analytical relationship between the complex coordinates ~" =

f(z)

may now be

determined since

~"

= r + it/= In r + i0 = In (r

e i~

(7.39)

= lnz

which is a very well-known conformal transformation between Cartesian and polar

coordinate systems.

The application of this log transformation to a straight cascade of turbine blades

is shown in Fig. 7.14. In this case the fluid flows from right to left in the ~'-plane in

order to simulate a set of radial inflow guide vanes such as might be used at entry

to the Francis turbine previously shown in Fig. 7.11. The straight cascade shown here

was designed using the program STACK with a stagger of )t = 45 ~ a circular arc

camber with angle 0 = 30 ~ and pitch/chord ratio

t/l

= 1.0. The circular cascade was

transformed from this by embedding the above coordinate transformations into a

Quattro Pro spreadsheet.

Velocity transformation

For

stator

cascades such as this inlet guide-vane blade row, it is also possible to

transform the complex velocity in the if-plane qc = u~ + iv~ from the straight cascade

to its value

qz = Uz + iVz

at the equivalent point in the z-plane. By introducing the

complex potential to = ~b + iqJ the following general relationship is then applicable

(Batchelor, 1970):

Uz

dw dw d~"

-iVz= dz - d~ dz

d~

=

(7.40)

200

Mixed-flow and radial turbomachines

1.2

0.8

Y

0.4

0.0

-0.4

-0.8

-I.2

.6 -!.2 -0.8 -0.4 0.0 0.4 0.8

X

1.2 1.6

t =

12

.6 -I.2 -0.8 ~l ~

/,

(a) (b)

/

~2Y j

//

J

&_~0o

/

0.4 0.8 ~ 1.2 1.6

Fig.

7.14 Transformation of a set of radial inflow guide vanes into an equivalent straight cascade

(a) radial guide vanes in the z-plane; (b) transformed straight cascade in the ~'-plane

But from Eqn (7.39)

d~/dz = 1/z,

and the last equation then reduces to

1

m

qz=rq~

(7.411

Thus velocities calculated by straight cascade analysis in the ~-plane can be

transformed across to the radial cascade simply scaled by

1/r.

For

rotors,

on the other hand, an allowance must be made for the 'relative rotation ~

in fluid dynamic analyses. This matter is too complex to be dealt with here but ha,.

been discussed in detail by Lewis (1966, 1991) and is handled by the author's software

MIXEQU. The physical nature of the 'relative eddy' or 'slip' flow will be discussed

next.

7.5

Relative eddy and slip flow in radial and mixed-flow

turbomachines

As early as 1928 Busemann published his classic paper on prediction of the flo~

through centrifugal pump rotors with logarithmic spiral blades, using conforma]

transformation theory. It was already fully realised that the flow viewed relative tc

a centrifugal pump or fan is strongly influenced by the so-called 'relative eddy' whict,

is introduced when transforming from stationary coordinates to a system which rotate,

with the rotor. For example, consider the simple radial bladed centrifugal impellel

illustrated in Fig. 7.15.

Let us assume that the flow enters without swirl,

Col

= 0, and is thus irrotational

Fig. 7.15(a). Adopting polar coordinates

(x,r, O)

which are stationary relative to the

laboratory, the vorticity to will be zero. From its definition, Eqn (6.10a), we ther,

have

aCo Co 1

aC r

to= Or "r r r O0 0

(7.421

with the sign convention that both to and the rotor angular velocity 1} are definec

as anticlockwise positive.

7.5 Relative eddy and slip flow in radial and mixed-flow turbomachines

201

+

t0=0

Relative eddy

+

~el = -20

J

c d

(a) (b) (c)

Fig.

7.15 Relative eddy

and slip flow in a radial bladed pump impeller: (a) zero vorticity to in stationary

coordinates; (b) vorticity

Wre I in rotating coordinates and relative eddy; (c) streamline flow relative to

blade passage

abcd

Let us now consider the flow as viewed by an observer sitting on and travelling

with the rotor. The velocity components

(Wr, wo)

relative to his coordinate system

which rotates with the rotor are related to those in the stationary coordinates

(Cr, Co)

through Eqns (7.10b) and (7.10c). Introducing these into Eqns (7.42) results in the

following expression for the relative vorticity tore I as seen by the observer:

OWo Wo lo3w

r

tOrel

=

O-r--- -k- r r O0 -- -- 21~ (7.43)

Thus viewed relative to the rotor the entire flow field is filled with vorticity tore I

Of

strength 213, i.e. double the rotor angular velocity fl but clockwise in direction.

Because of this, the packet of fluid contained within any blade passage such as

abcd,

Fig. 7.15(b), being temporarily cut off from fluid in neighbouring blade passages,

tends to rotate in the clockwise sense as illustrated, producing the slip velocity W0s

along the exit line

cd.

Superimposing the throughflow on top of this the streamline

pattern of the relative flow will be similar to that illustrated in Fig. 7.15(c). Instead

of leaving radially parallel to the blades, the flow slips backwards in the direction

opposite to rotation, resulting in a reduction in the anticipated head rise. To account

for this the slip factor may be defined as follows:

Actual swirl velocity at rotor exit c02

tr = (7.44)

Swirl velocity with perfect guidance by the blades c~2

where cb2 is based on the ideal machine in which the relative flow at exit follows

the blade direction exactly. Thus for radially bladed machines cb2 = U2 = r213 and

the slip factor becomes

U 2 -- WOs WOs

or= = 1 (7.45)

U2 U2

The slip factor will thus always be less than unity and provides a simple basis for

implementing the relative eddy slip flow correction. Thus from the Euler pump

equation (7.1) the predicted frictionless head rise becomes

ho2- hol =

U2c02 = orU2c'02

(7.46)

where c~2 assumes

perfect guidance by the blades

at exit from the rotor.

202

Mixed-flow and radial turbomachines

/~ S////~~// 1.0 t/l = 0.5

!.0

1.5

0.8 2.0

O"

0.6

0.4

ltZ

Lewis 9 30 blades

0.2

9 20 blades

-- ~ Stanitz 0.0

0.0 0.2 0.4 0.6 0.8 1.0

rl/r2

(a) (b)

Fig. 7,16 Typical streamline pattern for a radial bladed centrifugal impeller and

predictions of slip factor

for a wide range of geometries

and blade numbers: (a) streamline pattern with 20 blades; (b) slip

factors

for range of geometries

7.5.1 Predicted slip factors for radial bladed centrifugal machines

Theoretical analyses of radial bladed rotors were undertaken by Stanitz (1952) using

finite difference methods and by Lewis (1966) by conformal transformations, both

methods permitting the prediction of streamline patterns. Results are compared in

Fig. 7.16 for a 20-bladed rotor with radius ratio

rl/r2

= 0.65. Stanitz imposed a

boundary condition of radial entry flow at rl. Lewis's method, on the other hand,

modelled the entry flow also and Fig. 7.16(a) shows the predicted flow with prewhirl

put equal to the blade speed,

col

= rlf~. The methods are in good agreement and

reveal strong slip flow at the rotor exit. Predicted slip factors according to Lewis's

theory are compared with the results of Busemann (1928) in Fig. 7.16(b) for a very

wide range of radial bladed impellers but with zero prewhirl,

col

= 0, showing

excellent agreement. Two cases calculated by Stanitz are also shown and are found

to be in good agreement. Although Stanitz assumed the presence of prewhirl

col

--

r 1

~

for these cases, the blades are sufficiently tightly packed for the entry flow

at rl to exercise almost insignificant influence over the exit flow at r2.

Of special interest in relation to this last point are the contours of constant

pitch/chord ratio superimposed upon Fig. 7.16(b). These were obtained from Eqn

(7.35), introducing y = zr (for radial meridional flow) and A = 0 (zero stagger for

radial blades). For

t/l

< 1.0 the slip factor or is almost constant for a given number

of blades as

rl/r2

is reduced. For

t/l

> 1.0, on the other hand, the slip factor falls off

considerably as either (a) the number of blades is reduced or (b)

rl/r2

is increased.

This behaviour pattern is much in line with that of axial cascades as discussed in

Chapter 4, Section 4.8 in relation to fans. As a general rule it is advisable to select

the blade number Z and the radius ratio

rl/r2

such that

t/l

< 1.0 in order to maintain

high slip factors and thus high head rise. For radial bladed machines this design

constraint can be fed into Eqn (7.36) to give recommended minimum blade numbers,

namely

277"

Z > (for

t/l

< 1.0) (7.47)

ln(r2/rl)

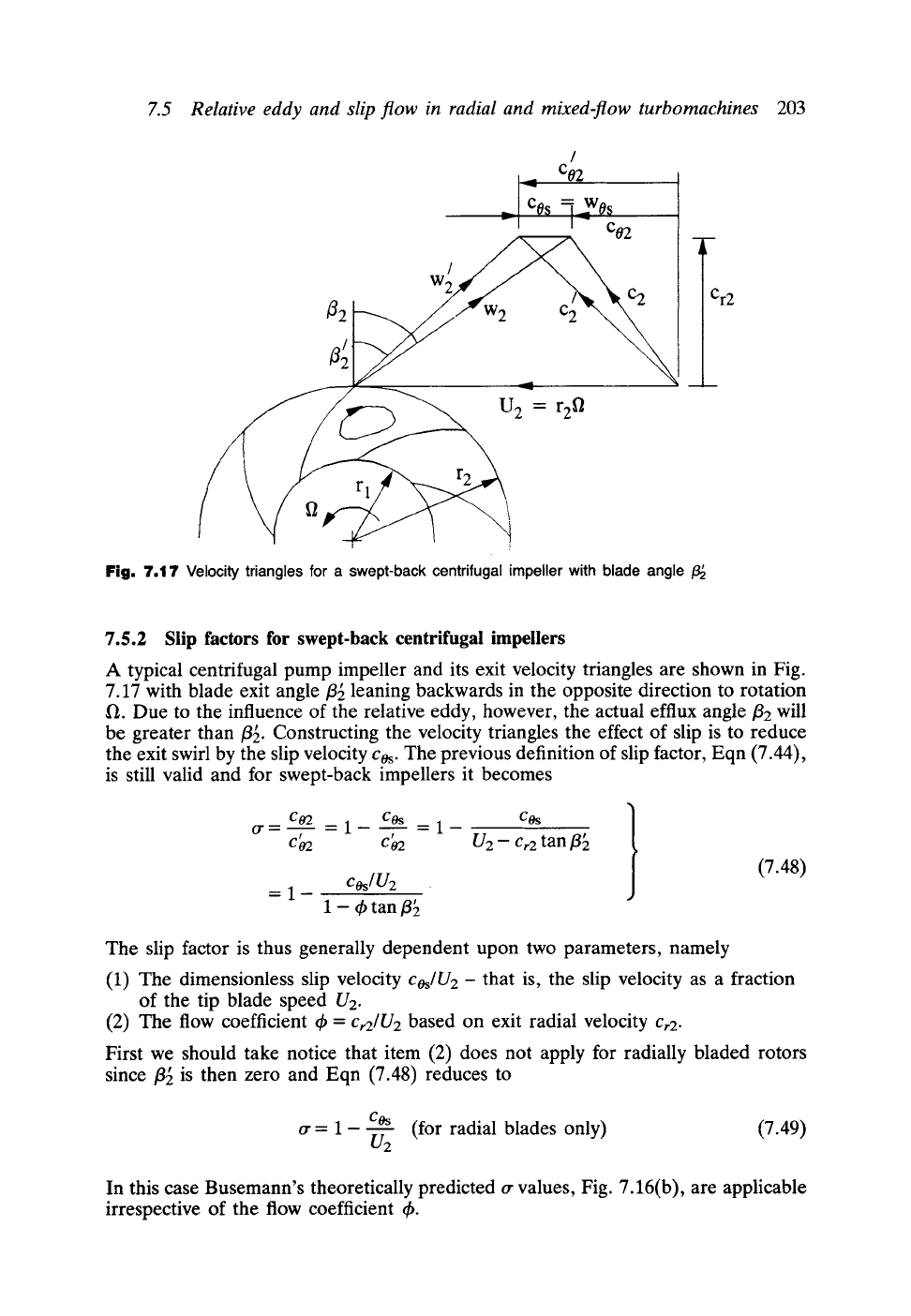
7.5 Relative eddy and slip flow in radial and mixed-flow turbomachines

203

/

C02

_lcos Wos

"--I I--"

C0 2

/

_ m

Cr2

Fig. 7.17 Velocity

triangles for

a swept-back centrifugal impeller with blade angle

7.5.2 Slip factors for swept-back centrifugal impellers

A typical centrifugal pump impeller and its exit velocity triangles are shown in Fig.

7.17 with blade exit angle/3~ leaning backwards in the opposite direction to rotation

II. Due to the influence of the relative eddy, however, the actual efflux angle/32 will

be greater than/3~. Constructing the velocity triangles the effect of slip is to reduce

the exit swirl by the slip velocity cos. The previous definition of slip factor, Eqn (7.44),

is still valid and for swept-back impellers it becomes

C02 COs COs

or= =1 =l-

CP02 Ct02 U 2 - Cr2

tan/3~

=1-

co/U2

1 - 4' tan 13[

(7.48)

The slip factor is thus generally dependent upon two parameters, namely

(1) The dimensionless slip velocity

cOs~U2-

that is, the slip velocity as a fraction

of the tip blade speed U2.

(2) The flow coefficient th =

Cr2/U2

based on exit radial velocity

Cr2.

First we should take notice that item (2) does not apply for radially bladed rotors

since/3~ is then zero and Eqn (7.48) reduces to

COs

tr = 1--77", (for radial blades only) (7.49)

u2

In this case Busemann's theoretically predicted or values, Fig. 7.16(b), are applicable

irrespective of the flow coefficient 4,.

Lewis R.I. Turbomachinery Performance Analysis

Подождите немного. Документ загружается.