Lewis R.I. Turbomachinery Performance Analysis

Подождите немного. Документ загружается.

Viability

check

Overall duty

Specification

Dimensional analysis

Choice of machine type

and number of stages

- l

FIPSI

Thermo-fluid dynamic design

Annulus shape

Centre-line design

Velocity triangles

-f

Meridional

Analysis

Annulus and

secondary losses

I L

Blade design

" Blade-to-blade

"- I cascade design

Profile stacking

Stress & vibration

Anal~,sis

Assemble design data [

Fig. 1.2 Overall design sequence for a multi-stage axial turbine

CASCADE

STACK

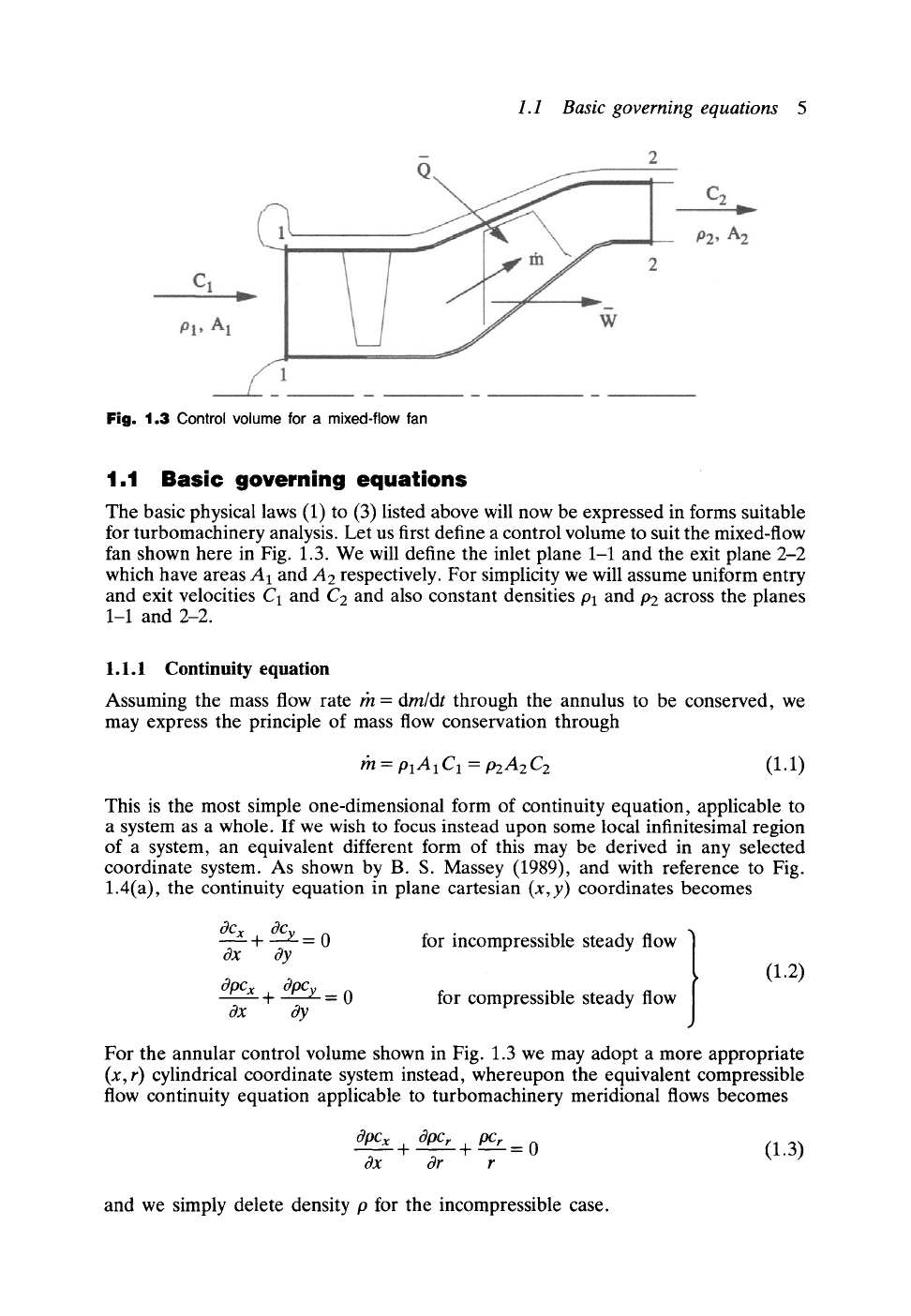
1.1 Basic governing equations 5

Fig.

1.3 Control volume for a mixed-flow fan

1.1 Basic governing equations

The basic physical laws (1) to (3) listed above will now be expressed in forms suitable

for turbomachinery analysis. Let us first define a control volume to suit the mixed-flow

fan shown here in Fig. 1.3. We will define the inlet plane 1-1 and the exit plane 2-2

which have areas A1 and A2 respectively. For simplicity we will assume uniform entry

and exit velocities

C 1

and C2 and also constant densities/91 and Pa across the planes

1-1 and 2-2.

I.I.I Continuity equation

Assuming the mass flow rate rh =

dm/dt

through the annulus to be conserved, we

may express the principle of mass flow conservation through

tn = plA1C 1 ~- p2A2C 2

(1.1)

This is the most simple one-dimensional form of continuity equation, applicable to

a system as a whole. If we wish to focus instead upon some local infinitesimal region

of a system, an equivalent different form of this may be derived in any selected

coordinate system. As shown by B. S. Massey (1989), and with reference to Fig.

1.4(a), the continuity equation in plane cartesian

(x,y)

coordinates becomes

acx acy

t- =o

Ox ay

0OCx 0OCy

0x 0y

for incompressible steady flow

for compressible steady flow

(1.2)

For the annular control volume shown in Fig. 1.3 we may adopt a more appropriate

(x,r)

cylindrical coordinate system instead, whereupon the equivalent compressible

flow continuity equation applicable to turbomachinery meridional flows becomes

03pCx ~pc r [3~r

~-t- .... + ..... 0 (1.3)

Ox Or r

and we simply delete density p for the incompressible case.

6 Basic equations and dimensional analysis

Fig. 1.4 Fluid elements in plane and axisymmetric flow: (a) plane flow in

(x,y)

cartesian coordinates;

(b) axisymmetric flow in (x,r) cylindrical coordinates

1.1.2 Steady flow energy equation

If the First Law of Thermodynamics is applied to the control volume defined in Fig.

1.3 (Rogers and Mayhcw, 1992), we obtain the steady flow energy equation,

- W : rh {(h2 - hi)

+ 1(c2 - c 2) + g(z2 -

Z1)} (1.4)

where Q =

dQ/dt

is the rate of heat supply (if any) to the control volume and

(,V = dW/dt

is the power extracted, h is the specific enthalpy and z the height of the

duct in the gravitational field g. Ignoring the latter potential energy effects for our

axisymmetric case, Fig. 1.3, the steady flow energy equation becomes

-- -- 1 2

Q - W

= (h 2

+ ~C2) --

(h 1 + lc~1 ) = ho2 hol

for compressible flow (1.5a)

12 12

-- (pE/fl "+"

~C2) --

(pl/fl "k-

~Cl) --

PoE-Pol for incompressible flow (1.5b)

where we have divided throughout by rh to obtain the specific (i.e. per unit mass)

values of heat supply Q and work extraction W. ho is called the 'stagnation specific

enthalpy', or 'stagnation enthalpy' for short, and Po is called the 'stagnation

pressure'.

1.1.3 Momentum equation - Euler pump and Euler turbine equations

Instead of the full control volume of Fig. 1.3 we consider next the flow of fluid through

the elementary stream tube q'0 passing through the pump rotor between stations 1

and 2, Fig. 1.5. The torque z which must be supplied through the shaft to the rotor

in order to change the tangential momentum of mass m of fluid from

mcol

mco2

may be found by applying Newton's second law to the elementary control volume,

Fig. 1.5(b). This must take the relevant form for a rotating system, namely

Applied torque = rate of change of moment of momentum

1.1 Basic governing equations 7

Fig. 1.5 Meridional flow through a turbomachine and flow through an elementary streamtube: (a)

meridional flow through a pump or fan rotor; (b) streamtube flowing along the surface of revolution

mapped out by the meridional streamline $o

or expressed analytically,

-r=

--~(mrco)

= rh(r2c02- rlcol)

(1.6)

The power input P then follows directly through

= rhl~(reco2 - rico1)

"-" ?fvl(U2co 2 -- UlCol )

(1.7)

where l~ is the rotor angular velocity and U = r12 is the so-called 'blade speed'. If

we divide through by rh we obtain the specific work input W:

dw/dm

~r = ~ = U 2 c02 - U 1 col (1.8)

Making use of the steady flow en_ergy equation (1.5) and neglecting the heat transfer

rate into the control volume, i.e. Q = 0, we obtain finally the well-known Euler pump

equation for fans with compressible fluids:

ho2 --

hol

-- U2 c02 - U1 col for

compressible

flow

(1.9a)

For incompressible fluids, i.e. liquids or low Mach number gases, we may follow

the same analysis through, using the incompressible steady flow energy equation

instead, namely

0 -- Vr = (P2 - Pl)/P + ( c2 - c2)/2

[1.5bl

8 Basic equations and dimensional analysis

to obtain the corresponding form of the Euler pump equation, namely

(Po2-Pol)/P = U2co2- U1 col for incompressible flow (1.9b)

where Po = P + -~ is the stagnation pressure.

For a turbine rotor we simply reverse suffices 1 and 2 to obtain the Euler turbine

equation, namely

hol - ho2 = UlCol - U2co2 for compressible flow } (1.10)

(Pol-Po2)/P = UlCol- U2co2 for incompressible flow

The Euler pump and turbine equations as derived here are one-dimensional

equations in the sense that they are applicable to unit mass of fluid flowing along the

line mapped out by the elementary streamtube illustrated in Fig. 1.5(b). The

circumferential projection of such infinitely thin stream tubes onto the (x, r) plane

leads to the definition of a family of so-called meridional streamlines illustrated in Fig.

1.5(a) of which the hub and casing form the boundary streamlines. It is clear that one

Euler pump or turbine equation must be derived for each meridional streamline

during the design phase for a turbomachine and that these equations will lead to a

precise specification of the swirl velocity change from col to c02 required for a specified

stagnation enthalpy change

hol to ho2.

The Euler pump or turbine equation is thus

central to the design process, combining both the energy and momentum conservation

laws, and will be referred to many times throughout this book.

As with the continuity equation treatment in Section 1.1.1 above, it is possible and

indeed necessary for detailed flow modelling to derive differential equations

equivalent to the one-dimensional equations of this section in order to express the

three-dimensional or more frequently two-dimensional axisymmetric equations of

motion at any point in a turbomachine. It will be more helpful to leave this matter

for fuller consideration in Chapters 6 and 7 where we will show how such equations

may be used to derive the actual meridional streamline distributions such as that

illustrated in Fig. 1.5(a).

All of the basic governing equations required for the time being have now been

derived. Further consideration will be given to the second law of thermodynamics

in later chapters as needs demand. To conclude this chapter we will now give some

preliminary consideration to dimensionless groups of special significance to the

turbomachinery designer.

1.2 Dimensional analysis

An indication of the primary goals of dimensional analysis was given in the

introduction to this chapter. In the present section attention will be drawn to two

different levels of dimensional analysis and consequent dimensionless groups,

namely

(a) global dimensionless performance variables, artd

(b) local dimensionless design and performance variables.

The first of these may be more familiar to the student and is concerned with the key

overall or global performance variables of a turbomachine such as flow rate, pressure

rise and efficiency in the case of a fan or pump. Such global dimensionless groups

will be derived in Section 1.2.1 to illustrate the power and scope of dimensional

analysis to take advantage of laboratory-scale model testing as a design and

1.2 Dimensional analysis 9

performance predictive tool. An extension of the use of global dimensionless variables

for the selection of machine type, axial, radial or mixed-flow, to best suit a given

operating duty specification will be outlined in Section 1.2.2 with reference to useful

published correlations.

The use of local dimensionless variables may be less familiar territory for the

student and is the main theme of many of the subsequent chapters of this book where

analytical developments will be laid out in detail for a wide range of turbomachine

types. In view of this a brief outline only will be given in Section 1.2.3 to illustrate

the main ideas and implications of this type of analysis, which involves selection of

dimensionless performance coefficients for each meridional streamline such as ~0,

Fig. 1.5.

1.2.1 Overall dimensional analysis and

global

dimensionless performance

parameters

The fundamental basis of dimensional analysis is well covered in standard fluid-

dynamic texts such as Massey (1989) or Shepherd (1965), including the use of

Buckingham's ~r-theorem to derive dimensionless groups, and will be taken as read.

For the present purpose we will approach the matter from the turbomachinery

engineer's viewpoint by considering the performance analysis of a given centrifugal

pump, drawing out its main key performance characteristics and showing how global

dimensionless performance parameters can help to take advantage of scale model

tests.

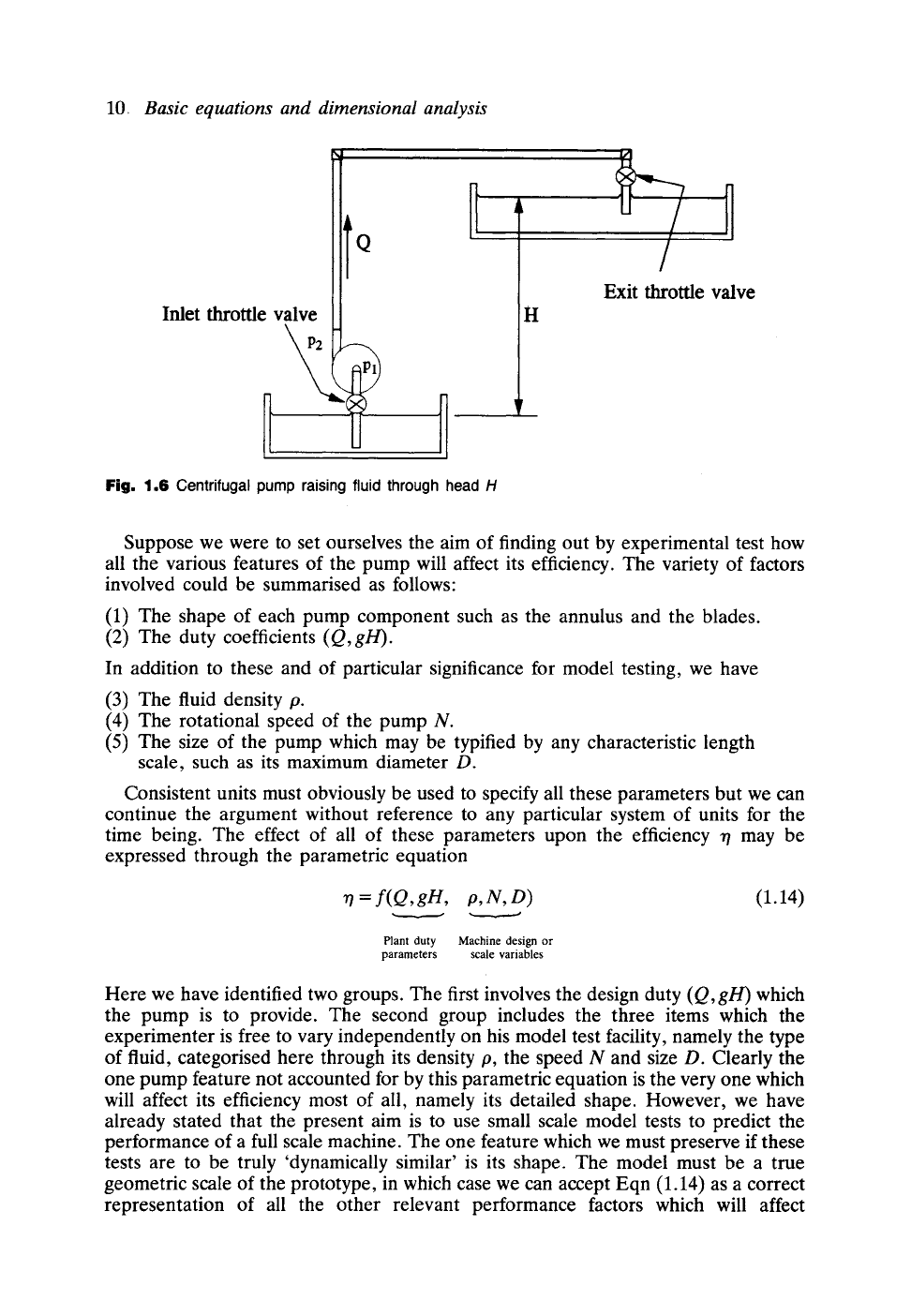
For example, let us consider the twofold purpose of the centrifugal pump illustrated

in Fig. 1.6, namely

(a) to move fluid at a specified flow rate Q, and

(b) to raise the fluid pressure through

(P2--Pl),

achieving both goals with high pumping efficiency r/. Alternatively we may regard

the second duty requirement (b) as that of lifting the fluid through the height H in

the gravitational field g, where Bernouilli's equation or the incompressible steady

flow energy equation (1.5b) provides the connecting relationship

P2 -- Pl = pgH (1.11)

The effective 'pumping power' P (i.e. the useful power output of the pump) may

then be calculated through

P = rhgH = pQgH (1.12)

where rh is the mass flow rate and p the fluid density. In other words, the pumping

power delivered is the product of the two specified primary design duty parameters

(Q,gH) and is also proportional to g and p. The quantity gH is in fact the energy

input to a unit mass of fluid passing through the pump and turns out to be a more

useful parameter than simply H in subsequent dimensional analysis. We will term

it the gravitational head. A suitable definition of overall hydraulic efficiency then

follows from

Pumping power

7/= Shaft input power

pQgH

where ~-is the shaft input torque and N the rotational speed.

(1.13)

10 Basic equations and dimensional analysis

Inlet throttle

valve

Fig. 1.6 Centrifugal pump raising fluid through head H

Exit throttle

valve

Suppose we were to set ourselves the aim of finding out by experimental test how

all the various features of the pump will affect its efficiency. The variety of factors

involved could be summarised as follows"

(1) The shape of each pump component such as the annulus and the blades.

(2) The duty coefficients (Q,gH).

In addition to these and of particular significance for model testing, we have

(3) The fluid density p.

(4) The rotational speed of the pump N.

(5) The size of the pump which may be typified by any characteristic length

scale, such as its maximum diameter D.

Consistent units must obviously be used to specify all these parameters but we can

continue the argument without reference to any particular system of units for the

time being. The effect of all of these parameters upon the efficiency r/ may be

expressed through the parametric equation

7q= f(Q, gH, p,N,D) (1.14)

Plant duty Machine design or

parameters scale variables

Here we have identified two groups. The first involves the design duty (Q, gH) which

the pump is to provide. The second group includes the three items which the

experimenter is free to vary independently on his model test facility, namely the type

of fluid, categorised here through its density p, the speed N and size D. Clearly the

one pump feature not accounted for by this parametric equation is the very one which

will affect its efficiency most of all, namely its detailed shape. However, we have

already stated that the present aim is to use small scale model tests to predict the

performance of a full scale machine. The one feature which we must preserve if these

tests are to be truly 'dynamically similar' is its shape. The model must be a true

geometric scale of the prototype, in which case we can accept Eqn (1.14) as a correct

representation of all the other relevant performance factors which will affect

1.2 Dimensional analysis 11

efficiency. There could of course be other influential factors such as the fluid viscosity

but we will ignore these for the moment just to keep the argument simple.

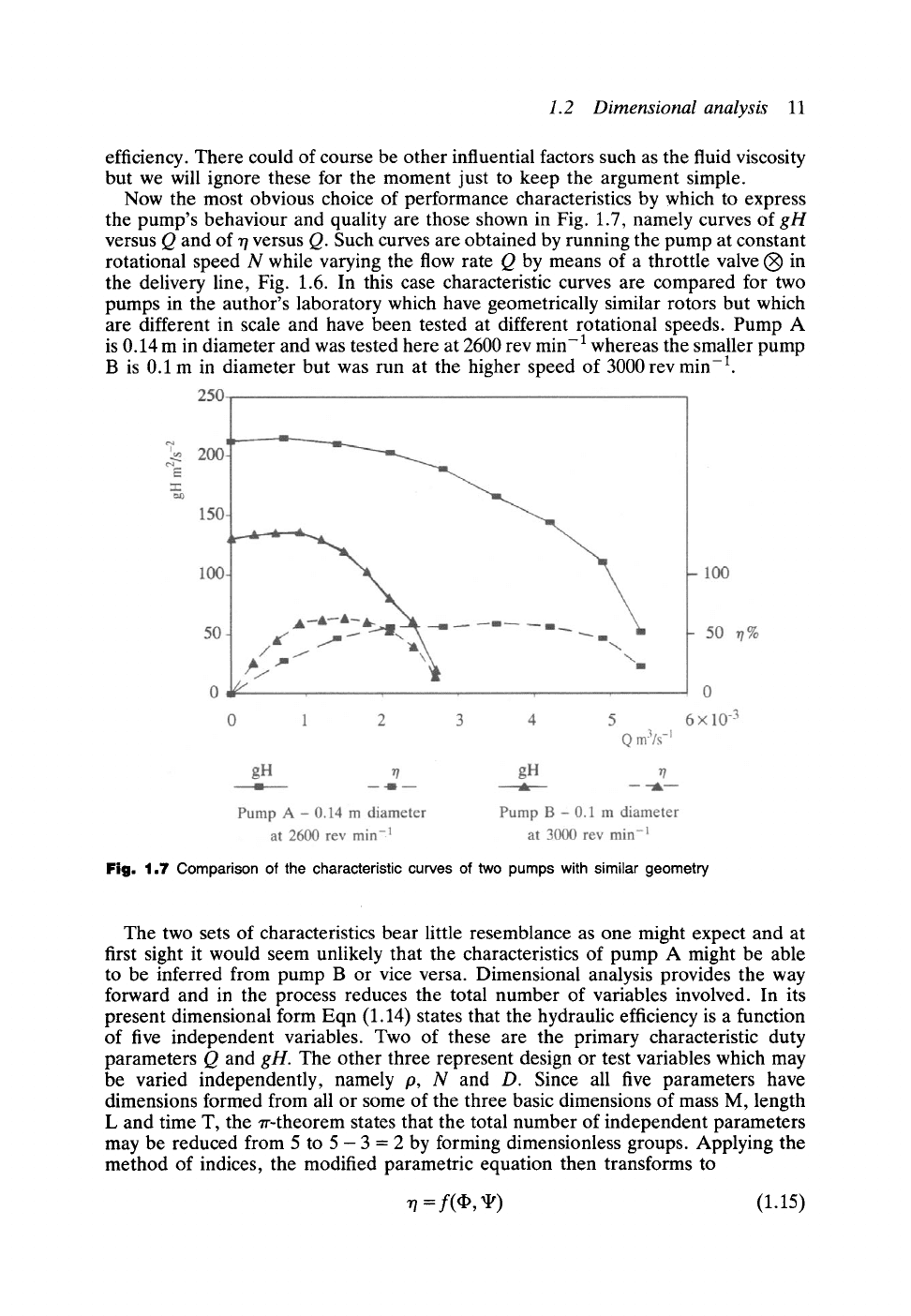
Now the most obvious choice of performance characteristics by which to express

the pump's behaviour and quality are those shown in Fig. 1.7, namely curves of

versus Q and of r/versus Q. Such curves are obtained by running the pump at constant

rotational speed N while varying the flow rate Q by means of a throttle valve (~) in

the delivery line, Fig. 1.6. In this case characteristic curves are compared for two

pumps in the author's laboratory which have geometrically similar rotors but which

are different in scale and have been tested at different rotational speeds. Pump A

is 0.14 m in diameter and was tested here at 2600 rev min -1 whereas the smaller pump

B is 0.1 m in diameter but was run at the higher speed of 3000 rev min -1.

Fig, 1,7 Comparison of the characteristic curves of two pumps with similar geometry

The two sets of characteristics bear little resemblance as one might expect and at

first sight it would seem unlikely that the characteristics of pump A might be able

to be inferred from pump B or vice versa. Dimensional analysis provides the way

forward and in the process reduces the total number of variables involved. In its

present dimensional form Eqn (1.14) states that the hydraulic efficiency is a function

of five independent variables. Two of these are the primary characteristic duty

parameters Q and

gH.

The other three represent design or test variables which may

be varied independently, namely p, N and D. Since all five parameters have

dimensions formed from all or some of the three basic dimensions of mass M, length

L and time T, the zr-theorem states that the total number of independent parameters

may be reduced from 5 to 5- 3 = 2 by forming dimensionless groups. Applying the

method of indices, the modified parametric equation then transforms to

= f(q~, ~) (1.15)

Basic equations and dimensional analysis

where the dimensionless global duty parameters are as follows"

dp = Q/(ND 3)

Flow coefficient }

= gH/(N2D 2)

Head coefficient (1.16)

The efficiency is thus dependent upon only two dimensionless parameters which

represent the primary duty requirements of the pump, namely the production of flow

and head rise ~.

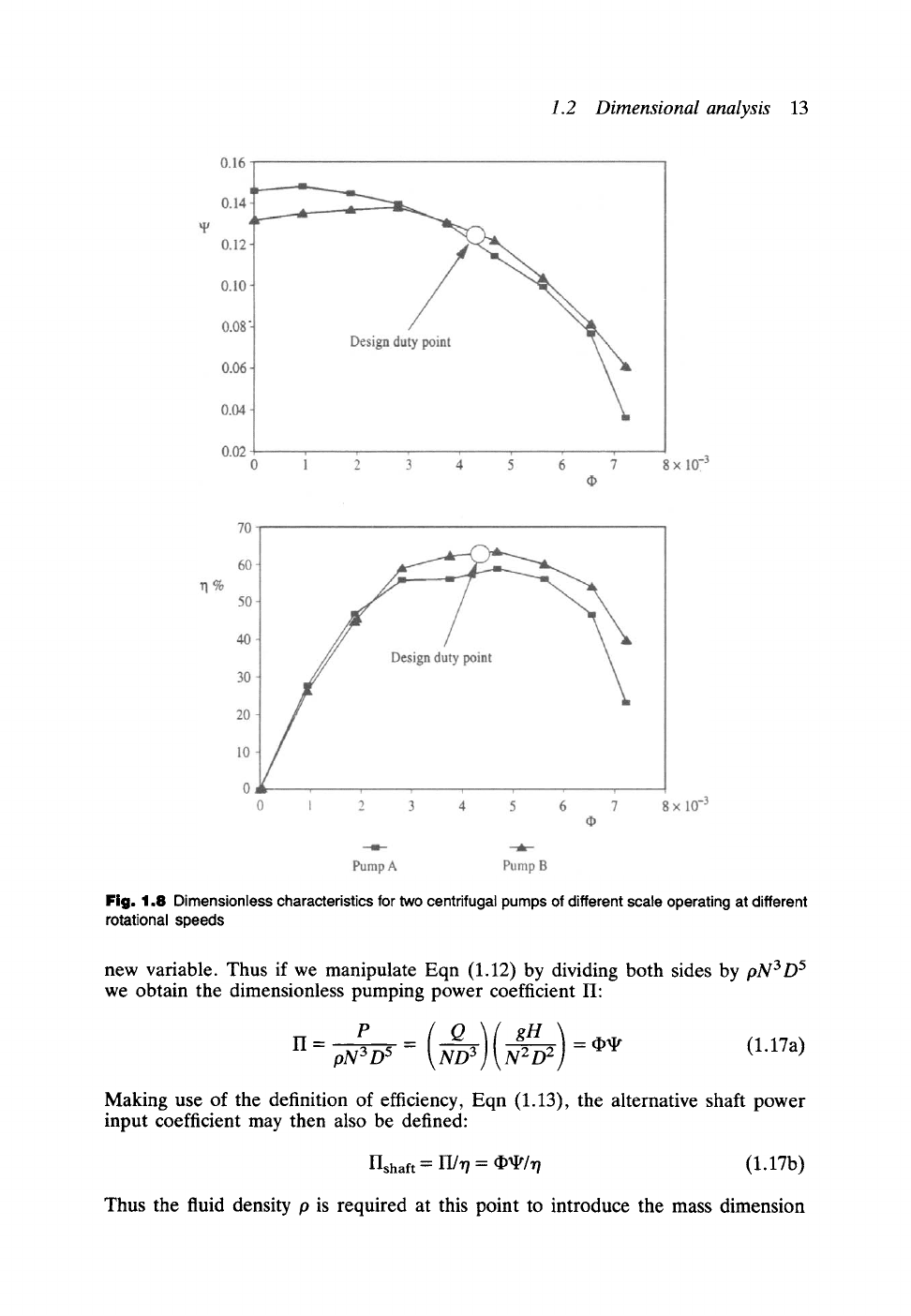
If the test data for the two pumps previously considered are replotted as ~-~ and

rt--~ characteristics instead, as shown in Fig. 1.8, they are found to be remarkably

similar to one another, bearing in mind of course that although the overall blade and

annulus geometries are generally true to scale, there will be differences of surface

finish and more importantly of tip clearance between blade and casing, a parameter

which is difficult to set precisely. Despite these minor departures from true

geometrical similarity, both the head and efficiency characteristics follow the same

pattern over a wide range of operating duties. Thus we may conclude from this study

that one set of scale model test results would have been sufficient to predict the actual

characteristic of both pumps and, if required, for a very much larger prototype,

resulting in a considerable reduction in effort and cost. Furthermore from the

dimensionless characteristics we may select a recommended design duty point (~

located somewhere close to the maximum efficiency.

It is essential to use a consistent set of units for D, N, Q, g and H when evaluating

and ~. All consistent sets will then deliver the same values for these truly

dimensionless coefficients. We will adopt the SI system for which the dimensions and

units of various useful quantities are summarised in Table 1.1.

The reader may have noticed that the fluid density p does not as yet feature in

the dimensionless coefficients, Eqn (1.16), since it is the only one of the five variables

in Eqn (1.14) to include the mass dimension M. It is normal practice, however, to

plot a third dimensionless characteristic to express power P versus flow Q. According

to the 7r-theorem any pair of dimensionless variables may be combined to form a

Table 1.1 Quantities and their dimensions and SI units

Quantity Dimension Unit Symbol or

combination

Length L metre m

Mass M kilogram kg

Time interval T second s

Velocity LT- 1 metres per second m s- 1

Force MLT -2 newton N or kg m s -2

Pressure ML-1T -2 pascal Pa or N m -2

Work, heat ML2T -2 joule J or N m

Power ML2T -3 watt W or J s -1

Rotational speed T-1 radians per second rad s-1

Frequency T- 1 hertz Hz or s- 1

Density p ML -3 kilograms per metre 3 kg m -3

Dynamic viscosity/z ML-1T- 1 poise kg m-1 s-1

Kinematic viscosity v L2T - 1 stoke - 10 -4 m 2 s- 1 m 2 s- 1

1.2 Dimensional analysis

Fig. 1.8 Dimensionless characteristics for two centrifugal pumps of different scale operating at different

rotational speeds

new variable. Thus if we manipulate Eqn (1.12) by dividing both sides by

pN3D 5

we obtain the dimensionless pumping power coefficient II"

rl = pN3D 5 = ND 3 N2D2

= ~ (1.17a)

Making use of the definition of efficiency, Eqn (1.13), the alternative shaft power

input coefficient may then also be defined:

Ilshaf t = II/r/= (I)xP'/r/

(1.17b)

Thus the fluid density p is required at this point to introduce the mass dimension