Lewis R.I. Turbomachinery Performance Analysis

24

Two-dimensional cascades

Blade No. 1

S-]

surfaces

S-2 surfaces

I

r

Fig. 2.4

S-1 and S-2 stream surface (after Wu, 1952)

Blade No. 2

codes. Crucial though this is for advancement of the thermo-fluid dynamic design

of turbomachines, detailed review is beyond the scope of this book. Much more

simplified meridional flow analysis treatments will be given in Chapter 5, followed

in Chapter 6 by a detailed discussion of the mechanisms of vorticity production in

turbomachines and their influence upon meridional flows.

In Section 2.1 we will develop the overall fluid dynamic analysis of two-dimensional

compressor and fan cascades including the definition of key performance parameters.

Section 2.2 will be concerned with the efficiency of a compressor cascade viewed as

a diffuser. Design and analysis of cascades by direct and inverse methods will be

discussed in Sections 2.3 to 2.5. Means for selection of optimum cascades will be dealt

with in Sections 2.6 and 2.7. The chapter is concluded with methods for predicting

the fluid deviation or outlet angle in Section 2.8. Illustrative use of the program

CASCADE will be made where relevant and familiarisation of the reader with this

would be helpful. User instructions are given in full in Appendix II.

2.1 Cascade dynamics and parameters

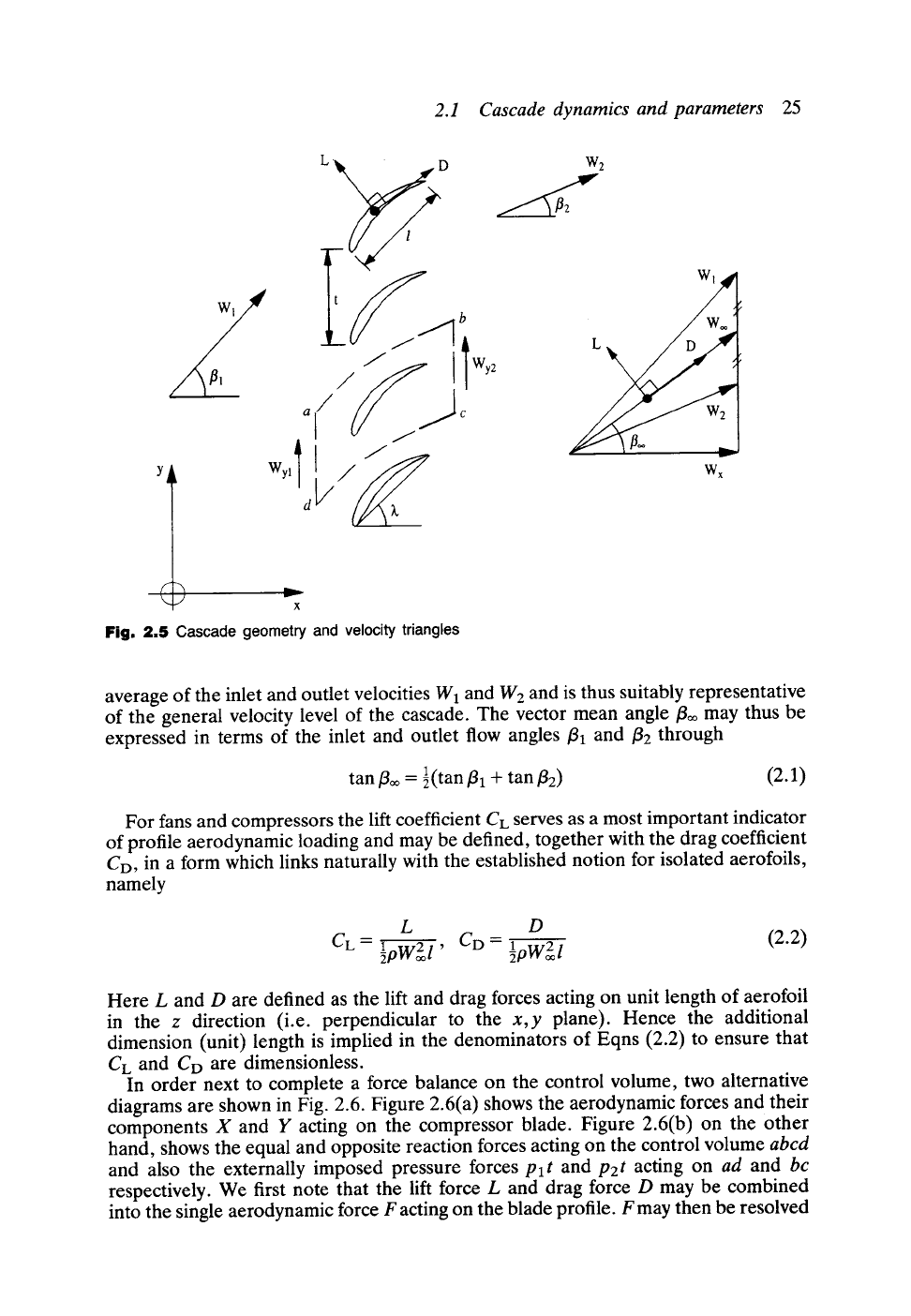
In order to derive equations which express the fluid dynamic effect of a blade row,

let us consider flow through the control volume

abcd

surrounding one blade of a

compressor cascade, Fig. 2.5. Analysis is simplified if we select sides

ab

and

dc

to

coincide with equivalent streamlines through adjacent passages. Sides

ad

and bc will

be drawn parallel to the y axis and equal in length to the blade pitch t. Generally

speaking the fluid passing through the control volume will be deflected through the

angle e

= fll - f12

in reaction to the lift force L. In addition there will be a drag force

D at right angles to this caused by viscous shear stresses at the blade surface, resulting

in an overall loss of stagnation pressure Apo. Subsequent analysis will show that L

and D lie in the directions normal and parallel to the vector mean velocity Woo. As

shown by the velocity triangles for the blade row, Fig. 2.5, Woo is defined as the vector

2.1 Cascade dynamics and parameters

25

L - D

Wl

b

a W 2

Wyl

Wx

d

Wy2

W2

() x

Fig.

2.5 Cascade geometry and velocity triangles

average of the inlet and outlet velocities

W 1

and WE and is thus suitably representative

of the general velocity level of the cascade. The vector mean angle/3o0 may thus be

expressed in terms of the inlet and outlet flow angles fll and/32 through

tan/3~ = l(tan

~1 +

tan ~2)

(2.1)

For fans and compressors the lift coefficient

C L serves

as a most important indicator

of profile aerodynamic loading and may be defined, together with the drag coefficient

CD, in a form which links naturally with the established notion for isolated aerofoils,

namely

L D

Ct =1 2 CD-- 1 2

(2.2)

~pW~

~pW~l ' 1

Here L and D are defined as the lift and drag forces acting on unit length of aerofoil

in the z direction (i.e. perpendicular to the

x,y

plane). Hence the additional

dimension (unit) length is implied in the denominators of Eqns (2.2) to ensure that

CL and CD are dimensionless.

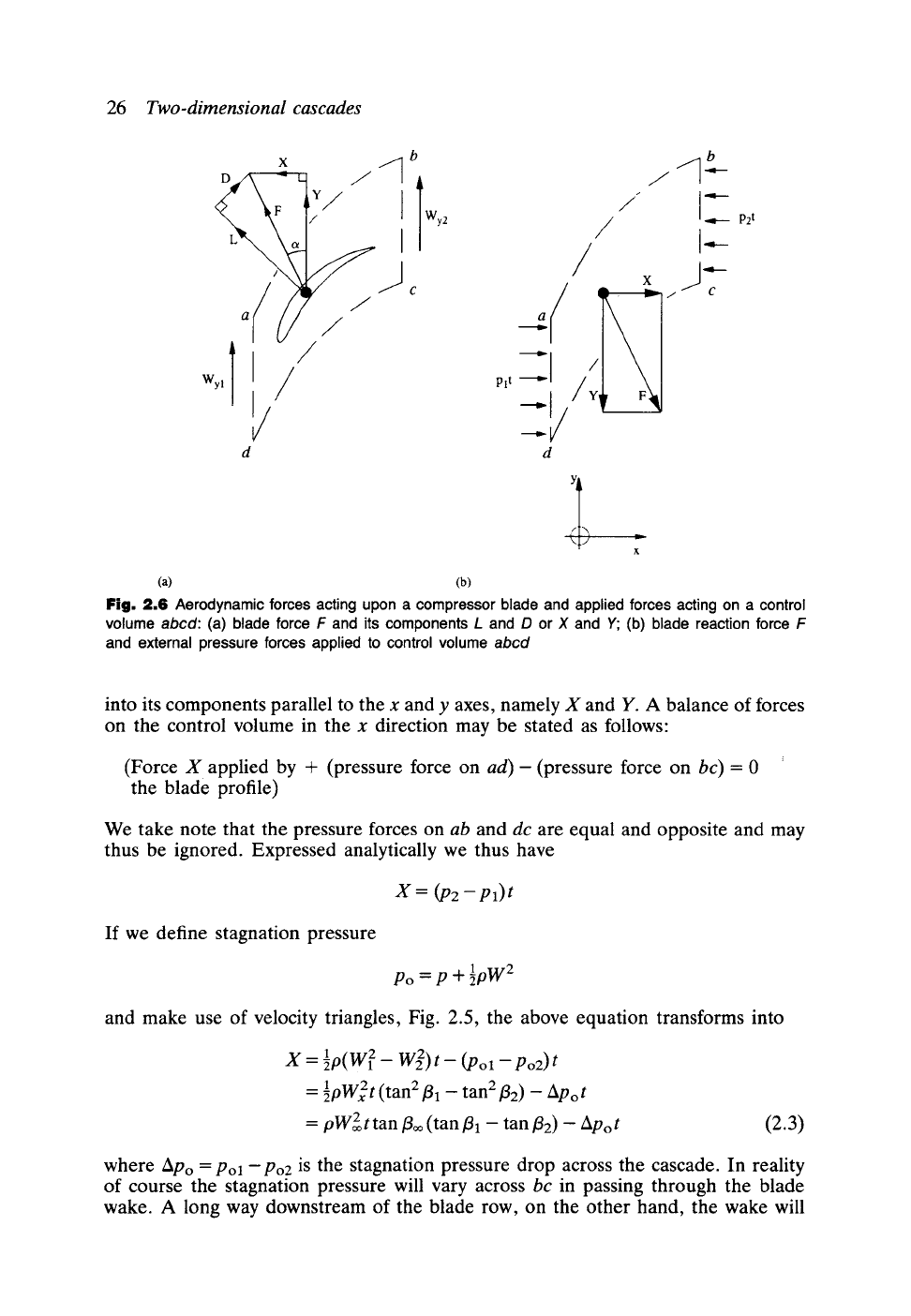
In order next to complete a force balance on the control volume, two alternative

diagrams are shown in Fig. 2.6. Figure 2.6(a) shows the aerodynamic forces and their

components X and Y acting on the compressor blade. Figure 2.6(b) on the other

hand, shows the equal and opposite reaction forces acting on the control volume

abcd

and also the externally imposed pressure forces

pit

and

p2t

acting on

ad

and

bc

respectively. We first note that the lift force L and drag force D may be combined

into the single aerodynamic force F acting on the blade profile. F may then be resolved

26

Two-dimensional cascades

We, l

D x

~~

I

Y

/

d

Wy2

pl t

b

"

I

/ 4--

P2 t

/

/ I--

x ~~-

/

L

,,.[j ,---

X

(a) (b)

Fig. 2.6 Aerodynamic forces acting upon a compressor blade and applied forces acting on a control

volume

abcd:

(a) blade force F and its components L and D or X and Y; (b) blade reaction force F

and external pressure forces applied to control volume

abcd

into its components parallel to the x and y axes, namely X and Y. A balance of forces

on the control volume in the x direction may be stated as follows"

(Force X applied by + (pressure force on

ad)-

(pressure force on

bc)= 0

the blade profile)

We take note that the pressure forces on

ab

and

dc

are equal and opposite and may

thus be ignored. Expressed analytically we thus have

X = (P2 - P 1) t

If we define stagnation pressure

Po = P

+

89 W2

and make use of velocity triangles, Fig. 2.5, the above equation transforms into

X = 89 2 - W2) t (Pol

- Po2) t

1 2

= ~pWx t

(tan 2/31 - tan 2/32) -

Apot

= pW2t

tan/3oo (tan/31 - tan/32) -

Apot

(2.3)

where Apo = Pol-Po2 is the stagnation pressure drop across the cascade. In reality

of course the stagnation pressure will vary across

bc

in passing through the blade

wake. A long way downstream of the blade row, on the other hand, the wake will

2.1 Cascade dynamics and parameters 27

have diffused across the blade pitch t sufficiently for us to regard the flow as uniform,

whereupon the above analysis is valid.

An analogous expression for the y component of the blade force F may be obtained

by applying Newton's Second Law to the control volume. First we observe that the

mass flow rate per unit length of blade is given by rh = pWxt. We then have

(Force applied to (Rate of change of

control volume in = momentum in y

y direction) direction)

or

- Y = rh(Wy2- Wyl)

= pWZt (tan/32 - tan ill)

(2.4)

2.1.1 Case 1 - Frictionless flow

To isolate the effect of the lift force L let us consider first the simpler case of

frictionless fluid flow, for which the stagnation pressure loss Apo will be zero. Making

use of Eqns (2.3) and (2.4) with Apo = 0, the angle % Fig. 2.6, then follows

from

X pW2xttan ~ (tan/31 - tan/32)

tan a = ~ = pW2x t (tan 131 - tan 132) (2.5)

= tan/3oo

or a =/3~. Thus we see from Figs 2.5 and 2.6 that the lift force L is normal to the

vector mean velocity W~, and its components are thus

X= Lsin/3~ I (2.6)

Y= L cos/3~

J

2.1.2 Case 2- Real cascades with fluid friction

For real fluids influenced by viscosity, however, the full X force equation (2.3) must

be used including the loss term Apot. Now this may be attributed entirely to the drag

force D taken in the direction normal to L. Thus making use of both Eqns (2.3) and

(2.4) and resolving forces parallel to D we have

D = Y sin/3~ - X cos/3~

= Apot cos/3o~ (2.7)

Introducing this into the definition of Co, Eqn (2.2b), we obtain

o

CD= 1 2 = 1 2

7cost

~pW~l ~pW~

- cost3

(2.8)

28

Two-dimensional casdades

where the cascade loss coefficient ~'~ based upon vector mean velocity is defined

as

Apo

~oo =1 2 (2.9)

~pWoo

An expression for CL may be derived now as follows. First we obtain the lift force

L from Eqns (2.3) and (2.4):

L = Xsin/3oo + Ycos/3oo

= pW2t(tan/31

- tan/32) sin/3oo - (Apot) sin/3oo

= pW2t

(tan fll

--

tan/32) cos/3oo - (Apo t) sin/3oo

Hence the lift coefficient, Eqn (2.2a), becomes

t ( Apo )(/)

C L --

2 7 (tan

fll --

tan fiE)

COS floo -- 1' 2

sin/300

~pW~

(2.10)

t

= 2 ~- (tan/31 - tan/32) cos/300 - CD tan/3oo

We observe that the presence of viscous drag forces expressed through the drag

coefficient Co results in a reduction of the lift coefficient below that of

CLi

for a

frictionless fluid, namely

t

CLi = 2 ~- (tan/31 - tan/32) cos/300 for frictionless flow (2.10a)

We note also that CL is strongly affected by the term (tan

fll-

tan/32) which itself

is closely related to fluid deflection (/31-/32) as we might expect. CL is also linearly

dependent on the cascade pitch/chord ratio

t/l

as again we would expect,

t/l

and the

'solidity' o-=

l/t

are thus important cascade geometrical parameters through which

the designer can exercise close control over blade loading.

In the case of axial fans, for which the blade spacing is often quite wide, e.g.

t/l ,>

1.0, a rough guide to profile selection is provided by the abundance of published

CL, Co data for isolated aerofoils such as that given by I. H. Abbott and A. E. Von

Doenhoff (1959) or F. Riegels (1961). This reveals that a lift coefficient of value

CL = 1.2 would be close to the maximum achievable for many aerofoils. For a fan

application a more conservative design value of say CL = 0.8 to 1.0 would be desirable

to increase the allowable stall margin. An example will help to illustrate how one

might then select a suitable pitch chord ratio.

Example 2.1

Problem

Given

fll =

65 ~ and 132 = 60 ~ estimate

t/l

for a fan cascade for which CL = 0.8. Given

a CL/CD

ratio of 30 calculate the loss coefficient.

Solution

From Eqn (2.1),

13oo = arc tan ((tan 65 ~ + tan 60~ = 62.71 ~

CD = CL/30 = 0.026 67

From Eqn (2.10),

From Eqn (2.8),

2.2 Diffuser efficiency of a compressor cascade

29

C L d"

C D tan/3oo

2 (tan

fll --

tan J~2)

COS tim

= 2.2519

~ = CD =

0.025 828

(t/l)

cos floo

2.2 Diffuser efficiency of a compressor cascade

While the primary role of a fan is to move large volumes of air or other gas while

raising its pressure sufficiently to overcome the duct system losses, priorities are

reversed for an axial compressor. In view of the requirement for a large pressure

rise, the primary role of the compressor cascade is that of a diffuser. The standard

definition of diffuser efficiency r/D may then be applied:

Actual pressure rise

I"/D-"

Ideal pressure rise

P2 -- Pl

(2 11)

= lo(w?-

Application of the steady flow energy equation for incompressible flow to the control

volume results in

P2- P l = 89 W2 -- W2)-

Apo

so that I'/D may be rewritten

~Po

rid = 1- lp(W 2 _ W~)

and after substitutions from Eqns (2.8) to (2.10)

r/D = 1--

=1-

~Po

pWx 2

tan 13oo (tan

fll --

tan ~2)

sin (2/300) (tan fll

--

tan f12)

(2.12)

or

r/D=l-2(

C~~~i ) 1 (2.13)

sin (2/3~)

As shown by Dixon (1975), quoting Howell (1945), the lift drag ratio

CLi/C D

varies

weakly with/3oo for efficient cascades and may be assumed constant when differentiat-

ing rto to estimate the optimum/300. Thus

dn-----~D~4(CD)COS(2/3~176 =0

for (floo)opt

d/3~ ~Li sin2 (2fl~)

30

Two-dimensional cascades

This simple analysis shows that if we regard a compressor cascade as a diffuser

the optimum performance requires that cos (2/3oo) = 0, that is/3o0 = 45 ~ This provides

a very simple way forward as a basic design guide but of course ignores a wide range

of other factors which may influence compressor performance such as annulus wall

frictional losses, secondary losses due to the impact of the annulus wall boundary

layer upon the blade row, and tip clearance losses due to leakage through the gap

between blade tip and casing. Some of these matters will be dealt with briefly later

where pertinent, but detailed reviews have been given by Dixon (1975) and Horlock

(1958, 1966).

Apart from these additional influences, closer consideration of the blade profile

fluid dynamics reveals how far in practice the actual flow departs from that of an

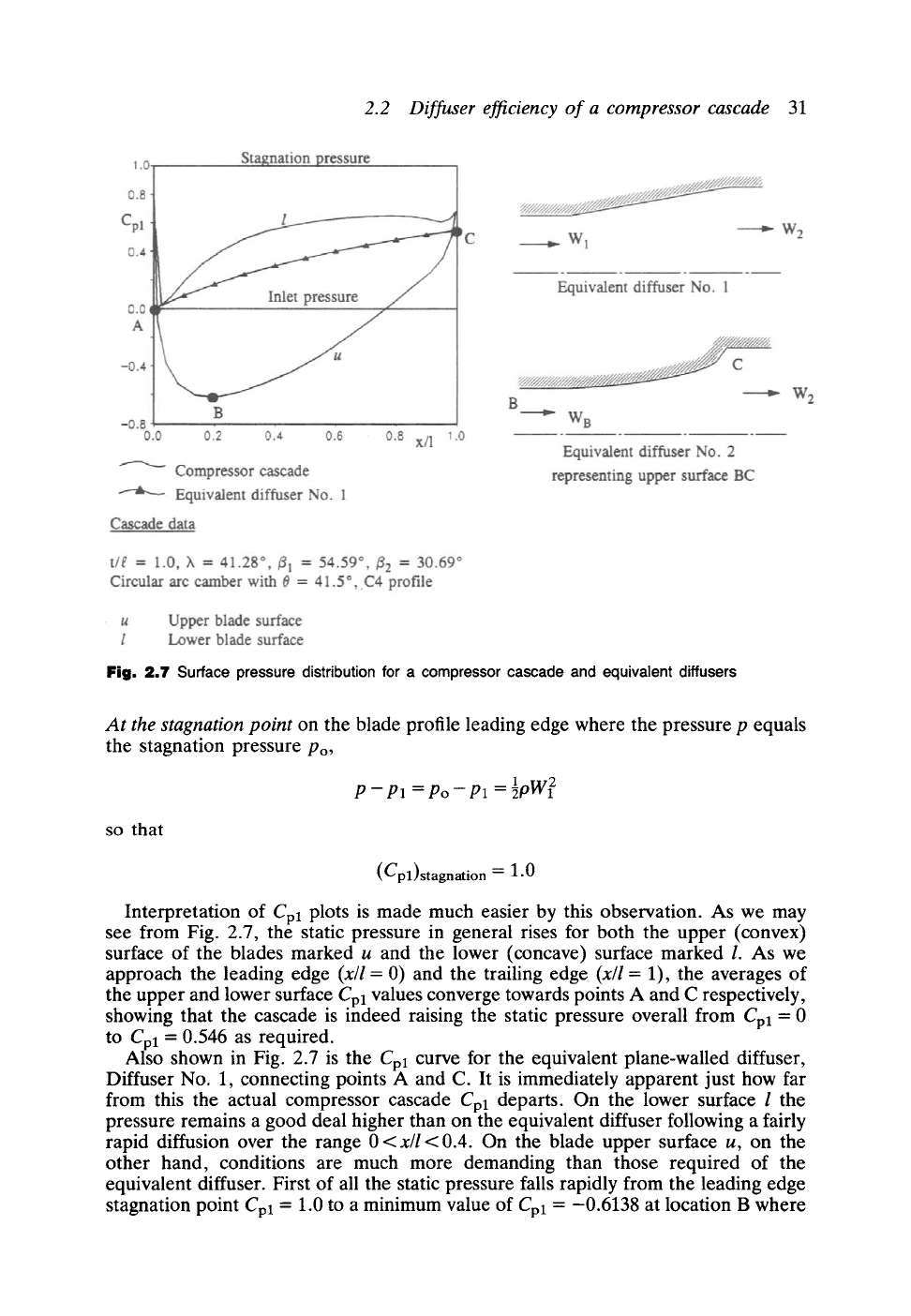
equivalent diffuser. To illustrate this the blade surface pressure distribution fox a

typical well-designed compressor cascade is compared in Fig. 2.7 with the pressure

rise through an equivalent two-dimensional plane walled diffuser, Diffuser No. 1.

For this purpose normal practice in dealing with compressor cascades is to define

a dimensionless surface pressure coefficient Cpl based upon inlet dynamic head:

Cpl --

Pl

-- P12

(2.14)

~pW1

where p is the static pressure on the blade surface and Pl is the static pressure

upstream of the cascade.

The cascade considered here was designed and analysed using the program

CASCADE, in order to deliver an ideal lift coefficient

CLi -'-

1.15, given

t/l

= 1.0 and

/3oo = 45 ~ To achieve this some preliminary analysis is required to determine

fll

and

/32. Equations (2.1) and (2.10a) may be rearranged into the form

tan

fll +

tan

f12 =

2 tan/3oo

CLi

tan fll - tan fiE

=

t (2.15)

2 7 cos/300

providing a pair of simultaneous equations whose solution yields /31 = 54.59 ~

/32 = 30.69 ~ Making use of the design technique outlined in Appendix II, Section

II.8, the cascade was designed for smooth inlet flow to deliver the required outlet

angle and overall fluid deflection

fll- f12--23.90~

Before making general observations about the predicted

Cpl

distribution it is of

help to note the three following special values of the pressure coefficient

Cpl

if we

apply its definition, Eqn (2.14), to conditions upstream and downstream of the

cascade and also to the leading edge stagnation point.

Upstream of the cascade,

point A:

(Cpl)upstream = Pl-Pl

1 2 =0

~PW1

Downstream of the cascade,

point C"

P2--Pl

=1 [W2'~ 2

(Cpl)downstream

= 1 2

~pW1

\Wl]

=1-

(c~ 2

cos/32 = 0.546

2.2 Diffuser efficiency of a compressor cascade

31

Fig.

2.7 Surface pressure distribution for a compressor cascade and equivalent, diffusers

At the stagnation point

on the blade profile leading edge where the pressure p equals

the stagnation pressure Po,

1 2

P - Pl = Po - Pl = gpW1

so that

(Cpl)stagnation = 1.0

Interpretation of

Cpl

plots is made much easier by this observation. As we may

see from Fig. 2.7, the static pressure in general rises for both the upper (convex)

surface of the blades marked u and the lower (concave) surface marked I. As we

approach the leading edge

(x/l

= 0) and the trailing edge

(x/l

= 1), the averages of

the upper and lower surface

Cpl

values converge towards points A and C respectively,

showing that the cascade is indeed raising the static pressure overall from

Cpl --0

to Cpl-0.546 as required.

Also shown in Fig. 2.7 is the

Cpl curve

for the equivalent plane-walled diffuser,

Diffuser No. 1, connecting points A and C. It is immediately apparent just how far

from this the actual compressor cascade

Cpl

departs. On the lower surface l the

pressure remains a good deal higher than on the equivalent diffuser following a fairly

rapid diffusion over the range 0

<x/l

< 0.4. On the blade upper surface u, on the

other hand, conditions are much more demanding than those required of the

equivalent diffuser. First of all the static pressure falls rapidly from the leading edge

stagnation point Cpl = 1.0 to a minimum value of

Cpl =

-0.6138 at location B where

32

Two-dimensional cascades

x/l

= 0.1656. Following this the static pressure has to rise more than double the overall

(P2 -Pl) of the cascade over the remaining upper surface section BC. Thus the upper

or convex surface of a compressor cascade is subjected to extremely high diffusions,

in this example more than double those of the cascade overall equivalent diffuser.

In view of this S. Lieblein (1956) developed an experimental correlation linking this

blade upper surface diffusion between points B and C to cascade losses and loading

limits, since boundary layer growth and stability on this section of a compressor blade

are known to have dominating aerodynamic effects. We will return to this matter

in Section 2.7. For the present purpose it will be instructive just to consider the

equivalent diffuser for the upper surface section BC, shown here as Diffuser No. 2.

The aim is to select its area A as a fraction of the area A1 at inlet with velocity W1

such that the upper surface Cpl value is obtained along the diffuser. If the local

velocity on the blade surface is Vs, then for incompressible flow the continuity

equation gives

A Wl

A1 Vs

But from the definition of

Cpl

p p1=1

Cpl -" 1 2

~pW1

and hence for the equivalent diffuser to model the flow over the blade surface

section BC,

A 1

(2.16)

A--'q- = X/1 - Cpl

From this we observe two things as compared with equivalent diffuser No. 1. First,

much more overall diffusion is required. Second, heavy diffusion demands are made

upon the trailing edge. In practice the thickening boundary layers would tend to

separate close to the trailing edge, contributing to losses and tending also to unload

the blade in that region.

2.3 Specification of blade profile geometry

The foregoing discussion suggests that considerable care is needed when designing

compressors or fans to select profile shapes which will produce stable diffusing flows,

particularly on the vulnerable upper surface. There are two approaches to blade

profile selection which are often referred to as the

direct

(analysis) and

inverse

(synthesis) methods. These may be described briefly as follows"

(1)

Direct (or analysis) method.

Blade profiles are generated by a systematic

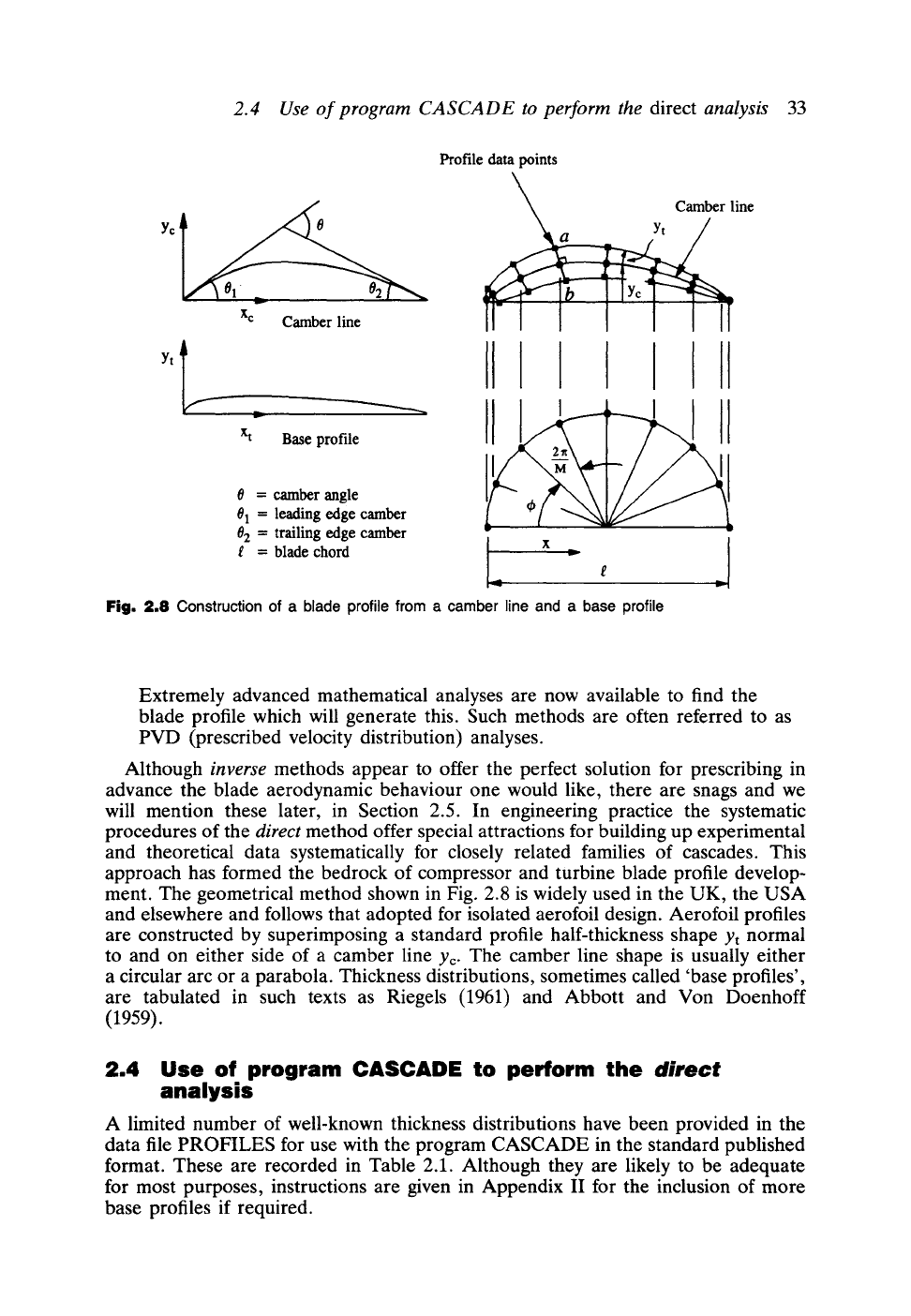
geometrical technique such as that illustrated in Fig. 2.8. Series of such

cascades are then analysed either by experimental test or by theoretical

analysis to identify the most efficient geometries and their detailed

aerodynamic performance.

(2)

Inverse (or synthesis, PVD) methods.

This technique allows the designer to

specify the surface velocity or pressure distribution along the blade surface.

2.4 Use of program CASCADE to perform the direct analysis 33

Yc

v

xc Camber line

v

Base profile

0 = camber angle

01 = leading edge camber

0 2 = trailing edge camber

t = blade chord

Profile data points

Camber line

a

Yt

II

' I

L. e ~

Fig. 2.8 Construction of a blade profile from a camber line and a base profile

Extremely advanced mathematical analyses are now available to find the

blade profile which will generate this. Such methods are often referred to as

PVD (prescribed velocity distribution) analyses.

Although inverse methods appear to offer the perfect solution for prescribing in

advance the blade aerodynamic behaviour one would like, there are snags and we

will mention these later, in Section 2.5. In engineering practice the systematic

procedures of the direct method offer special attractions for building up experimental

and theoretical data systematically for closely related families of cascades. This

approach has formed the bedrock of compressor and turbine blade profile develop-

ment. The geometrical method shown in Fig. 2.8 is widely used in the UK, the USA

and elsewhere and follows that adopted for isolated aerofoil design. Aerofoil profiles

are constructed by superimposing a standard profile half-thickness shape Yt normal

to and on either side of a camber line Yc. The camber line shape is usually either

a circular arc or a parabola. Thickness distributions, sometimes called 'base profiles',

are tabulated in such texts as Riegels (1961) and Abbott and Von Doenhoff

(1959).

2.4 Use of program CASCADE to perform the direct

analysis

A limited number of well-known thickness distributions have been provided in the

data file PROFILES for use with the program CASCADE in the standard published

format. These are recorded in Table 2.1. Although they are likely to be adequate

for most purposes, instructions are given in Appendix II for the inclusion of more

base profiles if required.

Lewis R.I. Turbomachinery Performance Analysis

Подождите немного. Документ загружается.