Lewis R.I. Turbomachinery Performance Analysis

Подождите немного. Документ загружается.

204

Mixed-flow and radial turbomachines

Duty (~e,ffe) for

shock-free inflow

Fig. 7.18 Dimensionless head-flow characteristic for a backward-swept centrifugal rotor

Secondly, we can deduce from the earlier discussion of the physical origin of

relative eddy flows that the magnitude of the slip velocity c02 = W0s is dependent

mainly upon the relative vorticity 2II and the blade passage shal~e, Section 7.5.1 Thus

for a constant speed characteristic ~b =

Cr2/U2

versus qJ =

gh/U~,

since f~ is constant

the dimensionless slip factor

coJU2

can be determined from any convenient duty

(~b, q0. The obvious choice of duty to make is the 'shut-off' head ho for which the

flow coefficient is zero, ~bo = 0. From Eqn (7.49) we then have

COs

= 1 - tro (7.50)

where tro is the slip factor for zero mass flow. Introducing this into Eqn (7.48), the

slip factor for any other flow rate ~b becomes

tro- ~b tan/3[

tr = 1 - ~b tan/3~ (7.51)

The dimensionless characteristic (th, q0 curve for the impeller is illustrated in Fig. 7.18,

in which point O is the shut-off head duty ~b = 0, qJ = qJo. Its equation follows from

the Euler pump equation since

gh Co2

_ , ch (

(for zero prewhirl machines)

1 - Wb2u2 ) = or(1 - ~b tan/3~) (7.52)

Introducing Eqn (7.51)into this, we have finally the alternative expression for the

constant speed characteristic curve in terms of the shut-off head slip factor tro:

qJ = tro - 4~ tan/3[ (7.53)

1We will return to this assumption later at the end of Section 7.5.3.

1.0

0.8

0.6

0.4-

0.2

0.0

1.0

'Z=16 ' ' ' ] 1.0 [ ' Z-16 ' ' ' ]

2, 0.6

0.4

0.2

0.0

0.2.1 0.4 0.6, 0.8 1.0 0.0 012 014 016 0.8 1.0

r~/r2 rl/r2

Z=16

I i I

0.8

fro

0.6

0.4

0.2

0.0

7.5 Relative eddy and slip flow in radial and mixed-flow turbomachines

205

fl = 80 ~

0.2 0.4 0.6 0.8 1.0

rl/r2

Z = number of

blades

Vane angle fl js measured from radial direction

Fig.

7.19 Predicted shut-off head slip factors Oo for swept-back centrifugal impellers, after Busemann

(1928)

Thus the theoretical frictionless characteristic (losses have been ignored here) is linear

and is determined by the vane angle/3~ and the shut-off head coefficient qJo, which,

from Eqn (7.53), is given by qJo = tro.

The maximum flow which can be delivered at point M on the characteristic, Fig.

7.18, is thus for the condition q, = 0, namely

~bM = fro/tan/3~ (7.54)

Busemann (1928), in his comprehensive foundation paper on this subject, gave

shut-off head slip factors for a wide range of vane angles for centrifugal impellers

with logarithmic-spiralled blades (i.e. with constant vane angle/3 =/3~ from leading

edge to trailing edge). Figure 7.16(b) shows Busemann's results for the special case

/3 = 0 ~ for radial blades. A selection of his predicted data for vane angles in the useful

range for swept-back rotors is shown in Fig. 7.19 for/3 = 10 ~ 20 ~ and 40 ~ Busemann's

classical model as given was restricted to infinitely thin log-spiral blades. It is possible

to extend his method to a family of blades with finite profile thickness and camber

as shown by Fisher and Lewis (1972) for the case of radial blades, but these are of

206

Mixed-flow and radial turbomachines

1.0

0.8

0.6

0.4

0.2

/J= 50 ~

0.0

0.0 0.2

i !

0.4 0.6 0.8 1.0

rl/r2

1.0

0.8

~0.6

0.4

0.2

0.0

0.0 0.2 0.4 0.6 0.8 1.0

rl/r2

1.0

0.8

~tO. 6

0.4

0.2

0.0

i i i

1) -

2 4 \

0.2 0.4 0.6 0.8

r/r2

Z = number of blades

Vane angle/3

is measured from radial direction

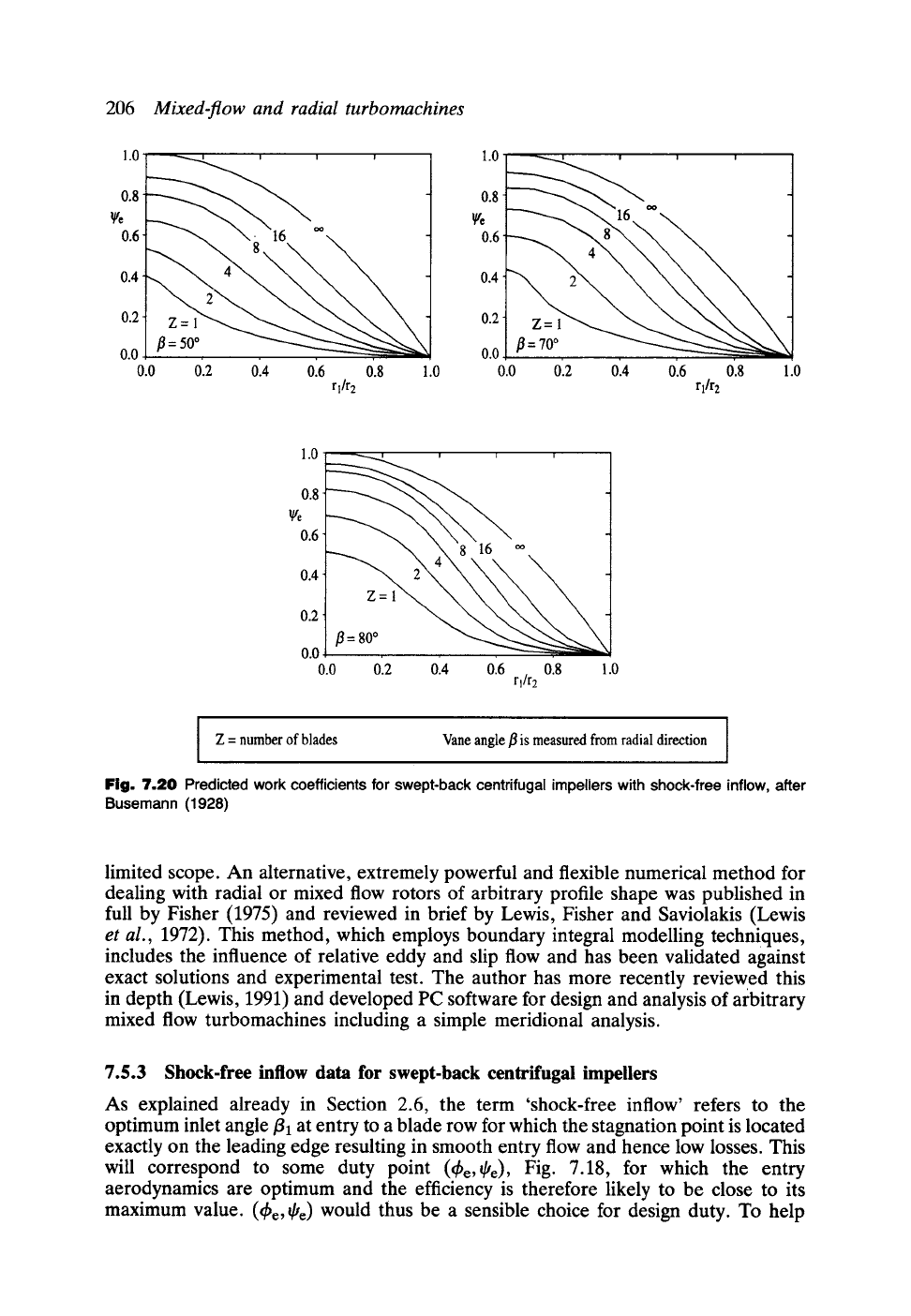
Fig. 7.20 Predicted work coefficients for swept-back centrifugal impellers with shock-free inflow, after

Busemann (1928)

limited scope. An alternative, extremely powerful and flexible numerical method for

dealing with radial or mixed flow rotors of arbitrary profile shape was published in

full by Fisher (1975) and reviewed in brief by Lewis, Fisher and Saviolakis (Lewis

et al.,

1972). This method, which employs boundary integral modelling techniques,

includes the influence of relative eddy and slip flow and has been validated against

exact solutions and experimental test. The author has more recently reviewed this

in depth (Lewis, 1991) and developed PC software for design and analysis of arbitrary

mixed flow turbomachines including a simple meridional analysis.

7.5.3 Shock-free inflow data for swept-back centrifugal impellers

As explained already in Section 2.6, the term 'shock-flee inflow' refers to the

optimum inlet angle

fll

at entry to a blade row for which the stagnation point is located

exactly on the leading edge resulting in smooth entry flow and hence low losses. This

will correspond to some duty point (~be, qJe), Fig. 7.18, for which the entry

aerodynamics are optimum and the efficiency is therefore likely to be close to its

maximum value. (~be, qJe) would thus be a sensible choice for design duty. To help

7.5 Relative eddy and slip flow in radial and mixed-flow turbomachines 207

with design duty selection Busemann used his theoretical analysis to produce the

curves shown in Fig. 7.20.

For a given vane angle /3, number of blades Z and radius ratio rl/r2, the work

coefficient for shock free inflow qJe has a unique value available from these curves.

The corresponding flow coefficient

t~e

then follows from the characteristic curve, Eqn

7.53, namely

t~e---- (O" o -- q~e)/tan/3~ (7.55)

As already stated, Busemann's data, both Figs 7.19 and 7.20, are applicable only

to rotors with thin backward-swept log-spiral blades and with zero prewhirl, col = O.

Numerical methods such as the author's MIXEQU computer code are able to

lift these restrictions totally and provide accurate (although only frictionless)

design/analysis facilities for the whole range of radial or mixed-flow fans or turbines,

usually with incompressible flow. An example will help to illustrate the use of the

above analysis.

Example 7.3

Problem

A centrifugal pump has eight log-spiral blades with vane angle/3 = 70 ~ and radius

ratio rl/r2 = 0.6. Use the above data and analysis to estimate the following:

(1) The shut-off work coefficient qJo.

(2) The maximum flow coefficient ~bM.

(3) The shock-free duty (the, q~e).

For shock-free flow calculate the relative inlet and outlet angles,/31 and/32, and the

slip factor try.

Solution

(1) From Fig. 7.19, %

(2) From Eqn (7.54),

= 0.85.

~bM = go/tan/3~ = 0.85/tan 70 ~ = 0.309 37

(3) From Fig. 7.20, q~e

curve),

= 0.33, and thus from Eqn (7.53) (the characteristic

~e = (~ - q~e)/tan/3~ = 0.1893

Calculation of

fll

tan

fll -"

Hence

fll --

62.26~

Calculation of

f12

rl ~~ --- r2 ~'~ X cr2

X~-- rl -~~(rl) 2

Crl Cr2 Crl r2 r2

tan

f12 ---

w02 U2- c02 U2- ~'U2 1 -

Cr2 Cr2 Cr2 r

Hence

f12 --

74.22~

208 Mixed-flow and radial turbomachines

Note that the relative eddy increases/32 but decreases /31 as compared with the

vane angle/3 for the case of shock-free inflow.

From Eqn (7.51) the slip factor for shock-free inflow is

0.85 - 0.1893 tan 70 ~

= 0.6874

~ = 1 - 0o 1893 tan 70 ~

Reconsideration of the assumption regarding Cos

In Section 7.5.2 a crucial assumption was made regarding the slip velocity Cos that

led to simplifications, namely that the slip velocity 'is dependent mainly upon the

relative vorticity 2~ and the blade passage shape'. Now co is vectorially equal to

w2- w~, Fig. 7.17. Thus the slip velocity represents the departure of the actual exit

velocity relative to the rotor from the actual blade exit angle. Clearly this is influenced

by the relative eddy 2f~ but also by any variation of the inflow angle/31 at different

flow coefficients. As was shown in Chapter 2 for straight cascades, the outlet angle

/32 will depend upon the inlet angle/31 (in this case with no relative eddy for the

straight cascade), but significantly so only if the pitch/chord ratio is greater than unity.

Applying this to centrifugal machines, the foregoing analysis and use of Busemann's

data is therefore valid provided t/l < 1. From Eqn (7.35) this is satisfied for log-spiral

blades if

27r cos/3

Zln(r2/rl)

< 1.0 (7.56)

In most practical designs t/l will be less than unity and the above procedures are then

justified. The full Busemann analysis does not in fact require this assumption but

is rather more complex and difficult to apply.

7.6

Some other slip factor formulations for radial and

mixed-flow fans and pumps

One of the earliest slip factor formulations was proposed by Stodola (1927) based

upon the assumption which was qualified in the last paragraph. Referring to Fig. 7.21,

Stodola assumes that the slip velocity cOs is approximately equal to the circulation

velocity around the throat circle C of diameter d due to the relative eddy. Thus

Circulation ~ (vorticity inside circle)x area

d 2

C os ,rd ~ 2I~ ,r ~

The diameter d may also be approximated by

27rr2

d~ t2 cos/3~ Z

cos/3~

where t2 is the circumferential pitch at radius r2. Combining these equations we have

finally

COs -=

"/rr 2 ~'~ COS ~

7.6 Some other slip factor formulations for radial and mixed-flow fans and pumps

209

2nr2 /

Fig. 7.21 Throat section of swept-back impeller

and from Eqn (7.48) the slip factor approximates to

tr = 1 - (,r/Z)

cos/3~ (Stodola) (7.57)

1 - 4) tan/3~

Stanitz (1952) undertook a remarkably thorough and penetrating theoretical study

of centrifugal and mixed-flow compressors by finite difference modelling, concentrat-

ing mainly on radially bladed machines but including some studies with modest

sweep-back angles/3 of 26.56 ~ and 45 ~ . In addition to slip factors his analysis delivered

detailed streamline predictions, such as that shown already in Fig. 7.16(a), for various

flow coefficients and also blade surface velocity distributions indicating the presence

of a standing eddy with reversed flow at low 4, values and the special influence of

compressibility. According to his findings the slip velocity Cos was dependent upon

blade number Z only, and the earlier expression of Stanitz and Ellis (1950) was

justified irrespective of vane angle/3, namely

Cos = 0.63r21~Tr/Z

so that the slip factor, Eqn (7.48), can then be expressed as

0.637r/Z

or = 1- (Stanitz) (7.58)

1 - 4,2 tan/3~

Although compressibility was found to influence his predicted streamline patterns

within the blade passage, Stanitz found its influence upon slip factor to be negligible

for the cases considered.

7.6.1 Slip factors for mixed-flow fans and pumps

Lewis (1966) derived exact conformal transformation solutions for mixed-flow

turbomachines with straight blades of zero stagger. This analysis was later extended

by Fisher and Lewis (1972) to profiled symmetrical or cambered blades. Although

there is a lack of data on slip factors for mixed-flow machines, these analyses have

established that a correct estimate of tr for a mixed-flow fan or pump with cone angle

210

Mixed-flow and radial turbomachines

3', Fig. 7.13, is given by that for an equivalent radial machine with M blades

where

M = (7.59)

sin 3'

This follows directly from the conformal transformation theory outlined in Section

7.4.1, although in this case transforming the mixed-flow cascade into an equivalent

radial (rather than straight) cascade. The analysis of Stanitz (1952) confirms this

approach. Thus all of the foregoing formulations may be applied directly to

mixed-flow pumps and fans.

Ducted

propellers

and fans

Introduction

The main function required of the various turbomachines considered so far is the

rotodynamic transfer of energy between an impeller and the fluid passing through

a carefully prescribed constraining annulus such as that of the mixed-flow fan

illustrated in Fig. 8.1(a). In the case of a pump or fan the requirement is to'move

a given volume flow rate of fluid while at the same time increasing its stagnation

pressure or enthalpy, these two tasks being typified by the related duty coefficients

(th, ~) as defined by Eqns:(4.2) and (4.4).

The ship or aircraft propeller is no less a rotodynamic pumping device by means

of which shaft input work may be converted into energy increase of the through-flow

fluid. As illustrated by Fig. 8.1(b), however, the operational requirements of a

propeller are usually quite different from those of an axial or mixed-flow fan, even

though the blade shapes and the aerodynamic/rotodynamic mechanisms are very

similar. Firstly propellers operate in 'open water' so that the energised fluid is finally

delivered at ambient pressure p~. Secondly the main purpose of a propeller is usually

the production of thrust for the purpose of propulsion. This is achieved in reaction

to the momentum developed by the jet exit velocity Vj as a result of the energy

transferred to the fluid. The basic principles underlying this will be elaborated in

Section 8.1 including a suitable definition of propulsive efficiency.

The ducted propeller or fan illustrated in Fig. 8.2(a) sits half-way between these

two extremes. Firstly, such devices are required to operate in the 'open water'

situation and to deliver thrust in reaction to a fluid jet Vj delivered finally at ambient

pressure. On the other hand the propeller is now located within a duct of short length.

Although the duct in a sense fulfils the role of the turbomachine annulus casing in

guiding the fluid through the blade space, its primary duty is much more important

Poo ~p=

_ / _~

(a) (b)

Fig. 8.1 Turbomachine and propeller configurations: (a) mixed-flow fan; (b) open propeller

212

Ducted propellers and fans

By-pass

fan

Gas

(a) (b)

Fig. 8.2 Ducted propeller and by-pass fan configurations: (a) ducted propeller or fan; (b) by-pass

engine

and complex than this. For ducted propulsors the total forward thrust T is shared

between the propeller Tp and the duct Td. Typically in a highly loaded unit the duct

may actually supply as much as 30% of the total thrust. The benefit of this feature

is twofold, namely (a) an increase in the total possible achievable thrust for a given

propeller diameter and (b) an increase in propulsive efficiency. The basic principles

underlying this will be explained in Section 8.2. A design and performance analysis

will be developed in Sections 8.3 and 8.4 including a discussion of the main fluid

dynamic loss mechanisms and related analysis. A simple method for prediction of

the off-design performance characteristics will be developed in Section 8.5.

8.1 One-dimensional actuator disc performance analysis

for open propellers

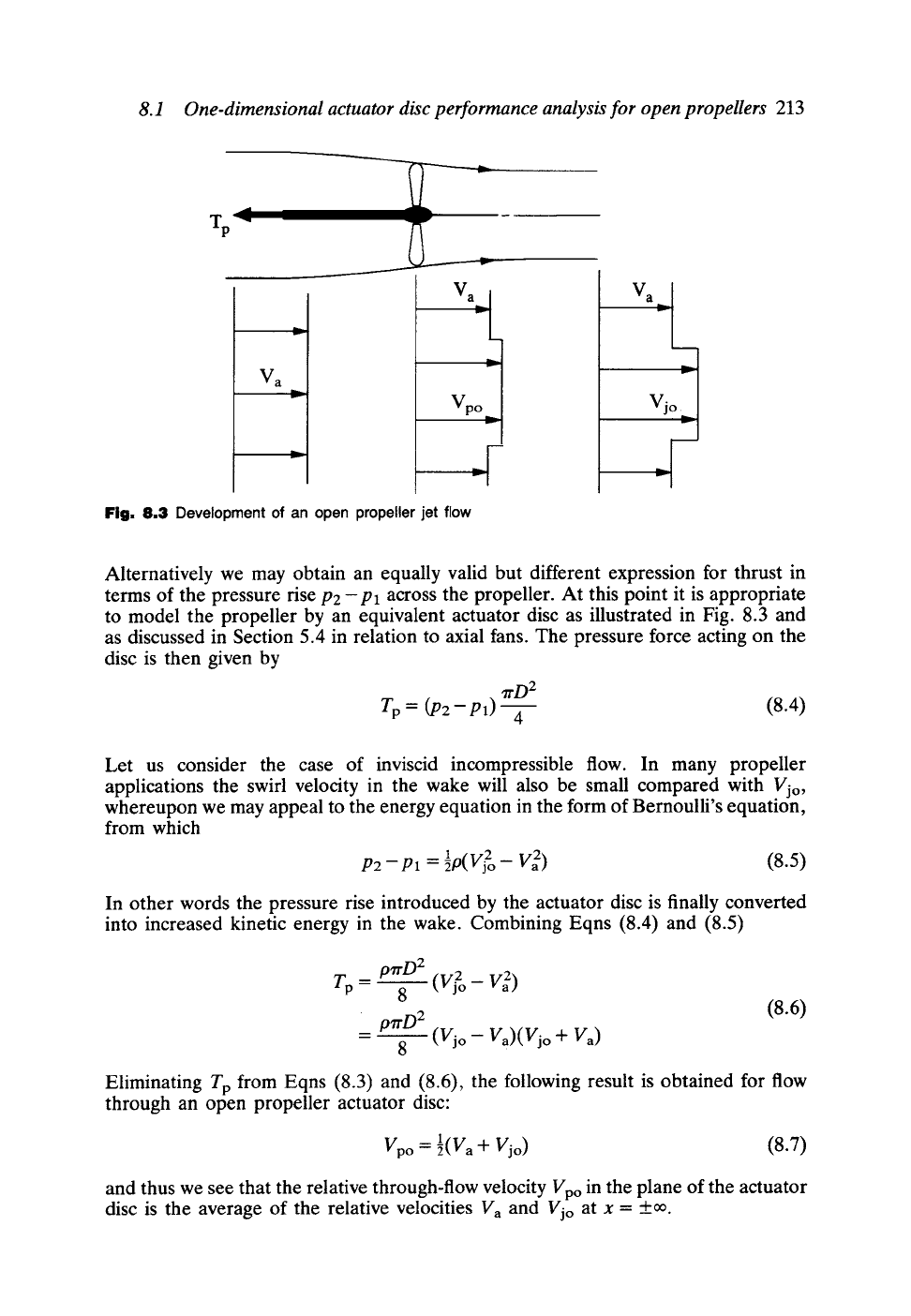
Figure 8.3 depicts the flow viewed relative to a propeller and illustrates the slipstream

contraction associated with the progressive rise of the through-flow velocity from Va

a long way upstream to Vjo in the downstream jet. For simplicity we shall assume

here that the specific work input and consequent stagnation enthalpy (compressible

fluids) or stagnation pressure (incompressible fluids) is the same for all streamlines

passing through the area swept out by the propeller and that the through-flow velocity

rises to Vpo in the plane of the propeller. Applying Newton's second law, the propeller

thrust is then given by

Tp = rh(Vjo - Va) (8.1)

where the mass flow rate rh through the propeller is given by

~rD 2

rh = p---~- Vpo (8.2)

and where for simplicity we are neglecting the area occupied by the propeller hub.

Thus

~rD 2

Tp = p ~ Vpo(Vjo- Va) (8.3)

8.1 One-dimensional actuator disc performance analysis for open propellers

213

Va.~ I

Vpo

.j-

Fig. 8.3 Development of an open propeller jet flow

._J

"-1

Alternatively we may obtain an equally valid but different expression for thrust in

terms of the pressure rise P2- Pl across the propeller. At this point it is appropriate

to model the propeller by an equivalent actuator disc as illustrated in Fig. 8.3 and

as discussed in Section 5.4 in relation to axial fans. The pressure force acting on the

disc is then given by

7rD 2

Tp = (Pz-pl) 4 (8.4)

Let us consider the case of inviscid incompressible flow. In many propeller

applications the swirl velocity in the wake will also be small compared with Vjo,

whereupon we may appeal to the energy equation in the form of Bernoulli's equation,

from which

1 2

p~ -pl = ~p(Vjo - V2a)

(8.5)

In other words the pressure rise introduced by the actuator disc is finally converted

into increased kinetic energy in the wake. Combining Eqns (8.4) and (8.5)

P wD2 (V2o- V2a)

Tp= 8

p,n.D 2

(Vjo- Va)(Vjo + Va)

(8.6)

Eliminating Tp from Eqns (8.3) and (8.6), the following result is obtained for flow

through an open propeller actuator disc:

gpo -- I(V a -k- gjo ) (8.7)

and thus we see that the relative through-flow velocity Vpo in the plane of the actuator

disc is the average of the relative velocities Va and Vjo at x = +~.