Lewis R.I. Turbomachinery Performance Analysis

174 Vorticity production in turbomachines and its influence upon meridional flows

Applying this equation at the hub radius r h"

T1-

T2h = ~

(6.84a)

2Cp

Dividing the last two equations results finally in

:1 (1

rl rl

]

(6.85/

Now the exit temperature at the hub T2h can be expressed in terms of the given Mach

number M2h. Thus

C2h C2h

m2h = ~ =

a2h

V'TRT2h

where a2h is the local speed of sound, or

C2h Uh2(~ + ~b2h)

T2h =

yRM2h = (3,_ 1)cpM2h

(6.86)

where tha

=

dPm(r/rh)

and g'h

=

~m(r/rh) 2.

Combining Eqns (6.84a) and (6.86) we then

have finally

TEh 1

TI

1+ Y--IM2h (2 4}2+ $2h ) $2 h

(6.87)

The density ratio across the stator blade row at any radius is thus now fully specified

in terms of the given data

rh/rt,

~m, ~m,

M2h

and ~Tr through Eqns (6.83), (6.85)

and (6.87).

6.6.4 Compressible meridional flow through a turbine stage

The previous analysis may be extended with little difficulty to model a complete

turbine stage by the introduction of a second actuator disc to represent the rotor.

Assuming that there is no swirl at entry to and at exit from the stage and that Cx3

~-

Cxl ,

the overall enthalpy drop may be expressed as

~U 2 = hol - h03 ~ hi - h3 = Cp(T1 - T3)

If

h01- h03

is to be equal at all radii,

T3= T3h= Tl-~

Cp

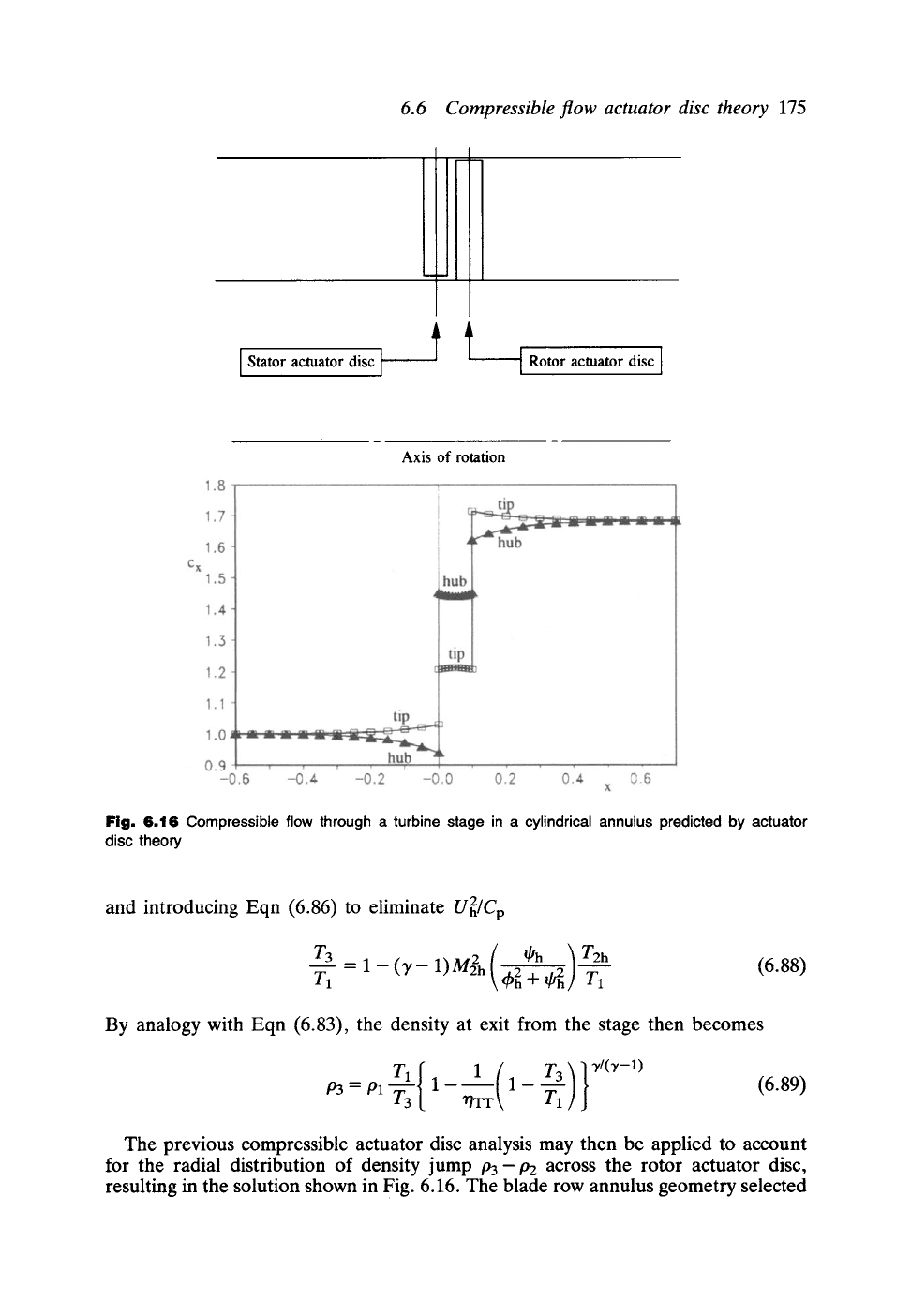
I Stator actuator disc[

6.6

Compressible flow actuator disc theory

175

Rotor actuator disc I

Axis of rotation

Fig. 6.16 Compressible flow through a turbine stage in a cylindrical annulus predicted by actuator

disc theory

and introducing Eqn (6.86) to eliminate

U2/Cp

73

T1

~h ) T2h

=l--(3,--1)M~h 4)2+~h

T1

(6.88)

By analogy with Eqn (6.83), the density at exit from the stage then becomes

p3=Pl 1- 1--~- 1

r/TT

(6.89)

The previous compressible actuator disc analysis may then be applied to account

for the radial distribution of density jump P3- P2 across the rotor actuator disc,

resulting in the solution shown in Fig. 6.16. The blade row annulus geometry selected

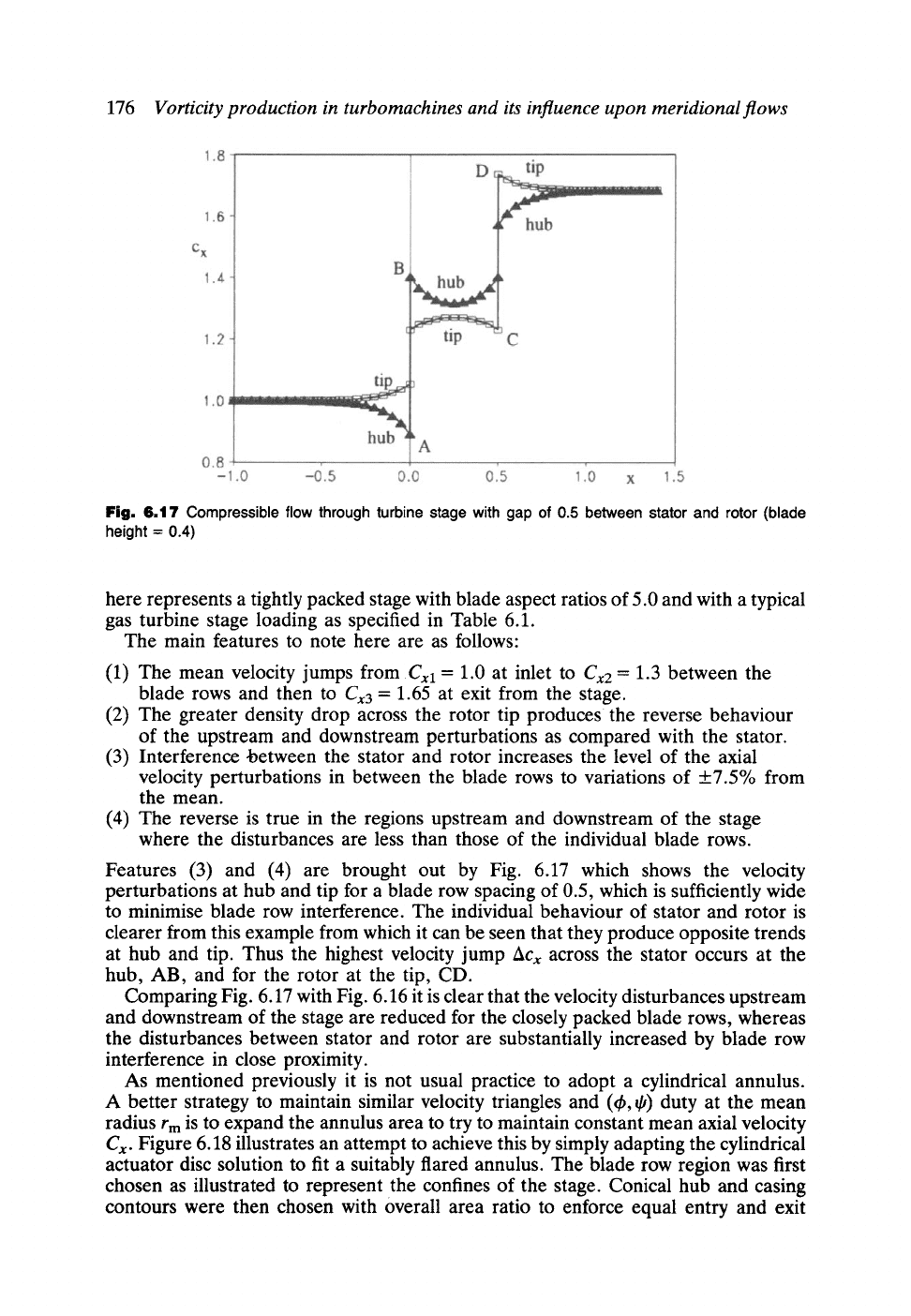
176

Vorticity production in turbomachines and its influence upon meridional flows

Fig. 6.17 Compressible flow through turbine stage with gap of 0.5 between stator and rotor (blade

height = 0.4)

here represents a tightly packed stage with blade aspect ratios of 5.0 and with a typical

gas turbine stage loading as specified in Table 6.1.

The main features to note here are as follows:

(1) The mean velocity jumps

from Cxl =

1.0 at inlet to

Cx2

= 1.3 between the

blade rows and then to

Cx3

= 1.65 at exit from the stage.

(2) The greater density drop across the rotor tip produces ~ the reverse behaviour

of the upstream and downstream perturbations as compared with the stator.

(3) Interference between the stator and rotor increases the level of the axial

velocity perturbations in between the blade rows to variations of +7.5% from

the mean.

(4) The reverse is true in the regions upstream and downstream of the stage

where the disturbances are less than those of the individual blade rows.

Features (3) and (4) are brought out by Fig. 6.17 which shows the velocity

perturbations at hub and tip for a blade row spacing of 0.5, which is sufficiently wide

to minimise blade row interference. The individual behaviour of stator and rotor is

clearer from this example from which it can be seen that they produce opposite trends

at hub and tip. Thus the highest velocity jump

Acx

across the stator occurs at the

hub, AB, and for the rotor at the tip, CD.

Comparing Fig. 6.17 with Fig. 6.16 it is clear that the velocity disturbances upstream

and downstream of the stage are reduced for the closely packed blade rows, whereas

the disturbances between stator and rotor are substantially increased by blade row

interference in close proximity.

As mentioned previously it is not usual practice to adopt a cylindrical annulus.

A better strategy to maintain similar velocity triangles and (~b, qJ) duty at the mean

radius r m

is to

expand the annulus area to try to maintain constant mean axial velocity

Cx.

Figure 6.18 illustrates an attempt to achieve this by simply adapting the cylindrical

actuator disc solution to fit a suitably flared annulus. The blade row region was first

chosen as illustrated to represent the confines of the stage. Conical hub and casing

contours were then chosen with Overall area ratio to enforce equal entry and exit

6.6 Compressible flow actuator disc theory

177

r m

A

l

Axis of rotation

rh

I Stator

x

Rotor actuator disc I

actuator disc [

1.4

C x

1.0

9 A A ,L A

0.6

-0.6 -o.

4

,i

tip

'

tip

9 ~.. -= A A - -~ 9 " " A A ,= k

-0.2 0.0 ' 0J. x 0:6

I Blade row region [

Fig. 6.18 Compressible flow

through annulus with area

increase to

maintain constant mean axial

velocity

mean axial velocities

Cx

= 1.0. For all other x locations the

Cx

values shown in Fig.

6.17 were simply scaled to satisfy mass flow continuity. While this cannot be justified

rigorously from a fluid-dynamic point of view, it does at least offer a simple design

approach leading to a first-order assessment of meridional disturbances due to

compressibility. From Fig. 6.18 one can conclude that these disturbances will in

general be small outside the confines of the stage. Within the stage, however, where

the density gradient 'action' is taking place, there will be much more significant

variations in

Cx

which need the attention of a more advanced analysis. The plane

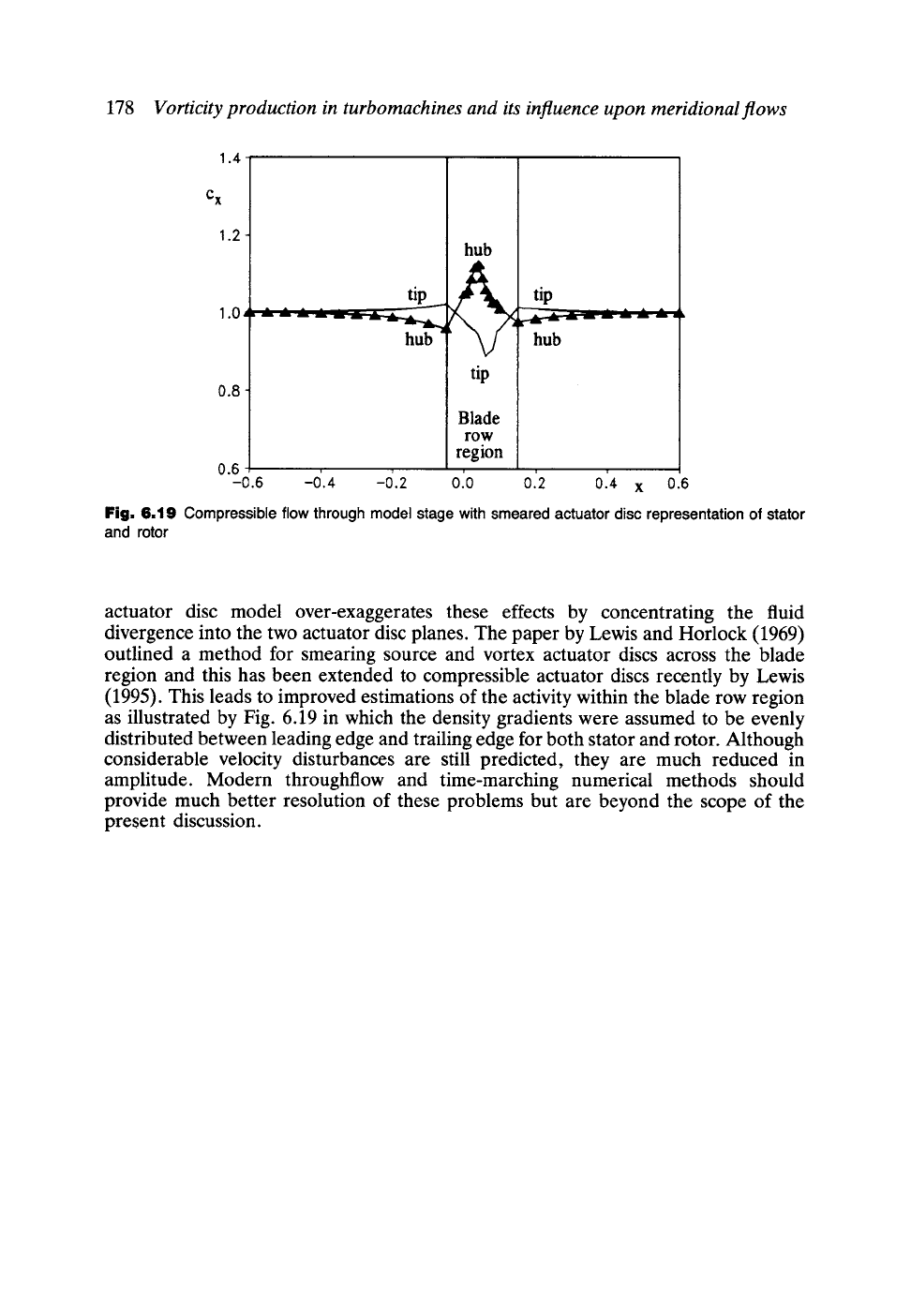
178

Vorticity production in turbomachines and its influence upon meridional flows

1.4

c x

1.2

1.0

0.8

A . A .

hub

tip

hub

Blade

row

region

0.6

-o.6 -o'.4 -o'.2

olo

x 0.6

Fig. 6.19 Compressible flow through model stage with smeared actuator disc representation of stator

and rotor

actuator disc model over-exaggerates these effects by concentrating the fluid

divergence into the two actuator disc planes. The paper by Lewis and Horlock (1969)

outlined a method for smearing source and vortex actuator discs across the blade

region and this has been extended to compressible actuator discs recently by Lewis

(1995). This leads to improved estimations of the activity within the blade row region

as illustrated by Fig. 6.19 in which the density gradients were assumed to be evenly

distributed between leading edge and trailing edge for both stator and rotor. Although

considerable velocity disturbances are still predicted, they are much reduced in

amplitude. Modern throughflow and time-marching numerical methods should

provide much better resolution of these problems but are beyond the scope of the

present discussion.

7

Mixed-flow and

turbomachines

radial

Introduction

In the early days of the development of the aircraft gas turbine engine there was fair

competition between the multi-stage axial compressor and the centrifugal compressor

as contenders for the same task, namely the delivery of large volume flow rates of

air to the engine with fairly high pressure ratios. Competition was fair in the sense

that these quite different devices have their own particular advantages and

disadvantages. As illustrated by Fig. 7.1(a) and the data shown in Figs 1.11 and 1.13

and the related discussion in Section 1.2.2 of Chapter 1, several stages of an axial

compressor would be required to deliver the same pressure ratio as that which can

be produced by a single stage centrifugal compressor.

On the other hand, for the same inlet area and meridional inlet velocity

Csl,

the

centrifugal compressor presents two inconvenient geometrical features. Firstly the exit

diameter must be much greater than the inlet diameter to obtain the centrifugal effect

and consequent high head rise. Secondly the flow path is turned radially outwards,

delivering the air unhelpfully in the radial direction and requiring an exit volute. The

axial compressor, on the other hand, while presenting the expense of its many blade

rows, is geometrically ideally suited to the general throughflow requirements of a

modern aircraft gas turbine engine which will comprise an axial turbine and an axial

bypass fan in addition to the multi-stage axial compressor.

For more general applications fans fall into the three categories illustrated in Fig.

7.1(b), namely axial, mixed-flow and radial (or centrifugal). These configurations and

their general characteristics have been very helpfully reviewed by ESDU (1980) to

assist the non-specialist with fan selection and with tender appraisal, including the

presentation of Fig. 1.13. Regions for optimum efficiency of each category of fan are

plotted first against axes of specific diameter Ds versus specific speed Ns and secondly

against axes of 9 versus 9 where these coefficients are defined as in Eqns (1.16)

and (1.23), namely

O

ND 3

gH

xtt = N2 D 2

[1.16]

(I) 1/2

N s = xir

xi1'1/4

Ds-- (i)1/2

Specific speed

Specific diameter

[1.231

180

Mixed-flow and radial turbomachines

Csl

(a)

rE.

(b)

Fig. 7.1 Meridional

flow through (a) axial and centrifugal compressors and (b) axial, mixed-flow and

radial

fans

The spread of 'practice' recorded in Fig. 1.13(a) is generally quite close to the

well-known curve of Cordier (1953) and marks out axial fans as suited to

high specific

speeds

while centrifugals are the appropriate choice for

low specific speeds.

To

summarise, the selection ranges suggested by Fig. 1.13(a) are given in Table 7.1.

Table

7.1 Recommended selection ranges for axial, mixed-flow and radial fans

Specific speed Ns range

Fan type

0.5 to 2.0 Radial

2.1 to 3.2 Mixed-flow

1.4 to 13.0 Axial

These data suggest quite wide ranges of Ns appropriate for axial and centrifugal

or radial fans even with a measure for possible overlap in the middle range,

1.4 <Ns <2.0. Alternatively in this range it may be just as appropriate to select

instead a mixed-flow fan, so named because its configuration is a mixture of both

the axial and the radial machines, Fig. 7.1(b). Such fans have fulfilled a crucial role

in high technology applications such as gas-cooled nuclear reactor circulators and

hovercraft lift fans for which a combination is required of high mass flow rate and

fairly high pressure ratio (i.e. more than that capable of a single stage axial) at high

efficiency. The range of applications suggested by Table 7.1 and Fig. 1.13 is, however,

unnecessarily restricted and simply reflects the limits set by 'practice'. It would be

perfectly possible for mixed-flow fans to serve a much wider range of specific speeds

than the above data suggest, offering perhaps the advantages of fewer stages than

an axial fan or the more suitable throughflow annulus shape as compared with a

radial fan.

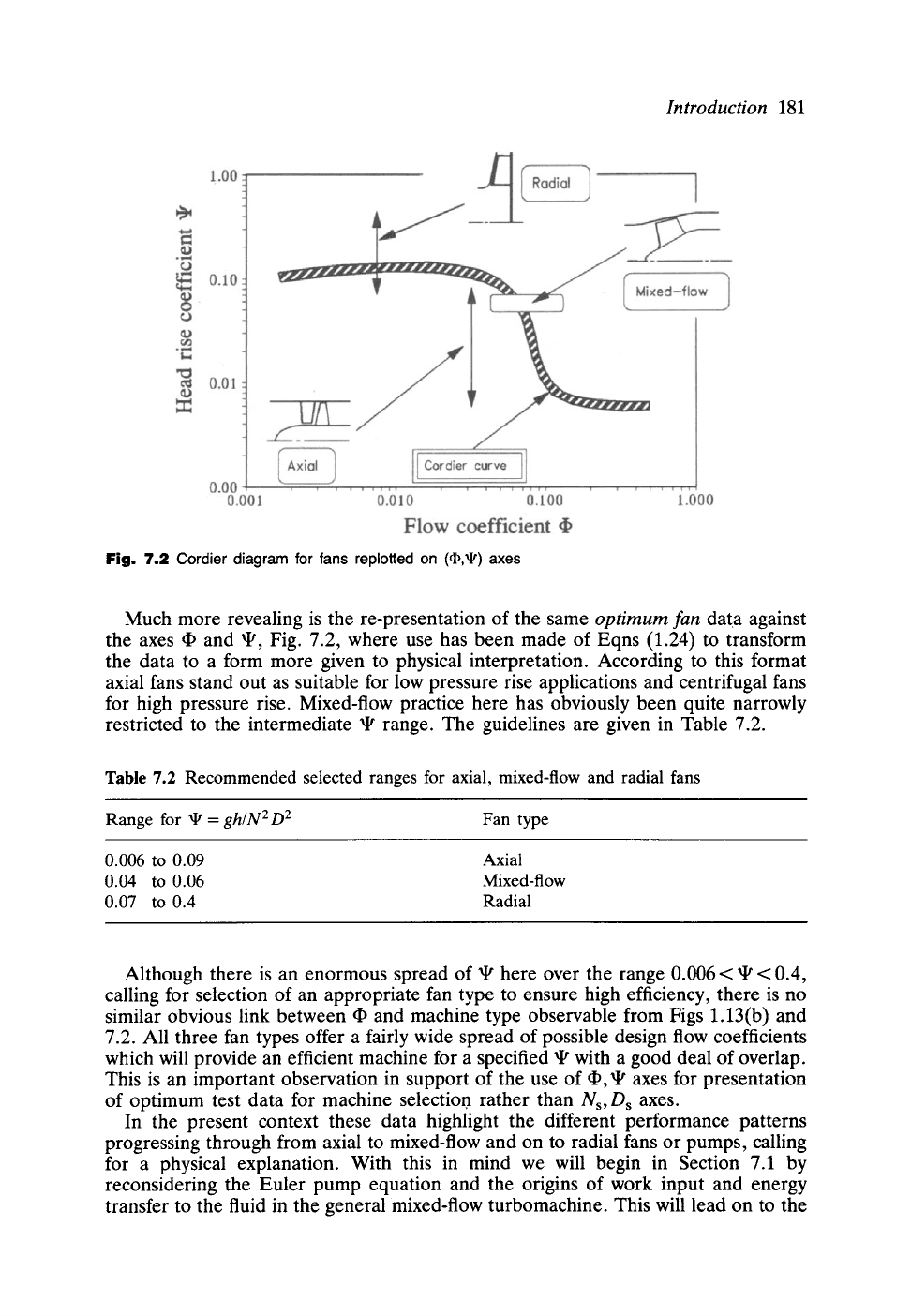
Introduction 181

Fig. 7.2

Cordier diagram for fans replotted

on

((]),~) axes

Much more revealing is the re-presentation of the same

optimum fan

data against

the axes 9 and ~, Fig. 7.2, where use has been made of Eqns (1.24) to transform

the data to a form more given to physical interpretation. According to this format

axial fans stand out as suitable for low pressure rise applications and centrifugal fans

for high pressure rise. Mixed-flow practice here has obviously been quite narrowly

restricted to the intermediate 9 range. The guidelines are given in Table 7.2.

Table 7.2 Recommended selected ranges for axial, mixed-flow and radial fans

Range for 9 =

gh/N2D 2

Fan type

0.006 to 0.09 Axial

0.04 to 0.06 Mixed-flow

0.07 to 0.4 Radial

Although there is an enormous spread of 9 here over the range 0.006 < ~ < 0.4,

calling for selection of an appropriate fan type to ensure high efficiency, there is no

similar obvious link between 9 and machine type observable from Figs 1.13(b) and

7.2. All three fan types offer a fairly wide spread of possible design flow coefficients

which will provide an efficient machine for a specified 9 with a good deal of overlap.

This is an important observation in support of the use of ~, 9 axes for presentation

of optimum test data for machine selection rather than

N~,Ds

axes.

In the present context these data highlight the different performance patterns

progressing through from axial to mixed-flow and on to radial fans or pumps, calling

for a physical explanation. With this in mind we will begin in Section 7.1 by

reconsidering the Euler pump equation and the origins of work input and energy

transfer to the fluid in the general mixed-flow turbomachine. This will lead on to the

182 Mixed-flow and radial turbomachines

derivation of the property rothalpy relevant to energy transfer in rotating systems

with radial flow, Section 7.2. Dimensionless velocity triangles will then be considered

in Section 7.3 to link stage duty based on local dimensionless variables (~b, q0, machine

overall radius ratio (r2/rl) and annulus area ratio (A2/A1) with expressions for stage

efficiency to link with the performance philosophy developed in Chapters 3 and 4

for axial turbines and compressors.

The handling of the general three-dimensional design problem of a mixed-flow

turbomachine by the combination of an axisymmetric meridional flow and a series

of mixed-flow cascades will be introduced in Section 7.4. To conclude the chapter,

Section 7.5 will be given to the problems of the relative eddy and the related slip

which occur in radial and mixed-flow pumps and fans and appropriate correlations

for their estimation.

7.1

Origins of specific work input in mixed-flow fans and

pumps

The potential ability of radial and mixed-flow fans and pumps to deliver higher head

rise coefficients than axial machines is revealed if the Euler pump equation is

re-expressed relative to the rotor. As shown in Chapter 1, Eqn (1.9a) and Fig. 1.5,

the Euler pump equation for a mixed-flow fan may be expressed as

m

W = ho2-hol =

U2c02 - U1r

(7.1)

where if" is the specific work input (J kg-1), U = rI~ is the local blade speed and

co is the absolute swirl velocity. Now co is related to the swirl velocity wo measured

relative to the rotor at any point at radius r within the rotor, through

co = U + wo = rf~ + wo

(7.2)

where Co and Wo are defined as positive in the direction of the rotor blade velocity

U. Introduction of this into Eqn (7.1) results in the following alternative and revealing

form of the Euler pump equation:

1~ = ho2- hol

= U 2 w02- U 1 wol + U 2 - U?

= I~(r2 WOE- rl wol) + I~2(r2- rE) (7.3)

wor in ut) wor )

-- due to aerodynamic -t- due to Coriolis

forces forces

For axial machines, since r = constant, this reduces to

m

W = f~rl(wo2-

Wol)

(7.3a)

In this special case all the specific work input derives from the blade aerodynamic

forces set up in reaction to the fluid deflection e

= fll- f12, Fig.

7.3. For the case

of the mixed-flow fan, on the other hand, we are able to identify two separate

sources

of work input as stated by Eqn (7.3). These are as follows:

(1) Specific work input due to aerodynamic forces results from the change in

angular momentum of the flow viewed relative to the rotor, IrE WOE- rlWoll.

(2) A second specific work contribution completely independent of blade profile

7.1 Origins of specific work input in mixed-flow fans and pumps 183

Fig. 7.3 Velocity triangles for an axial fan

Fig. 7.4 Coriolis acceleration and force on a particle of mass m in a rotating slider

shape and therefore of aerodynamics and entirely dependent upon meridional

streamline radial shift

between inlet rl and exit r2, Fig. 7.4, namely

fl2(r 2 -r2). This can be identified as originating from the Coriolis forces

exerted on the fluid by the rotor by virtue of their radial component of

velocity

Cr. To confirm this let us consider the simpler but analogous

situation of a solid particle of mass m being propelled radially outwards with

velocity ~ =

dr/dt in a rotating radial slider, Fig. 7.4. The Coriolis acceleration

Lewis R.I. Turbomachinery Performance Analysis

Подождите немного. Документ загружается.