Lewis R.I. Turbomachinery Performance Analysis

144

Vorticity production in turbomachines and its influence upon meridional flows

The principal aims of this chapter are

(a) to develop the meridional equations for axial and mixed-flow

turbomachines, and

(b) to show the underlying vortex production mechanisms linking two types of

vorticity generated by turbomachinery blade rows, namely

streamwise vorticity

and

smoke-ring vorticity.

These matters will be dealt with in Sections 6.1 to 6.4, including a full derivation

of the equations of motion for axisymmetric flow and the reduction of these to form

a set of governing equations for turbomachinery meridional flows. The origin of the

classical actuator disc solution for cylindrical annuli as already used in Chapter 5 will

then be presented briefly in Section 6.5. To conclude this chapter, solutions will be

developed for compressible flow through actuator discs, Section 6.5, including recent

extensions of this to include annulus area changes needed to accommodate density

decrease in multi-stage axial turbines.

r~

(

[

'

pC r + OpCr

dr

Or

pc x ~1~

dr

PCx+

dx

Per

OPCx

dx

Ox

v

x

OPCo OPCr

dr

PC o

+ dO

O0 PCr+ Or

/-

pc

o

/ ~

MJ

(a) (b)

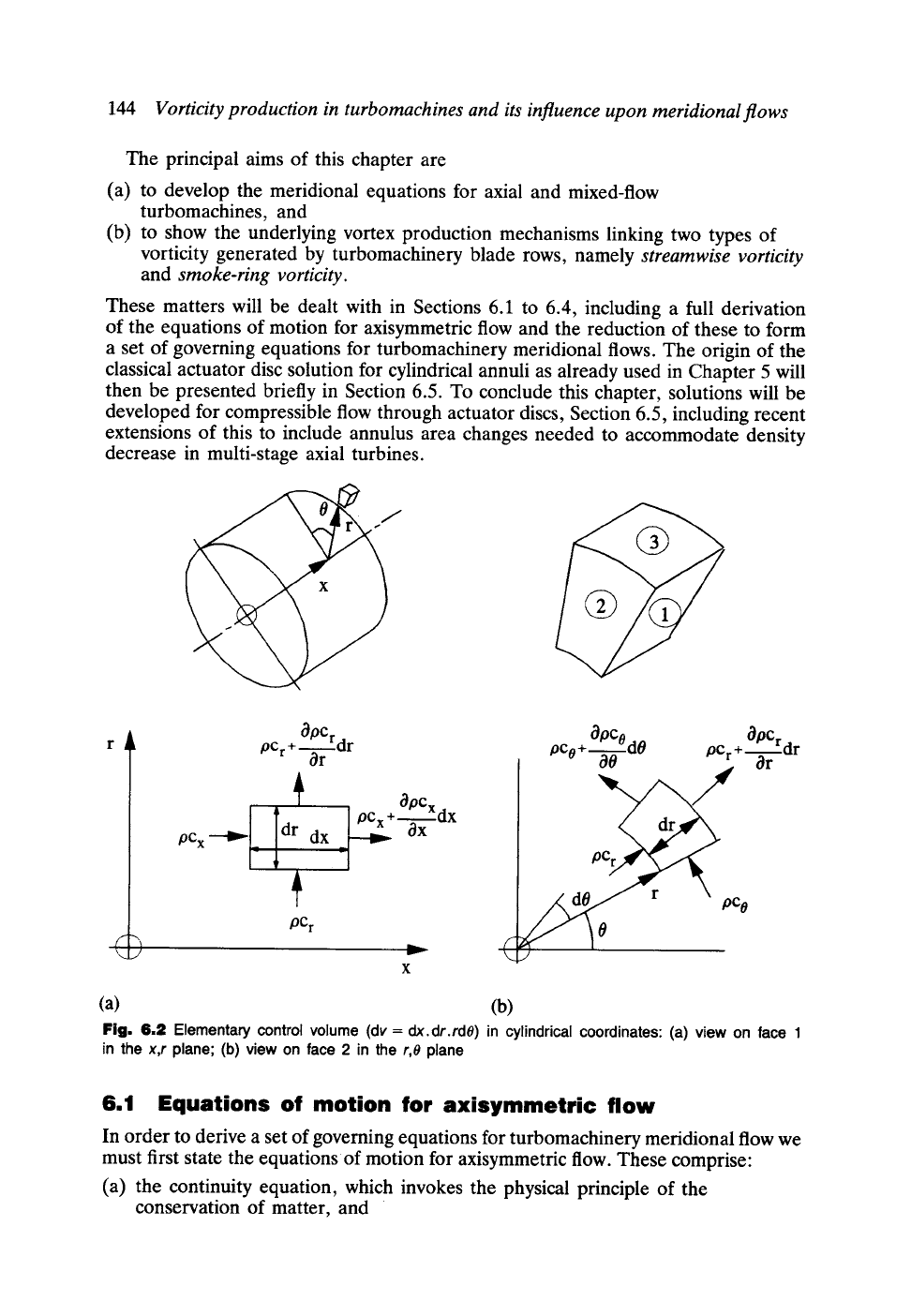
Fig. 6.2 Elementary control volume (dv =

dx.dr.rdO)

in cylindrical coordinates: (a) view on face 1

in the

x,r

plane; (b) view on face 2 in the

r,O

plane

6.1 Equations of motion for axisymmetric flow

In order to derive a set of governing equations for turbomachinery meridional flow we

must first state the equations of motion for axisymmetric flow. These comprise"

(a) the continuity equation, which invokes the physical principle of the

conservation of matter, and

6.1 Equations of motion for axisymmetric flow 145

(b) the momentum equations, which invoke Newton's second law as applied to a

fluid.

These will be dealt with in turn in the following subsections, adopting cylindrical polar

coordinates, (x,r, 0), Fig. 6.2.

6.1.1 The continuity equation

Applying the principle of conservation of matter to the elementary control volume

dV = dx.dr.rdO, Fig. 6.2, the net mass flux leaving the control volume must be

equated to zero. For axisymmetric flow all derivatives in the 0 direction such as

a(pc0)/ao must be zero. Accounting for the mass flux through opposite pairs of faces

of the element we thus obtain

rgOC.

(faces 2) {pc x + -~.-x dx - pCx} r d0 dr

Ox

0/:1C r

(faces 3)

{pC r +

dr) (r + dr)dO dx

-

PCrr

dO dx = 0

Or

(6.1)

Neglecting terms of second order of smallness, this equation reduces to the continuity

equation for axisymmetric steady compressible flow"

OPCx ogpCr [~7 r

+ + = 0 compressible flow (6.2)

ax Or r

For incompressible flow the density p is constant, resulting in the simpler form

r r C r

OCx~ +--=0

ax 0r r

incompressible flow

(6.3)

Alternatively the continuity equation may be expressed in vector form through

div Pq = 0 compressible flow ]

(6.4)

div t~ = 0 incompressible flow

Several important analytical derivations pertinent to meridional flows can be made

from the continuity equation and we will return to this matter again in Sections 6.3

and 6.6. At this point, on the other hand, it will be more helpful to introduce the

momentum equations.

6.1.2 The momentum equations for axisymmetric flow in Eulerian form

If Newton's second law is applied to the elementary control volume, Fig. 6.3, then

for any specified direction

Applied forces on )

the control volume

Rate of change of momentum of)

the fluid crossing the boundary

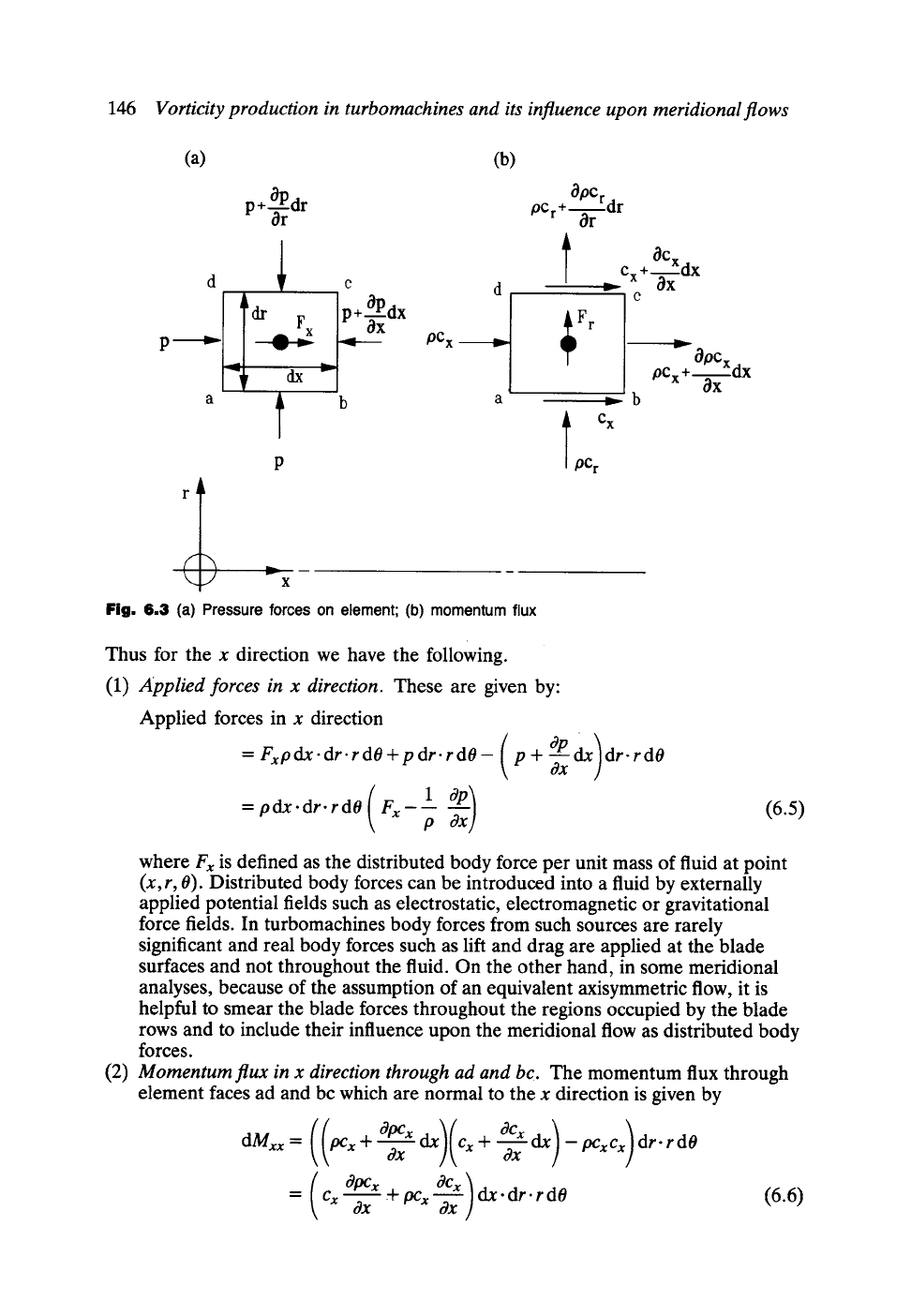
146

Vorticity production in turbomachines and its influence upon meridional flows

(a) (b)

p+

igPdr

Or

/

d ~ c d

lldr Fx P+ ~-~Px dx

p ---'-'~ ~ ~ PCx

pC r +

cgPCr

dr

Or

t

~

F r

aC x

c x +--~- dx

dx

a t b a l ~b c x

P PCr

m

Fig. 6.3 (a) Pressure forces on element; (b) momentum flux

v

pc x + OPCxdx

#x

Thus for the x direction we have the following.

(1)

Applied forces in x direction.

These are given by:

Applied forces in x direction

=Fxpdx'dr'rdO+pdr'rdO-(p+OPdx)

(a x)

= pdx.dr.rdO Fx P

(6.5)

where

Fx

is defined as the distributed body force per unit mass of fluid at point

(x,r, 0).

Distributed body forces can be introduced into a fluid by externally

applied potential fields such as electrostatic, electromagnetic or gravitational

force fields. In turbomachines body forces from such sources are rarely

significant and real body forces such as lift and drag are applied at the blade

surfaces and not throughout the fluid. On the other hand, in some meridional

analyses, because of the assumption of an equivalent axisymmetric flow, it is

helpful to smear the blade forces throughout the regions occupied by the blade

rows and to include their influence upon the meridional flow as distributed body

forces.

(2)

Momentum flux in x direction through ad and bc.

The momentum flux through

element faces ad and bc which are normal to the x direction is given by

) )

Ox -~-x dX - pCx Cx dr . r d O

( Ocx

OpCx + PCx dx. dr. r dO

= Cx ox ox ]

(6.6)

6.1 Equations of motion for axisymmetric flow 147

where the term involving the product

(OpCx[OX)(OCx]Ox)dx 2

has

been

neglected, being of second order of smallness.

(3) Momentum flux in x direction through ab and cd. It is perhaps less obvious

that fluid is convected through the element sides ab and cd even though they

are parallel to the x direction, due to the radial velocity component Cr. Such

momentum flux can be expressed through

- -4 t- r dO dx dr (6.7)

-

Cr Or p Or

r

where once again second-order terms have been neglected. Combining Eqns

(6.5a) to (6.7) the momentum equation in the x direction becomes

=~[

OpCr Per t OCx OC x

_lap apCx + + + Cx-- x + c,

Fx p Ox Ox Or r Or

But from the continuity equation (6.2) the term in braces {} is zero.

Applying the same derivation procedure in the r and 0 directions the full set of

momentum equations for axisymmetric flow may be obtained, namely

G

m Dm

G

~ Dm

1 3p Oc~ Oc~

-- + C r

pOX - Cx OX O r

10p OCr OCr

: -b C r

p Or Cx Ox Or

OCo OCo

f ~ = Cx--~x

-4- Cr

Or

4

r

COCr

.4=.

r

(6.8)

Together with the continuity equation (6.2) or (6.3), these form the equations of

motion or Eulerian equations for axisymmetric inviscid (frictionless) fluid flow.

6.1.3

Alternative form of momentum equations in terms of stagnation pressure

and vorticity

The momentum equations may be expressed in terms of the stagnation pressure Po

if we introduce the definition

Po = P + c2 c2 c2

p p T+T+T

Thus, differentiating these partially with respect to x and r, for incompressible flow

we have the expressions

10p

_ 1 @o OCx

OCr OCo

pax - - V;x - - V;x

1@ 1@o

p Or p 3r

~~ ~ C X

0C x 0C r OC O

- Cr - C O

148 Vorticity production in turbomachines and its influence upon meridional flows

so that Eqns (6.8) transform to

Fx mmm

Fr m n~

1@o (~Cxt~Cr)

t~r 0

p OX -- Cr Or OX

-c~

= (OCxOCr) cOorcO

1 apo -Cx

par Or Ox r Or

0co Cr Orco

Fo = cx

-I- --~

ax r Or

(6.9)

At this point it is helpful to introduce vorticity which in vectors is defined as

tb = curl~. Expressed in cylindrical polar coordinates the three components of

vorticity, Lamb (1945), become

1 acor 1

aC r

tOx -- -

r Or r 00

1 aCx aCo

tO r ~. _

r O0 Ox

ac r oc x

t~176 ax Or

(6.10)

For axisymmetric flows, since 0/00 = O, these reduce to

1 Ocor

r ar

~0

3x

~r acx

3x 3r

(6.11)

and we see immediately that the momentum equations (6.9) simplify to

1 apo

p Ox

1 apo

p Or

~ _.Fx = c rtO O- C O to r

--~- Fr= cotOx-CxtOO

-- F 0 -- CxtO r - CrO) x

In vector notation this may be stated as

1

--gradpo-P= ~ x tb = ~ x V x

p

(6.12)

(6.13)

In this form the momentum equations tell us that the presence of stagnation pressure

gradients or distributed body forces within a fluid in motion are associated with

distributed vorticity tb with vector direction normal to the local velocity ~. In

axisymmetric flow since apoDO = 0 then the grad Po vector lies in the (x, r) meridional

6.2 Comparison of the radial equilibrium equation

149

plane. Thus the tangential vorticity component too, which is normal to the meridional

velocity Cs, Fig. 6.1, will play the major role in controlling the meridional flow.

Turbomachinery blade rows are designed to control and manipulate the swirl

velocity

co

in order deliberately to produce changes of stagnation pressure Po or

enthalpy ho in exchange for shaft work. Thus blade rows are in essence the producers

of vorticity and later in Section 6.3 we will return to this important subject of vorticity

production in turbomachines which is the key mechanism at the heart of meridional

flow analysis. Before proceeding with this it will be helpful to reconsider briefly the

radial equilibrium analysis of Chapter 5 in the light of the radial equation of motion.

6.2

Comparison of the radial equilibrium equation with the

true radial momentum equation

The radial momentum equation (6.9b), in the absence of body forces, may be

rewritten

1 @o

OCx co arco

t~C r

p ar =Cx 8r -~ Cx

r Or Ox

Now as shown in Chapter 5 the radial equilibrium equation (5.14) is given by

1 dpo

dcx co drco

p dr =CXdr -t

r dr

Radial velocity components

Cr

are assumed to be zero in radial equilibrium analysis

and we see that these equations are identical apart from the last term,

Cx(OCr/OX).

Let us pause briefly to examine this assumption of radial equilibrium theory by

reference to Fig. 6.4 which illustrates the behaviour of

Cr

and thus

OcflOx

in the

neighbourhood of a single blade row. The meridional streamline radial shifts required

to accommodate the build-up of the axial velocity profile

Cx

to its radial equilibrium

value

Cxo~

imply a growth and decay of

Cr

symmetrically about x = 0 as illustrated.

Taking the differential of this curve, Fig. 6.4(b), we see that

C~Cr/OX ~

0

as x--~ +oo

as expected for radial equilibrium at a long distance from the blade row. It is of

interest to note that surprisingly

OCr/OX

will also vanish at x = 0, for example in the

plane of an equivalent actuator disc (see Section 5.4). Curiously, in this plane the

equation of motion momentarily reduces to the radial equilibrium equation even

though

Cr

itself is non-zero. More important, however, are the regions A and B just

upstream and downstream of the blade row where maximum meridional disturbances

occur, of special importance should they interfere with neighbouring blade rows.

Actuator disc theory as outlined in Chapter 5 provides a very good estimate of these

meridional disturbances and associated mutual blade row interference for multi-stage

cylindrical turbomachines. Here we observe that they are due to radial redistributions

of mass flow caused by radial velocities

Cr.

These effects are vortical in nature and

caused by the tangential vorticity too produced by the blade row, which provides the

fluid dynamic link between velocity components

Cx

and

Cr

through its definition, Eqn

(6.10c), namely

0) 0 =

acr ac~

ax ~r

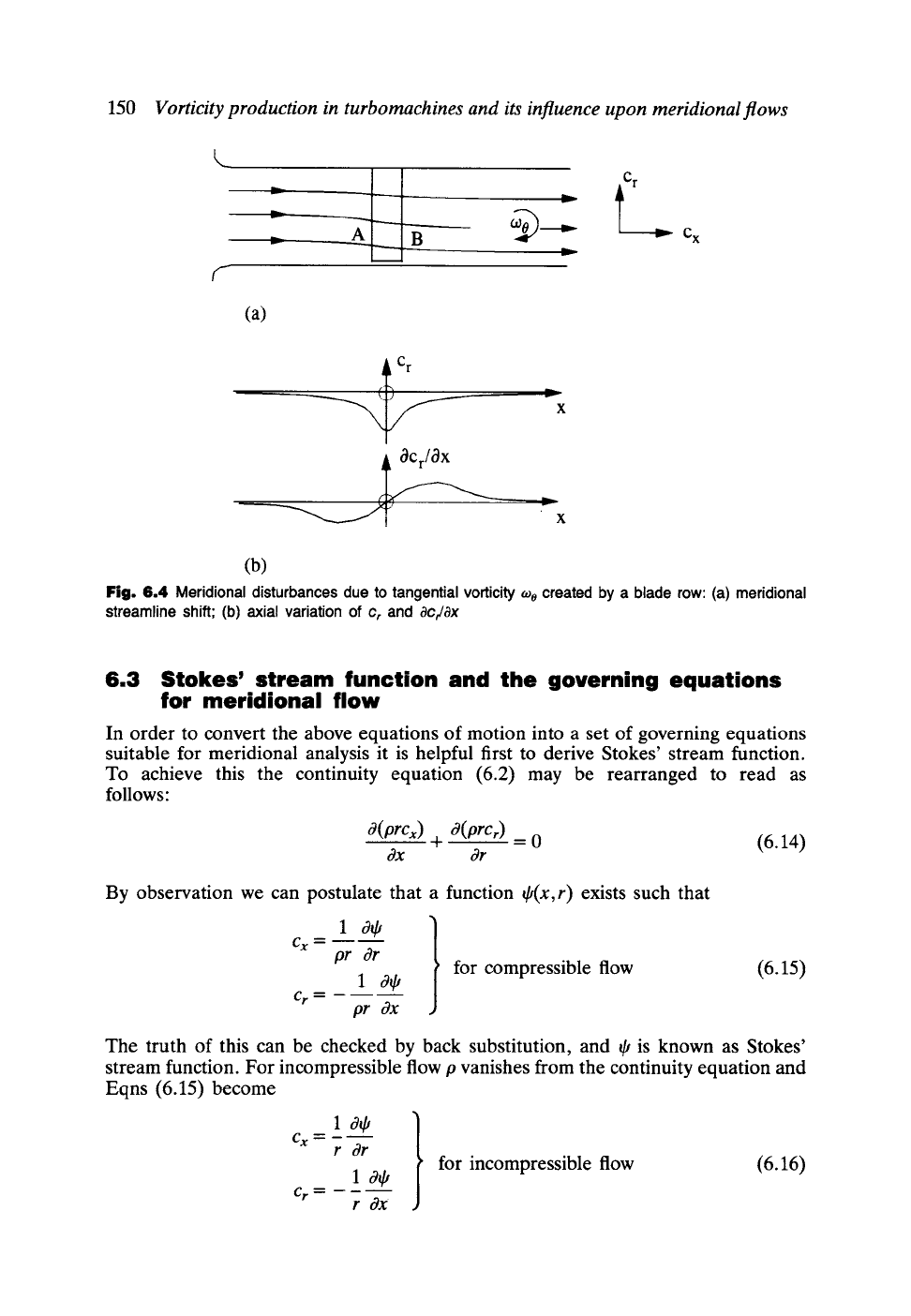
150

Vorticity production in turbomachines and its influence upon meridional flows

(a)

9---

C x

x

c r

(b)

Fig. 6.4 Meridional disturbances due to tangential vorticity

to o

created by a blade row: (a) meridional

streamline shift; (b) axial variation of

Cr

and

aCr/aX

6,3

Stokes' stream function and the governing equations

for meridional flow

In order to convert the above equations of motion into a set of governing equations

suitable for meridional analysis it is helpful first to derive Stokes' stream function.

To achieve this the continuity equation (6.2) may be rearranged to read as

follows"

tg(prcx) a(prcr)

~+~=0 (6.14)

ax Or

By observation we can postulate that a function ~(x,r) exists such that

1 aqJ

Cx = or Or

10q, for compressible flow

Cr=

p r Ox

(6.15)

The truth of this can be checked by back substitution, and ~, is known as Stokes'

stream function. For incompressible flow p vanishes from the continuity equation and

Eqns (6.15) become

_1 ar

Cx r Or

1 ar

C r ~--

r Ox

for incompressible flow

(6.16)

6.3 Stokes' stream function and the governing equations for meridional flow

151

6.3.1 Properties of the stream function - incompressible flow

Stokes' stream function has the characteristics of a potential whose derivative in a

given direction multiplied by

1/r

gives the velocity component at right-angles

clockwise. Its other more significant property is that contours qJ = constant define

the meridional streamlines. To confirm this, since qJ is a function of both x and r

its derivative is given by

d~ = dx + dr

Ox Or

(6.17)

= r(-c r dx + c x

dr)

where use has been made of Eqn (6.16).

Now the slope a of a meridional streamline, Fig. 6.5, is given by

c r dr

tan a = ~ =

Cx dx

or -

Cr dx + Cx dr = 0

Introducing this into Eqn (6.17) we see that along a meridional streamline

or

dqJ=0 }

qJ = constant

(6.18)

(6.19)

Introducing Eqn (6.18) back into (6.17) the following useful result is obtained:

O~ O~ = 0 (6.20a)

Cx--~x + Cr Or

In vector notation this becomes

q" grad q~ = 0 (6.20b)

v

Cx

C r

Fig. 6.6 Slope of a meridional streamline r

152

Vorticity production in turbomachines and its influence upon meridional flows

In other words the gradient (derivative) of q, in the direction of the local meridional

velocity ~ is zero. That is, qJ is constant along the meridional streamlines and hence

its title

stream function.

6.3.2 Governing equation in Stokes' stream function - incompressible flow

If we now eliminate

Cx

and

C r

from the third vorticity component too, Eqn .(6.10c),

by introducing Eqns (6.16), then

CgC r

t~C x = -~X r -~r

tO o = _ _

ax ar ax ~ r

and finally we have Stokes' equation for incompressible rotational axisymmetric

flow"

~q, laq, ~q,

O~X 2 r

Or t- --O--~ - = - tO ~ r

(6.21)

This is now our principal governing equation for incompressible meridional flow and

its solution q, yields the meridional streamline distribution for an annular space

containing a specified spatial distribution of tangential vorticity too. Although the

numerical solution of this equation seems straightforward enough, subject to annulus

wall boundary conditions q, = ~h and q,

= ~t

along hub and casing respectively, one

big problem remains, namely the spatial distribution of too. This requires the

derivation of an auxiliary equation linking too to the swirl velocity

Co

and the

stagnation pressure Po. Further analysis to accomplish this will be undertaken in the

next two subsections.

6.3.3

flows

In the absence of body forces the momentum equations (6.12) become

1 apo

= Crto O- CotO r

pax

1 apo

= Cotox - Cxtoo

p ar

0 = Cxtor- Crtox

Convection of stagnation pressure and angular momentum in axisymmetric

(6.22)

If the first two are combined to eliminate too we obtain

0

Cx- x

O

@ Cr -~t "= PCO(Crtox- Cxtor)

and introducing the third equation we have finally

or

apo apo =0

Cx-~x "k" Cr ar

~-grad Po = 0

(6.23)

6.3 Stokes' stream function and the governing equations for meridional flow 153

Comparing this result with Eqn (6.20) we see that Po, like the stream function q,,

remains constant along the meridional streamlines. Thus, as might be expected, the

stagnation pressure Po is conserved along the meridional streamlines. Now the third

momentum equation (6.22), introducing the vorticity definitions for tax and

tar

from

Eqns (6.11), may be expressed in similar format, namely

or

Orco Orco

+C r

=0

Cx Ox Or

q" grad (rco) = 0

(6.24)

Thus we see that angular momentum rco is also proven to be conserved along the

meridional streamlines. These conservation laws may be summarised as follows"

cor

= f1($) l (6.25)

Po ='f2(6)

J

and the quantities Po and cor are unique functions of $.

6.3.4 Auxiliary equation for too

We may now bring together all of these analytical/physical results to obtain an

auxiliary equation linking Po and cor to the tangential vorticity too. Thus since

Po = f2(q'), Eqn (6.25), while $ = f(x,r) (Section 6.3), the total derivative of Po with

respect to $ may be expressed as

1 dpo 1 @o dx 1 0/90 dr

=

p dq~ p Ox dq~ p Or dqJ

Introducing Eqns (6.22a) and (6.22b), this becomes

p

dO

= ~Oo Cr -~ -- C x + Co tax -'~ -- tar

(6.26)

However, from Eqn (6.17) the first bracketed expression on the right-hand side

reduces to -1/r. The second bracketed expression on the right-hand side may also

be simplified if we use Eqn (6.25a) to obtain the total derivative of cor with respect

to ~,, namely

dcor Ocor dx Ocor dr

de ax dO ar de

and from the definitions of vorticity, Eqns (6.11a) and (6.11b),

dcor { dx

dr}

d q/

= r - tar"~ + tax-~

Lewis R.I. Turbomachinery Performance Analysis

Подождите немного. Документ загружается.