Lewis R.I. Turbomachinery Performance Analysis

154

Vorticity production in turbomachines and its influence upon meridional flows

Introducing these results into Eqn (6.26) and rearranging, we have finally an auxiliary

equation for too as follows"

d(cor) r dpo

(6.27)

~o= Co d~ p

dq,

The tangential vorticity too has thus been found to depend entirely upon the

distributions of the two key physical design quantities

(cor),

the angular momentum

and Po, or the stagnation pressure. These are independently conserved along

streamlines as proved in Section 6.3.3 for the annular regions between blade rows.

The levels of

cor

and Po may of course be changed at a blade row as determined

by the Euler pump or Euler turbine equations (1.9) and (1.10), Chapter 1. The actual

vorticity too thus created, however, will depend only upon the gradient of

cor

or Po

across the meridional streamlines

d(cor)/dqJ

and

@o/dO.

For the classic flee-vortex

case as discussed in Section 5.1, Eqn (6.27) reduces to

cor

= constant 1 free-vortex flow

Po = constant J (6.28)

and hence too = 0

Thus for free-vortex turbomachines the governing equation reduces to

o~ 1 O0 o~

Ox 2 r Or

t- --~ = 0 (6.29)

In all other cases the meridional flow for incompressible turbomachines is described

by the combined governing and auxiliary equation (6.21) and (6.27), namely

6.4 Streamwise and smoke-ring vorticity

As revealed by Eqn (6.27) the tangential vorticity too has two independent

components, one produced by gradients of angular momentum

d(cor)/dqJ

and the

other by gradients of stagnation pressure dpo/d~,. These have quite different physical

origins which are illustrated in Fig. 6.6 and consequently have completely different

properties which lead to their respective titles

streamwise

and

smoke-ring

vorticities.

Let us deal with these in turn.

6.4.1 Streamwise vorticity- constant stagnation pressure flows

For constant stagnation pressure flows the equations of motion (6.22) reduce to

OJ x tO r tO 0

.....

(6.31)

C x C r C 0 C

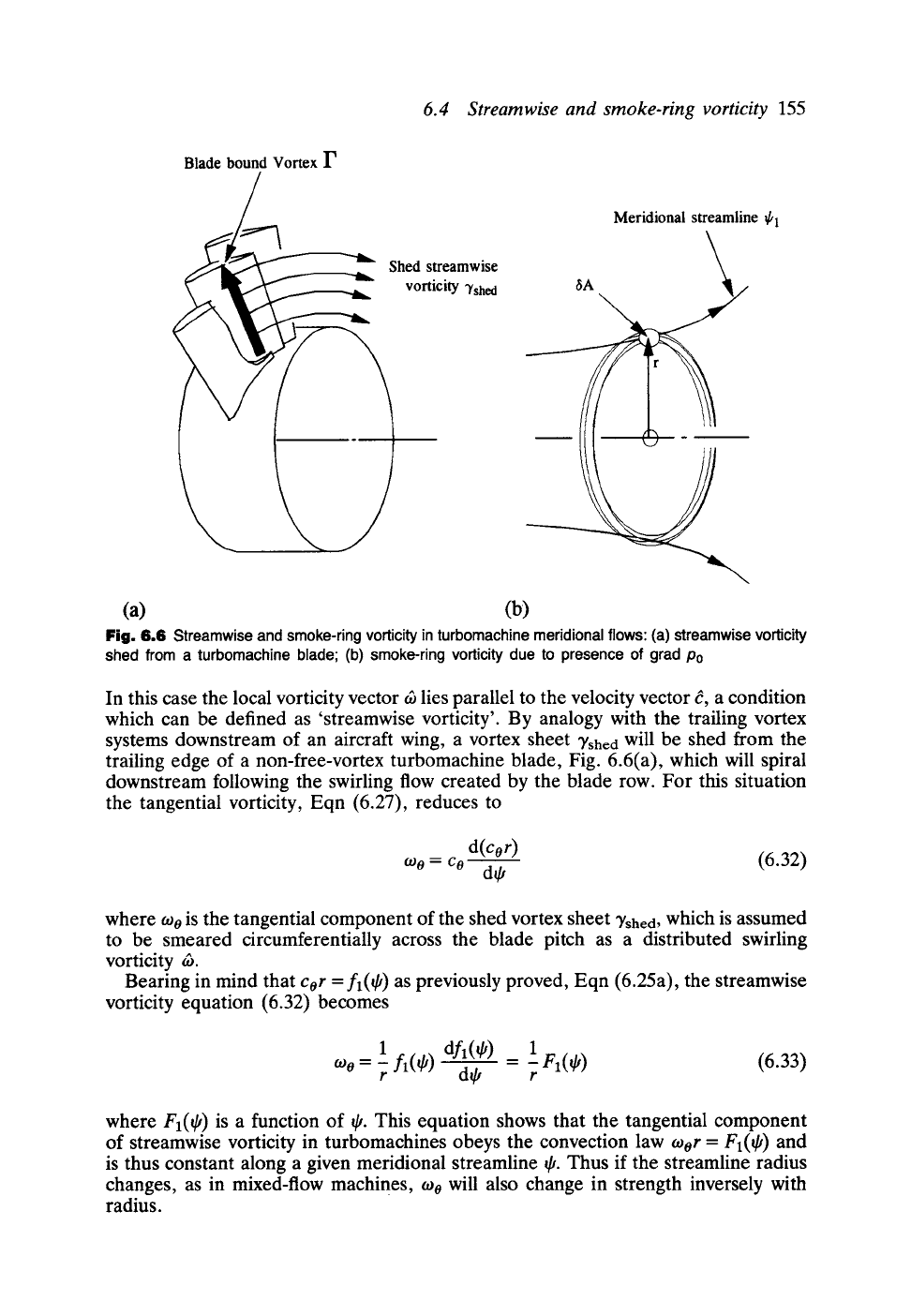
Blade bound Vortex r

6.4

Streamwise and smoke-ring vorticity 155

Shed streamwise

vorticity

"Yshexl

6A

Meridional streamline ~kl

(a) (b)

Fig. 6.6 Streamwise and smoke-ring vorticity in turbomachine meridional flows: (a) streamwise vorticity

shed from a turbomachine blade; (b) smoke-ring vorticity due to presence of grad Po

In this case the local vorticity vector cb lies parallel to the velocity vector d, a condition

which can be defined as 'streamwise vorticity'. By analogy with the trailing vortex

systems downstream of an aircraft wing, a vortex sheet Tshed will be shed from the

trailing edge of a non-free-vortex turbomachine blade, Fig. 6.6(a), which will spiral

downstream following the swirling flow created by the blade row. For this situation

the tangential vorticity, Eqn (6.27), reduces to

d(cor) (6.32)

~oo = Co d~

where ~o0 is the tangential component of the shed vortex sheet Tshed, which is assumed

to be smeared circumferentially across the blade pitch as a distributed swirling

vorticity d~.

Bearing in mind that cor = fl(~') as previously proved, Eqn (6.25a), the streamwise

vorticity equation (6.32) becomes

1 dfx(@) 1

~oo = - fl(~') = - F1(r (6.33)

r d$ r

where FI(~,) is a function of ~,. This equation shows that the tangential component

of streamwise vorticity in turbomachines obeys the convection law ~oor = FI(~,) and

is thus constant along a given meridional streamline ~,. Thus if the streamline radius

changes, as in mixed-flow machines, ~0 will also change in strength inversely with

radius.

156

Vorticity production in turbomachines and its influence upon meridional flows

6.4.2 Smoke-ring vorticity - flee-vortex or non-swirling flows

If either

Co

= 0 or

cor

= constant, the streamwise vorticity is zero and the first term

of Eqn (6.27) vanishes, reducing the tangential vorticity to

rdpo

to0 = (6.34)

p d~

Recalling the conservation law for stagnation pressure from Eqn (6.25b), namely that

Po = f2(~), the above equation becomes

r df2(~ )

too = = - rF2( ~)

(6.35)

p d~

where F2(~,) is a function of ~,. In this case the tangential vorticity obeys a quite

different convection law, namely that to0/r = -F(~), and is thus constant along a given

meridional streamline ~. From the definitions of vorticity components, Eqn (6.11),

it is clear that fox and

tO r

are both zero for the flows presently under consideration.

As the only vorticity component present in the fluid, too takes the form of smoke-ring

vorticity concentric with the x-axis as illustrated in Fig. 6.6(b).

As a check upon Eqn (6.35) we can apply the circulation theorem of Kelvin,

devised in 1869, to this elementary smoke-ring vortex tube of cross-sectional area

8A. As proved by Kelvin the circulation around the perimeter of

6A, w .ds,

which

is defined as the strength of the vortex tube, remains constant as it convects with

the fluid. As previously proved by Helmholtz in 1858, the strength of a vortex tube

also equals the total vorticity flux through its cross-sectional area, in this case

too6A.

Thus by Kelvin's theorem

too6A =

constant (6.36)

These laws apply only to a control mass that contains the same fluid making up an

actual vortex tube. Thus we can also state for incompressible flow that the vortex

tube volume remains constant, namely

2zrr6A

= constant (6.37)

Dividing Eqns (6.36) by (6.37) it follows that to0/r = constant along the drift path

~1 of the vortex tube in agreement with Eqn (6.35).

6.4.3

Axisymmetric flows involving a mixture of both streamwise and smoke-ring

type vorticity components

In general, gradients of both

cor

and Po will be present in turbomachines and the

associated complex vortex motion will comprise both streamwise and smoke-ring

type vorticities. The governing equations for the general turbomachine will then

reduce to

2 1 0r o'2 ,

Ox 2 r Or

~--~-= FI(0)+ r2F2(~ ') (6.38)

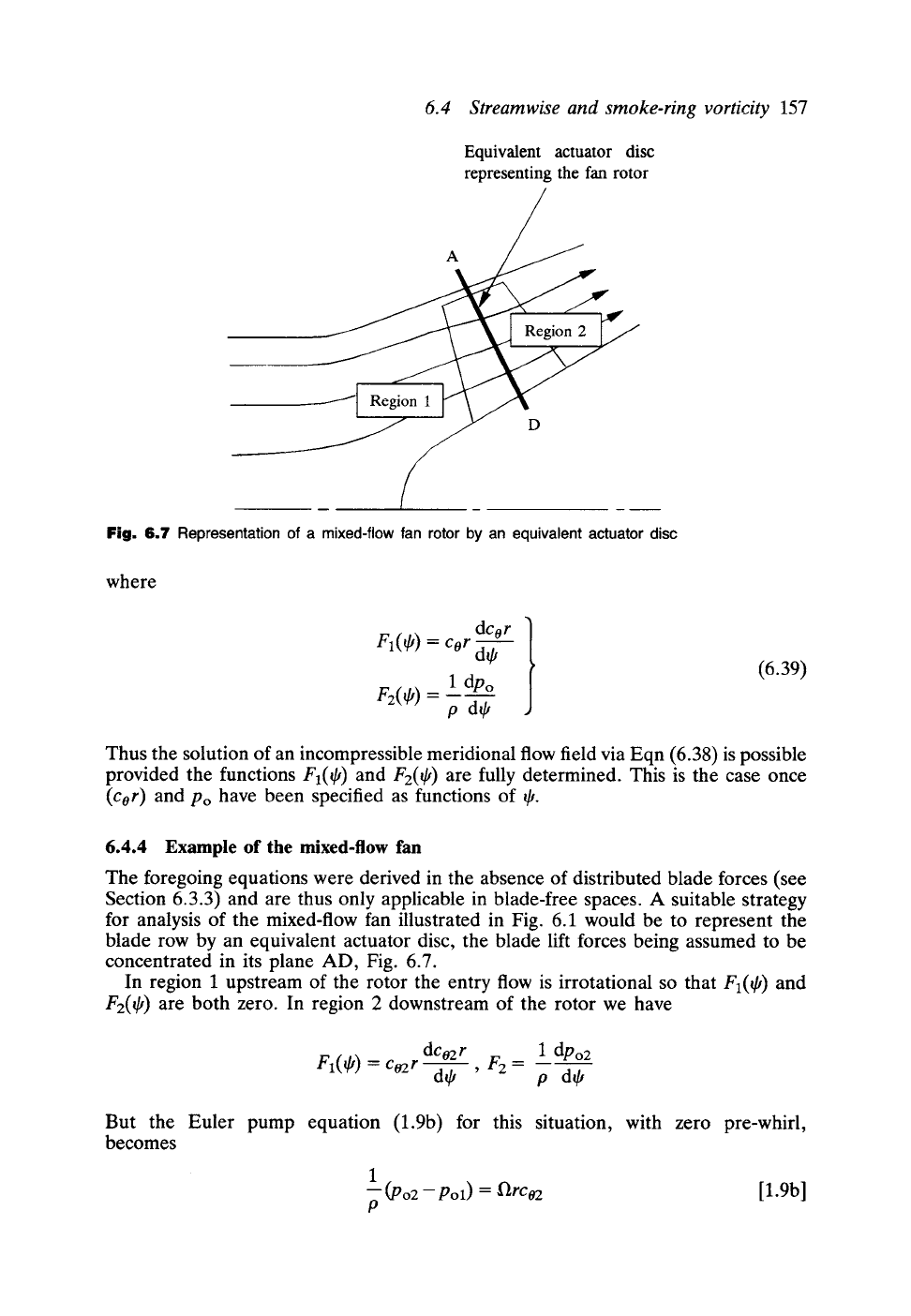
6.4 Streamwise and smoke-ring vorticity

157

Equivalent actuator disc

representing the fan rotor

A

Fig. 6.7 Representation of a mixed-flow

fan rotor by an equivalent actuator

disc

where

dcor

FI(~) =

cor d~

1

dpo

F2(~) = P d~

(6.39)

Thus the solution of an incompressible meridional flow field via Eqn (6.38) is possible

provided the functions FI(~,) and F2(~,) are fully determined. This is the case once

(cor)

and Po have been specified as functions of ~,.

6.4.4 Example of the mixed-flow fan

The foregoing equations were derived in the absence of distributed blade forces (see

Section 6.3.3) and are thus only applicable in blade-free spaces. A suitable strategy

for analysis of the mixed-flow fan illustrated in Fig. 6.1 would be to represent the

blade row by an equivalent actuator disc, the blade lift forces being assumed to be

concentrated in its plane AD, Fig. 6.7.

In region 1 upstream of the rotor the entry flow is irrotational so that FI(~,) and

F2(~,) are both zero. In region 2 downstream of the rotor we have

dCoEr

1

dpo 2

FI(r

= co2r , F2 =

dg, p d$

But the Euler pump equation (1.9b) for this situation, with zero pre-whirl,

becomes

1

--(Po2 -- Pol) =

arco2

[1.9b]

P

158

Vorticity production in turbomachines and its influence upon meridional flows

Equivalent actuator disc

AD

Fig. 6.8

Physical assumption of linearised actuator disc theory

Thus finally the governing equation for the fan problem may be fully stated in terms

of Po2 only through

~g, 1 ag~ oCg,

Or 2 r

Or F

=0

(Po2 --

Pol)/P ) 1

dpo 2

"- ~-~2

+rE p dqJ

Region 1

Region 2

(6.40)

6.5 Analytical solution for linearised cylindrical actuator

disc theory

Early in the history of meridional flow analyses exact solutions to Eqns (6.30) were

obtained by Bragg and Hawthorne (1950) and these have been discussed in full by

Horlock (1978) in his extensive text on actuator disc theory. These solutions formed

a most important benchmark in this subject and the genesis of many of the physical

concepts presented in this chapter. They were, however, restricted to certain classes

of flow and were succeeded by more generally applicable linearised analyses such

as that adopted in the last chapter. The aim in this section is to derive the cylindrical

actuator disc solution from the governing equations (6.38) and (6.39) in linearised

form for flow through a single blade row with the following assumptions:

(1) The blade row is represented by a plane actuator disc at which the vorticity

too is created discontinuously.

(2) The vorticity too is assumed to be convected downstream of the actuator disc

along the undisturbed streamlines.

The terms on the right-hand side of Eqn (6.38) being non-linear presented difficulties

for numerical reduction in the 1950s and assumption (2) provided, in effect, a

linearisation of those terms since the vorticity too could now be approximated as

follows. From Eqn (6.38)

r(oo

= FI(~)+ r2F2(~)

Fl(r) + r2F2(r)

(6.41)

= f(r)

6.5 Analytical solution for linearised cylindrical actuator disc theory

159

For the single blade row depicted in Fig. 6.8 the governing equation (6.36)

simplifies to

s162 1 ar s162 - F(r)

for x>0

0x 2 r Or ~- ~ = (6.42)

=0 for x<0

Since this equation is linear its solution can be compounded from three com-

ponents:

q~ = ~(r) + q/oo(r) + q/(x, r) (6.43)

(a) (b) (c)

where term (a) represents the uniform stream

Cx

at entry to the duct x = -oo, (b)

represents the radial equilibrium flow at exit x = oo, and (c) is a smoothing function

which merges the flow progressively between these two extremes. Equation (6.42)

may now be replaced by three independent equations as follows:

-

- -- + = 0 Uniform stream -~ < x < oo (6.44)

r Or

1 a~

~~ Radial equilibrium

- - -- + = - F(r)

(6.45)

r ar ar 2

perturbation for x > 0

: - tOor

02 q/ Irrotational smoothing

02q/ 1 Oq/ I- =0 (6.46)

OX 2 r

Or

or 2

perturbation for -~ < x < oo

Bearing in mind the definition of stream function, Eqn (6.16a), the first equation

may be integrated once to yield

loaI~

Cx

.... constant (6.47)

r 3r

The second equation (6.45) likewise may be integrated once to give the radial

equilibrium velocity perturbation directly from the specified vorticity tOo:

_ 1 a~" I,~ ~

Cx~ r Or toodr + K

(6.48)

where the constant K is chosen such that the velocity perturbation Cxoo provides no

contribution to mass flow through the annulus, that is

rh t PCx=2'rrr dr = 0

or (6.49)

it .

K = r2 _ r2 r too drdr

160

Vorticity production in turbomachines and its influence upon meridional flows

Thus solutions to Eqns (6.44) and (6.45) have been obtained explicitly in terms of

the specified mean axial velocity

Cx

and tangential vorticity too respectively. The

solution of Eqn (6.46) may be obtained by separation of variables, Hildebrand (1956),

as an infinite series of the following form"

qt' = r ~ An{Jl(knr ) + v n Yl(knr)} e +-k'x

n=l

(6.50)

where

Jl(knr)

and

Yl(knr)

are Bessel functions of the first and second kind of first

order and

An,vn

are arbitrary constants. The coefficients k,, are determined by

specification of zero radial velocity perturbation Cr. Thus from Eqn (6.16b)

p

Cr --

1 0r

r Ox

oo

(+) 2 knAn(Jl(knr) + vn Yl(knr)}

e(+-)~x = 0

n=l

Application of this at hub and tip radii r h and r t for the nth term results in

J1 (kn

rh) +

Vn Y1 (kn

rh) = 0

Jl(knrt) + ~'n Yl(knrt) = 0

and eliminating Un we have

Jl(knrh) Yl(knrt) - Jl(knrt) Yl(knrh) = 0

(6.51)

Solutions of this equation for the coefficients

kn

are given in Table 5.6, Section 5.4,

for hub/tip ratios in the range 0.3 <

rh/r t

< 1.0. The remaining boundary conditions

to be satisfied are as follows.

(1)

Boundary conditions at entry and exit.

For the smoothing perturbation to

vanish at +~ let us propose separate solutions upstream and downstream of

the blade row with the appropriate sign convention as follows:

oo

qt~ = r 2 Anl{Jl(knr) + vn Yl(knr)} ek'x

n=l

oo

d/~ = r 2 An2{Jl(knr) + Vn Yl(knr)} e -knx

n--1

x<0

x>0

(6.52)

(2)

Smooth matching of cr at x = O.

In reality the vorticity too is shed

progressively by the blades from leading edge to trailing edge. For

mathematical simplicity, however, we will replace the blade row by a plane

discontinuity at x = 0 or

actuator disc

at which too is shed discontinuously.

However, although this implies that swirl velocities

co

also change

discontinuously at the actuator disc, the meridional velocity components

Cx

and cr in the

(x,r)

plane develop smoothly over -oo <x < oo. This will be

achieved if the two solutions, Eqns (6.52), are matched at the actuator disc.

Since Cr =-(1/r)(O~/Ox) we have

6.5 Analytical solution for linearised cylindrical actuator disc theory 161

oo

Crl : -- Z knAnl{Jl(knr) + vn Yl(knr)} ek'x

n--1

x_O

oo

' Z knAn2{Jl(knr) + vnYl(knr)} e-k~x x > 0

Cr 2 --

n=l

Matching these two solutions at x = 0 we have

oo oo

-- ~ knAnl{Jl(knr)+ Pn Yl(knr)} = Z knAn2{Jl(knr) + Pn

Yl(knr)}

n=l n=l

This condition is satisfied if, term by term,

Anl = -An2 = A n

whereupon we have finally the solution

OQ

~' = (++_)r Z An{Jl(knr) + Vn Yl(knr)} e (+-)k'x

n=l

(6.53)

with (+) for x < 0 and (-) for x > 0.

(3) Smooth matching of Cx at x = 0. The axial velocity Cx may now be expressed

as

for x<_0

0

Cxl = Cx + 2 An -~r {Jl(knr) + Pn Yl(knr)} e k"x

n--1

oo

Z 0

Cx2 -- C x Jr- Cxoo - An -~r {Jl(knr) + Vn

Yl(k~r)}

e -k~x

for

x >-

0

n=l

(6.54)

Thus matching the upstream and downstream axial velocity solutions at x = 0,

by stating Cxl = Cx2, we have

2 An{Jl(knr) + vn Yl(knr)} ='2 Cx~

n=l

(6.55)

Since Cx~ is a known function of radius once too is prescribed, Eqn (6.48), the

coefficients An, Vn may be derived by Fourier-Bessel analysis term by term.

6.5.1 Simplified actuator disc solution

To avoid the complexity of Fourier-Bessel analysis simple results follow if we assume

that the first term of the Bessel series in Eqns (6.55) predominates. Neglecting all

terms except n = 1 we could approximate Eqn (6.55) as

A l{Ji (kl r) + vl Yi (kl r) } ~- Cxd = 89

162

Vorticity production in turbomachines and its influence upon meridional flows

and thus the solution for

Cx,

Eqns (6.54), reduces to the simple actuator disc

formulation used in Chapter 5, Eqns (5.49) and (5.50)"

Cx

= Cx + lc,xoo e k'x

for x < 0 ]

(6.56)

= Cx +

Cx=(1

-89 -k'x)

for x>0

where the coefficient

k I

is related to the k values listed in Table 5.6 through

kl = k/(rt-

rh).

6.6 Compressible flow actuator disc theory

The first attempt to extend actuator disc theory to compressible flows was published

by Hawthorne and Ringrose (1963). This was followed by a broader-ranging paper

by Lewis and Horlock (1969) which was mainly concerned with the influence upon

meridional flows of blockage due to blade thickness, linking this to compressibility

effects. Appendix 1 of the latter reference contains the basis of a compressible flow

linearised actuator disc theory similar to that to be presented here. Let us begin with

the continuity equation (6.14) for compressible flow and the consequent definition

of Stokes' stream function:

1 ar

Cx = pr Or

1

Oq,

Cr = pr Ox

(6.15)

Introduction of these expressions into the tangential vorticity component too, Eqn

(6.11), results in

O~C r 8C x

too= 8x 8r

Expanding the partial derivatives, this can be rearranged to read as follows:

s162

Ox 2

1 ar

s162

r -~r ~ -~ - P r w ~ - r C r ~x + r C x ~rr

(6.57)

The strategy adopted here has been to separate the Stokes' operator onto the

left-hand side of the equation and to consign all terms involving the density p to the

fight-hand side. These include the following:

(1) Disturbances due to the presence of tangential vorticity too (we note that

these are now weighted by the density p for this case of compressible flow).

(2) Disturbances due to the density gradients

Op/Or

and

Op/Ox.

We will consider

these in more detail in the next section.

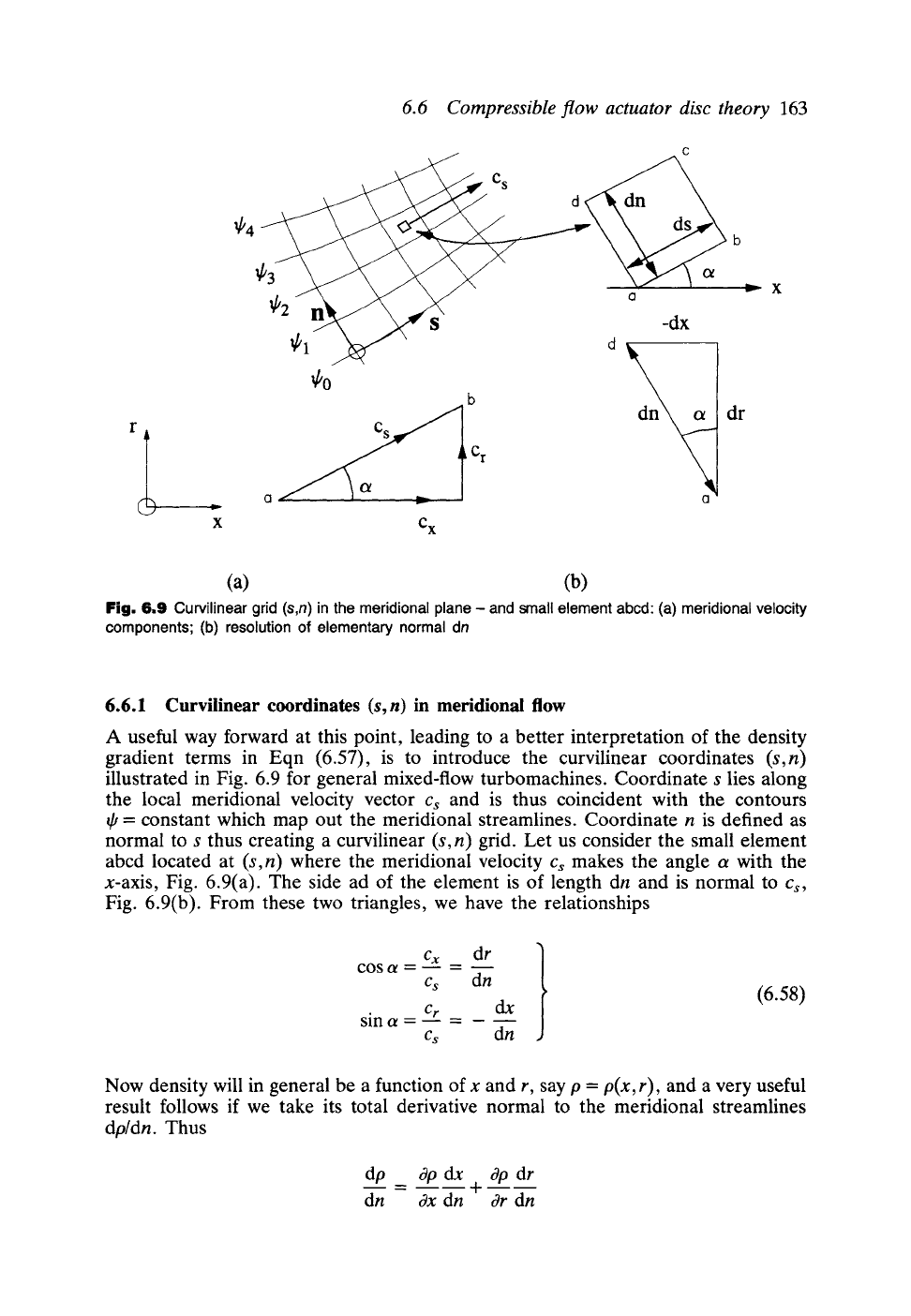
r

6.6 Compressible flow actuator disc theory

163

c

t~4 b

t~2 "- ~

-dx

\ I

dn ~

dr

o

Cr

,...- El

C x

(a) (b)

Fig.

6.9 Curvilinear grid

(s,n)

in the meridional plane - and small element abed" (a) meridional velocity

components; (b) resolution of elementary normal dn

6.6.1 Curvilinear coordinates (s,n) in meridional flow

A useful way forward at this point, leading to a better interpretation of the density

gradient terms in Eqn (6.57), is to introduce the curvilinear coordinates

(s,n)

illustrated in Fig. 6.9 for general mixed-flow turbomachines. Coordinate s lies along

the local meridional velocity vector

Cs

and is thus coincident with the contours

~p = constant which map out the meridional streamlines. Coordinate n is defined as

normal to s thus creating a curvilinear

(s,n)

grid. Let us consider the small element

abcd located at

(s,n)

where the meridional velocity c~ makes the angle a with the

x-axis, Fig. 6.9(a). The side ad of the element is of length dn and is normal to

Cs,

Fig. 6.9(b). From these two triangles, we have the relationships

cosa=Cx

= dr

Cs dn

Cr dx

sin a = ~ =

Cs dn

(6.58)

Now density will in general be a function of x and r, say p =

p(x,

r), and a very useful

result follows if we take its total derivative normal to the meridional streamlines

dp/dn.

Thus

dp 0/9 dx @ dr

dn ax dn ar dn

Lewis R.I. Turbomachinery Performance Analysis

Подождите немного. Документ загружается.