Лесникова Н.П. Физическая химия. Самостоятельное решение задач по химической термодинамике, электрохимии и кинетике
Подождите немного. Документ загружается.

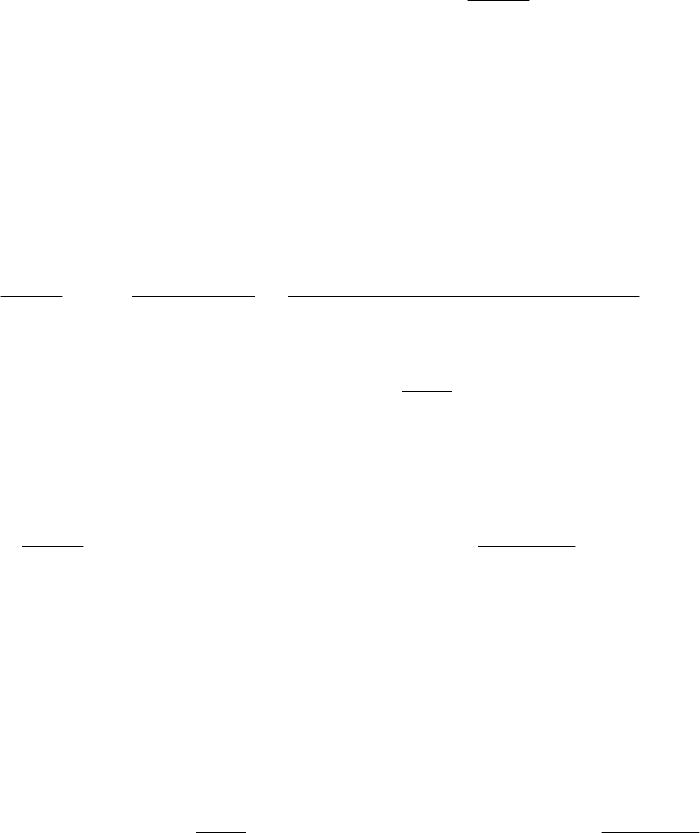
81
1.60. Определить направление процесса при 100 K
,22
2 твгтв
FeOOFe
если при этой температуре
.10026,2;10136.4
4120
2
ПарПаK
Оp
Ответ: – 475 кДж.
Зависимость константы химического равновесия от
температуры (уравнение изобары)
Практика показала, что больше всего константа равновесия за-
висит от температуры. Для вывода воспользуемся уравнениями
Гиббса-Гельмгольца и уравнением изотермы:
.lnln
P
P
P
KRTПRTG
T
G
THSTHG
Выразим частную производную и подставим вместо изменения
энергии Гиббса уравнение изотермы
.lnln
lnln
T
H
KRПR
T
HKRTПRT
T
HG
T
G
PР
PP
P
(1,92)
Продифференцируем по температуре уравнение изотермы
lnR
T
G
P
.
ln
ln
P
P
PР
T
K
RTKRП
(1.93)
Сравним уравнения (1.92) и (1.93); при равенстве левых частей
уравнения равны и правые:
,
ln
lnlnlnln
P
P
PРPР
T
K
RTKRПR
T
H
KRПR

82
после сокращения подобных членов, получим
.
ln
,
ln
22
RT
H
dT
Kd
RT
H
T
K
P
P
P
(1.94)
Последнее уравнение было выведено при постоянном давлении,
поэтому, и называется уравнением изобары
Если реакция протекает при постоянном объеме, то аналогично
можно получить уравнение изохоры:
.
ln
,lnln,
2
RT
U
dT
Kd
KRTПRTA
T
A
TUA
C
CC
V
(1.95)
Анализ уравнения изобары показывает, что зависимость кон-
станты равновесия от температуры (соответственно, знак производ-
ной) определяется знаком теплового эффекта реакции.
Если
0
H
(эндотермический процесс), то первая производ-
ная положительна, 0
ln
dT
Kd
P
. Следовательно, для эндотермиче-
ской реакции с повышением температуры константа равновесия бу-
дет увеличиваться, т.е. химическое равновесие будет смещаться в
сторону продуктов реакции.
При
0
H
(экзотермическая реакция), первая производная
отрицательна, 0
ln
dT
Kd
P
; с повышением температуры константа
равновесия будет уменьшаться, и химическое равновесие будет
смещаться в сторону исходных веществ.
Если
0
Н
, то константа равновесия не зависит от темпера-
туры. Таким образом, уравнение изобары позволяет предвидеть и
оценить (количественно и качественно) зависимость константы рав-
новесия от температуры.
Чтобы определить изменение константы равновесия при изме-
нении температуры на конечную величину, нужно уравнение изоба-
ры (1.96) проинтегрировать:
.lnln,ln
2
B
RT
H
KdT
RT
H
Kd
PP
(1.97)
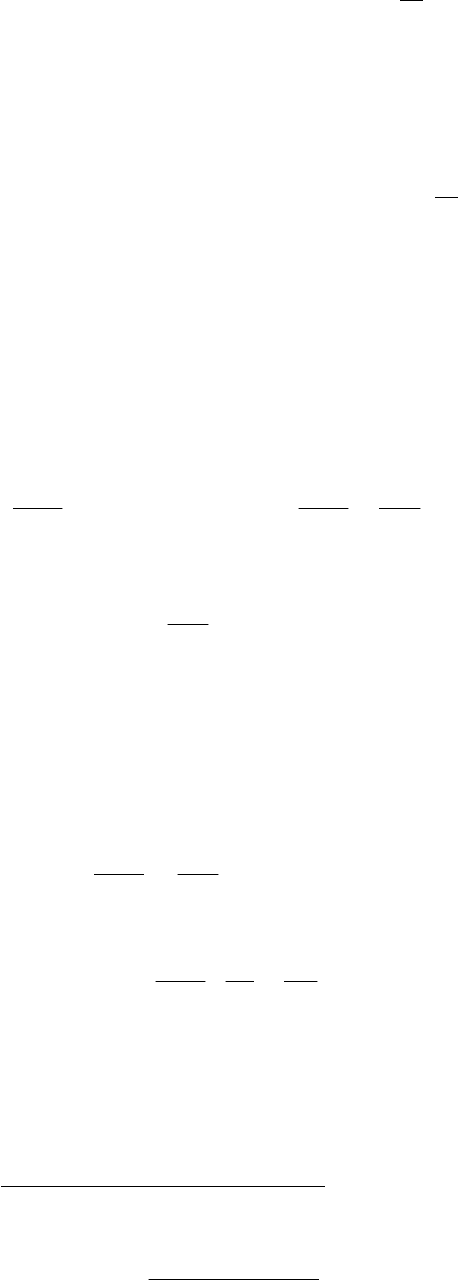
83
Графическая зависимость константы равновесия от темпе-
ратуры (1.97) на графике в координатах
T
fK
P
1
ln
изображается
прямой. Из тангенса угла наклона прямой на этом графике можно
вычислить значение теплового эффекта реакции:
,
Rtg
H
где
– угол наклона линейной зависимости
P
Kln от
T
1
.
Уравнение (1.97) справедливо для достаточно узкого интервала
температур, когда можно приближенно считать
H
постоянной ве-
личиной. В этом уравнении
B
ln
– const интегрирования, ее физиче-
ский смысл после небольших преобразований можно определить:
.ln;ln
;ln;
R
S
RT
H
KS
T
H
KR
STHKRTSTHG
PP
P
(1.98)
Сравнение уравнения (1.97) и уравнения (1.98) показывает, что
.ln
R
S
B
(1.99)
Из этого соотношения можно определить изменение энтропии.
Если принять в уравнении (1.98) тепловой эффект постоянным
и не зависящим от температуры, то интегрирование в пределах от
1
P
K
до
2
P
K
и от
1
T до
2
T приводит к соотношению:
.
11
lnln
;ln
21
2
12
2
1
2
1
TTR
H
KK
T
dT
R
H
Kd
PP
T
T
K
K
P
P
P
(1.100)
Из этого соотношения можно определить тепловой эффект ре-
акции, константу равновесия при любой температуре:
.lnln
;
lnln
1
2
12
12
21
12
12
TT
TTH
KK
TT
KKTTR
H
PP
PP
(1.101)

84
Если известен температурный ряд теплового эффекта химиче-
ской реакции
1320
DTCTBTATEH
T
r
, то после подста-
новки его в уравнение (1.96), можно определить константу равнове-
сия
T
P
K
при любой температуре, если известна хоть одна константа
при любой другой температуре:
.
11
2
2
ln
11
1
ln
,
1
ln
2
2
2
1
2
1
2
212
1
2
21
2
132
2
0
1
2
2
1
2
1
2,
1,
TT
D
TT
C
TTB
T
T
A
TT
E
RK
K
dT
T
DTCTBTATE
R
dT
RT
H
Kd
T
T
T
T
T
T
Tr
K
K
P
T
T
(1.102)
Это уравнение позволяет также получить температурный ряд
константы химического равновесия, после дифференцирование ко-
торого возможно определение теплового эффекта химической реак-
ции при любой температуре Т .
Способы расчета константы химического равновесия
Константу химического равновесия, как уже отмечалось, мож-
но определить из уравнения изотермы или уравнения изобары. Кос-
венный метод основан на том, что если известны по эксперимен-
тальным данным константы равновесия простых реакций (при стан-
дартных условиях), то константа равновесия изучаемой реакции оп-
ределяется комбинацией уравнений (аналогично расчету тепловых
эффектов реакций по закону Гесса), используя свойство энергии
Гиббса (энергии Гельмгольца) как функции состояния.
Для реакции
2
2
2
HCOCOOH
требуется определить
константу равновесия при стандартных условиях. Известно измене-
ние энергии Гиббса для двух реакций, комбинацией которых (вычи-
танием одной из другой), можно получить исследуемую реакцию и,
соответственно, рассчитать константу равновесия:

85
0
2298
0
1298
0
298
0
2298
0
1298
222
0
2298
0
1298
222
0
2298
0
1298
22222
0
2298
222
0
1298
22
2
1
2
1
,
2
1
2
1
2222
2222
22
22
GGG
GGHCOOHCO
GGHCOOHCO
GGOHCOOHOCO
GOHOH
GCOOCO
r
Замена энергии Гиббса (уравнение изотермы) и смена знаков в по-
следнем соотношении, позволяет определить искомую константу
.,)lnln(ln
ln
2
1
ln
2
1
ln
2,298
1,298
298
2
1
2,2981,298298
2,2981,298298
P
P
PPPP
PPP
K
K
KKKK
KRTKRTKRT
Расчет константы равновесия с помощью функций приве-
денной энергии Гиббса. Под стандартным приведенным термоди-
намическим потенциалом (приведенной энергией Гиббса) понимают
функцию
T
HTG
TФ
T
HTG
TФ
298
,
0
00
0
00
0
, (1.103)
где
TG
0
– стандартное значение энергии Гиббса при температуре
Т,
298,0
00
HH – стандартные значения энтальпии при 0 и 298 К
соответственно.
Из соотношения
,
000
TTSTHTG следует, что при
.00,0
00
HGKT Числовые значения
0,0
00
HG неиз-
вестны, поэтому на практике используют разность
,00
0000
HTGGTG которую можно определить экспери-
ментально. В настоящее время функции Ф
0
и Ф
0’
определены при
различных температурах с большой точностью для многих газооб-
разных веществ (состояние идеального газа) по молекулярным по-
стоянным.

86
Для кристаллических веществ расчет Ф
0
основан на использо-
вании на использовании экспериментальных данных для теплоемко-
сти
0
P
C от самой низкой температуры (
K
4
) до текущей темпера-
туры Т. Функция Ф
0
рассчитывается по уравнению:
,0
,
0
0
0
0
0
000
0
0000
0
dT
T
C
TSdTCHTH
TS
T
HTH
T
THTG
TФ
T
P
T
P
которое после преобразований имеет вид
.
1
0
0
0
00
T
P
T
P
dT
T
C
dTC
T
TФ
(1.104)
Значения Ф
0
(Т) приведены в справочниках. Связь между при-
веденным термодинамическим потенциалом реагентов и изменени-
ем стандартной энергии Гиббса при реакции устанавливается сле-
дующим соотношением
,00
0
00
000
00
0000
HTФTH
T
HTG
T
HHTGTG
rrrr
rrrr
(1.105)
где
0
0
H
r
– стандартный тепловой эффект реакции при 0 К. Так
как,
00
ln KRTG
r
, то
.
0
3,2
1
lg
0
00
T
H
TФ
R
K
r
r
(1.106)
Если в качестве базисной температуры выбран не 0 К, а 298 К,
то после соответствующих замен в уравнении (9.36) получим
.
298
3,2
1
298298
3,2
1
lg
0
0
000
0
T
H
TФ
R
T
H
T
HTG
R
K
r
r
r
r
(1.107)

87
Значения высокотемпературных составляющих энтальпии
298
00
HTH и функции
T
HTG
Ф
298
00
0
для большин-
ства веществ приводятся в справочниках.
Точный расчет константы равновесия не всегда целесообразен.
Значение
P
K сильно отличающиеся от 1, и, соответственно, очень
большие положительное и отрицательное значение
0
T
r
G указывают
на сильный сдвиг равновесия к исходным веществам и продуктам
реакции. Этих сведений вполне достаточно для суждения о возмож-
ности и полноте протекания реакции в заданных условиях. Поэтому,
даже грубо приближенный расчет, указывающий на значительное
смещение равновесия в ту или другую сторону, не требует уточне-
ния. Лишь при получении малых по абсолютной величине значений
0
T
r
G , и констант равновесия, близких к 1, необходимо провести
более точные вычисления.
Из существующих способов приближенного расчета константы
равновесия часто используют метод Темкина – Шварцмана. По таб-
личным данным определяют изменение энергии Гиббса (вывод сде-
лан ранее, уравнение 1.66), а уравнение для константы имеет вид
.
3,2
1
lg
2210
0
298
0
298
0
MccMbMaMS
T
H
R
K
r
r
(1.108)
Пример 36. Рассчитать константу равновесия реакции синтеза
метилового спирта при 800 K,
,2
32 гг
ОНСННСО
если при 25
0
С
./1004,31102,10228,15
;/10502,01026,328,27
;/1046,0101,441,28
;1013,4;/44,90
263
253
253
2100
298
3
2
KмольДжТТC
KмольДжТТС
KмольДжТТС
ПаKмолькДжН
ОНСНР
НР
СОР
pr
Решение. Определим по уравнению Кирхгофа тепловой эф-
фект реакции при 800 K:

88
.103700298800
3
1004,31
298
1
800
1
10544,0
298800
2
1058,94
29880069,6790440
1004,31
10544,01058,9469,67
90440
,1004,3110544,01058,9469,67
,
33
6
5
22
3
800
298
26
253
0
800
26253
800
298
0
298
0
800
Дж
dT
Т
ТТ
Н
ТТТС
гдеdTСНН
r
Р
Рrr
Из уравнения изобары (1.101) определим константу равновесия
при 800 K:
.105,1
;
298800
298800
31.8
103700
1013.4ln
lnln
ln
221
800,
10
12
12
0
800
298,800,
12
12
0
800
298,
800,
ПаK
TT
TT
R
H
KK
TT
TT
R
H
K
K
p
r
pp
r
p
p
Пример 37. Давление диссоциации MgCO
3
при 817 K равно
0,996¶10
5
Па, а при 843 K оно равно 1,786¶10
5
Па. Определить тепло-
вой эффект реакции разложения магнезита
,
23 гтв
тв
COMgOMgCO
и рассчитать, при какой температуре давление диссоциации будет
равно 1,013¶10
5
Па.
Решение. Тепловой эффект реакции разложения можно опре-
делить из уравнения изобары (1.101), но для этого надо выразить
константу равновесия гетерогенной реакции:
.
2
COp
PK
Определяем тепловой эффект реакции
0
Н , и затем темпе-
ратуру Т
х
при давлении диссоциации 1,013¶10
5
Па:

89
.111300
813843
10996,0ln10786,1ln84381331,8
ln
55
12
1
2
21
0
Дж
TT
K
K
TTR
H
p
p
.814;
111300
10996,0/10013,1ln81331,8
813
1
,10013.1,
ln
55
5
2
0
121
1
KT
T
ПаKKгде
H
KKTR
T
TT
x
x
Tp
pp
x
x
x
Пример38. Определить тепловой эффект реакции при 1000Κ
,2
2
2
HClClH
если зависимость константы равновесия от температуры для этой
реакции соответствует уравнению:
.9,4
1011,0
10128,0lg312,1
7,9411
lg
2
5
3
T
TT
T
K
p
Решение. Из уравнения изобары (1.101) следует, что
,
ln
20
dT
Kd
TRH
p
следовательно, для определения теплового эффекта реакции необ-
ходимо продифференцировать температурный ряд константы рав-
новесия. Вспомним, что
,
lg
3
,
2
ln
x
x
поэтому
.
1011,0
210128,0
7,9411
3,2
312,1
ln
,9,4
1011,0
10128,0
7,9411
3.2ln312,1ln
3
5
3
2
2
5
3
TT
TdT
Kd
T
T
T
TK
p
p
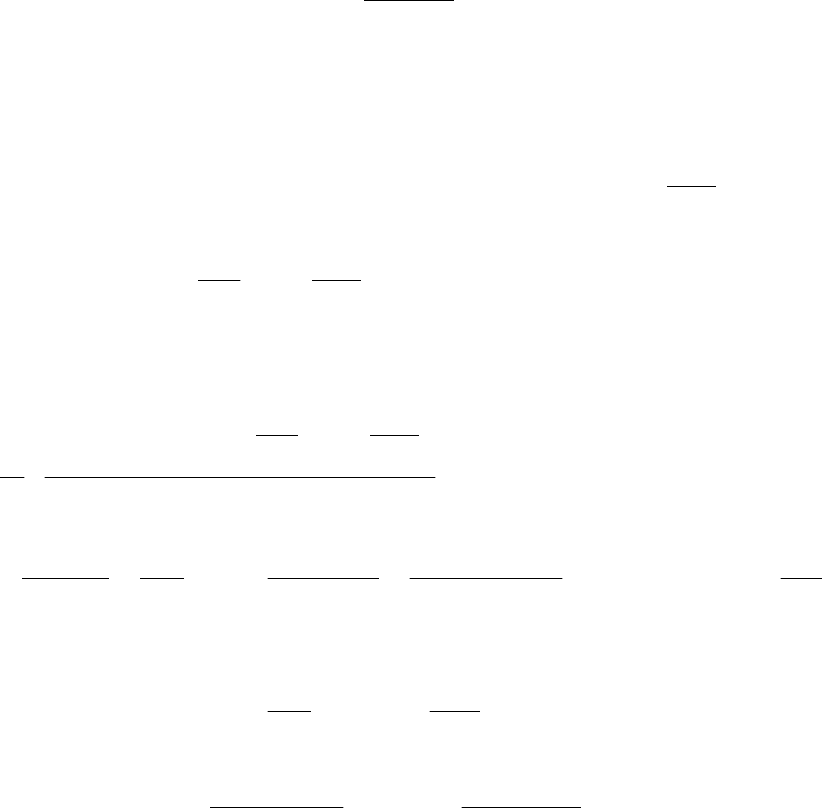
Подставим производную константы равновесия от температу-
ры в уравнение теплового эффекта реакции, тогда
.
1011,0
210128,0
7,9411
3,2
312,1
31,8
3
5
3
2
20
TT
T
TH
90
После сокращения на Т и подстановки в полученное уравнение
Т = 1000 Κ, значение ./1007,189
30
1000
мольДжН
r
Пример 39. Составить уравнение зависимости константы рав-
новесия от температуры с учетом температурного ряда теплоемко-
стей для реакции
2
2
COClClCO
,
если известно, что
.1007,6;1095,6;05,2
;/17,131;112510
53
0
298
0
298
cba
KмольДжSДжH
rr
Решение. Уравнение зависимости константы равновесия от
температуры можно составить в результате интегрирования уравне-
ния изобары:
,ln
2
0
BdT
TR
H
K
Tr
p
где
B
– постоянная интегрирования, а значение
0
T
r
H – тепловой
эффект реакции определяется из уравнения Кирхгофа:
.
2
20
298
2
0
298
298
0
298
0
T
c
T
b
TaH
dT
T
c
TbaHdTCHH
T
r
T
prTr
П
олученное выражение подставим в уравнение зависимости констан-
ты равновесия от температуры и проинтегрируем его:
.
3,2
,
3,22
3,22
lg
3,2
lg
;
2
1
ln
2
0
2
20
В
ВгдеB
TR
c
R
Tb
T
R
a
RT
H
K
BdT
T
T
c
T
b
TaH
R
K
p
p
Вычислим
Н
0
и определим постоянную интегрирования В:
.115457
298
1007,6
298
2
1095,6
29805,2112510
298
298
2
298
5
2
3
2
0
298
0
Дж
cb
aHH
r
