Leroy C., Rancoita P.-G. Principles Of Radiation Interaction In Matter And Detection

Подождите немного. Документ загружается.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

60 Principles of Radiation Interaction in Matter and Detection

βγ, in [Bichsel (1988)] and in Section 27 (Figures 27.7 and 27.8) of [PDB (2008)]

(for a review of experimental data, see Tables VIII and IX in [Bichsel (1988)]).

As an additional example, we can estimate the most probable energy-loss of

spallation protons ²

mp,p,Si

in silicon detectors. These protons, generated by hadronic

interactions in matter, come out of the target nucleus and typically have momenta

between ≈ 500 and 1500 MeV/c, (i.e., kinetic energies between ≈ 125 and 831 MeV;

β and γ values between 0.47 and 0.85, and 1.13 and 1.89 respectively). Furthermore,

the density-eﬀect factor δ, given by Eq. (2.22), is lower than 0.1 and can be neglected

along with the shell correction factor U. By using Eq. (2.17) and approximating

∗

f(², x)

with f(², x)

(Sect. 2.1.2.2), we can rewrite Eq. (2.48) as:

mp,p,Si

= ξ

+ β

+ ln

+ 1− C

+ ln

2mv

(1 − β

)

− 2β

− δ− U

= ξ

ln(ξβ

) + ln

2mc

− β

+ ln γ

+ 0.194

= ξ

ln(ξβ

) + 17.54 − β

+ ln γ

[MeV], (2.51)

where ξ is in MeV and I is given in Table 2.1. Note that, using a Landau function,

the most probable energy-loss

††

is varied by about or less than a percent in the range

of incoming proton momenta from 500 up to 1500 MeV/c for ξ/W

≤ 0.05. By ave-

raging the term (ln γ

−β

) over this range of incoming proton momenta, Eq. (2.51)

can be rewritten, within an additional few % approximation, as:

mp,p,Si

= ξ

ln(ξβ

) + 17.84

[MeV]. (2.52)

It has to be noted [see Eq. (2.41)] that the term ln(ξβ

) does not depend on the

proton momentum. ²

mp,p,Si

has a ln x dependence and goes as 1/β

2.1.2.4 Improved Energy-Loss Distribution and Distant Collisions

The Landau–Vavilov solutions of the transport equation were derived under the

assumption that scatterings occur on quasi-free electrons, and follow the Rutherford

collision probability [Eq. (2.39)]. Therefore, as previously discussed, they neglect the

electron binding energies. But this latter assumption is a valid approximation only

for close collisions.

In general, the distant collisions have also to be taken into account. Modiﬁca-

tions

‡‡

were proposed to the Landau–Vavilov energy straggling function ([Blunck

and Leisegang (1950); Shulek et al. (1966)], see also [Fano (1963); Bichsel and Yu

∗

The reader can see [Seltzer and Berger (1964)] for a tabulation of ²

mp,p

in Vavilov’s theory and,

thus, for estimating its variation with respect to that in Landau’s theory.

††

The energy straggling distribution measured with 37 MeV protons in 10 cm pathlength of argon

at a pressure of 1.2 atmospheres indicates that the most probable energy-loss is a few percent larger

than that calculated using the Landau–Symon [Gooding and Eisberg (1957)] and Vavilov [Seltzer

and Berger (1964)] approaches.

‡‡

Other approaches related photon absorptions or resonant excitations in silicon to the ionization

cross section (e.g., see [Hall (1984); Bak, Burenkov, Petersen, Uggerhøj, Møller and Siﬀert (1987)].

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 61

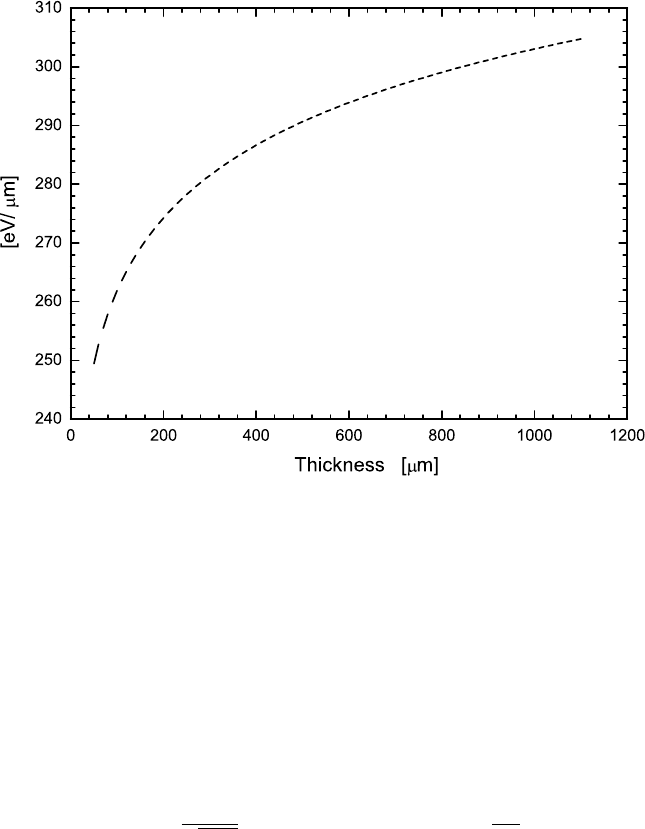
Fig. 2.10 The most probable energy-loss in silicon, calculated by means of Eq. (2.50), divided by

the absorber length (in eV/µm) is shown as a function of the absorber thickness (in µm).

(1972); Bichsel and Saxon (1975); Rancoita and Seidman (1982); Hancock, James,

Movchet, Rancoita and Van Rossum (1983); Rancoita (1984)]). In these approaches,

the Rutherford distribution is replaced by a realistic diﬀerential collision probability

(², E). For close collisions, it has the property that ω

(², E) → ω(², E)

but, at

low transferred energies, it takes into account that the atomic shell structure aﬀects

the interaction. By exploiting the convolution properties of the Laplace transforms

(see [Bichsel and Yu (1972); Bichsel and Saxon (1975)] and references therein), it

was derived that the transport equation solution [Eq. (2.40)] is given by:

f(², x)

√

2πδ

+∞

−∞

f(² − ²

, x)

L,V

exp

−

2δ

d²

, (2.53)

where δ

= M

− M

2,R

is the square of the standard deviation σ

of the Gaussian

convolving distribution, and M

and M

2,R

are the second moments of the realistic

and Rutherford diﬀerential collision functions, respectively. The second moment M

is deﬁned by:

∞

ω(², E) d².

It was shown [Bichsel (1970)] that adding further moments to this correction pro-

cedure does not appear to be needed.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

62 Principles of Radiation Interaction in Matter and Detection

g /cm

W/Emp

0.0001 0.001 0.01 0.1 0.5

0.1

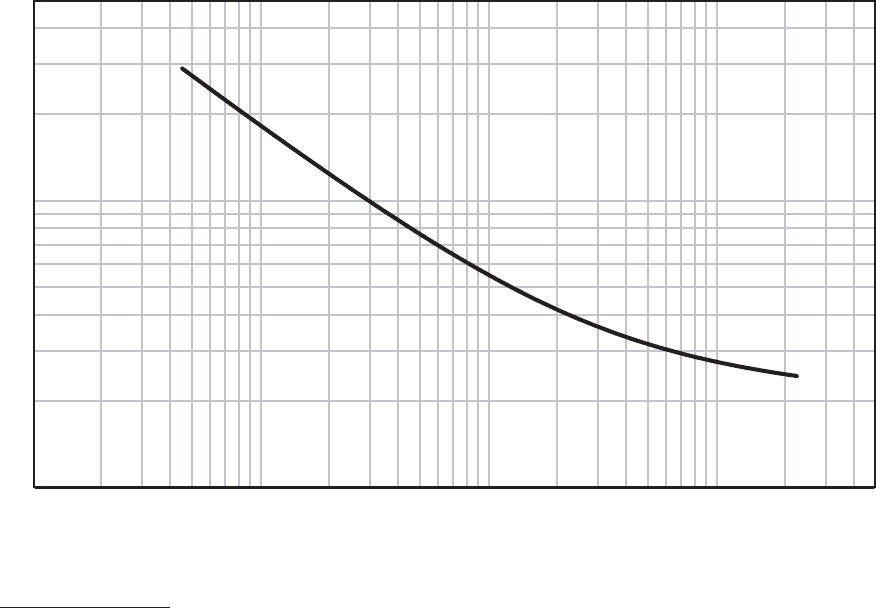
Fig. 2.11 The ratio of F W HM

over the most probable energy-loss (W/E

) versus the thickness χ in units of g/cm

for silicon. F W HM

was

computed as ≈

F W HM

+ F W HM

; the most probable energy-loss (for β = 1) is from Eq. (2.50) and is increased by ≈ 3% to take into account

the eﬀect of the Gaussian folding distribution for the improved energy-loss distribution (as discussed at page 67).

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 63

The functionf (², x)

is called generalized energy-loss distribution or improved

energy-loss distribution (see [Møller (1986); Bichsel (1988)] and references therein

for other approaches for the modiﬁed straggling function).

To a ﬁrst approximation, the value of σ

can be calculated by the Shulek expres-

sion [Shulek et al. (1966)]:

≡

2mc

[MeV], (2.54)

where I

is the excitation energy (i.e., the absorption edges for the various shells

(or subshells) of the element) of the ith shell (or subshell), and Z

is the number of

electrons in the ith shell (or subshell). The summation is carried out over those shells

for which I

< 2mc

. These excitation energies are given in standard tabulations

(see for instance [Carlson (1975)]) and are used to determine the eﬀective excitation

energies (see [Sternheimer (1966, 1971)]), which allow the calculation of the density-

eﬀect correction [Eq. (2.1)]. The value σ

increases as ln β

and becomes almost

constant for β → 1. In addition, σ

varies as

√

x, where x is the absorber thickness

[see Eq. (2.41)]. Comparisons with experimental data are shown in [Hancock, James,

Movchet, Rancoita and Van Rossum (1983, 1984); Rancoita (1984)] and reported

in Sect. 2.1.2.5.

In Eq. (2.53), the resulting improved energy-loss distribution has an overall

value of F W HM

, which is roughly given by

F W HM

+ F W HM

, where

F W HM

' 4.02 ξ varies as x, and F W HM

' 2.36 σ

varies as

√

x. F W HM

and

F W HM

are the FW HM ’s of the energy straggling distribution [f(² − ²

, x)

L,V

]

and of the Gaussian convolving distribution, respectively. As the material thick-

ness decreases, σ

becomes more and more the dominant term, which determines

the overall F W HM

of the straggling function. Conversely, it is not expected to

provide an additional broadening of the distribution at large thicknesses.

For a silicon absorber and using the excitation energies given in [Sternheimer

(1966)], we get [Hancock, James, Movchet, Rancoita and Van Rossum (1983, 1984)]:

I,Si

2mc

+ 2

ln β

)

ξ (2.319 + 0.670 ln β) 10

−3

[MeV], (2.55)

where the excitation energies are those for the K, L, M

(3s) and M

(3p) elec-

trons. As an example, in 300 µm thick silicon detector we ﬁnd F W HM

≈ 21.5

keV, F W HM

≈ 13.6 keV, and an overall F W HM

≈ 25.4 (i.e., 18% larger than

F W HM

) for a relativistic β ' 1 and z = 1 particle. This is in agreement with

the experimental data (see Sect. 2.1.2.5). However, the overall F W HM

value is

almost determined by that of F W HM

for detectors

‡‡

with a silicon thickness

‡‡

It was observed with plastic scintillators 4 and 10 cm thick [Asano, Hamasaki, Mori, Sasaki,

Tsujita and Yusa (1996)].

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

64 Principles of Radiation Interaction in Matter and Detection

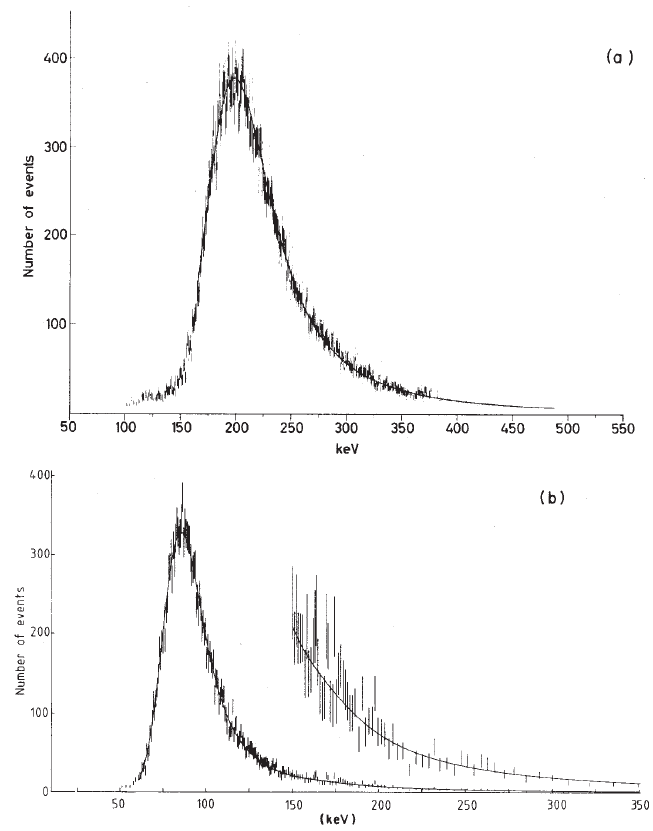
Fig. 2.12 Curves (a) and (b) (adapted and republished with permission from Hancock, S., James,

F., Movchet, J., Rancoita, P.G. and Van Rossum, L., Phys. Rev. A 28, 615 (1983); Copyright

(1983) by the American Physical Society) show the energy-loss spectra at 0.736 and 115 GeV/c of

incoming particle momentum. Continuous curves are the complete ﬁt to experimental data, i.e.,

the Landau straggling function folded over the Gaussian distribution taking into account distant

collisions.

& 1 mm (i.e., & 0.233 g/cm

In Fig. 2.11, the ratio W/E

of F W HM

over the most probable energy-loss

) is shown as a function of χ = xρ in units of g/cm

, for a z = 1 and β = 1

massive particle traversing a silicon medium. The most probable energy-loss E

was computed by means of Eq. (2.50) and increased by ≈ 3% (see page 67) to take

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 65

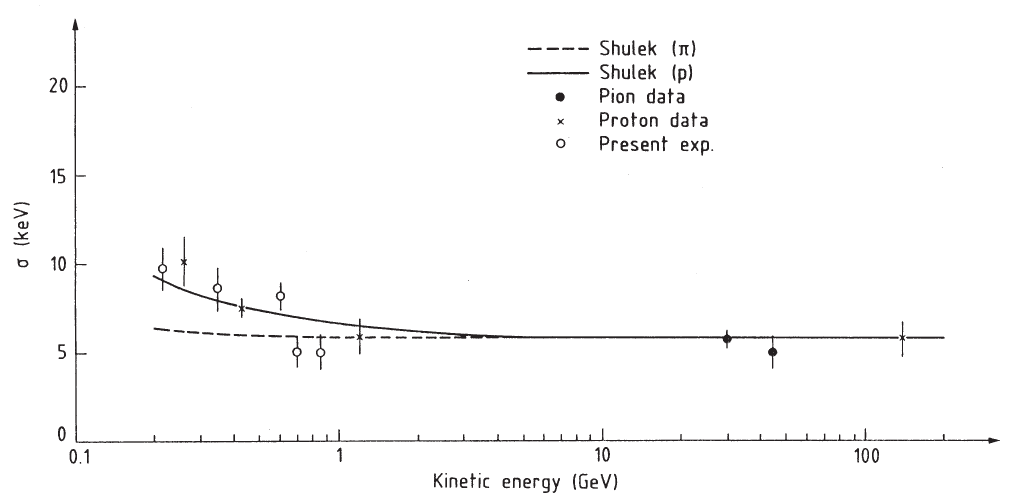
Fig. 2.13 σ

as function of the incoming particle energy (reprinted from Nucl. Instr. and Meth. in Phys. Res. Section B1, Hancock, S., James,

F., Movchet, J., Rancoita, P.G. and Van Rossum, L., Energy-Loss Distributions for Single and Several Particles in a Thin Silicon Absorber, 16–22,

Copyright (1984), with permission from Elsevier). The experimental data are for pions and protons and are compared with the Shulek expression

[Eq. (2.55)].

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

66 Principles of Radiation Interaction in Matter and Detection

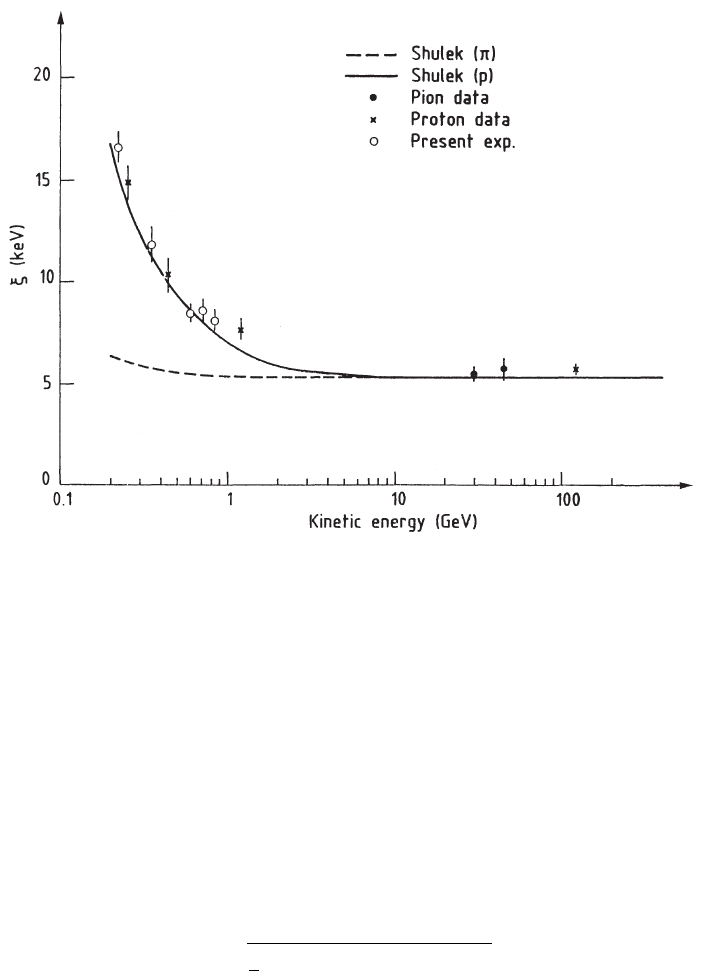
Fig. 2.14 ξ values are shown as function of the incoming particle energy (reprinted from Nucl.

Instr. and Meth. in Phys. Res. Section B1, Hancock, S., James, F., Movchet, J., Rancoita, P.G.

and Van Rossum, L., Energy-Loss Distributions for Single and Several Particles in a Thin Silicon

Absorber, 16–22, Copyright (1984), with permission from Elsevier): the experimental data are for

pions and protons and are compared with values calculated from Eq. (2.41).

into account the eﬀect of the Gaussian folding function of the improved energy-loss

distribution. For very small silicon thicknesses χ ≈ 2 ×10

−3

g/cm

(i.e., equivalent

to ≈ 1.2 cm of Ar at Standard Temperature and Pressure, STP) the values of

W/E

is ≈ 1.2, while for a typical silicon detector thickness of 300 µm (χ = 0.07)

W/E

≈ 0.29.

Furthermore, the ratio W/E

also depends on material-related parameters like

hν

[see Eq. (2.49)] and I [see Eq. (2.54)]. For instance for Ar, using the excitation

energy given in [Sternheimer (1971)], we obtain:

I,Ar

ξ (3.202 + 0.983 ln β) 10

−3

[MeV]. (2.56)

For a z = 1 and β = 1 massive particle traversing a Ar medium at STP, the expected

ratio W/E

is ≈ 0.95, at χ ≈ 2×10

−3

g/cm

. This value agrees with that observed

for Ar gas medium [Walenta, Fisher, Okuno and Wang (1979)].

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 67

2.1.2.5 Distant Collision Contribution to Energy Straggling in Thin Sili-

con Absorbers

In thin silicon detectors, deviations from the Landau–Vavilov energy straggling

distribution were observed [Esbensen et al. (1978)], systematically studied [Hancock,

James, Movchet, Rancoita and Van Rossum (1983, 1984)] up to high energy, and

interpreted as due to the distant collisions which were neglected in the Landau–

Vavilov theories for thin absorbers (see also [Bak, Burenkov, Petersen, Uggerhøj,

Møller and Siﬀert (1987); Bichsel (1988)]).

These systematic measurements were performed using silicon detectors. In this

way, a precise energy determination of the parameters ξ, σ

, and ²

could be

carried out over a large range of proton incoming momenta, from 736 MeV/c

up to 115 GeV/c [Hancock, James, Movchet, Rancoita and Van Rossum (1983,

1984)]. Data were also taken with pions [Hancock, James, Movchet, Rancoita and

Van Rossum (1983, 1984)].

In Fig. 2.12, proton spectra at 736 MeV/c and 115 GeV/c incoming momenta are

shown. The continuous curves are from Eq. (2.53), namely for a Landau straggling

function convolved with a Gaussian distribution. These curves allow the determi-

nation of ξ, σ

, and ²

mp,Si

parameters by a ﬁtting procedure. At high energies,

the agreement with the data is very accurate. It can be partially seen by the mag-

niﬁcation of the Landau tail in Fig. 2.12(b). In Fig. 2.12(a), the data fall below

the expectation curve from above ≈ 450 keV, that is, above this threshold value of

deposited energy, the Landau and Vavilov functions might exhibit a diﬀerence. In

fact, fast δ-rays can also escape from the 300 µm thick silicon detector causing a

decrease of the deposited energy. This eﬀect is not taken into account by Eq. (2.46)

and, consequently, by Eqs. (2.42, 2.45).

The ﬁtted values of ²

are well in agreement with the values expected from

Eq. (2.48). But the eﬀective most probable energy-loss of the curve resulting from

the convolution, i.e., the improved energy-loss curve, is larger than ²

(i.e., the

Landau energy-loss peak) by ≈ 3% [Hancock, James, Movchet, Rancoita and Van

Rossum (1983, 1984)]. This is because the Landau function is asymmetric and, when

convolved with a symmetric (Gaussian) function, the net result is a light shift of

the distribution peak to larger values.

In Fig. 2.13, the σ

I,Si

values are shown: the experimental data are for pions

and protons and are compared with the Shulek expression. Within the experimental

errors, it is seen that the data and the predictions from Eq. (2.55) agree. In addition,

at high energies σ

I,Si

becomes constant as expected.

In Fig. 2.14, the ξ values are shown as a function of the incoming energy: the

experimental data are for pions and protons, and are compared with values calcu-

lated from Eq. (2.41). This general agreement indicates that the energy calibration

was correctly performed and that Eq. (2.53) correctly takes into account both the

close and distant collision contributions to energy-loss ﬂuctuations in thin absorbers.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

68 Principles of Radiation Interaction in Matter and Detection

2.1.2.6 Improved Energy-Loss Distribution for Multi-Particles in Silicon

To a ﬁrst approximation, by assuming that collision losses are statistically inde-

pendent, n

particles with the same velocity βc traversing a thin absorber x will

undergo an overall energy-loss equivalent to the one of a single particle with velocity

βc traversing a thin absorber (x

) n

times thicker, i.e.,

= n

As previously discussed, the energy-loss distribution for a single particle depends

on parameters (i.e., ξ [see Eq. (2.41)], σ

[see Eq. (2.54)] and ²

[see Eq. (2.48)]),

which are functions of the absorber thickness x

. Similarly, the energy-loss distri-

bution for n

particles simultaneously crossing the absorber thickness x depends on

the corresponding parameters ξ

, σ

I,np

, and ²

mp,np

For n

particles traversing an absorber thickness x, we can rewrite Eq. (2.41)

as:

= 0.1535 x

ρz

Aβ

= n

ξ [MeV]. (2.57)

Equation (2.54) is rewritten as:

I,np

≡

2,np

2mc

[MeV]. (2.58)

For silicon absorbers, Eq. (2.58) becomes

I,np, Si

(2.319 + 0.670 ln β)10

−3

[MeV], (2.59)

instead of Eq. (2.55) which is valid for a single particle.

Similarly, Eq. (2.48) has be used for calculating the most probable energy-loss

of a single particle traversing an absorber n

times thicker. At high energies for

β ≈ 1 and βγ > 10

(the parameters S

are given in Tables 2.1 and 2.2), i.e., when

Eq. (2.49) replaces Eq. (2.48), we have:

mp,np

= ξ

2mc

(hν

)

+ 0.194

= n

2mc

(hν

)

+ ln n

− ln n

+ 0.194

= n

2mc

(hν

)

+ ln n

+ 0.194

= n

(²

+ ξ ln n

) [MeV]. (2.60)

Equation (2.60) shows that the most probable energy-loss for a set of n

particles

has a ln n

dependence.

This set of Eqs. (2.57, 2.58, 2.60) has to be employed for the identiﬁcation of

the multiplicity of relativistic particles by means of energy loss.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 69

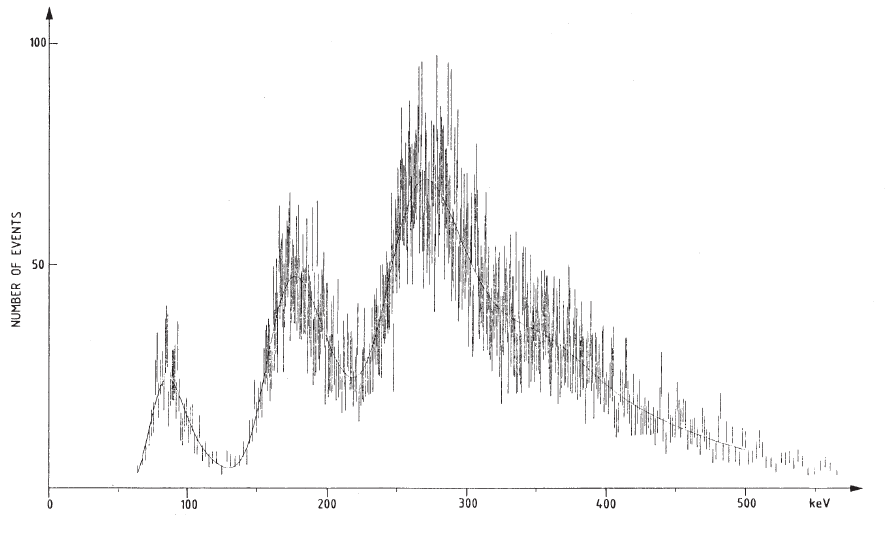
Fig. 2.15 Energy-loss of a relativistic multi-particle production (reprinted from Nucl. Instr. and Meth. in Phys. Res. Section B1, Hancock, S.,

James, F., Movchet, J., Rancoita, P.G. and Van Rossum, L., Energy-Loss Distributions for Single and Several Particles in a Thin Silicon Absorber,

16–22, Copyright (1984), with permission from Elsevier). The ﬁt to experimental data is obtained by assuming Eqs. (2.57, 2.59, 2.60) for the

energy-loss distribution.