Leroy C., Rancoita P.-G. Principles Of Radiation Interaction In Matter And Detection

Подождите немного. Документ загружается.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

30 Principles of Radiation Interaction in Matter and Detection

of the violation of non-ionizing energy-loss (NIEL) scaling. This scaling property,

which expresses the proportionality between NIEL-value and resulting damage ef-

fects, is violated for low energy (. 10 MeV) protons.

Integrated radiation dose delivered by a high particle ﬂux may permanently

damage silicon detectors and electronics. This is a total dose eﬀect which leads

to degradation due to displacement damage and particle interaction and is re-

viewed in the chapter on Displacement Damage and Particle Interactions in Silicon

Devices, where features (under large irradiations) of VLSI bipolar transistors are

treated. These devices are mostly aﬀected by the displacement damage generated

by non-ionizing energy-loss processes. For instance, at large cumulative irradiation

this mechanism was found to be responsible i) for the decrease of the gain of bipo-

lar transistors mostly as a result of the decrease of the minority-carrier lifetime in

the transistor base and ii) for the degradation of the series-noise performance of

charge-sensitive-preampliﬁers with bipolar junction transistors in the input stage,

mainly because of the increase of the base spreading-resistance. The gain degrada-

tion depends almost linearly on the amount of the displacement damage generated

(e.g., the amount of energy deposited by NIEL processes) independently of the type

of incoming particle, thus following an approximate NIEL-scaling.

However, temporary or permanent damage may be inﬂicted by a single particle

(single event eﬀect - SEE) to electronic devices or integrated circuits. Chapter 7

contains also a large section on temporary and permanent damage inﬂicted by a

single particle (single event eﬀect) to electronic devices or integrated circuits. The

generation of SEE in the various radiation ﬁeld environments, and calculation of

their rate of occurrence using data and simulation techniques are outlined. It is

also emphasized that the understanding of radiation eﬀects (not only SEE) on the

silicon devices combined with simulation techniques has an impact on device design

and allows the prediction of the behavior of speciﬁc devices, when exposed to a

radiation ﬁeld of interest. On several occasions, emphasis is put on the fact that the

understanding of the principles of radiation eﬀects on silicon devices combined with

simulation techniques has an impact on device design and allows one to predict the

behavior of speciﬁc devices in radiation environments.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Chapter 2

Electromagnetic Interaction of Radiation

in Matter

The study of radiation detection requires a deep understanding of the interaction of

particles and photons with matter, where they deposit energy via electromagnetic

or nuclear processes. As a result of such processes, a fraction

‡‡

of the incoming

particle energy is released inside the medium. However, there are detectors, like

the so-called calorimeter detectors, in which almost the whole particle energy is

degraded and deposited via a series of successive electromagnetic and/or nuclear

processes.

Inside matter, any type of moving charged particle (α-particle, p, K, π, µ, e,

etc) will lose energy. Particles heavier than electrons will undergo energy losses

mainly due to the excitation and ionization of atoms of the medium, close to their

trajectory. With increasing energy, some of scattered electrons can escape from the

(thin) absorb er or detecting medium. Thus, the deposited energy may be smaller

than the energy lost by a charged particle. For heavy ions, with velocity of the

order (or lower) of the Bohr orbital velocity

††

of electrons in the hydrogen atom,

the energy loss due to collisions with target nuclei is no longer negligible. Electrons

(and positrons) can also lose energy by radiating photons. This latter process is

dominant above the so-called critical energy.

Photons can be fully absorbed by matter in a single scattering or by a few sub-

sequent interactions. Emerging electrons will mainly experience collision losses at

suﬃciently low energy (i.e., below the critical energy) or will radiate other pho-

tons. The most relevant processes for photon absorption in matter are the photo-

electric, Compton and pair production of electrons and positrons.

In this chapter, we will discuss the various electromagnetic processes which take

place when charged particles - electrons, light and heavy ions, etc. - or photons pass

through matter, while in the next chapter nuclear interactions will be considered;

for convenience, the units are expressed in cgs esu and e is the electron charge if

not otherwise explicitly indicated.

‡‡

In (fast) particle detectors, the deposited energy is, usually, a small fraction of the incoming

particle energy.

††

The reader can see page 74 for a discussion on the Bohr orbital velocity.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

32 Principles of Radiation Interaction in Matter and Detection

2.1 Passage of Ionizing Particles through Matter

Charged particles passing through matter lose their kinetic energy by dominant elec-

tromagnetic interactions which consist of excitation

∗

and ionization

†

atoms along

their passage. This process is usually called collision loss process or collision pro-

cess

‡

. Subsequent collision processes mediated by the electromagnetic ﬁeld asso-

ciated with charged incoming particles and medium targets (i.e., bound electrons

and nuclei) lead to the formation of the primary ionization. Fast electrons resulting

from ionization processes are called δ-rays (Sect. 2.1.2.1).

If suﬃciently energetic, these electrons will also excite and ionize atoms. Thus,

a secondary ionization process will take place. However, the deposited energy per

unit path inside the medium is usually lower than the energy lost by collisions,

because the fastest δ-rays can be completely absorbed far away from where they

were generated or escape from the medium.

Furthermore, deﬂections from the incoming direction are usually small, but be-

come relevant in the ﬁnal stage of fully absorbing processes. It has to be noted that

a detailed energy-loss computation for a charged particle traversing a medium is

beyond the scope of this book and can be found, for instance, in [ICRUM (1993a,

2005)] (e.g., see also databases available on web in [Berger, Coursey, Zucker and

Chang (2005)]).

2.1.1 The Collision Energy-Loss of Massive Charged Particles

The collision process induced by massive charged particles (i.e., particles with rest

mass much larger than the electron mass) was studied by Bohr (1913), Bethe (1930),

Bloch (1933) and others [Møller (1932); Williams (1932); Heitler (1954); Stern-

heimer (1961); Andersen and Ziegler (1977); Ahlen (1980); Lindhard and Sørensen

(1996); Sigmund (1997)] (see also references therein). For an incoming particle of

mass m

, velocity v = βc , charge number

††

z and, thus, charge ze, the theoreti-

cal expression for the energy loss by collision, dE/dx, is given by the energy-loss

formula:

−

2πnz

2mv

(1 − β

)

− 2β

− δ − U

, (2.1)

where m is the electron mass (as will be indicated throughout this chapter instead

of the usual notation m

); n is the number of electrons p er cm

of the traversed

material, I is the mean excitation energy of the atoms of the material, W

is the

∗

These are electron transitions from their initial states to higher discrete bound states.

†

These are electron transitions from their initial states to states in the continuum, where electrons

are no longer bounded.

‡

The process is also termed electronic energy-loss, e.g., see Sects. 2.1.4, 4.2.1.1 and Chapter 3

of [Ziegler, Biersack and Littmark (1985a); Ziegler, J.F. and M.D. and Biersack (2008a)].

††

The charge number is the coeﬃcient that, when multiplied by the elementary charge, gives the

charge of an incoming particle [Wikipedia (2008a)], i.e., it is the atomic number of the fully-ionized

incoming particle.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 33

Fig. 2.1 The impact parameter b is the minimum distance between the incoming particle and the

target by which it is scattered.

maximum transferable energy from the incident particle to atomic electrons, δ is

the correction for the density-eﬀect, and ﬁnally U is the term related to the non-

participation of electrons of inner shells (K, L, . . .) for very low incoming kinetic

energies (i.e., the shell correction term). The number of electrons per cm

(n) of

the traversed material is given by (ZρN )/A [Eq. (1.40)], where ρ is the material

density in g/cm

, N is the Avogadro number (see Appendix A.2), Z and A are the

atomic number (Sect. 3.1) and atomic weight (see page 14 and Sect. 1.4.1) of the

material, respectively. The atomic number Z is the number of protons inside the

nucleus of that atom.

The minus sign for dE/dx, in Eq. (2.1), indicates that the energy is lost by the

particle. For a heavy particle, the collision energy-loss, dE/dx, is also referred to as

the stopping power.

In Sect. 1.3.1, we have derived the expression of the maximum energy trans-

fer W

for the relativistic scattering of a massive particle onto an electron at

rest. Usually, because the maximum energy transfer is much larger than the elec-

tron binding energy, this latter can be neglected. Thus, the value of W

is given

by formula (1.28), or, in most practical cases, by its approximate expression given

in Eq. (1.29): we will make use of this latter equation in the present chapter. Once

the approximate expression of W

is used, Eq. (2.1) (i.e., the energy-loss formula)

can be rewritten in an equivalent way as

−

4πnz

2mv

− β

−

, (2.2)

−

4πnz

L, (2.3)

where L is a dimensionless parameter called the stopping number, which contains

the essential physics of the process. In Eq. (2.3), L is given by the term in brackets

in Eq. (2.2). As discussed later, the stopping number can be modiﬁed by adding

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

34 Principles of Radiation Interaction in Matter and Detection

Fig. 2.2 Incoming fast particle of charge ze scattered by an atomic electron almost at rest: for

small energy transfer, the particle trajectory is not deﬂected.

correction terms which also depend on the particle velocity v, charge number z,

atomic target number Z and excitation energy I. Equation (2.1) and its equivalent

expression given by Eq. (2.2) are also termed Bethe–Bloch formula. In literature, the

Bethe–Bloch formula may also be found without the shell correction term. In this

latter form, it describes the energy-loss of a charged massive particle like a proton

with kinetic energy larger than a few MeV (e.g., see Sect. 2.1.1.2 and Section 27.2.1

of [PDB (2008)]).

Let us discuss an approximate derivation, i.e., without entering into complex

calculations, of the energy-loss formula following closely previous approaches [Fermi

(1950); Sternheimer (1961); Fernow (1986)]. In this way, the physical meaning of

the terms appearing in the formula and their behavior as a function of incoming

velocity become more evident. We restrict ourselves to cases where only a small

fraction of the incoming kinetic energy is transferred to atomic electrons, so that

the incoming particle trajectory is not deviated.

Now, we introduce the impact parameter b describing how close the collision

is (see Fig. 2.1): b is the minimal distance of the incoming particle to the target

electron. In general, large values of b correspond to the so-called distant collisions,

conversely small values to close collisions. Both kinds of collisions are important

for determining the average energy-loss [Eq. (2.1)], the energy straggling (i.e., the

energy-loss distribution) and the most probable energy-loss.

When a particle of charge ze interacts with an electron almost at rest

‡‡

, we as-

sume that, to a ﬁrst approximation, the electron will emerge only after the particle

passage so that we can consider the electron essentially at rest throughout the inte-

raction. This way, for symmetry reason (see Fig. 2.2), the transferred momentum

⊥

will be almost along the direction perpendicular to the particle trajectory. In

addition, the order of magnitude of the maximum strength of the Coulomb force act-

ing along the perpendicular direction F

⊥

is ≈ ze

. Thus, the maximum electric

‡‡

An electron is almost at rest, when its velocity is much smaller than the incoming particle

velocity v.

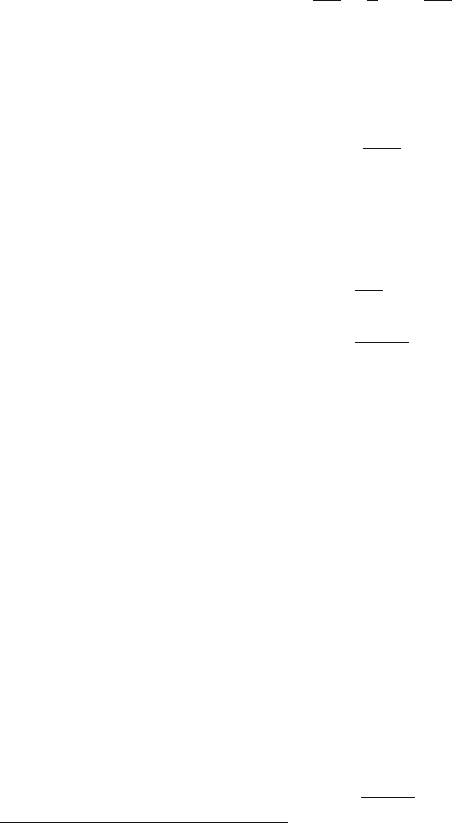
January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 35

ﬁeld strength, at which the Coulomb ﬁeld aﬀects the target electron, decreases as

the impact parameter increases. Furthermore, the interaction time between the two

particles is inversely proportional to the incoming particle velocity, v, and directly

proportional to b, namely the interaction time is ≈ b/v. Therefore, the transferred

momentum I

⊥

is given by:

⊥

∼

This estimate diﬀers by a factor 2 from a more reﬁned calculation (see for in-

stance [Fernow (1986)]), in which relativistic corrections are also considered while

estimating the perpendicular electric ﬁeld. Thus, we can ﬁnally write:

⊥

2ze

. (2.4)

Since the electron before the interaction was supposed to be at rest, its recoil mo-

mentum is I

⊥

. Its kinetic energy W , which is usually so small that we do not need

to deal with a relativistic formula, is given by:

W =

⊥

(2.5)

. (2.6)

Equation (2.6) shows the relationship between the impact parameter b and the

transferred energy W : distant collisions are typically soft ones, while close collisions

allow large transfers of kinetic energy, which goes as 1/b

. As a consequence, for

suﬃciently large b values the shell binding energies of electrons have to be taken

into account. Close collisions may happen with very large energy transfers, i.e., with

the emission of fast outgoing δ-rays. From Eq. (1.26), we see that, as the kinetic

energy of the δ-ray increases, the emission angle (the one formed with the incoming

particle direction) decreases: very fast δ-rays are emitted close to the particle tra-

jectory. Finally, we have to consider that the energy loss will ﬂuctuate from one

collision to the next, depending on collision distances.

Furthermore, the energy transferred to recoiling nuclei can be usually neglected

∗

with respect to the energy of recoiling electrons: their ratio is, typically, of the order

of a few 10

−4

. For any given value of b the kinetic energy (W ) acquired by a recoiling

electron is expressed by Eq. (2.6); while, if the interaction occurs on a nucleus with

charge Ze and mass m

, we have to rewrite Eq. (2.4) as:

A⊥

2Zze

. (2.7)

∗

For heavy ions with velocity of the order of (or lower than) the Bohr orbital velocity of electrons

in the hydrogen atom (deﬁned at page 74), the nuclear stopping power cannot be neglected (see

discussion in Sects. 2.1.4 and 2.1.4.1).

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

36 Principles of Radiation Interaction in Matter and Detection

Using Eq. (2.7), we can re-express Eq. (2.5) for estimating the recoil nuclear energy

as:

The ratio between the two recoil energies is

¶Áµ

When a particle interacts with an atom, the impact parameter is almost the same

for the Z atomic electrons and the nucleus. The overall transferred energy (W

) to

the electrons of the medium is about ZW and we have

On hydrogen (Z = 1), this ratio is ' 5.44 × 10

−4

, for heavier nuclei like Pb and

U it becomes ' 2.17 × 10

−4

and 2.12 × 10

−4

, respectively. It has to be noted that

the accumulated energy deposited in processes resulting from interactions on nuclei

is the dominant mechanism for (permanent) radiation damage by displacement in

Coulomb scatterings (e.g., see Chapter 4 and, for silicon devices, Chapter 6 and 7);

although, usually, it is negligible with respect to the overall energy lost by collisions

in traversing a medium (e.g., see Sects. 4.2.3 and 4.2.3.1).

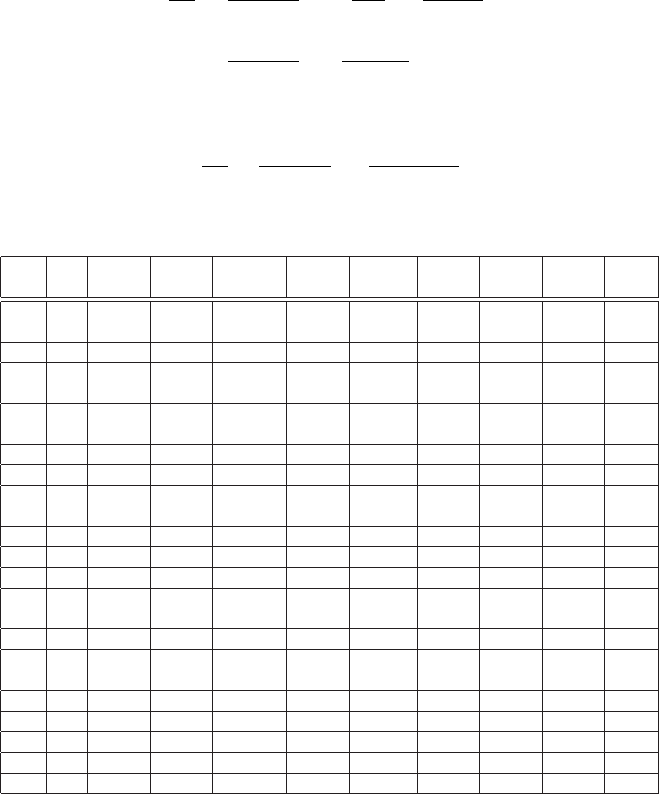
Let us consider (see Fig. 2.3) a particle of charge ze traversing a material, in

which the number of electrons per cm

is n [Eq. (1.40)]. The number of electrons

encountered by the particle along a path dx at impact parameter between b and

Fig. 2.3 An incoming fast particle of charge ze interacts with electrons at impact parameter

between b and b + db.

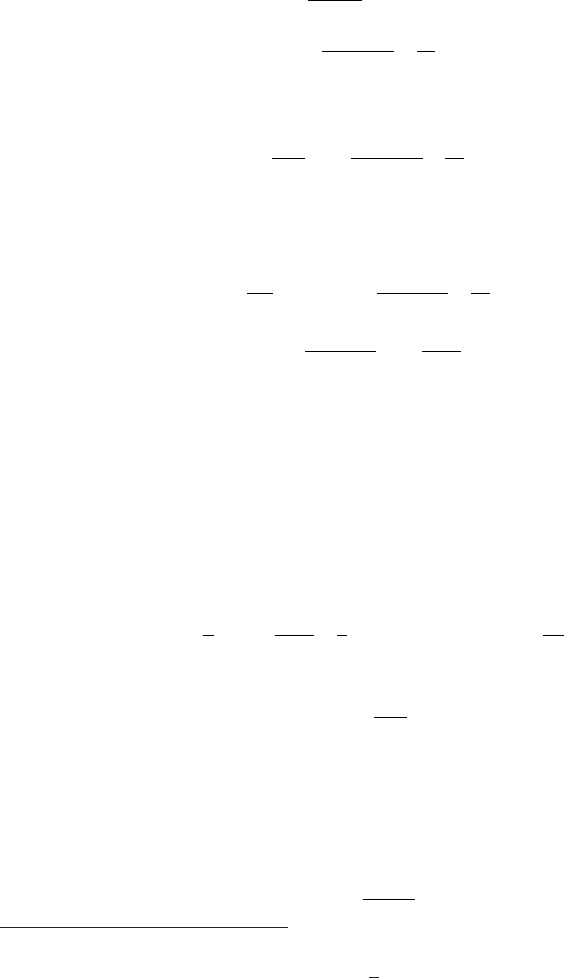
January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 37

b+db is n(2πb) db dx. From Eq. (2.6), the overall kinetic energy transferred to atomic

electrons is

n(2πb) db dx

4πnz

dx.

Thus, for impact parameters between b and b + db, the energy lost in a length dx

becomes:

−

4πnz

and the overall energy loss by collisions calculated by integrating from b

min

up to

max

, i.e., over the range of the impact parameter for which this approach is valid,

becomes

−

max

min

4πnz

max

min

. (2.8)

The upper limit b

max

can be estimated by considering that the collision time

τ cannot exceed the typical time period associated with bound electrons, namely

τ ' (1/¯ν) where ¯ν is the characteristic mean frequency of excitation of electrons. In

fact, if the collision time were much larger than the typical revolution period, the

passage of the particle could be considered as similar to an adiabatic process which

does not aﬀect the electron energy. In addition, at relativistic energies the region of

space at the maximum electric ﬁeld strength is contracted by the Lorentz factor γ

and, consequently, the collision time becomes ' b

max

/ (γv). Thus, for b

max

we have:

τ '

¯ν

max

and b

max

vγ

¯ν

Introducing the mean excitation energy I = h¯ν, we obtain:

max

vγh

. (2.9)

The lower limit b

min

is evaluated considering the extent to which the classical

treatment can be employed. In the framework of the classical approach, the wave

characteristics of particles are neglected. This assumption is valid as long as the

impact parameter is larger than the de Broglie wavelength

∗∗

of the electron in the

center-of-mass system (CoMS) of the interaction. For instance, we can assume

min

ecm

, (2.10)

∗∗

The de Broglie wavelength of a particle with momentum p is

λ =

where h is the Planck constant.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

38 Principles of Radiation Interaction in Matter and Detection

where P

ecm

is the electron momentum in the CoMS. Because the electron mass is

much smaller than the mass of the incoming heavy-particle, the CoMS is approx-

imately associated with the incoming particle and conversely the electron velocity

in the CoMS is opposite and almost equal in absolute value to that of the incoming

particle, v. Thus, we have that

ecm

| ' mγv = mγβc

and Eq. (2.10) becomes

min

' h/(2mγβc). (2.11)

Substituting the values of b

min

and b

max

in Eq. (2.8), we obtain:

−

4πnz

·µ

vγh

¶µ

2mγβc

¶¸

2πnz

2mγ

Finally, using the value of the maximum energy transfer W

from Eq. (1.29), we

get:

−

2πnz

2mv

(1 − β

)

. (2.12)

Table 2.1 Values of Z, Z/A, I, ρ, hν

and density-eﬀect parameters S

, S

, a, md, and

for some elemental substances.

El. Z Z/A I ρ hν

a md δ

eV g/cm

He 2 0.500 41.8 1.66 0.26 2.202 3.612 0.134 5.835 0.00

×10

−4

Li 3 0.432 40.0 0.53 13.84 0.130 1.640 0.951 2.500 0.14

O 8 0.500 95.0 1.33 0.74 1.754 4.321 0.118 3.291 0.00

×10

−3

Ne 10 0.496 137.0 8.36 0.59 2.074 4.642 0.081 3.577 0.00

×10

−4

Al 13 0.482 166.0 2.70 32.86 0.171 3.013 0.080 3.635 0.12

Si 14 0.498 173.0 2.33 31.06 0.201 2.872 0.149 3.255 0.14

Ar 18 0.451 188.0 1.66 0.79 1.764 4.486 0.197 2.962 0.00

×10

−3

Fe 26 0.466 286.0 7.87 55.17 -0.001 3.153 0.147 2.963 0.12

Cu 29 0.456 322.0 8.96 58.27 -0.025 3.279 0.143 2.904 0.08

Ge 32 0.441 350.0 5.32 44.14 0.338 3.610 0.072 3.331 0.14

Kr 36 0.430 352.0 3.48 1.11 1.716 5.075 0.074 3.405 0.00

×10

−3

Ag 47 0.436 470.0 10.50 61.64 0.066 3.107 0.246 2.690 0.14

Xe 54 0.411 482.0 5.49 1.37 1.563 4.737 0.233 2.741 0.0

×10

−3

Ta 73 0.403 718.0 16.65 74.69 0.212 3.481 0.178 2.762 0.14

W 74 0.403 727.0 19.30 80.32 0.217 3.496 0.155 2.845 0.14

Au 79 0.401 790.0 19.32 80.22 0.202 3.698 0.098 3.110 0.14

Pb 82 0.396 823.0 11.35 61.07 0.378 3.807 0.094 3.161 0.14

U 92 0.387 890.0 18.95 77.99 0.226 3.372 0.197 2.817 0.14

Data are from [Sternheimer, Berger and Seltzer (1984)]

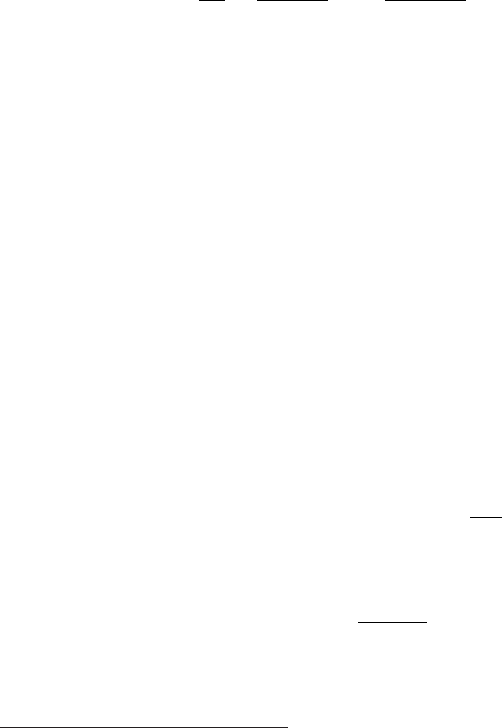
January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 39

This equation is equivalent to the energy-loss formula [see Eq. (2.1)] except for the

terms −2β

, −δ due to the density-eﬀect and the shell correction term (−U ). When

the ﬁrst of these latter terms is added to Eq. (2.12), using Eq. (1.29) we obtain the

expression (termed Bethe relativistic formula)

−

4πnz

2mv

I(1 − β

)

− β

(2.13)

derived in the quantum treatment of energy loss by collisions of a heavy, spin 0

incident particle [e.g., see the discussion in [Ahlen (1980)] and references therein;

see also [Fano (1963)]]. Furthermore, it has to be noted that spin plays an important

role when the transferred energy is almost equal to the incoming energy (this occurs

with very limited statistical probability). The other terms (−U and −δ) to be added

to Eq. (2.13) are discussed in Sects. 2.1.1.2 and 2.1.1.3, respectively. At low particle

velocity

††

, additional corrections are added: for instance, corrections accounting for

the Barkas eﬀect

‡‡

discussed in Sect. 2.1.1.1 and the Bloch correction

∗∗

discussed

later.

The Bloch correction (e.g., see [Northcliﬀe (1963)], Section D of [Ahlen (1980)],

[de Ferraiis and Arista (1984); Lindhard and Sørensen (1996)], Section 3.3.3

of [ICRUM (2005)] and Chapter 6 of [Sigmund (2006)]) derives from the Bloch

quantum-mechanical approach in which he did not assume, unlike Bethe, that it

is valid to consider the electrons

∗

to be represented by plane waves in the center-

of-momentum reference frame. It results in adding the quantity (e.g., see Equa-

tion 6.4 at page 184 of [Sigmund (2006)], [Northcliﬀe (1963)], Section D of [Ahlen

(1980)], Section 2.2 of [ICRUM (1993a)], Section 3.3.3 of [ICRUM (2005)] and re-

ferences therein)

∆L

Bloch

= Ψ(1) − Re

1 + j

z v

´i

(2.14)

to the stopping number [see Eq. (2.3)] of the energy-loss expression; in Eq. (2.14)

is the Bohr velocity (deﬁned at page 74, see also Appendix A.2), the function

Ψ(ι) =

d ln Γ(ι)

d ι

(called digamma function) is the logarithmic derivative of the gamma function and

Re denotes the real part. An accurate approximation for Eq. (2.14) can be obtained

from [de Ferraiis and Arista (1984)] (an approximated expression

†

can also be found

††

At very low velocity, the energy-loss process due to Coulomb interactions on nuclei (termed

nuclear energy-loss and resulting in the nuclear stopping power) cannot be neglected (e.g., see

Sects. 2.1.4, 2.1.4.1 and 2.1.4.1).

‡‡

For the Barkas eﬀect, the reader can see [Barkas, Dyer and Heckman (1963); Ashley, Ritchie and

Brandt (1972); Lindhard (1976); Bichsel (1990); Arista and Lifschitz (1999)]. This eﬀect is also

referred to as Barkas–Andersen eﬀect after the systematic investigations carried out by Andersen,

Simonsen and Sørensen (1969) (e.g., see Section 2.3.4 of [ICRUM (2005)]).

∗∗

It is determined by the diﬀerence between the Bloch non-relativistic expression and that one of

Bethe, see Section III of [Ahlen (1980)].

∗

The Bloch correction originates in close collisions (e.g., see Section 3.3.3 of [ICRUM (2005)]).

†

In Section 2.2 of [ICRUM (1993a)], the Block correction is approximated by the expression

−y

[1.20206 −y

(1.042 −0.8549 y

+ 0.343 y

)], where y = zα/β.