Leroy C., Rancoita P.-G. Principles Of Radiation Interaction In Matter And Detection

Подождите немного. Документ загружается.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

40 Principles of Radiation Interaction in Matter and Detection

in Section 37 of [Heitler (1954)], in [Bloch (1933); Bichsel (1990)] and in Section 2.2

of [ICRUM (1993a)]). The Bloch approach is meaningful for charged particles with

velocities

z v

zα

(e.g., see [Sigmund (1997, 1998)] and references therein), where the quantity 2z v

is referred to as the Bohr k parameter of a particle with charge ze and velocity

v. However, the correction can be neglected at large velocities (e.g., see [Northcliﬀe

(1963)] and Section 3.3.3 of [ICRUM (2005)]).

The energy-loss formula, as re-expressed in Eq. (2.2), shows that the logarith-

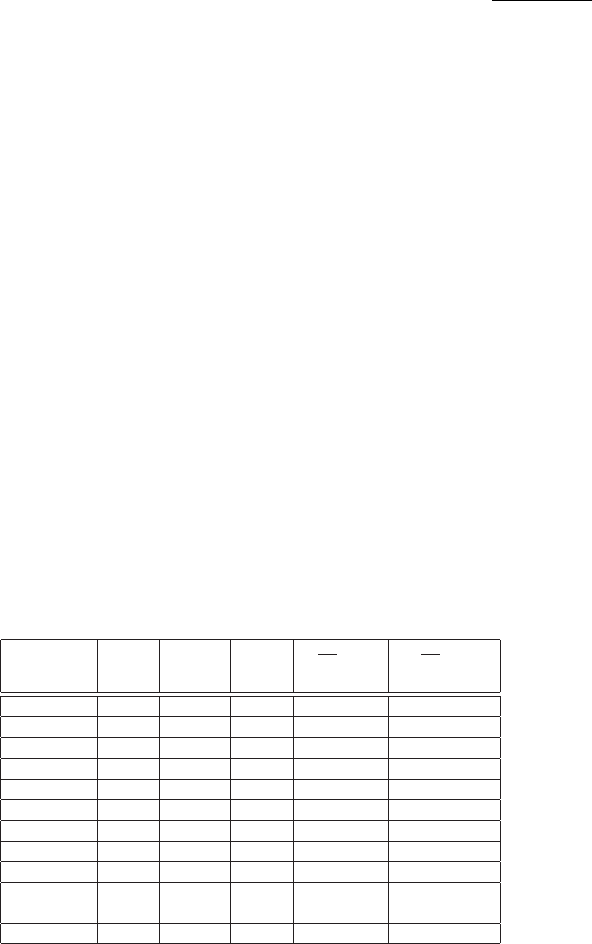
Table 2.2 Values of Z/A, I, ρ, hν

and density-eﬀect parameters S

, S

, a, and md for

some compounds and mixtures.

Material Z/A I ρ hν

a md

eV g/cm

(dry) Air 0.499 85.7 1.21 0.71 1.742 4.276 0.109 3.399

at sea level ×10

−3

Anthracene 0.527 69.5 1.28 23.70 0.115 2.521 0.147 3.283

Ethane 0.599 45.4 1.25 0.79 1.511 3.874 0.096 3.610

×10

−3

Ethyl Alcohol 0.564 62.9 0.79 19.23 0.222 2.705 0.099 3.483

Freon-12 0.480 143.0 1.12 21.12 0.304 3.266 0.080 3.463

(lead) Glass 0.421 526.4 6.22 46.63 0.061 3.815 0.095 3.074

Kapton,

polyimide ﬁlm 0.513 79.6 1.42 24.59 0.151 2.563 0.160 3.192

Lithium

carbonate 0.487 87.9 2.11 29.22 0.055 2.660 0.099 3.542

Methane 0.623 41.7 6.67 0.59 1.626 3.972 0.093 3.626

×10

−4

Methanol 0.562 67.6 0.79 19.21 0.253 2.764 0.090 3.548

Plastic scint.,

vinyltoluene 0.541 64.7 1.03 21.54 0.146 2.486 0.161 3.239

Polyethylene 0.570 57.4 0.94 21.10 0.137 2.518 0.121 3.429

Propane 0.590 47.1 1.88 0.96 1.433 3.800 0.099 3.592

×10

−3

Lucite 0.539 74.0 1.19 23.09 0.182 2.668 0.114 3.384

Silicon

dioxide 0.499 139.2 2.32 31.01 0.139 3.003 0.084 3.506

Tissue,

soft (ICRP) 0.551 72.3 1.00 21.39 0.221 2.780 0.089 3.511

Tissue,

soft (ICRP

four-comp.) 0.550 74.9 1.00 21.37 0.238 2.791 0.096 3.437

Tissue-equiv., 0.550 61.2 1.06 0.70 1.644 4.140 0.099 3.471

gas (methane

base) ×10

−3

Tissue-equiv., 0.550 59.5 1.83 0.91 1.514 3.992 0.098 3.516

gas (propane

base) ×10

−3

Data are from [Sternheimer, Berger and Seltzer (1984)]

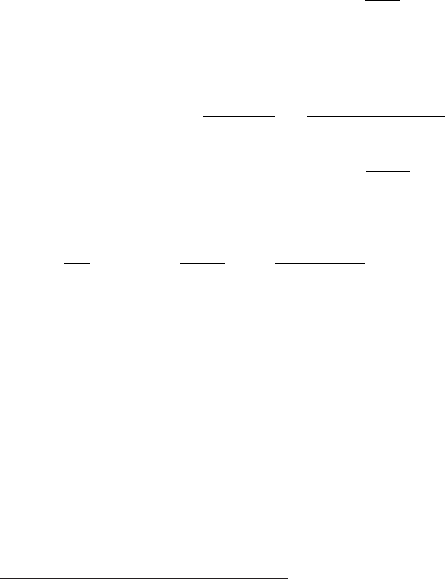
January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 41

mic term increases quadratically with βγ = (vγ)/c. The reason for such a behavior

[see Eq. (2.8)] is that the energy loss depends on ln (b

max

min

). Both terms 1/b

min

[Eq. (2.11)] and b

max

[Eq. (2.9)] increase with βγ. The former refers to the en-

hancement of the maximum transferable kinetic energy (which goes as 1/b

) in a

single collision, while the latter refers to the Lorentz dilatation of the maximum

impact parameter (conversely, the transverse volume aﬀected by the incoming elec-

tric ﬁeld). Therefore, as the incoming particle energy increases, δ-rays are emitted

more energetically along the particle trajectory (see also Sect. 2.1.2). In addition

the cylindrical region, surrounding the particle path and experiencing excitation

and ionization, is enlarged.

The phenomenon of δ-ray emission is mostly responsible for the diﬀerence bet-

ween the energy lost by a particle traversing a medium (for example, the thin ab-

sorbers used in Si or gaseous detectors) and the energy actually deposited inside. As

a consequence, although the energy lost continues to increase with increasing energy

[Eq. (2.2)], the deposited energy approaches an almost constant value [termed Fermi

Plateau

∗

, see also Eq. (2.29)], which mainly depends on the size and density of the

absorber (see discussion in Sect. 2.1.1.4).

By introducing the classical electron radius,

(2.15)

(see Appendix A.2) and using Eq. (1.40), we can evaluate the numerical coeﬃcient

in Eq. (2.1):

2πnz

2πNmc

ρz

A β

= 0.1535

ρz

A β

[MeV/cm], (2.16)

and, thus, the energy-loss formula becomes

−

= 0.1535

ρz

Aβ

2mv

(1 − β

)

− 2β

− δ − U

[MeV/cm], (2.17)

where, to a ﬁrst approximation, the value of the mean excitation energy is given

by [Marmier and Sheldon (1969)]:

I ≈ 11.5 × Z × 10

−6

[MeV]

I ≈ 9.1 × Z(1 + 1.9 × Z

−2/3

) 10

−6

[MeV].

Values of Z/A, ρ and I for several elemental substances, compounds and mixtures

are available in literature (e.g., see [Sternheimer, Berger and Seltzer (1984)]; see,

also, [Ahlen (1980); Bichsel (1992); ICRUM (1993a, 2005)]) and on the web [NIST

(2008)]; some of them are listed in Tables 2.1 and 2.2.

∗

The Fermi Plateau is discussed in Sect. 2.1.1.4.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

42 Principles of Radiation Interaction in Matter and Detection

2.1.1.1 The Barkas–Andersen Eﬀect

The Barkas eﬀect

∗

denotes the observed diﬀerence in ranges of positive and neg-

ative particles in emulsion. Barkas and collaborators provided the ﬁrst indication

that π

−

-ranges were slightly longer than π

-ranges [Smith, Birnbaum and Barkas

(1953)]. Subsequently, Barkas, Dyer and Heckman (1963) obtained a precise result

by investigating the process

−

+ p → Σ

+ π

∓

For this reaction, range measurements in emulsion

†

allowed them i) to deter-

mine that the rest masses

‡

of Σ

and Σ

−

hyperons were 1189.35 ± 0.15 MeV and

1197.6 ± 0.5 MeV, respectively and ii) to observe the energy-loss defect of negative

hyperons [i.e., a range larger than expected by about (3.6 ±0.7)%]. The energy-loss

defect was interpreted as the experimental evidence that a stopping-power theory

based on the Born approximation (e.g., see footnote at page 17) must be corrected

when the particle velocity b ecomes comparable to that of atomic electrons in stop-

ping materials [Barkas, Dyer and Heckman (1963); Fano (1963)]. In fact, the next-

high-order correction to Born approximation contributes to the stopping power in

proportion to the cube of the incident particle’s charge (ze)

[Fano (1963)]. Thus,

it results to be of opposite sign for negative and positive particle pairs.

Furthermore, Andersen, Simonsen and Sørensen (1969) carried out high-

precision measurements of the stopping powers of aluminum and tantalum for (5–

13.5) MeV p and d, and (8–20) MeV

He and

He. They determined that the ratio

between the stopping powers for the doubly charged and singly charged ions is sys-

tematically larger than the factor four predicted by the energy-loss formula. The

computed charge-dependent correction to Eq. (2.2) was in agreement to that needed

for the range diﬀerence between Σ

and Σ

−

hyperons measured by Barkas, Dyer

and Heckman (1963). This eﬀect may better be referred to as the Barkas–Andersen

eﬀect (see also [ICRUM (2005)]).

For suﬃciently slow incoming particles, the collision time becomes long enough

for allowing atomic electrons to considerably move during the interaction. When this

occurs, the exp erimental data suggest that i) it results in a smaller eﬀective impact

parameter for positively charged particles, thus in an increase of the transferred

energy and ii) the reverse occurs for negatively charged particles. Ashley, Ritchie

and Brandt (1972) proposed the ﬁrst theoretical treatment of the Barkas–Andersen

eﬀect. Their approach was within the framework of Bohr’s oscillator model [Bohr

(1913)]. However, it was limited to distant collisions, under the assumption that

close collisions make a negligible contribution: it showed that the Barkas correc-

∗

It was termed in this way by Lindarhd (1976).

†

Properties of photographic emulsions are discussed in [Blau (1961)].

‡

These values are well in agreement, within experimental errors, with those reported in [PDB

(2008)].

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 43

Fig. 2.4 Stopping numbers, ratio and diﬀerence of the stopping numbers for positive (L

) and

negative (L

−

) incident particles with charge |Z

|e as a function of ζ

[Eq. (2.20)] (reprinted

from Nucl. Instr. and Meth. in Phys. Res. B 212, Sigmund, P. and Schinner, A., Anatomy of

the Barkas eﬀect, 110–117, Copyright (2003), with permission from Elsevier). The Bohr logarithm

[= ln(C ζ

) with C = 1.1229] is also included for comparison.

tion

‡‡

is governed by the parameter (entering Bohr’s energy-loss formula)

ζ =

, (2.18)

where m and e are the electron rest mass and charge, respectively; ω is the cir-

cular velocity of the (isotropically) bound electrons

††

; v and z are the incoming

particle velocity and charge number, respectively. Lindhard (1976) determined that

close collisions make a signiﬁcant contribution almost doubling the estimate for the

Barkas correction. Equation (2.18) indicates that this latter is relevant i) at small

v, ii) large charge number z and iii) large ω, i.e., for inner shells. According to

Andersen (1983, 1985) and Bichsel (1990), experimental data

†

are consistent with

Barkas corrections

∗∗

estimated by [Lindhard (1976)]. For target elements with high

atomic number, Bichsel (1990) extracted the correction to be added to the stopping

numb er from measured stopping powers and found that an accurate expression is

‡‡

As for the Bloch correction, the Barkas correction is added to the stopping number [see

Eq. (2.3)].

††

For atoms with mean excitation energy I, this dominant resonance value ω is given by ω = I/~.

†

These data were based on the determination of the stopping powers for protons, α-particles and

lithium ions.

∗∗

Lindhard’s results are considered consistent with experimental data at least for target atomic

numbers Z < 50 (e.g., see Section 2.3 of [ICRUM (1993a)]).

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

44 Principles of Radiation Interaction in Matter and Detection

obtained by the empirical formula

∆L

Barkas

= z g

−2 g

. (2.19)

For gold (and for elements with Z ≥ 64 [ICRUM (1993a)]), we have g

= 0.002833

and g

= 0.60; for silver (Z = 47), g

= 0.006812 and g

= 0.45, while for aluminum

(Z = 13), g

= 0.001054 and g

= 0.80.

Sigmund and Schinner (2001a) showed that the Barkas–Andersen eﬀect is well

predicted for the antiproton stopping power in silicon and, in general, is well under-

stoo d in case of light ions. Furthermore, Sigmund and Schinner (2003) investigated

the scaling properties of the eﬀect and found that i) the ratio of the stopping num-

bers for an ion and its anti-ion is almost independent of the charge number z,

increases almost monotonically with decreasing

|ζ|

|z|e

(2.20)

and has a local maximum at ζ

= 0.26 (Fig. 2.4), i.e., at constant ion speed the

relative magnitude of the Barkas eﬀect increases with increasing z, ii) the ratio has

a more complex dependence on Z and iii) the diﬀerence of these stopping numbers

has a maximum at ζ

= 3.3 and becomes negligible for ζ

& 100 (Fig. 2.4).

Furthermore, Sigmund (1998) (see also [Sigmund (1997)]) indicates that the

ratio of Bloch to Barkas corrections is given by

Bloch correction

Barkas correction

∼

z v

Z v

where v

is the Bohr velocity.

2.1.1.2 The Shell Correction Term

Following the Pauli exclusion principle (see for instance textbooks like [Finkelnburg

(1964); Eisberg and Resnick (1985)]), the only permitted arrangements of electrons

in atoms or molecules are those in which at least one of the four quantum numbers

(principal, azimuthal,

magnetic and spin) diﬀers. The principal quantum number

indicates the shell number. Starting from the inner one, we have 1, 2, 3, 4, . . . These

shells are indicated with the letters K, L, M, N, . . . The orbital quantum numbers

(0, 1, 2, 3, . . .) are indicated with the letters s, p, d, f, . . . (see Appendix A.4 on the

Electronic Structure of the Elements).

For an absorber with atomic number Z, the shell correction term

U = 2

in Eq. (2.1) is due to the non-participation of inner (K, L, . . .) electrons in the

collision loss process (see for instance [Walske (1962); Fano (1963); Marmier and

Sheldon (1969); Lindhard (1976); Ahlen (1980)] and references therein), when the

It is also called the orbital angular momentum quantum number.

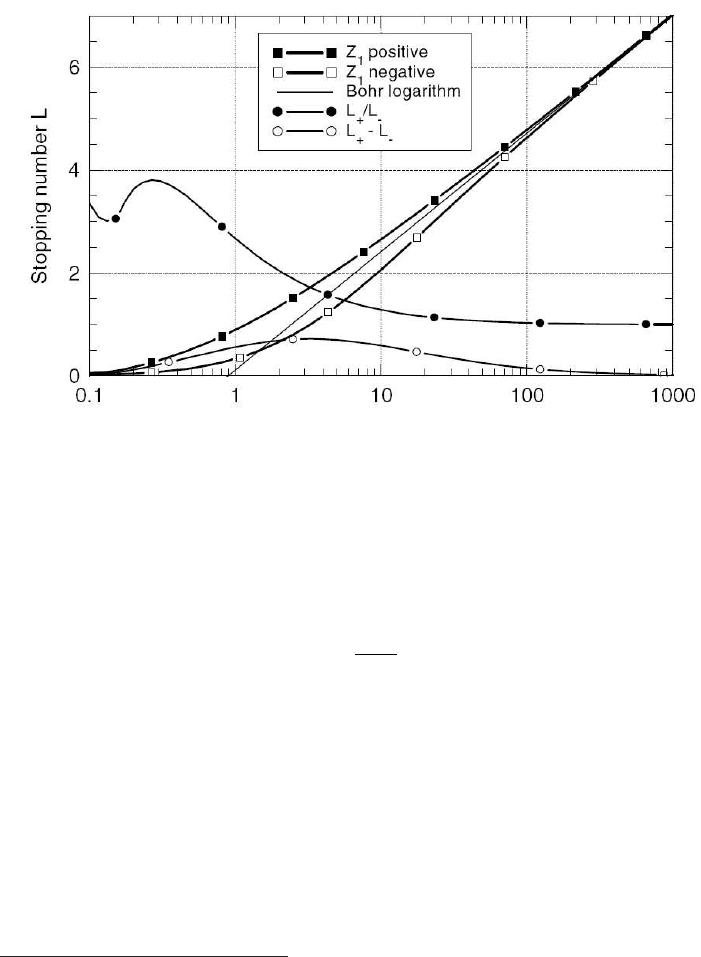
January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 45

Fig. 2.5

versus incoming proton kinetic energy in Ne, Ar, Kr and Xe absorbers (adapted

and reprinted with permission from [Andersen (1983)]), see text at page 45.

incoming velocity is no longer much larger than that of bound atomic electrons. De-

tailed calculations of K and L shells were carried out [Walske (1962); Fano (1963);

Lindhard (1976)]. The corrections for the M, N, and higher shells of heavy atoms

are generally small, except at very low energies (namely for proton kinetic energies

≤ 1 MeV).

The estimated values [Fano (1963)] of

for protons traversing metals are

lower than 0.1 when β > 0.05

√

The

values were experimentally determined for protons traversing noble

gases and are shown in Fig. 2.5 (see [Andersen (1983)] for explanation on theoretical

predictions): the shell correction term cannot be neglected for proton energies lower

than a few MeV’s. Further treatments and references on this correction term can

be found in [ICRUM (1993a)] for protons and α-particles, and in [ICRUM (2005)]

for ions heavier than helium. Sigmund (1998) (see also [Sigmund (1997)]) indicates

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

46 Principles of Radiation Interaction in Matter and Detection

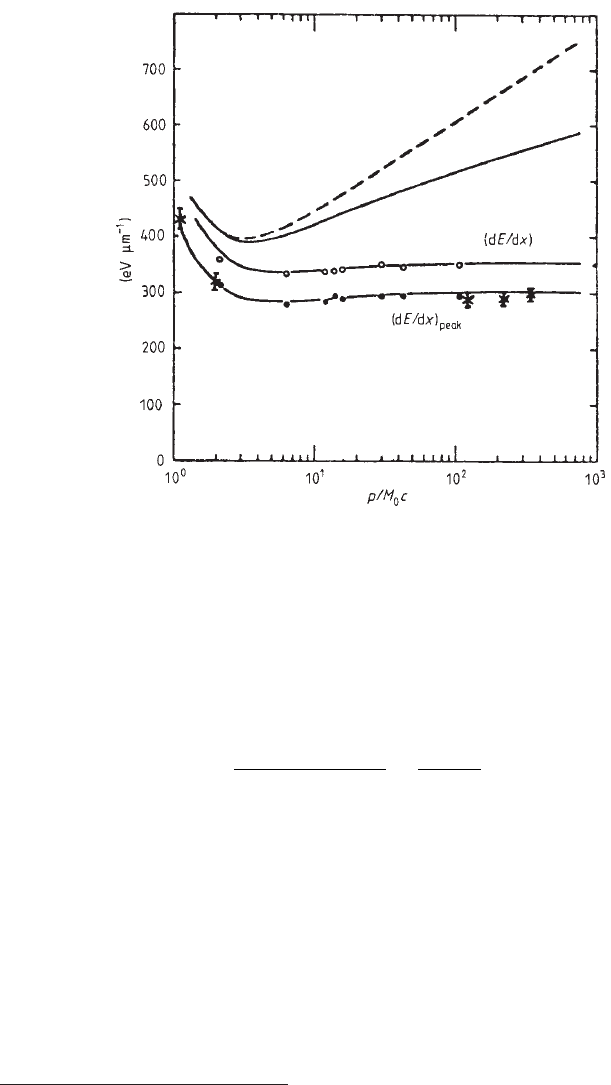
Fig. 2.6 Energy loss in silicon (in units of eV/µm) versus βγ (= p/M

c, where M

is the rest mass

of the incoming particle) from [Rancoita (1984)]. From the top the ﬁrst two curves are: −dE/dx

without (broken curve) and with (full curve) the density-eﬀect correction. The following two other

curves are compared to experimental data for detector thicknesses of 300 (× from [Hancock, James,

Movchet, Rancoita and Van Rossum (1983)]) and 900 µm (◦ and • from [Esbensen et al. (1978)]):

the restricted energy-loss with the density-eﬀect taken into account and the prediction of the most

probable energy-loss.

that the ratio of Barkas to shell corrections is given by

Barkas correction

shell correction

∼

z v

2 Z

1/3

where v

is the Bohr velocity; v and z are the incoming particle velocity and charge

numb er, respectively.

A detailed discussion on stopping power, energy straggling and total range for

ions with energies

lower than 10 MeV/nucleon is given in [Ziegler, Biersack and

Littmark (1985a); Ziegler, J.F. and M.D. and Biersack (2008a)]. However, this goes

beyond the ﬁeld of interest of this book.

2.1.1.3 The Density Eﬀect and Relativistic Rise

The energy-loss formula [Eq. (2.1)] shows that, at low β values, the collision energy-

loss (−dE/dx) decreases rapidly as the velocity increases owing to the 1/β

term. At

The reader can ﬁnd the deﬁnition of kinetic energies per nucleon in Sect. 1.4.1.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 47

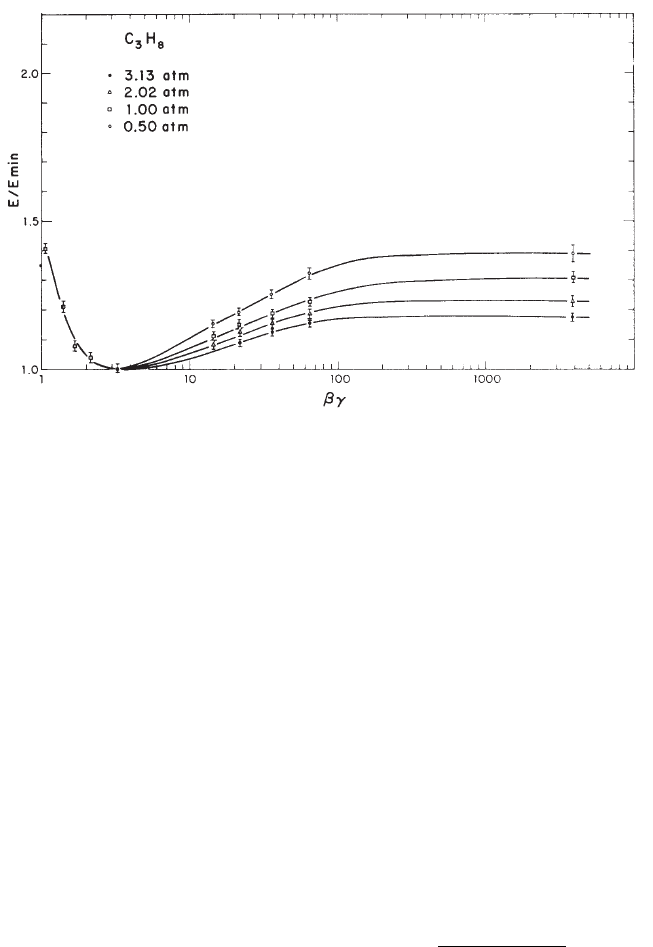
Fig. 2.7 Measured energy-loss (reprinted from Nucl. Instr. and Meth. 161, Walenta, A.H.,

Fisher, J., Okuno, H. and Wang, C.L., Measurement of the Ionization Loss in the Region of

Relativistic Rise for Noble and Molecular Gases, 45–58, Copyright (1979), with permission from

Elsevier) in propane normalized to the energy-loss minimum E

min

versus βγ. The diﬀerent slopes

of the relativistic rise eﬀect depend on the detecting device pressure.

relativistic energies, when the velocity approaches the speed of light and β ≈ 1, the

energy-loss curve reaches a minimum, called the energy-loss minimum, for

min

≈ 3 (2.21)

(corresponding to β

min

≈ 0.95). A particle at the energy-loss minimum is called a

minimum ionizing particle (mip).

The collision energy-loss will start to grow again beyond its minimum due to

the logarithmic term. This latter depends on the increase with the incoming mo-

mentum, of both the maximum transferred energy and b

max

. However, as the range

of the distant collision is extending, the atoms close to the path of the particle will

produce a polarization, which results in reducing the electric ﬁeld strength acting on

electrons at large distances, as pointed out by Fermi (1939) and others (for instance

see [Sternheimer (1961)]).

Bohr ([Ritson (1961)] and references therein) demonstrated that the screening

becomes more eﬀective at impact parameters of ≈

(mc

)/(4πne

). At distances

exceeding this value of the impact parameter, the electric shielding prevents the

energy transfer. Furthermore, in the region where the density-eﬀect correction needs

to be applied, the shell correction term is negligible.

Systematic studies of this eﬀect were carried out ([Sternheimer (1966); Stern-

heimer and Peierls (1971); Sternheimer, Berger and Seltzer (1984)]; Section 3.4

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

48 Principles of Radiation Interaction in Matter and Detection

in [Groom, Mokhov and Striganov (2001)] and references therein). The actual cor-

rection term, δ, due to the density-eﬀect can be obtained by the following set of

equations as function of the βγ value:

δ = δ

βγ

(for βγ < 10

), (2.22)

δ = 2 ln(βγ) + C + a

ln 10

βγ

¶¸

(for 10

< βγ < 10

) (2.23)

and, ﬁnally,

δ = 2 ln(βγ) + C (for βγ > 10

); (2.24)

where C is given by

C = −2 ln

hν

− 1

and

πm

(2.25)

is the plasma frequency. The parameters S

, S

, hν

, md and a are given in Ta-

bles 2.1 and 2.2. The values of δ

(see Table 2.1) are lower than 1, as well as the

term

βγ

. As a consequence, the correction for the density-eﬀect is small at low

energy. In fact, the term in brackets in Eq. (2.1) is not less than ≈ 16 for βγ ≈ 3

[namely for particles close to the energy-loss minimum, see Eq. (2.21)], even for

high-Z materials for which excitation energies are higher. At larger values of βγ

(where β is ≈ 1 and for βγ > 10

), the density-eﬀect correction approaches a

linear dependence on ln(βγ). The term in brackets in Eq. (2.1) becomes:

2mv

(1 − β

)

− 2 − 2 ln(βγ) − C = ln

2mβ

¶¸

− 2 − C

= ln

2mc

(hν

)

− 1.

The energy-loss formula can be ﬁnally rewritten as:

−

= 0.1535

ρz

2mc

(hν

)

− 1

[MeV/cm]. (2.26)

In Eq. (2.26), the logarithmic dependence of the energy lost by an incoming

massive particle is determined only by the maximum transferred energy W

in a

single collision: the energy-loss increasing beyond its minimum is called relativistic

rise. This increase [see Eq. (1.29)] depends on ln(β

), but in the ultra-relativistic

region it depends on ln γ [see Eq. (1.28)]. In Fig. 2.6 (see [Rancoita (1984)] and

references therein), the calculated energy-loss curve (shown by the broken curve,

for which the relativistic rise depends on W

and b

max

) and the one including

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 49

the density-eﬀect correction (shown by the full curve, for which the relativistic rise

depends on W

only) are presented for silicon detectors.

In Fig. 2.7 [Walenta, Fisher, Okuno and Wang (1979)], data on energy-loss are

presented as a function of the pressure of the detecting gas device. As the pressure in-

creases (i.e., n increases), the value of C, which depends on ln{I/[h

(ne

)/(πm)]},

decreases: at ﬁxed values of βγ, the density-eﬀect correction is larger [see at page

48 the expressions for the density-eﬀect correction, e.g., Eqs. (2.23, 2.24)].

2.1.1.4 Restricted Energy-Loss and Fermi Plateau

We have seen how the energy loss by collisions continues to rise with the increase

of the incoming particle energy. This occurs because the maximum energy transfer

in a single collision depends on the Lorentz factor γ (at ultra high energies), or

on γ

at relativistic energies (see Sect. 1.3.1). This kinetic energy is transferred to

electrons (δ-rays) emitted in directions close to the one of the incoming particle and,

being energetic, they can travel large distances inside the medium or escape from

it. Therefore, the energy transferred by the incoming particle to atomic electrons can

result in secondary ionization processes, similar to the primary one, with additional

δ-rays traveling far away from the emission point.

Typical radiation or particle detectors are not thick enough to absorb secondary

δ-rays fully. Thus, the energy loss suﬀered by the incoming particle diﬀers from

the deposited energy inside the detecting medium. Furthermore, we need to deﬁne

an eﬀective detectable maximum transferred energy W

. This maximum detectable

energy is the eﬀective average maximum δ-ray energy that can be absorbed inside

the device also taking into account the emission angles.

Table 2.3 Values of the radiation length (X

), critical energy (²

)

using Eq. (2.121), Moli`ere radius (R

) using Eq. (2.239) and stop-

ping power for a massive z = 1 particle for several materials.

Material X

mip

dχ

mip

cm MeV cm MeV/cm MeV cm

Be 35.28 111.47 6.71 2.947 1.595

Al 8.89 40.28 4.68 4.361 1.615

Si 9.36 37.60 5.28 3.877 1.664

Fe 1.76 21.04 1.77 11.419 1.451

Cu 1.44 18.96 1.60 12.571 1.403

W 0.35 8.08 0.92 22.099 1.145

Pb 0.56 7.42 1.60 12.735 1.122

U 0.32 6.77 1.00 20.485 1.081

Water 36.08 70.10 10.91 1.992 1.992

NEMA 19.40 52.38 7.85 3.179 1.870

G10 plate

BGO 1.12 10.20 2.33 8.882 1.251

See [Leroy and Rancoita (2000)], Section 6 in [PDB (2008)] and

Eq. (2.17).