Leroy C., Rancoita P.-G. Principles Of Radiation Interaction In Matter And Detection

Подождите немного. Документ загружается.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

50 Principles of Radiation Interaction in Matter and Detection

In order to estimate the deposited energy inside a detector, we have to rewrite

the energy-loss formula [Eq. (2.1)], in terms of W

. Following the treatment by

Fano (1963), the electromagnetic interaction for relativistic particles is approxi-

mated by the usual static Coulomb interaction (the longitudinal term) and with

a relativistic transverse term. The overall interaction is evaluated by considering

three diﬀerent regions of the transferred energy W

i) W < W

for which the momentum transfer is ¿ ~/a

, where a

is the linear

dimension of the target atom:

−

2πnz

2mv

(1 − β

)

− β

ii) W

< W < W

, where the transverse term can be neglected and W/(mc

)¿1:

−

2πnz

iii) W

< W < W

, namely W values large enough to consider the atomic

electrons of the target as free:

−

2πnz

− W

1 − β

2mc

¶¾

For absorbers thick enough so that the corresponding eﬀective detectable maximum

transferred energy (W

) satisﬁes the condition of the above-described point (ii) (i.e.,

< W

), we can rewrite the latter expression as:

−

2πnz

− W

1 − β

2mc

¶¾

Summing the three contributions and adding b oth the density-eﬀect and the shell

correction terms, we obtain the so-called restricted energy-loss formula valid for

≥ W

> W

−

restr

2πnz

2mv

(1 − β

)

−β

−W

1 − β

2mc

−δ− U

. (2.27)

It has to be noted that when W

→ W

for W

≈ 2mc

, then, Eq. (2.27)

reduces to Eq. (2.1).

The term

1 − β

2mc

can be neglected for incoming particle energies beyond the ionization loss minimum

or for W

¿ 2mc

. When these conditions are satisﬁed and using Eq. (2.16), for

≥ W

we obtain:

−

restr

= 0.1535

ρz

Aβ

2mv

(1 − β

)

− β

− δ − U

[MeV/cm]. (2.28)

At high energies (when β ≈ 1 and βγ > 10

), we can neglect the shell correction

term and express the density correction [Eq. (2.24)] as δ = 2 ln(γ) + C, where

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 51

Fig. 2.8 Stopping power (-dE/dx) in eV/µm of protons in silicon for 1.5×10

−3

. βγ ≤5 (data

from [Berger, Coursey, Zucker and Chang (2005)]). The contribution of the nuclear stopping power

is included: it decreases rapidly for βγ & 3 × 10

−3

; at βγ ∼ 3 × 10

−3

it does not exceed 3.4%.

C = −2 ln

hν

−1 (see page 48) and ν

(the plasma frequency) is computed using

Eq. (2.25). Because W

does not depend any more on the incoming particle energy,

the collision loss will reach a constant value, called the Fermi plateau, computed by

rewriting Eq. (2.28) for W

≥ W

as:

−

plateau

= 0.1535

ρz

2mv

(1 − β

)

− 1 − 2 ln(γ) − C

= 0.1535

ρz

2mc

(hν

)

[MeV/cm]. (2.29)

This equation replaces the formula (2.26) whenever the deposited energy has to

be computed instead of the energy-loss formula. In Eq. (2.29) the incoming energy

dependent term W

is substituted by the constant W

term. This term has to be

evaluated, in turn, for any given detector and detector thickness medium.

In Fig. 2.7 [Walenta, Fisher, Okuno and Wang (1979)], experimental data taken

with a gas detector show evidence of the Fermi plateau beyond βγ ≈ 130. From the

energy-loss minimum to the Fermi plateau, data exhibit the relativistic rise.

In Fig. 2.6, experimental data collected with silicon detectors show the Fermi

plateau, as well. The escaped δ-rays result in a lower measured energy-loss depo-

sition (i.e., deposited energy) with respect to the expected one, as derived by the

energy-loss formula expressed by Eq. (2.17). For instance at the energy-loss mini-

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

52 Principles of Radiation Interaction in Matter and Detection

mum [Eq. (2.21)] and for z = 1, from Eq. (2.17) and Table 2.1 the computed value

of −(dE/dx) in silicon is ≈ 3.87 MeV/cm or equivalently ≈ 387 eV/µm. For the

900 µm thick silicon detector of [Esbensen et al. (1978); Rancoita (1984)], the value

of W

is ≈ 0.5 MeV and the restricted energy-loss value calculated from Eq. (2.28)

is ≈ 345 eV/µm in agreement with the experimental data shown in Fig. 2.6. Fur-

thermore, the Fermi plateau computed by means of Eq. (2.29) is only ≈ 10 eV/ µm

higher than the restricted energy-loss at the minimum: in dense media like silicon,

the relativistic rise may become almost negligible. In silicon detectors, the active

layer thickness is typically (300–400) µm and, thus, it can absorb δ-rays with ki-

netic energies not exceeding ≈ 300 keV (e.g., see page 94). However, as mentioned

above, 900 µm thick absorbers were also used. For instance, from Eq. (1.29), the

maximum transferred kinetic energy is ≈ 0.3 (0.5) MeV for a proton with kinetic

energy of ≈ 128 (207) MeV, i.e. with βγ ≈ 0.54 (0.70). Therefore, the non-complete

absorption of emitted δ-rays aﬀects the energy-deposition curve in silicon detec-

tors for incoming protons (or other heavy charged particles) with βγ & 0.54–0.70

(e.g., see Fig. 2.6). In Fig. 2.8, the stopping power (-dE/dx) in eV/µm of protons

in silicon is shown for 1.5 ×10

−3

. βγ ≤ 5 (data from [Berger, Coursey, Zucker and

Chang (2005)]). Is included the nuclear stopping power, which decreases rapidly for

βγ & 3 × 10

−3

; at βγ ∼ 3 × 10

−3

it does not exceed 3.4% (see also Sect. 2.1.4.1).

For W

≥ W

, the diﬀerence, 4

−

, between the energy-loss formula

[Eq. (2.17)] and the restricted energy-loss equation [Eq. (2.28)] is given by:

−

= 0.1535

ρz

Aβ

− β

[MeV/cm]. (2.30)

2.1.1.5 Energy-Loss Formula for Compound Materials

Experimental stopping power measurements were mostly carried out on elements

rather than compounds. To a ﬁrst approximation, see for instance [Sternheimer

(1961); Fano (1963)], a material containing several atomic species can be treated

according to Bragg’s additivity rule, namely as a combination of atoms contribut-

ing to the overall stopping power, separately. The energy-loss formula is valid for

compounds and mixtures. But the mean excitation energy I, the ratio Z/A and the

density correction term δ appearing in Eq. (2.1) [or for instance in the equivalent

expression of Eq. (2.17)] have to b e replaced by

δ,



, which are given by:

I =

ln I

, (2.31)

δ =

, (2.32)

, (2.33)

This value is in agreement with the one given in Table 2.3, see also Section 6 in [PDB (2008)]

and Fig. 2.8.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 53

where n

is the number of atoms of ith species present in the stopping material, and

, A

, Z

are the mean excitation energy, the atomic weight and the atomic number

of that atomic element, respectively. The oscillator strength f

for the atoms of the

ith species is given by

≡

. (2.34)

This approach was shown to be usually accurate enough, even though it dis-

regards chemical binding and other materials prop erties [Fano (1963)]. Equa-

tions (2.31–2.33) can also be found expressed using fractions by weight (w

) of

compound or mixture elements

and, thus, with oscillator strengths re-expressed as

Á¿

. (2.35)

Values of Z/A, I and density-eﬀect parameters S

, S

, a, and md [see Eqs. (2.22–

2.24)] for several compounds and mixtures are available in literature (e.g., see [Stern-

heimer, Berger and Seltzer (1984)]): some of them are listed in Table 2.2.

At low energy, the application of the additivity rule can introduce errors, because

the stopping power contributed by each element is inﬂuenced by chemical binding

eﬀects. These errors can amount to ≈ 15% at energies near the stopping power

peak [ICRUM (1993a)]. In addition, the stopping powers also depend on the material

phase: they are generally lower for solids than for gases. A detailed discussion of

energy-loss in compounds and mixtures is beyond the purp ose of this book. The

reader can ﬁnd a literature survey on this subject in Section 3.2 of [ICRUM (1993a)]

(see also Section 3.5 of [ICRUM (2005)]).

In [Berger, Coursey, Zucker and Chang (2005)], the databases PSTAR (for pro-

tons) and ASTAR (for α-particles) provide the stopping-powers for protons and

α-particles in several compounds and mixtures up to 10 and 1 GeV, respectively.

2.1.2 Energy-Loss Fluctuations

The energy-loss process experienced by a charged particle in matter is a statistical

phenomenon: the collisions responsible for energy losses are (to a ﬁrst approxi-

mation) a series of independent successive events.

Each interaction of the incoming particle with atomic electrons can transfer

a diﬀerent amount of kinetic energy. Equation (2.1) allows one to compute the

average energy-loss, but this value undergoes statistical ﬂuctuations. Therefore, the

energy lost by a particle, in a given traversed path x, will be characterized by an

energy distribution function called the energy-loss distribution function or energy

straggling function. For electrons at high energy, the collision process is not the

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

54 Principles of Radiation Interaction in Matter and Detection

dominant interaction by which energy is released and, as consequence, is not the

main cause of energy-loss ﬂuctuations. On the contrary, this is the dominant process

for massive charged particles.

2.1.2.1 δ-Rays, Straggling Function, and Transport Equation

Let us consider the probability P (², E) that a particle of energy E traversing a

thickness dx of a material loses between ² and ² + d² of its energy. We can write:

P (², E) = n

dσ

(²)

d²

d² dx

= ω(², E) d² dx, (2.36)

where dσ

(²)/d² is the atomic diﬀerential cross section

∗∗

for transferring an energy

² in the interaction with an atom, n

is the number of atoms per cm

. Here

ω(², E) = n

dσ

(²)

d²

has the meaning of the diﬀerential collision probability to lose an energy between ²

and ² + d², while traversing a thickness dx.

To a ﬁrst approximation, we can neglect distant collisions which are supposed to

give small transferred energies. The expression of the diﬀerential collision probability

depends on the mass and spin of the incident particle (see Section 2.3 in [Rossi

(1964)] and references therein). For a particle with z = 1 and mass m

, kinetic

energy E

(where E

= E − m

) and energies in units of MeV, we have:

a) with spin 0

ω(², E) = 0.1535

ρZ

Aβ

1 − β

b) with spin

ω(², E) = 0.1535

ρZ

Aβ

1 − β

c) with spin 1

ω(², E) = 0.1535

ρZ

Aβ

·µ

1 − β

¶µ

1 +

¶¸

where

and ω(², E) is in (MeV cm)

−1

For ² ¿ W

(this implies ² ¿ E

and ² ¿ E) and ² ¿ E

, the diﬀerential

collision probability is reduced to:

ω(², E) = 0.1535

ρZ

Aβ

[MeV cm]

−1

. (2.37)

∗∗

The reader can see page 15 for the deﬁnition of diﬀerential cross section.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 55

Thus, when the transferred energy is very small, the diﬀerential collision probability

is given by the expression (2.37), which depends on ² and β, but is independent of

the particle spin. Only for ² larger than E

or when ² is no longer much smaller

than W

, the particle spin can play a role (as previously mentioned).

Equations (2.36, 2.37) allow an approximate calculation of the probability of

δ-ray emission

∗

. The probability G(δ, W

) to generate a δ-ray with energy larger

than W

(but ¿ E

, E, E

, W

) traversing a thickness x is:

G(δ, W

) ≈

0.1535

ρZ

Aβ

d² dx

= x

0.1535

ρZ

Aβ

d²

= 0.1535 x

ρZ

Aβ

−

≈ 0.1535 x

ρZ

Aβ

, (2.38)

where W

is in MeV.

For example, if a particle with β = 1 passes through a 300 µm thick silicon

detector (in which

≈ 0.5 and ρ = 2.33 g/cm

), the probability to emit a δ-ray

with energy larger than 100 keV is G(δ, 0.1) ≈ 5.4%. Furthermore, this formula

shows that the emission probability goes as 1/W

In the case of a particle with charge number z, the collision probability increases

by a factor z

. In addition, for ² ¿ E

, E

and E, we can again neglect the spin

dependence of the diﬀerential collision probability, which reduces to that for a mas-

sive particle with spin 0 and charge number z, and becomes the so-called Rutherford

macroscopic diﬀerential collision probability (see [Bichsel and Saxon (1975)] and re-

ferences therein):

ω(², E)

= 0.1535

ρz

Aβ

1 − β

[MeV cm]

−1

. (2.39)

Let us consider a large number N

of particles of energy E traversing a material

of thickness x. The probability f(², x) d² that the energy loss (traversing a thickness

x) is between ² and ² + d² can b e determined when an inﬁnitesimal thickness dx is

added. By traversing the additional thickness, there is an increase of the number of

particles, I

, losing an energy between ² and ²+d²: in fact, particles which have lost

less energy, still, can lose energy and, ﬁnally, reach the required amount between ²

and ² + d². From Eq. (2.36) and indicating with f(² − ²

, x) d² the probability that

traversing the thickness x the energy loss diﬀers by ²

from the required amount,

we have:

= N

∞

[f(² − ²

, x) d²] [ω(²

, E) dx] d²

∗

An example of the emission of δ-rays is shown in Fig. 6.25.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

56 Principles of Radiation Interaction in Matter and Detection

However, there will be also a decrease of particles D

because some of them, which

have already lost the required amount of energy, can lose additional energy. From

Eq. (2.36), we have:

= N

f(², x) d²

∞

[ω(²

, E) dx] d²

Let us write the total variation of the number of particles:

[f(², x + dx) − f(², x)] d² = I

− D

from which we obtain

f(², x + dx)−f(², x)=

∞

f(² − ²

, x)ω(²

, E) d²

dx−

f(², x)

∞

ω(²

, E) d²

dx,

and, ﬁnally, we ﬁnd the so-called transport equation

∂f(², x)

∂x

∞

f(² − ²

, x) ω(²

, E) d²

− f(², x) σ

(E), (2.40)

where

(E) =

∞

ω(²

, E) d²

In deriving Eq. (2.40), we have assumed that i) the diﬀerential collision probability

does not vary in a appreciable way because of the energy lost in traversing the

thickness x of material and ii) the collisions are statistically independent.

The energy straggling function is the function f(², x) which is the solution of the

integro-diﬀerential Equation (2.40), i.e., the solution of the transport equation.

2.1.2.2 The Landau–Vavilov Solutions for the Transport Equation

Solutions of the transport equation were proposed by many authors (see [Landau

(1944); Symon (1948); Blunck and Leisegang (1950); Vavilov (1957); Sternheimer

(1961); Rossi (1964); Shulek et al. (1966); Bichsel and Saxon (1975)] and references

therein).

Landau (1944) solved Eq. (2.40) by a method based on Laplace transforms for

thin absorbers, namely those for which the condition

¿ 1 is satisﬁed and where

ξ is given by:

ξ = 0.1535 x

ρz

Aβ

[MeV]. (2.41)

In the opposite case

À 1

, i.e., for thick absorbers, the function turns into a

Gaussian distribution [Landau (1944)]. In his calculations, he used the Rutherford

macroscopic collision probability for the limiting case W

→ ∞. Landau’s solution

of the transport equation is expressed as

f(², x)

φ(λ)

[MeV

−1

], (2.42)

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 57

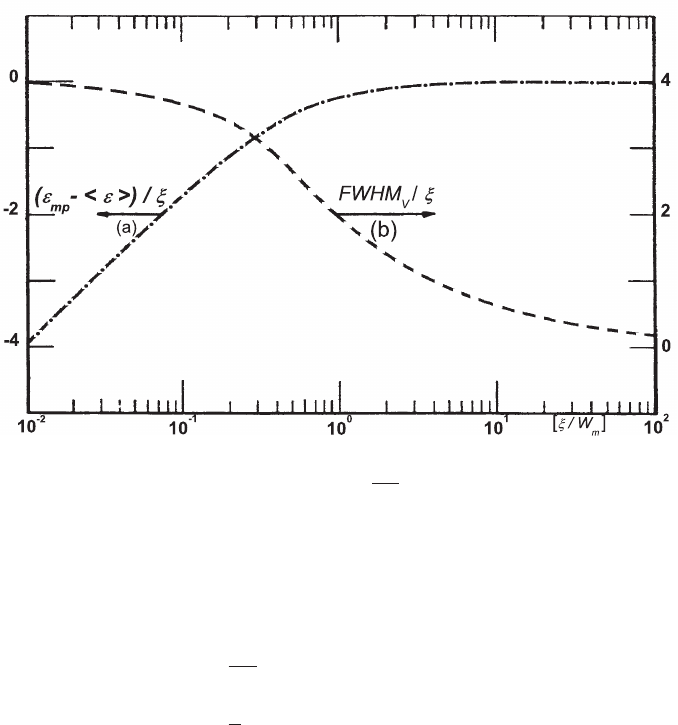
Fig. 2.9 The dashed-dotted curve (a), left hand scale, is the value of (²

− h²i)/ξ for the Vavilov

solution of the transport equation as function of

(from [Seltzer and Berger (1964)]). The

dashed curve (b), right hand scale, is the F W HM

of the Vavilov distribution in units of ξ

(adapted and reprinted with permission from [Seltzer and Berger (1964)]).

where φ(λ) (tabulated in [Bo ersch-Supan (1961)]) is a function of a universal para-

meter λ and it is given by:

φ(λ) =

2πi

r+i∞

r−i∞

exp[u ln(u) + λu] du

+∞

(−πu/2)

cos[u(ln(u) + λ)] du,

where r is an arbitrary real positive constant. f(², x)

has a maximum for

≈ −0.229 (2.43)

and a Full Width Half Maximum

F W HM

' 4.02 ξ (2.44)

(see [Rancoita and Seidman (1982)] and references therein for a more detailed dis-

cussion of these parameters). The energy loss corresponding to the maximum of

the function f(², x)

is called the most probable energy-loss (²

). This function

is characterized by an asymmetric long tail in the region well above ²

, which is

called Landau tail. This tail is mainly due to fast emitted δ-rays.

Later, Vavilov (1957) solved the equation by introducing the physical limits

coming from W

and using the Rutherford expression provided by Eq. (2.39), i.e., he

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

58 Principles of Radiation Interaction in Matter and Detection

gave the solution for:

∂f(², x)

∂x

f(² − ²

, x)

ω(²

, E)

d²

− f(², x)

ω(²

, E)

d²

where ω(²

, E)

= 0 for ²

> W

and u = ² for ² < W

and u = W

for ² >

. f(², x)

can be found tabulated in [Seltzer and Berger (1964)]. Furthermore

for

→ 0, he demonstrated that f(², x)

→ f(², x)

and that the Landau

parameter λ has the following relationship:

λ →

(² − h²i) − β

− ln

− 1 + C

, (2.45)

where C

= 0.577215 is the Euler constant and h²i is the mean energy-loss in the

material of thickness x. The mean energy-loss can be calculated using Eq. (2.17):

h²i = ξ

2mv

(1 − β

)

− 2β

− δ − U

[MeV]. (2.46)

Experimental data show that the Landau–Vavilov solutions are almost equiva-

lent for

≤ 0.06 [Aitken et al. (1969)]. For instance for 300 µm silicon detectors,

this limit is already achieved by protons with momenta larger than 550 MeV/c.

In the following, the energy straggling distribution for thin absorbers will be

indicated by f (², x)

L,V

For thick absorb ers

À 1

under the condition that the energy loss is such

that the diﬀerential collision probability does not vary in an appreciable way along

the particle path, the Vavilov energy straggling distribution becomes almost a Gaus-

sian function:

f(², x)

≈

2π W

1 −

exp





−

(² − h²i)

1 −





, (2.47)

where the standard deviation is

≈

1 −

In Fig. 2.9 (see [Seltzer and Berger (1964)]), the computed values (curve b) for

the F W HM

of the Vavilov distribution in units of ξ are shown as a function

. It can be seen that the energy-loss distribution narrows as

becomes

À 1. In the same ﬁgure (curve a), the diﬀerence between the most probable and

the mean energy-loss is also shown (see [Seltzer and Berger (1964)]). While the

mean energy-loss is larger than the most probable energy-loss for

→ 0, they

become almost equal for

À 1.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 59

2.1.2.3 The Most Probable Collision Energy-Loss for Massive Charged

Particles

As previously discussed, for thin absorbers the energy straggling distribution

f(², x)

L,V

has a maximum for λ = λ

with λ

given by Eq. (2.43). The most

probable energy-loss is obtained for λ = λ

by Eq. (2.45). It can be re-expressed as:

= h²i + ξ

+ β

+ ln

+ 1 − C

= h²i + ξ

+ ln

+ 0.194

[MeV]. (2.48)

At high energy for βγ > 10

(the parameters S

are given in Tables 2.1 and 2.2)

and β ≈ 1, the energy-loss formula is approximated by Eq. (2.26). Thus, Eq. (2.48)

becomes:

= ξ

2mc

(hν

)

− 1

+ ξ

+ 1.194

= ξ

2mc

(hν

)

+ 0.194

[MeV]. (2.49)

Equation (2.49) shows that, at relativistic energies, the most probable energy-loss

(²

) is independent of the incoming particle energy. However, it has a logarithmic

dependence on the medium thickness traversed [see Eq. (2.41)].

As an example (see Appendix A in [Rancoita and Seidman (1982)]), we can

evaluate the most probable energy-loss for silicon detectors. Using the hν

value

given in Table 2.1, Eq. (2.49) becomes

mp,Si

= ξ [ln ξ + 20.97] [MeV], (2.50)

where ξ is in MeV. This formula (see Fig. 2.10) is valid for silicon absorbers also at

relatively low βγ values (i.e., > 30). For instance, for βγ > 30 in the expression for

the density-eﬀect correction [Eq. (2.23) at page 48] the term a

ln 10

βγ

´i

is lower than 0.44 and results in the decrease of ²

mp,Si

by less than 3%. Thus, the

expression given in Eq. (2.50) extends its validity for βγ > 30, i.e., for protons

with a momentum larger than 28 GeV/c or for pions with a momentum larger than

4 GeV/c. From Eq. (2.50), in a 300 µm thick silicon detector relativistic pions and

protons will have ²

mp,Si

= 84.2 keV in agreement with experimental data [Hancock,

James, Movchet, Rancoita and Van Rossum (1983)]. Here h²

mp,Si

i is about 16%

larger than ²

mp,Si

(see [Rancoita (1984)]). Furthermore for βγ > 100, in a 300 µm

silicon detector (see Fig. 2.6), the observed most probable energy-loss (in eV/µm)

is ≈ 5% lower

than that in a 900 µm detector, in agreement, within the experi-

mental errors, with the decrease of ≈ 6.5% computed by means of Eq. (2.50). This

equation agrees with the most probable energy-losses computed, for large values of

This value is marginally aﬀected by the shift of the Landau energy-loss peak discussed at page

67.