Leroy C., Rancoita P.-G. Principles Of Radiation Interaction In Matter And Detection

Подождите немного. Документ загружается.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

70 Principles of Radiation Interaction in Matter and Detection

In Fig. 2.15 [Hancock, James, Movchet, Rancoita and Van Rossum (1984)], it is

presented the energy-loss spectrum of 1, 2, 3 and 4 relativistic particles traversing

a silicon detector, simultaneously. The production rate depends on the particle

multiplicity. The agreement between the ﬁtted (continuous) curve and experimental

data indicates that the factors ξ

, σ

I,np

and ²

mp,np

[see Eqs. (2.57, 2.59, 2.60)]

account well for multi-particle collision losses.

2.1.3 Range of Heavy Charged Particles

At low energies, but high enough for shell corrections to be neglected, relativistic

corrections are not relevant anymore and the stopping power depends on 1/v

[see

Eq. (2.2)]. Thus, for non-relativistic particles with charge ze and mass m

the

stopping power becomes, within ≈ 8%,

−

≈ 2πe

ρN

2mv

= 0.0784 ρN

2mv

[MeV], (2.61)

where

is the kinetic energy of the particle.

The dependence, conﬁrmed by experimental data, of Eq. (2.61) on both z

and

1/v

results in a large multiplicative factor for low energy charged ions. Thus, the

speciﬁc ionization, i.e., the number of charge pairs created per cm by ionization,

rises to a maximum when the particle has nearly lost all its energy. This increase

of speciﬁc ionization is referred to as the Bragg peak.

We call the mass stopping power of a material the quantity

dχ

≡ −

, (2.62)

where χ = ρx is the absorber thickness in units of g/cm

If, for a particle of charge ze and kinetic energy E

, the mass stopping power

is known [Eqs. (2.61, 2.62)] in an absorber a with thickness χ, the relative stopping

power R

in a second absorber b with the same thickness χ is given by:

2mv

¶¸Á·

2mv

¶¸

ln(2mv

)

ln(2mv

)

. (2.63)

In Fig. 2.16 [PDB (1980)], the stopping powers calculated by means of Eq. (2.1)

for various particles (up to α-particles) with kinetic energies above a few MeV’s

are shown for Pb absorbers and with an indication of the scaling factor up to

carbon. Within ≈ 8%, Eq. (2.63) can be used for determining the stopping power

in other absorbers.

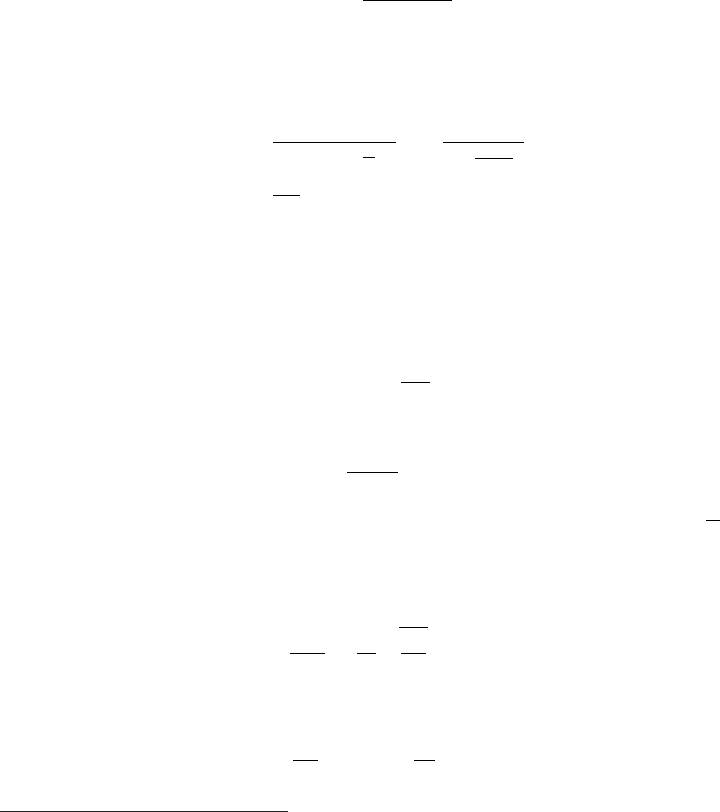
January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 71

Except for the very ﬁnal part of the particle range

∗∗

in matter, the heavy particle

path inside an absorber is almost rectilinear, and the mean range

††

can be taken

equal to the total path length, which can be obtained by integrating:

(−dE/dx)

where E

is the particle initial kinetic-energy and −dE/dx is the stopping power

(e.g., see Section 5 of [Fano (1963)] and Section 4.9.1 of [Marmier and Sheldon

(1969)]). For a non-relativistic particle using Eq. (2.61), we have:

t,m

0.1568 ρN

2mv

(2.64)

≈

f(v

), (2.65)

where v

is the particle initial velocity. Once the relationship between the range

and the kinetic-energy of a particle with charge z e and mass m

is known for an

absorber, one can determine an approximate

∗

relationship for another particle with

mass M

and charge z

e at a shifted kinetic-energy so that both particles have

equal v

-values or, equivalently,

k,M

= E

k,m

;

thus from Eq. (2.65), for the latter particle we have

t,M

k,M

≈

t,m

k,m

Bragg’s measurements show that, at such low energies, the quantity R

ρ/

√

is, within 15%, constant for every particle of given energy in diﬀerent absorbing

materials, i.e., the ratio of mean ranges in materials a and b follows the Bragg–

Kleemann rule:

t,a

t,b

≈

In the case of a mixture made of a set of elements with relative mass abundance

, the mass value to be used in the Bragg–Kleeman rule is:

∗∗

In literature (e.g. see discussion in Section 2.9 of [Fano (1963)], the range of a particle traversing

a medium can be found deﬁned as the mean path length covered before coming to rest or the mean

distance traveled along its initial direction (mean penetration depth, also termed mean projected

range). In this book, the range is usually approximated by the mean path length, if not explicitly

indicated as the mean penetration depth.

††

For ranges determined under the continuous-slowing-down approximation (csda), energy-loss

ﬂuctuations are neglected and charged particles are assumed to lose energy at a rate given by the

stopping power.

∗

It has been assumed that the I-dependence of the integral in Eq. (2.64) can be neglected.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

72 Principles of Radiation Interaction in Matter and Detection

Fig. 2.16 Mean range in g cm

−2

and stopping power in MeV g

−1

from Eq. (2.1) for various

particles in Pb, with scaling to Cu, Al and C (adapted and republished with permission from Kelly,

R.L. et al., Particle Data Group, Review of Particle Physics, Rev. of Mod. Phys. 52, S1 (1980);

For air, we have

√

air

= 3.81 and ρ

air

= 1.21 × 10

−3

g/cm

. A rough estimate of

the mean range of protons, R

, in dry air at STP between a few MeV’s and ≈ 200

MeV can be obtained by the Wilson and Brobeck formula [Wilson (1947)]:

t,air

= 10

kin

9.3

1.8

[cm],

where E

kin

is in MeV. The mean range R

t,a

in an absorber a can be calculated

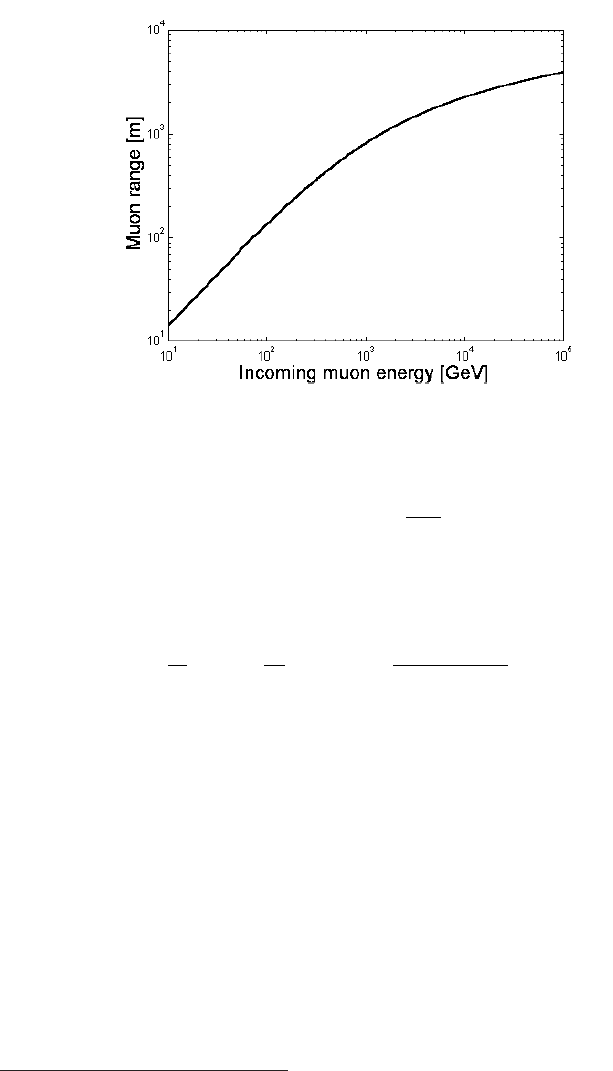
January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 73

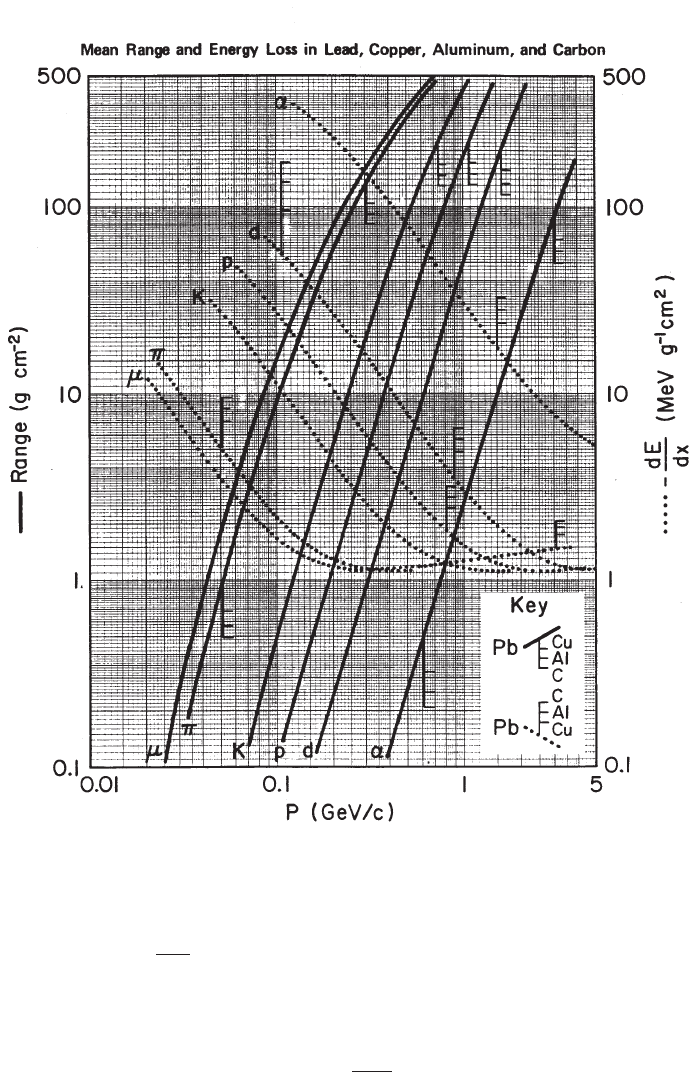
Fig. 2.17 Range of muon, in m, in standard rock computed by means of Eq. (2.66).

from that in air using the relationship:

t,a

= 3.2 × 10

−4

air

t,air

For muons (see Fig. 2.17 and [Wright (1974)]) with incoming energies larger

than 10 GeV in standard rock, with ρ = 3 g/cm

, Z = 11 and A = 22, the range is

given by:

) =

1 +

¶¸·

0.96

ln E

− 7.894

ln E

− 8.074

[g/cm

], (2.66)

where a

= 2.2 MeV/(g/cm

), b

= 4.4 × 10

−6

/g, and E

is MeV. Muon

stopping p ower and range tables are also found in [Groom, Mokhov and Striganov

(2001)].

The ranges of massive particles up to high-energies are reported in [ICRUM

(1993a); Grupen (1996); ICRUM (2005)] (see also references therein). The ranges

of protons and α-particles are available on web [Berger, Coursey, Zucker and Chang

(2005)].

Due to the statistical nature of the energy loss, not all mono-energetic particles

will have exactly the same traveled path in an absorber. To a ﬁrst approximation,

this variation, or range straggling, follows a normal (Gaussian) distribution with

a straggling parameter

‡‡

which also depends on i) the massive-particle charge and

velocity and ii) the absorber atomic number and ionization energy as discussed for

instance in [Marmier and Sheldon (1969)]). However, the path-length distribution is

skewed with a tail toward shorter-than-average path lengths, i.e., the most probable

‡‡

The straggling parameter expresses the half-width at (1/e)th height of the straggling distribution

(see Section 4.9.1 of [Marmier and Sheldon (1969)]).

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

74 Principles of Radiation Interaction in Matter and Detection

path length is slightly longer than the average value [ICRUM (1993a)] (see also

references therein). Furthermore, useful quantities are i) the projection of the range

on the particle-track initial direction, which allows one to determine the penetration

depth and ii) the ratio between the average penetration depth and average path

length (this ratio is termed detour factor).

2.1.4 Heavy Ions

By heavy ions is usually meant atoms beyond helium, which do not have a neutral

state of charge, i.e., they have a net positive charge, although negative ions can

also be generated. In literature, when their atomic number z is not À 1, they may

be also referred to as light. In addition, ions with velocity larger than the Bohr

velocity

, v

, are commonly termed swift.

When atoms or ions having velocities much larger than electron orbital velocities

go through a material, they will modify their charge state

‡

: at suﬃciently high

energies their electrons will be stripped and, as bare nuclei, they will proceed to lose

energy that results into an electronic stopping power. In fact, collision loss pro cesses

occur with atomic electrons of the absorber. Only occasionally, will incoming ions

interact with the nuclei of the medium. At the beginning, the probability of capture

of an electron is very limited. But electrons will be captured as the slowing-down

process decreases the incoming particle velocity down to values close to those of

orbital electrons. For velocities lower than the orbital velocities, the heavy ions will

spend a large fraction of the time in a neutral charge-state. In addition, at small

velocities the interaction with nuclei in the medium cannot be neglected anymore

(Sect. 2.1.4.1).

The ion velocity is usually given in a dimensionless form, like β = v/c in units

of c, or expressed as

≡

' 137.036 β,

i.e., in units of the Bohr orbital velo city (v

= e

/~ = c α) of the electron in the

hydrogen atom (see Appendix A.2); or, ﬁnally, in units of ς = ς

/z, i.e., in units of

the Bohr orbital velocity of its own K-electron.

At suﬃciently high energies, the energy-loss equation can be applied to the col-

lision process (e.g., see Sects. 2.1 and 2.1.1; in addition, see Chapter 3 of [Ziegler,

Biersack and Littmark (1985a); Ziegler, J.F. and M.D. and Biersack (2008a)]). Thus,

for ion velocities ς

À z, the stopping power increases as 1/β

with decreasing ve-

locity; while at intermediate velocities (ς

≈ z

2/3

) charge neutralization occurs

gradually and begins to dominate the velocity dependence. In fact, as already men-

tioned, the ion’s charge state do es not remain constant as it passes through an

The reader can also see Appendix A.2.

‡

The charge state of an ion refers to the instantaneous net charge of an ion.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 75

Fig. 2.18 Experimental equilibrium charge distributions for heavy ions at high velocities. The charge fractions φ

(i.e., φ

, φ

z−1

, φ

z−2

etc.) versus

the velocity expressed as ς

/z show an approximately universal relationship (adapted and reprinted, with permission, of the Annual Review of

Nuclear Science, Volume 13

° 1963 by Annual Reviews www.annualreviews.org; [Northcliﬀe (1963)], see also references therein).

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

76 Principles of Radiation Interaction in Matter and Detection

absorber and its velocity is lowered. Empirically, the energy-loss formula must be

modiﬁed by introducing the parameter ¯$(β) to weight the charge state. This para-

meter (see [Northcliﬀe (1963)] and references therein) can be obtained by energy-loss

measurements of protons and ions, with atomic number z and rest mass m

, in a

medium with atomic number Z and rest mass M (m

and M are in atomic mass

units). These measurements allow one to determine

−

ion

= −[ ¯$(β) z]

proton

with

¯$

(β) =

ζ=1

(β)

where ζ is the charge state of the ion and φ

(β) is the fraction (function of β) of

the time spent in that charge state. At energies

∗

above 1 MeV/amu, equilibrium

charge distributions φ

were measured for various ions and are shown in Fig. 2.18

([Northcliﬀe (1960)] and references therein). These data indicate that φ

(i.e., φ

z−1

, φ

z−2

etc.) has an approximate universal dependence on the velocity expressed

as ς

/z.

In the velocity region below ς

≈ z

2/3

, the electronic stopping power can be

expressed as [Lindhard and Sharﬀ (1961)]:

−

ion

= 8 κ

πe

√

2/3

+ Z

2/3

, (2.67)

where κ

is a numerical constant of order z

1/6

, a

is the Bohr radius of the hydrogen

atom and n

is the number of atoms per cm

[Eq. (1.39)].

As discussed so far, the ion eﬀective-charge varies at low velocity. The eﬀec-

tive charge of a hydrogen atom was subject of controversy; but, at present, it is

determined that protons do not have a bound electron at any velocity (e.g., see

pages 74–79 of [Ziegler, Biersack and Littmark (1985a)] and Section 3.1 of [ICRUM

(1993a)]). The charge variation is exhibited by α-particles: for example, Figure 3.1

of [ICRUM (1993a)] shows that this eﬀect decreases the stopping power

‡‡

in water

and gold at kinetic energies below ≈ 1.2 MeV. A literature survey on the electro-

nic stopping p ower of ions with non-constant charge state is given in Section 3.4

of [ICRUM (2005)].

A comparison with experimental data, and a description of computer codes using

the Monte-Carlo technique for evaluating both the electronic stopping power and

the range of heavy ions are given in [Ziegler, Biersack and Littmark (1985a); Ziegler,

J.F. and M.D. and Biersack (2008a)] (see also: [ICRUM (1993a)], for protons and

α-particles, [ICRUM (2005)], for heavier ions and Chapter 7 of [Sigmund (2006)]).

∗

The reader can ﬁnd the deﬁnition of kinetic energies per amu in Sect. 1.4.1.

‡‡

Figure 3.1 of [ICRUM (1993a)] also shows that the Barkas eﬀect (see Sect. 2.1.1.1) increases the

α-particle stopping power in gold by . 4% for kinetic energies above ≈ 2 MeV, but it is negligible

in water.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 77

Fig. 2.19 Universal nuclear stopping power (adapted and reprinted, with permission,

of the Annual Review of Nuclear Science, Volume 13

° 1963 by Annual Reviews

www.annualreviews.org; [Northcliﬀe (1963)]) for heavy ions velocities ς

≤ 1. The straight line

is the electronic stopping power for N

in Al computed by means of Eq. (2.67). The or-

dinate axis is for the stopping power −

dχ

ion

in units of MeV cm

−1

multiplied by

zZm

+ M)

2/3

+ Z

2/3

. The units for the abscissa axis are:

M/(m

+M)

√

2/3

2.1.4.1 Nuclear Stopping Power

At low velocity (ς

. 1), i.e., when the charge neutralization begins to dominate

the collision energy-loss process, the ion electronic stopping power decreases and the

energy loss due to collisions with target nuclei is no longer negligible. This latter

process results in the so-called nuclear stopping power

∗

(e.g., see Sect. 4.2.1.1; in

addition, see Chapter 2 of [Ziegler, Biersack and Littmark (1985a); Ziegler, J.F.

and M.D. and Biersack (2008a)] and references therein). As the electronic stopping

power decreases rapidly, the nuclear stopping power increases approximately as

1/β

. At a critical velocity

0,c

¿ 1,

the nuclear stopping power exceeds the electronic stopping power. However, at very

low velocities when the screening of the nuclear ﬁeld of ions and atoms is dominant,

the nuclear stopping power reaches a maximum and starts to fall (Fig. 2.19). To a

∗

This process is mainly resp onsible for displacement damage in semiconductors (e.g., see

Sects. 4.2.1, 4.2.1.1 and 4.2.1.3).

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

78 Principles of Radiation Interaction in Matter and Detection

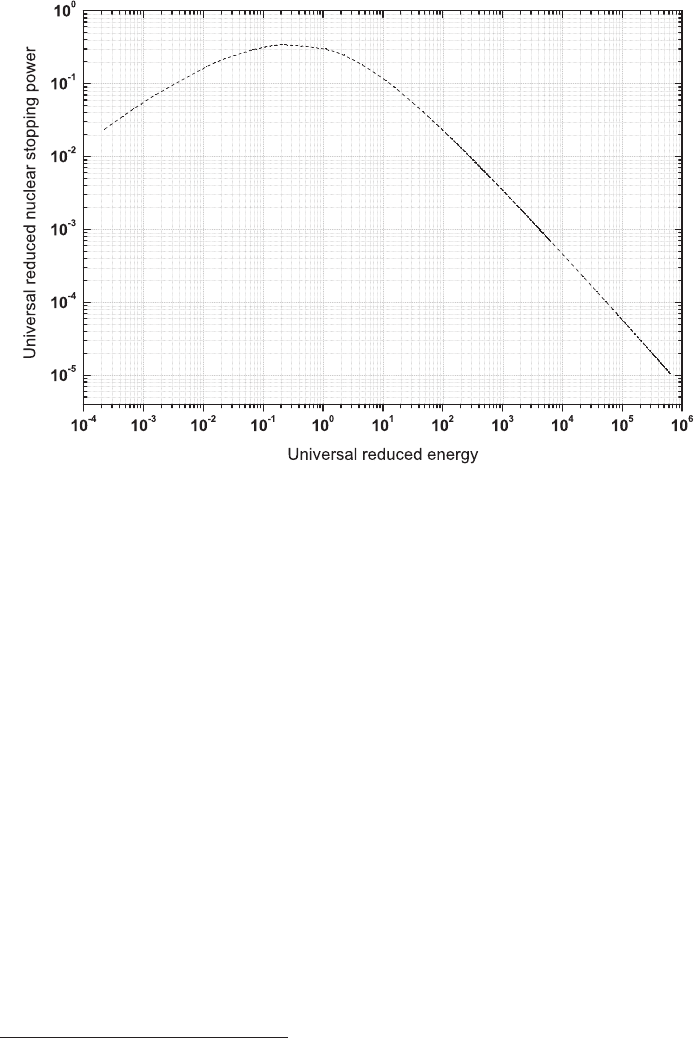
Fig. 2.20 Universal reduced nuclear stopping power [R(²

r,U

)] as a function of the universal re-

duced energy (²

r,U

ﬁrst approximation, the nuclear stopping power can be represented by the universal

curve given in Fig. 2.19 ([Northcliﬀe (1963)] and references therein). In this ﬁgure,

z and m

are the charge and the mass of the incoming ion, respectively; Z and M

are the charge and the mass of the absorber atoms, respectively; ﬁnally, E

is the

kinetic energy of the incoming ion in units of MeV and the path length χ

is in units

of mg/cm

. A detailed comparison of models, a comparison with experimental data,

and a description of computer codes using the Monte-Carlo technique for evaluat-

ing the nuclear stopping powers for heavy ions are given in [Ziegler, Biersack and

Littmark (1985a); Ziegler, J.F. and M.D. and Biersack (2008a)] (see also Section 4

of [ICRUM (1993a)]). In addition, a review of the properties of ion interaction with

matter is found in [Balanzat and Bouﬀard (1993)].

As mentioned above, the energy lost to target nuclei is basically determined

by investigating screened Coulomb collisions between two interacting atoms

†

with

almost non-relativistic velocities. Using the Thomas–Fermi model of the atom

(e.g., see Chapters 1 and 2 of [Torrens (1972)]), the scattering of the projectile

by target atoms can be treated in terms of an interatomic Coulomb potential which

is a function of the radial distance r between the two nuclei {e.g., see Equation (3.9)

†

The reader can ﬁnd a survey dedicated to interatomic potential treatment in [Torrens (1972)]

(see also [Gehlen, Beeler and Jaﬀee (1972)]).

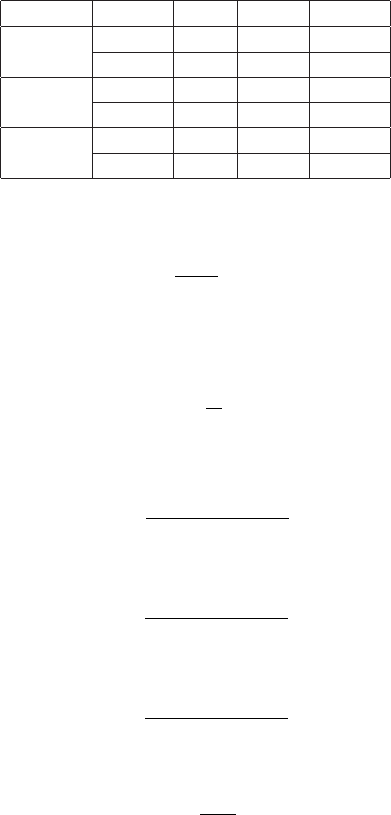
January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 79

Table 2.4 Nuclear stopping power fractions in per-

centage at 1, 10 and 100 keV in Be, Si and Pb

absorber for protons (p) and α-particles (α) (data

from [Berger, Coursey, Zucker and Chang (2005)]).

Absorber Particle 1 keV 10 keV 100 keV

p 15.0 1.3 0.2

α 53.3 12.7 1.0

p 10.2 1.4 0.2

α 61.0 17.5 1.3

p 5.1 1.5 0.2

α 22.9 10.1 1.8

of [Torrens (1972)] or Equation (2-56) of [Ziegler, Biersack and Littmark (1985a)]}

V (r) =

zZe

), (2.68)

where ez (projectile) and eZ (target) are the charges of the bare nuclei and Ψ

is the

interatomic screening function. This latter function depends on the reduced radius

given by

, (2.69)

where a

is the screening length (also termed screening radius). Several expressions

were suggested for a

, e.g., by Bohr (1940)

2/3

+ Z

2/3

1/2

, (2.70)

by Firsov (1957)

1/2

+ Z

1/2

2/3

, (2.71)

and, also, by Lindhard and Sharﬀ (1961)

2/3

+ Z

2/3

1/2

, (2.72)

where

is the Bohr radius (see App endix A.2), m is the electron rest mass and

9 π

1/3

−7/3

' 0.88534

is a constant introduced in the Thomas–Fermi model.

The interatomic potentials [Eq. (2.68)] accounting for the electron clouds of the

projectile and target nuclei were calculated by various authors, who provided ex-

pressions for the screening functions (e.g., see pages 33–41 of [Ziegler, Biersack and