Leroy C., Rancoita P.-G. Principles Of Radiation Interaction In Matter And Detection

Подождите немного. Документ загружается.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

100 Principles of Radiation Interaction in Matter and Detection

The average radiation loss per cm for an electron with initial energy E

, the

so-called energy-loss by radiation, is given by

−

rad

hν

hν Φ

e−n

, hν) d(hν)

= n

rad

[MeV/cm], (2.101)

where E

is in units of MeV, n

= Nρ/A is the number of atoms per cm

, and Φ

rad

is:

rad

hν

hν Φ

e−n

, hν) d(hν) [cm

/nucleus]. (2.102)

In the energy region

¿ E

¿ 137 mc

−1/3

the screening can be neglected [Heitler (1954); Bethe and Ashkin (1953)]. Using

Eq. (2.98) and after integration of Eq. (2.102), for no screening we have

rad

4 ln

−

[cm

/nucleus], (2.103)

where

Φ is given by:

Φ = αZ(Z + 1) r

= 5.8 × 10

−28

× Z(Z + 1) [cm

]. (2.104)

In the energy region

À 137 mc

−1/3

the screening is almost complete [Heitler (1954); Bethe and Ashkin (1953)] except

for the production of energetic photons [see Eq. (2.92)]. Using Eq. (2.100) and after

integration of Eq. (2.102), for complete screening we have

rad

4 ln

183

1/3

[cm

/nucleus], (2.105)

where

is given by:

= αZ(Z + ι) r

= 5.8 × 10

−28

× Z(Z + ι) [cm

]. (2.106)

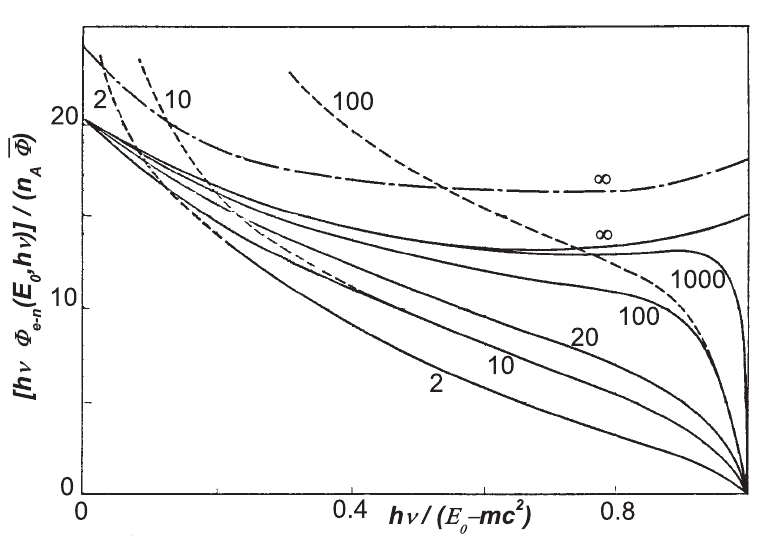
The energy or intensity distribution of the bremsstrahlung is obtained by multiply-

ing the emitted photon energy (hν) by the diﬀerential probability energy distribu-

tion per nucleus, i.e.,

hν

e−n

, hν)

d(hν),

where the expression for Φ

e−n

, hν) depends on the screening conditions as dis-

cussed above. In Fig. 2.29, [hν Φ

e−n

, hν)]/(n

Φ) is shown as a function of

hν/(E

− mc

). The function

hν Φ

e−n

, hν)

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 101

is the energy distribution per unit of photon energy interval divided by

Φ [see

Eq. (2.104)]. The dotted curves are calculated assuming that the screening can be

neglected and are valid for all elements, b ecause the Z dependence is contained in

the term

Φ only. The full curves are for lead, except for the non relativistic energy

case whose curve refers to aluminum. As the primary energy increases, the screening

is almost complete; the curve marked ∞ is for complete screening. In the region

of high-energy photon emission, the screening can be neglected and the curves are

those for no screening. At high energies, the [hν Φ

e−n

, hν)]/(n

Φ) distribution

shows an approximate ﬂat central region above 0.4 before dropping near to 1: this

indicates that Φ

e−n

, hν) behaves like 1/hν. Reviews on bremsstrahlung emission

are found in [Koch and Motz (1959); Berger and Seltzer (1964); Tsai (1974); ICRUM

(1984b)].

In general, the Born approximation meets diﬃculties to be applied when the

atomic number of the target nucleus increases, the initial electron kinetic energy is

low and, also, when the photon energy approaches the high-frequency limit ν

. How-

ever, these formulae are in a reasonable agreement with data, except in the high-

frequency limit. Exact theoretical calculations are available in the high-frequency

limit and agree reasonably well with experimental data [Fano et al. (1959)]. Other-

wise, modiﬁcations are proposed on the base of experimental data.

For low energy electrons (with kinetic energies lower than 2 MeV), the Elwert

factor f

[Elwert (1939)] is applied to multiply the diﬀerential probability energy

distribution (see Table V in [Koch and Motz (1959)], and also [Berger and Seltzer

(1964); Pratt et al. (1977)]):

[1 − exp(−2παZ/β

)]

β[1 − exp(−2παZ/β)]

where β and β

are the ﬁnal and initial electron velocities, respectively, in units of

speed of light.

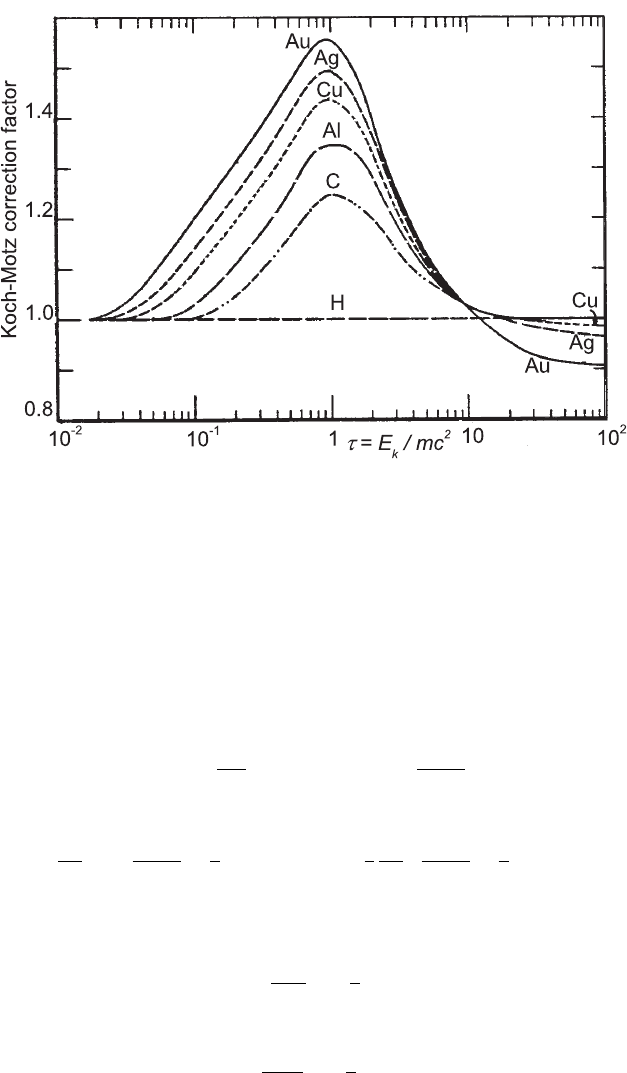
At intermediate kinetic energies (up to ≈ 50 MeV), an empirical Koch–Motz

correction factor is used (see Table V in [Ko ch and Motz (1959)] and also [Berger

and Seltzer (1964)]). This multiplicative factor is shown in Fig. 2.30 from [Berger

and Seltzer (1964)].

Above 50 MeV, the so-called extreme relativistic region, cross section calculations

with relativistic Coulomb wave functions (Sommerﬁeld–Maue) including screening

corrections were derived by Olsen (1955). The computed formula has an additive

correction factor to the Born approximation formulae described above. The diﬀe-

rential radiation probability for the nuclear ﬁeld is still given by Eq. (2.93), but the

function F (E

, hν, η) has to be rewritten as

1 +

(η)

−

ln Z − f(Z)

−

(η)

−

ln Z − f(Z)

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

102 Principles of Radiation Interaction in Matter and Detection

Fig. 2.29 [hν Φ

e−n

, hν)]/(n

Φ) as a function of hν/(E

−mc

) (adapted and reprinted with permission from [Bethe and Ashkin (1953)]). The

numbers labelling the curves indicate the electron energy in units of mc

. The solid curves are for lead and include the screening eﬀect. The dotted

curves are without screening and valid for all Z (see page 101).

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 103

Fig. 2.30 Empirical Koch–Motz correction factor as a function of τ = E

/mc

for kinetic electron

energies up to 50 MeV (adapted and reprinted with permission from [Berger and Seltzer (1964)]).

where the function f(Z) is given by (see [Davies, Bethe and Maximon (1954)])

f(Z) =







1.2021 (α Z)

, for low-Z,

0.925 (α Z)

, for high-Z;

(2.107)

for 0 < η < 2, ϕ

(η) and ϕ

(η) are shown in Fig. 2.27 while, for η > 2, they are

given by Eq. (2.95). Finally, we have

Φ(E

, hν) d(hν) = 4 α

Nρ

S(η, Z, E, E

)

d(hν)

hν

[cm

−1

], (2.108)

where S(η, Z, E, E

) is given by:

1 +

(η)

−

ln Z − f(Z)

−

(η)

−

ln Z − f(Z)

The corresponding total radiation cross section becomes [Koch and Motz (1959)]:

for no screening

rad

= 5.8 × 10

−28

× Z

4 ln

−

− f(Z)

[cm

/nucleus] (2.109)

and for complete screening

rad

=5.8 × 10

−28

× Z

4 ln

183

1/3

− f(Z)

[cm

/nucleus]. (2.110)

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

104 Principles of Radiation Interaction in Matter and Detection

For kinetic electron energies above ≈ (10–20) MeV, the most adequate formulae

are i) Eq. (2.108) for η < 15, while ii) Born approximation formulae are better for

η > 15 [Berger and Seltzer (1964)]. It has to be noted that, to a ﬁrst approximation,

in the formulae for the diﬀerential probability distribution and total radiation cross

sections, the term Z

has be replaced by Z(Z + 1) in order to take into account the

interaction on the ﬁeld of atomic electrons [Berger and Seltzer (1964)]. Koch and

Motz (1959) stated that at relativistic energies and for complete screening the best

parametrization is Z(Z + ι), where:

ι =

530/Z

2/3

183/Z

1/3

+ 1/18

In addition, for the radiative loss these formulae based on the Born approxi-

mation are expected to hold for both electrons and positrons [Berger and Seltzer

(1964); Tsai (1974)].

It has to be noted that some diﬀerences are expected in the bremsstrahlung

processes of electrons and positrons, because electrons are attracted by posi-

tive charged nuclei and repelled by atomic electrons; whereas the opposite oc-

curs for incoming positrons. However, as previously discussed, the cross sections

for electron- and positron-bremsstrahlung exhibit negligible diﬀerences at high-

energy. At low energy

∗

, the positron–nucleus cross-section is smaller than that for

electrons (e.g., see [Feng, Pratt and Tseng (1981); ICRUM (1984b); Kim, Pratt and

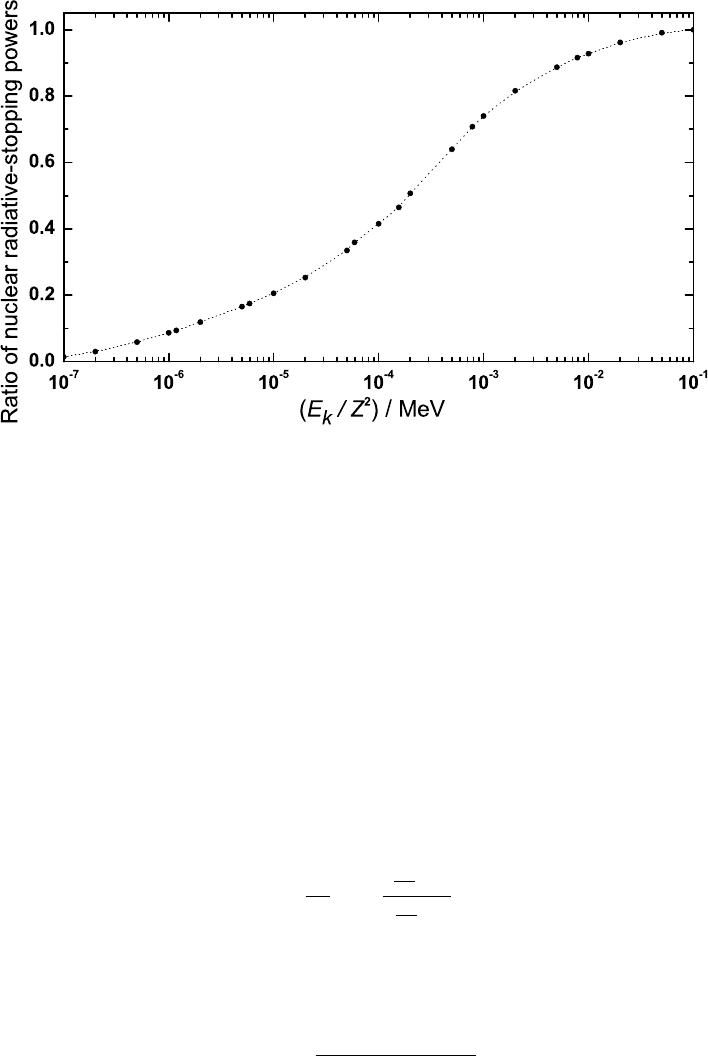
Seltzer (1984)]); the ratio

(dE/dx)

rad,n

(dE/dx)

−

rad,n

of the positron [(dE/dx)

rad,n

] and electron [(dE/dx)

−

rad,n

] radiative-stopping powers,

due to the interactions with the nuclear ﬁeld, is lower than 0.962 [ICRUM (1984b)]

for E

. 2 × 10

−2

MeV, where E

is electron and positron kinetic energy in

MeV and Z the atomic number of the medium (Fig. 2.31).

2.1.7.1 Collision and Radiation Stopping Powers

Calculated collision stopping powers (dE/dχ)

−

(where χ is in units of g/cm

) and

radiation stopping powers (dE/dχ)

−

rad

for electrons are available in [Berger, Coursey,

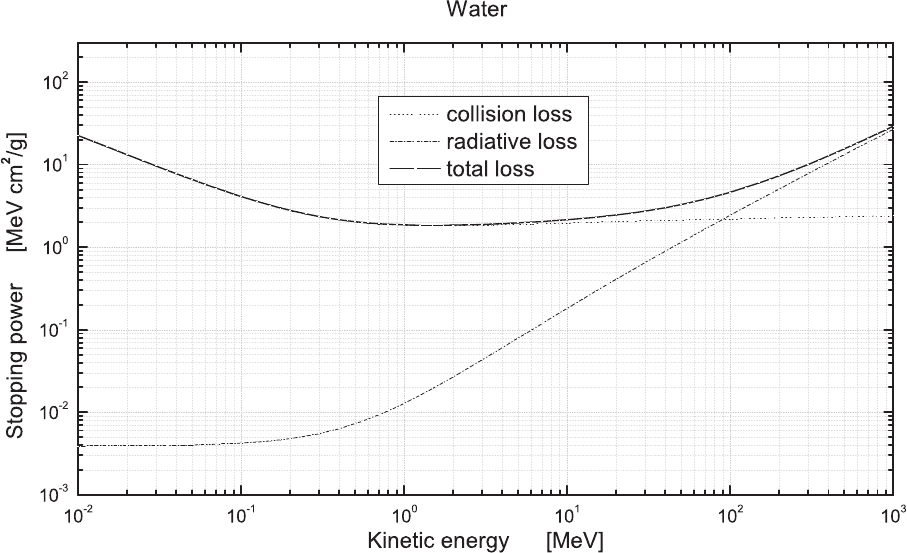
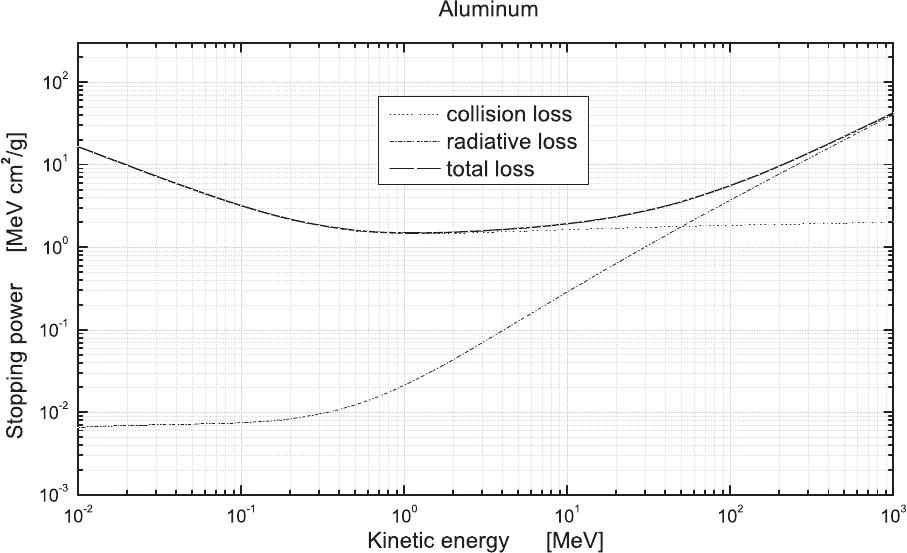
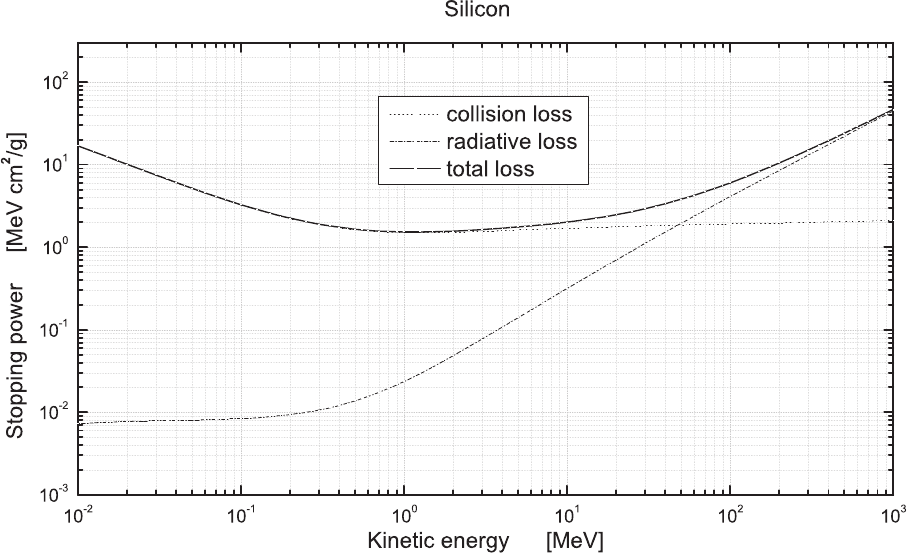
Zucker and Chang (2005)] and are shown in Figs. 2.32–2.37 for (liquid) water, Al,

Si, Fe, W and Pb, respectively.

The uncertainties on these calculated collision stopping powers are estimated

to be (1–2)% above 100 keV, (2–3)% in low-Z materials and (5–10)% in high-Z

materials between 10 and 100 keV. While in [Berger, Coursey, Zucker and Chang

(2005)] the radiative stopping powers are evaluated with a combination of theoretical

∗

At low energy, the screening eﬀect becomes less important [see Eq. (2.92)] for the radiation

energy-loss mechanism, which is dominated by photon emission resulting from the interactions in

the nuclear ﬁeld (e.g., see Figure 9.2 of [ICRUM (1984b)]).

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 105

Fig. 2.31 Ratio (R

, see text) of the positron [(dE/dx)

rad,n

] and electron [(dE/dx)

−

rad,n

]

radiative-stopping powers due to the interactions with the nuclear ﬁeld as a function of

/MeV, where E

is the electron and positron kinetic energy in MeV and Z the atomic

number of the medium {data point (•) from [ICRUM (1984b)]}. The line is to guide the eye.

bremsstrahlung cross sections described in [Seltzer and Berger (1985)], analytical

formulae (using a high-energy approximation) are used above 50 MeV, and accurate

numerical results are used from [Pratt et al. (1977)] below 2 MeV. The uncertainties

on these calculated radiative stopping powers are estimated to be 2% above 50 MeV,

(2–5)% between 2 and 50 MeV, and 5% below 2 MeV.

2.1.7.2 Radiation Yield and Bremsstrahlung Angular Distribution

The radiation yield, Υ(E

), is the fraction of the electron energy radiated by an elec-

tron with initial kinetic energy E

for bremsstrahlung emission during the slowing-

down process. Under the assumption of a continuous emission, it is given by:

Υ(E

) =

rad

tot

, (2.111)

where (dE/dx)

tot

is the total energy-loss, which includes both the radiative and the

collision losses.

An approximation for the radiation yield was derived by Koch and Motz (1959):

Υ(E

) =

3 × 10

−4

× Zτ

1 + 3 × 10

−4

× Zτ

, (2.112)

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

106 Principles of Radiation Interaction in Matter and Detection

Fig. 2.32 Total, collision and radiation stopping powers in units of MeV cm

/g as a function of the incoming electron kinetic energy in units of

MeV in (liquid) water (data from [Berger, Coursey, Zucker and Chang (2005)]).

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 107

Fig. 2.33 Total, collision and radiation stopping powers in units of MeV cm

/g as a function of the incoming electron kinetic energy in units of

MeV in Al (data from [Berger, Coursey, Zucker and Chang (2005)]).

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

108 Principles of Radiation Interaction in Matter and Detection

Fig. 2.34 Total, collision and radiation stopping powers in units of MeV cm

/g as a function of the incoming electron kinetic energy in units of

MeV in Si (data from [Berger, Coursey, Zucker and Chang (2005)]).

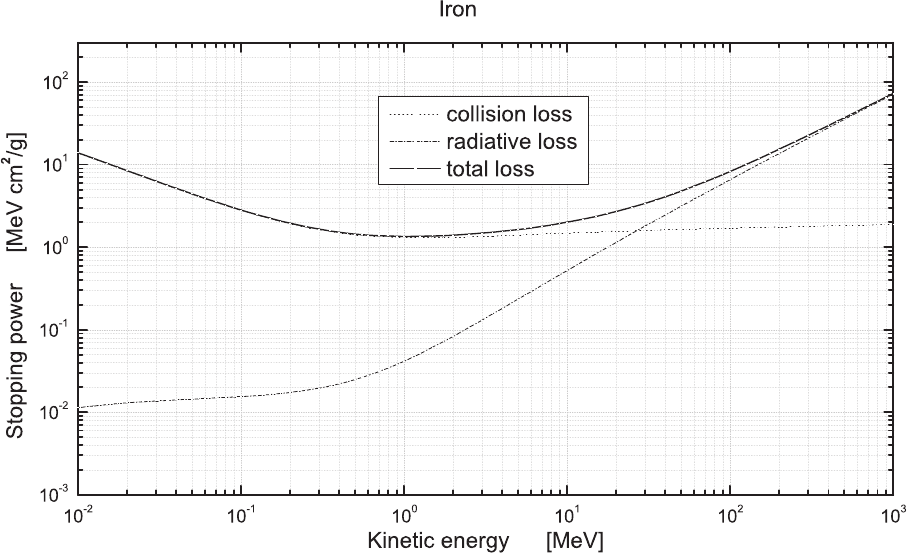
January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 109

Fig. 2.35 Total, collision and radiation stopping powers in units of MeV cm

/g as a function of the incoming electron kinetic energy in units of

MeV in Fe (data from [Berger, Coursey, Zucker and Chang (2005)]).