Leroy C., Rancoita P.-G. Principles Of Radiation Interaction In Matter And Detection

Подождите немного. Документ загружается.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

90 Principles of Radiation Interaction in Matter and Detection

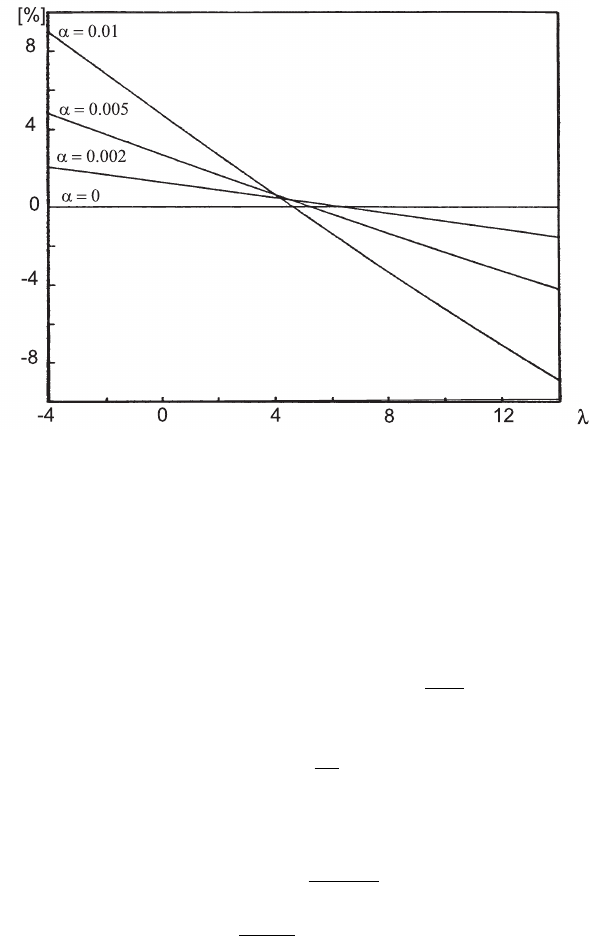
Fig. 2.24 Percentage corrections to the Landau curve for diﬀerent values of α

= c

(ξ/E

)

versus the Landau parameter λ (adapted and republished with permission from Rohrlich, F. and

Carlson, B.C., Phys. Rev. 93, 38 (1954); Copyright (1954) by the American Physical Society).

For energetic positrons and electrons traversing thin absorbers, the Møller and

Bhabha cross sections replace the Rutherford cross section. Following the Laplace

transform method and Landau’s approach for solving the transport equation (2.40),

the probability density function is given by [Rohrlich and Carlson (1954)]:

f(², x)

L,±

= exp

−α

(λ + ln α

)

φ(λ)

, (2.82)

where

= c

For c

→ 0, Eq. (2.82) reduces to Eq. (2.42). The parameters c

depend on E

and

are given by:

= β

2 −

(γ + 1)

−

2γ − 1

Their values are between ' 2 (at high energies) and ' 0 (at low energies) for c

while between 0 and 1 for c

−

(Fig. 2.23).

In Fig. 2.24 (see [Rohrlich and Carlson (1954)]), the percentage correction to the

Landau curve is given as a function of α

: for α

< 0.001 corrections to the Landau

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 91

energy-loss distribution are negligible, i.e., Eq. (2.82) reduces to Eq. (2.42). For

instance for a silicon detector 300 µm thick and β ≈ 1, ξ is ≈ 5.3 keV, namely

< 0.001 for electrons or positrons above 10 MeV. At lower energies or thicker

detectors, corrections can become relevant.

The most probable energy-loss ²

of the energy straggling distribution [see

Eq. (2.82)] occurs at a value λ

given by:

≈ λ

− 2.8 α

, (2.83)

where λ

is the value of λ at which the Landau curve [Eq. (2.42)] has the peak. Fur-

thermore, the most probable energy-loss is shifted from that one, ²

mp,Landau

[Eq. (2.48)], of the Landau distribution by:

∆²

= ²

mp,Landau

− ²

≈ 2.8 α

ξ.

For instance for a silicon detector 300 µm thick and β ≈ 1, this shift is < 1 keV

for electrons above 2 MeV: ²

was measured to be ≈ 86 keV for electrons between

(0.8−3) MeV [Hanco ck, James, Movchet, Rancoita and Van Rossum (1983)].

There is also a shrinkage of the energy-loss distribution: the F W HM

variation

with respect to the FWHM of the Landau distribution for massive charged particles

(see page 57), 4

F W HM

, is given by:

F W HM

= F W HM

− F W HM

= 6.6 α

ξ. (2.84)

For instance, in a thick silicon detector 300 µm, α

< 0.001 for electrons or positrons

above 10 MeV. Thus, the energy-loss curve is narrowed by ≈ 0.2%. In thin detectors,

the slight shrinkage can be understood by the fact that mostly small (with respect

to W

) energy transfers contribute to the build up of the most probable energy-loss.

2.1.6.3 Practical Range of Electrons

Below the critical energy, electrons mainly lose energy by collisions. However, their

ﬁnal path in matter diﬀers from that of heavy particles because they undergo large

angular scatterings. At low incoming momentum (for instance ¿ mc), it is of the

order of ≈ m/m

the transferred energy by massive particles of mass m

[see

Eq. (1.26)]. While in a Møller collision, an electron can lose up to half of its ki-

netic energy. This large amount of energy straggling inside an absorber is directly

related to the large deviations in the path of the electrons (and positrons).

A calculation of the mean path length is not meaningful in the case of elec-

trons. Along the incoming direction, the mean penetration depth is much less than

the mean path. The absorption curve

∗

for mono-energetic electrons shows typically

a long straight portion down to fairly low intensities and large penetration depths,

∗

The absorption curve is the distribution of emerging-electrons (also termed transmitted elec-

trons) percentage as a function of absorber thickness (e.g., see [Katz and Penfold (1952)]

and Section 1.1.5.4 of [Sternheimer (1961)]) or it can represent a depth-absorbed-dose curve

(e.g., see [ICRUM (1984a)] and [Sorcini and Brahme (1994)]).

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

92 Principles of Radiation Interaction in Matter and Detection

electron kinetic energy (MeV)

range (g/cm

)

0.01 0.1 1 10 20

0.0001

0.001

0.01

0.1

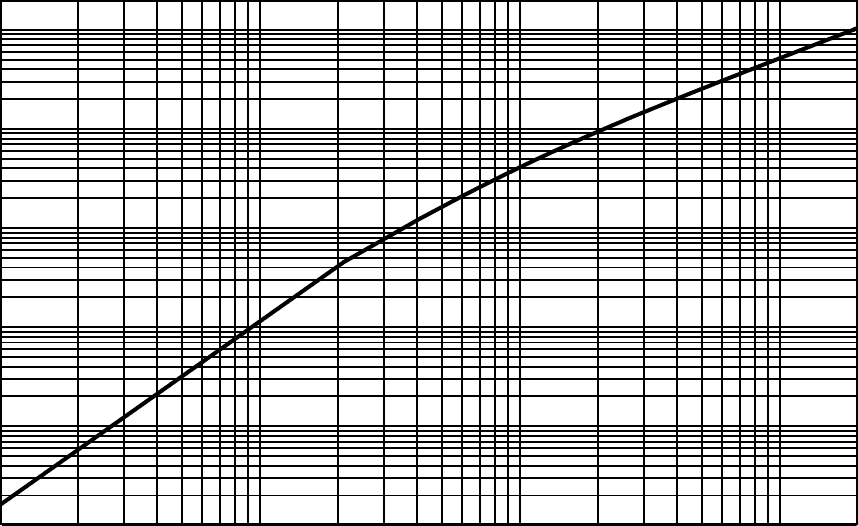
Fig. 2.25 Practical range in g/cm

for electrons calculated by means of Eqs. (2.85, 2.86).

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 93

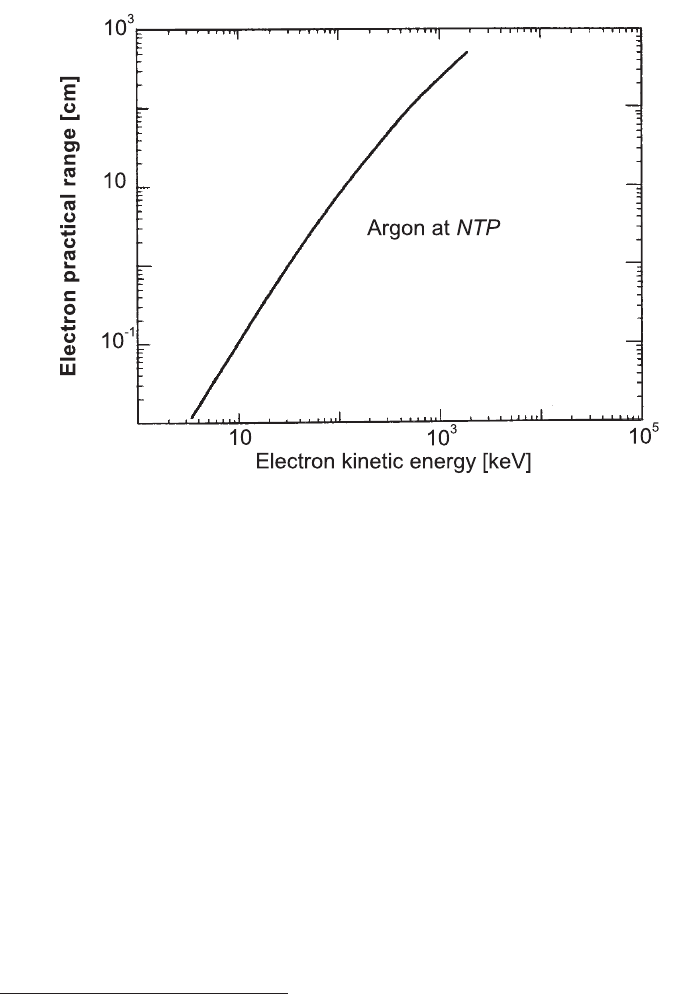
Fig. 2.26 Practical range in cm for soft electrons in Ar at NTP (adapted and reprinted with

permission from [Sauli (1977)]).

when plotted in a linear scale. The linear extrapolation of the absorption curve

†

determines the so-called practical electron range R

. Beyond R

, only a few per-

cent of the incoming electrons are left to be absorbed. Empirical expressions for the

practical range, in units of g/cm

, were proposed for diﬀerent kinetic-energy inter-

vals in MeV by various authors [Glendenin (1948); Katz and Penfold (1952)]. The

following expressions (determined using aluminum absorbers) are from [Katz and

Penfold (1952)]:

= 0.412 E

(0.01 < E < 3 MeV), (2.85)

where E (in MeV) is the electron kinetic energy,

s = 1.265 − 0.0954 ln E;

and up to 20 MeV

= 0.530 E − 0.106 (2.5 < E < 20 MeV). (2.86)

For electron energies where the radiation energy-loss is not a signiﬁcant part

of the energy-loss process, the practical ranges of electrons in units of g/cm

are

†

In these measurements, the point at which the absorption curve encounters the background

is called range (e.g., see [Glendenin (1948); Katz and Penfold (1952)] and also Section 1.1.5.4

of [Sternheimer (1961)]).

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

94 Principles of Radiation Interaction in Matter and Detection

almost independent of the atomic mass-number of the absorber; thus, to a ﬁrst

approximation {e.g., see Equation (1-21) in Section 1-10 of [Price (1964)]} we have

p,Z

≈ R

p,Z

. (2.87)

The practical range

††

of electrons with kinetic energies between 10 keV and

20 MeV is shown in Fig. 2.25. It has to be noted that typical silicon detector thick-

nesses are between 300 and 400 µm and, thus, able to absorb δ-rays up to energies

of ≈ 300 keV.

Figure 2.26 shows the practical range [Sauli (1977)] of soft electrons from ≈ 3 keV

in argon gas at Normal Temperature (i.e., 20

◦

C) and Pressure (i.e., at atmospheric

pressure), i.e., at NTP condition. As it can be noted, typical counter devices having

1 cm gas path can absorb δ-rays up to energies of ≈ 30 keV.

For applications of therapeutic electron beams, an expression

‡

used to convert

an arbitrary solid phantom-material range into a water-equivalent assumes that, in

an absorber, the range is proportional to the reciprocal of the electron density. In

water, the relationship between the practical range (in units of g/cm

) and electron

kinetic-energy (in units of MeV) is

= 0.22 + 1.98 R

p,w

+ 0.0025 R

p,w

(2.88)

(from [ICRUM (1984a)] and [ASTM (2003)]). Subsequently, for electron kinetic

energies between 0.3 and 25 MeV, modiﬁed expressions for the ranges in water

p,w

) and polystyrene (R

p,pol

) were proposed by Cleland, Lisanti and Galloway

(2004):

= 0.564 + 1.957 R

p,w

− 0.231 R

−0.130

p,w

+ 0.0030 R

p,w

(2.89)

= 0.522 + 1.846 R

p,pol

− 0.189 R

−0.155

p,pol

+ 0.0045 R

p,pol

. (2.90)

An expression for practical range can also be obtained using its relationship with

the continuous-slowing-down approximation range r

(see footnote at page 71) in

a material. Scaling laws were proposed by diﬀerent authors (e.g., [Harder (1970);

Andreo, Ito and Tabata (1992); Halbleib, Kensek, Mehlhorn, Valdez, Seltzer and

Berger (1992); Zheng-Ming and Brahme (1993); Sorcini and Brahme (1994); Tabata,

Andreo and Ito (1994)]). Based on the transport theory for energy deposition of

electrons, Harder (1970) suggested that the practical range scales (e.g., see also

[Zheng-Ming and Brahme (1993); Sorcini and Brahme (1994)]) as

= r





0.30 ×

hZi

1.31

+ 0.83





−1

, (2.91)

where τ is the electron kinetic energy in units of the electron rest mass and hZi is the

mean atomic number of the material. Equation (2.91) is valid for electron energies

††

It is calculated by means of Eqs. (2.85, 2.86) and it is in units of g/cm

‡

The reader may see Equation 12 in [Sorcini and Brahme (1994)] (see also Equation 4 in [NACP

(1980)] and references therein). In the same reference, other approximate expressions are discussed

in view of these applications.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 95

from 5 up to 30 MeV and for materials with atomic number 4 ≤ Z ≤ 82. Practical

ranges are reported in [Sorcini and Brahme (1994)] for electrons in a kinetic-energy

range of (1–50) MeV in Be, C, H

O, Al, Cu, Ag and U.

2.1.7 Radiation Energy-Loss by Electrons and Positrons

When electron (or positron) energies exceed a few tens of MeV, the dominant me-

chanism of energy loss is by emitting photons, i.e., by radiative energy-loss. It is

usually called emission by synchrotron radiation when occurring for circular accel-

eration or by bremsstrahlung when traversing matter.

The emission of electromagnetic radiation accompanies the acceleration or decel-

eration of charged particles. Assuming a uniform acceleration during the radiative

diﬀusion, the radiated energy can be easily evaluated in the framework of the clas-

sical calculation of an electromagnetic-dipole radiation emission, as for the case of

the Thomson scattering for unpolarized radiation discussed in Sect. 2.3.2.3 (see also

Chapter 4 of [Marmier and Sheldon (1969)]). The radiation emitted per unit of time

depends quadratically on the velocity variation, i.e.,

2 e

3 c

d~v

and extends over a continuous range of frequencies. In the case of bremsstrahlung

emission by a particle with charge number z and mass m

in an absorber with

atomic number Z, the acceleration

d~v

depends on zZe

, thus:

∝

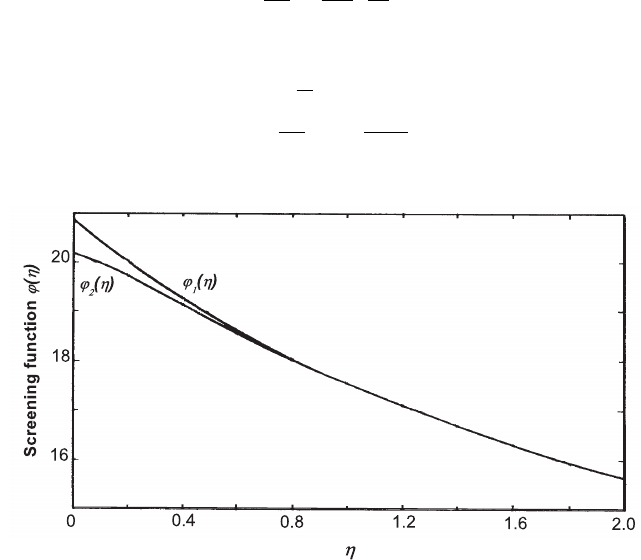
Fig. 2.27 Screening functions ϕ

(η) and ϕ

(η) versus η [Marmier and Sheldon (1969)] (see

also [Bethe and Heitler (1934)]).

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

96 Principles of Radiation Interaction in Matter and Detection

As a consequence, the bremsstrahlung intensity depends on z

, while the collision

energy-loss depends on Z (i.e., on the number of electrons per cm

) as shown in

Eq. (2.1), and inversely on the square of the incoming particle mass. For this latter

reason, it is much less probable that a massive charged particle (π, K, proton,

etc.) radiates photons traversing a medium than an electron or a positron. It has

to be noted that the energy emitted by radiation depends on Z

. However, in the

interactions inside a medium, there is an additional contribution due to the Coulomb

ﬁeld of the Z atomic-electrons, each one with charge 1, thus providing an overall

Z-dependent contribution.

The probability of radiation depends, in an essential way, on the eﬀective dis-

tance between the electron and the nucleus. In a classical description of the inte-

raction, when the impact parameter is much larger than the atomic radius, the

eﬀective nuclear charge is screened by the atomic electrons and the nuclear ﬁeld

greatly loses its eﬀect on the incoming particle, because the ﬁeld of outer electrons

has to be taken into account. This is referred to as complete screening. Conversely,

for impact parameters that are small with respect to the atomic radius, we expect

no screening eﬀect, namely the ﬁeld acting on the incoming particle can be approxi-

mated with the Coulomb ﬁeld of a point charge Ze at the center of the nucleus. In

a quantum-mechanical treatment, the classical description of the interaction is no

longer strictly possible. However, one can introduce the concept of the eﬀective

interaction distance, at which the radiation loss process is aﬀected by the electronic

Coulomb ﬁeld. This distance is of the order of ~/q, where q is the recoil momen-

tum of the atom after the interaction took place. If ~/q is large compared with the

atomic radius, the screening eﬀect has to be taken into account.

Under the Born approximation (see [Bethe and Heitler (1934); Heitler (1954);

Bethe and Ashkin (1953)]), Bethe and Heitler derived a quantum-mechanical calcu-

lation of the bremsstrahlung emission by an electron in the ﬁeld of a heavy, pointlike

and spinless nucleus. They determined the atomic radius from the Thomas–Fermi

model, where it is expressed as

1/3

in which a

is the Bohr radius (see Appendix A.2). For an electron with incident

energy E

, the maximum frequency ν

of the emitted photon is given by

hν

= E

− mc

After emitting a photon, for an electron with ﬁnal energy

E = E

− hν

the eﬀect of screening can b e evaluated by the screening parameter η:

η = 100

hν

1/3

. (2.92)

η is essentially the radius of the atom divided by the maximum possible value of ~/q

allowed by the energy and momentum conservation in the interaction. For η À 1

the screening eﬀect can be neglected, while for η ' 0 the screening is complete.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 97

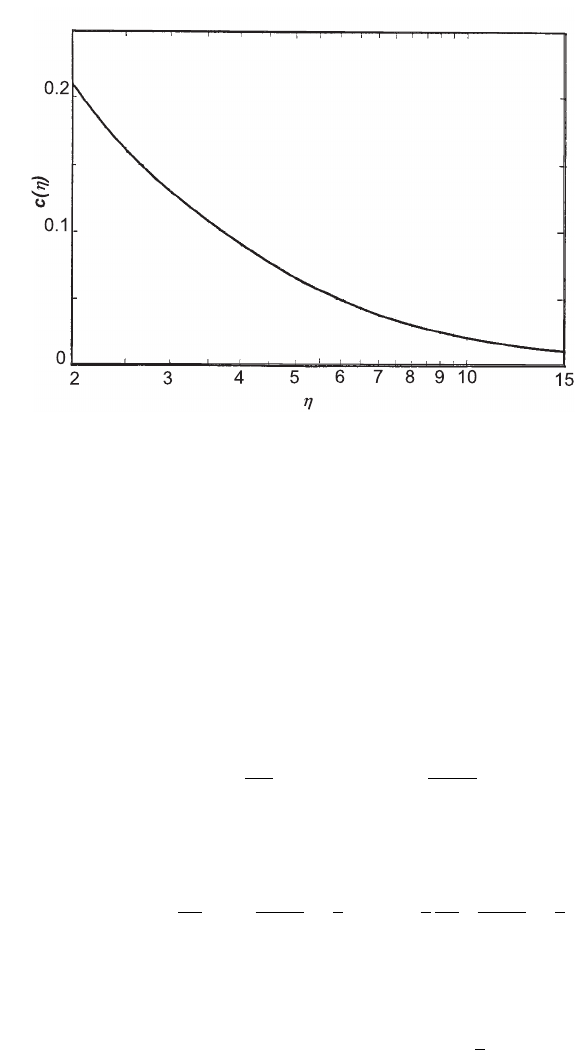
Fig. 2.28 Screening function c(η) versus η (adapted and reprinted with permission from [Bethe

and Ashkin (1953)], see also [Bethe and Heitler (1934)]).

In the framework of Bethe and Heitler’s calculations for the interaction in a

nuclear ﬁeld, the probability that an electron with incoming energy E

traversing

a thickness x in cm emits a photon with energy between hν and hν + d(hν) is:

Φ(E

, hν) dx d(hν),

where Φ(E

, hν) d(hν) is in units of cm

−1

. In this section, all equations referring

to Φ(E

, hν) d(hν) are expressed in cm

−1

. Φ(E

, hν) is called diﬀerential radiation

probability, for which we have

Φ(E

, hν) d(hν) = 4 α

Nρ

F (E

, hν, η)

d(hν)

hν

[cm

−1

], (2.93)

where, for E

large compared with mc

, the function F(E

, hν, η) depends on the

screening parameter η:

F (E

, hν, η) =

1 +

(η)

−

ln Z

−

(η)

−

ln Z

The functions ϕ

(η) and ϕ

(η) are shown in Fig. 2.27 for 0 < η < 2.

For η ≈ 0 (i.e., for complete screening) we have

(0) = 4 ln 183 and ϕ

(0) = 4 ln 183 −

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

98 Principles of Radiation Interaction in Matter and Detection

and Eq. (2.93) becomes:

Φ(E

, hν) d(hν)

= 4 α

Nρ

F (E

, hν, 0)

d(hν)

hν

= 4 α

Nρ

4 ln 183

−

ln Z

−

4 ln 183 −

−

ln Z

)

d(hν)

hν

= 4 α

Nρ

1 +

−

183

1/3

)

d(hν)

hν

. (2.94)

For larger η values, the eﬀect of screening decreases and, for η > 2, we have

(η) = ϕ

(η) = ϕ(η),

with

ϕ(η)

−

ln Z = ln

hν

−

− c(η)

and

ϕ(η) = 4 ln

hν

ln Z − 2 − 4 c(η), (2.95)

where the function c(η) is shown in Fig. 2.28. The diﬀerential radiation probability

becomes:

Φ(E

, hν) d(hν)

= 4 α

Nρ

F (E

, hν, η > 2)

d(hν)

hν

= 4 α

Nρ

−

hν

−

−c(η)

)

d(hν)

hν

. (2.96)

For η À 1 (i.e., for no screening), c(η) becomes negligible and Eq. (2.96)

becomes:

Φ(E

, hν) d(hν)

= 4 α

Nρ

1 +

−

hν

−

)

d(hν)

hν

. (2.97)

The equations for the diﬀerential radiation probability were derived assuming

that the Born approximation can be used. However, the Born approximation gives

correct results [Heitler (1954)] only if

2πZe

¿ 1 and

2πZe

¿ 1,

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 99

where v and v

are the electron velocities after and before photon emission, respec-

tively. Because α = e

/(~c), for electrons moving at speeds v and v

close to c, the

Born approximation is satisﬁed for:

2πZα ≈ 4.6 × 10

−2

Z ¿ 1.

As a consequence, some corrections are needed for high-Z materials, and also for

electrons at very high energies (see discussion in [Heitler (1954)]): for the high-

Z elements, corrections between (5–9)% are expected. Experimental data [Bethe

and Ashkin (1953)] indeed indicate a larger radiation emission in a Ta target. The

correction is expected to be proportional to (αZ)

The above equations were derived taking into account the nuclear ﬁeld

alone. However (see [Bethe and Ashkin (1953)] and references therein), the radiation

emission in the ﬁeld of atomic electrons can contribute to the overall radiation loss

process. This contribution is of the order of 1/Z of the nuclear contribution. If the

energy is large compared with mc

, but small enough for neglecting the screening

eﬀect, Eq. (2.97) is still valid for electrons, just Z has to be replaced by 1 (the

atomic electron charge). In this way (i.e., for no screening), Eq. (2.97) gives the

diﬀerential probability of the photon emission for both nuclear and atomic-electron

ﬁelds, when we replace Z

by Z(Z + 1):

e−n

, hν) d(hν) = 4 α

Nρ

Z(Z + 1) r

1 +

−

hν

−

d(hν)

hν

[cm

−1

]. (2.98)

In the limit of complete screening (η ' 0), Wheeler and Lamb (1939) derived

that the overall electron contribution to the diﬀerential radiation probability per

unit length is:

, hν) d(hν) = 4 α

Nρ

1 +

−

1440

2/3

)

d(hν)

hν

[cm

−1

]. (2.99)

The term E/(9E

) is small and can b e neglected in calculating the ratio

††

ι:

ι =

ZΦ

, hν)

Φ(E

, hν)

≈

1440/Z

2/3

183/Z

1/3

The ratio ι is 1.40, 1.29 and 1.14 for Z = 1, 10 and 92, respectively. For complete

screening, the overall diﬀerential radiation probability becomes:

e−n

, hν) d(hν) = 4 α

Nρ

Z(Z + ι) r

1 +

−

183

1/3

)

d(hν)

hν

[cm

−1

]. (2.100)

††

This ratio expresses Z times the electron contribution over the nuclear contribution computed

by means of Eq. (2.94).