Leroy C., Rancoita P.-G. Principles Of Radiation Interaction In Matter And Detection

Подождите немного. Документ загружается.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

110 Principles of Radiation Interaction in Matter and Detection

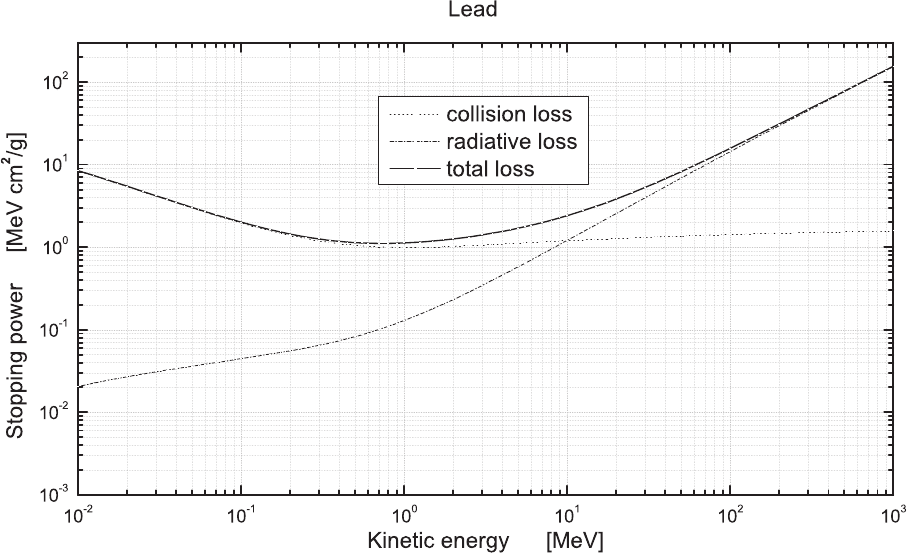
Fig. 2.36 Total, collision and radiation stopping powers in units of MeV cm

/g as a function of the incoming electron kinetic energy in units of

MeV in W (data from [Berger, Coursey, Zucker and Chang (2005)]).

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 111

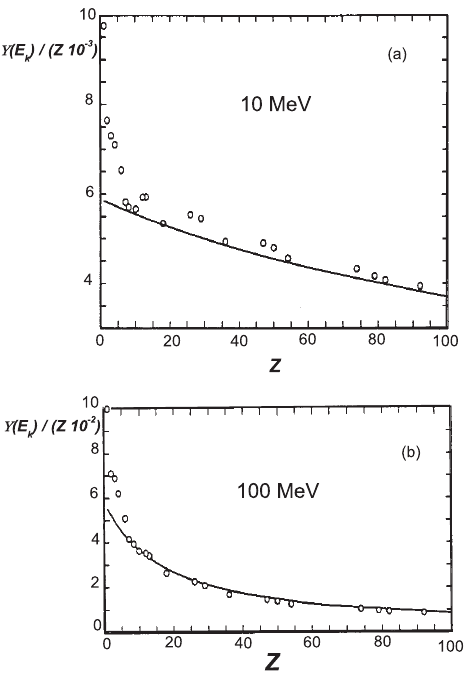
Fig. 2.37 Total, collision and radiation stopping powers in units of MeV cm

/g as a function of the incoming electron kinetic energy in units of

MeV in Pb (data from [Berger, Coursey, Zucker and Chang (2005)]).

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

112 Principles of Radiation Interaction in Matter and Detection

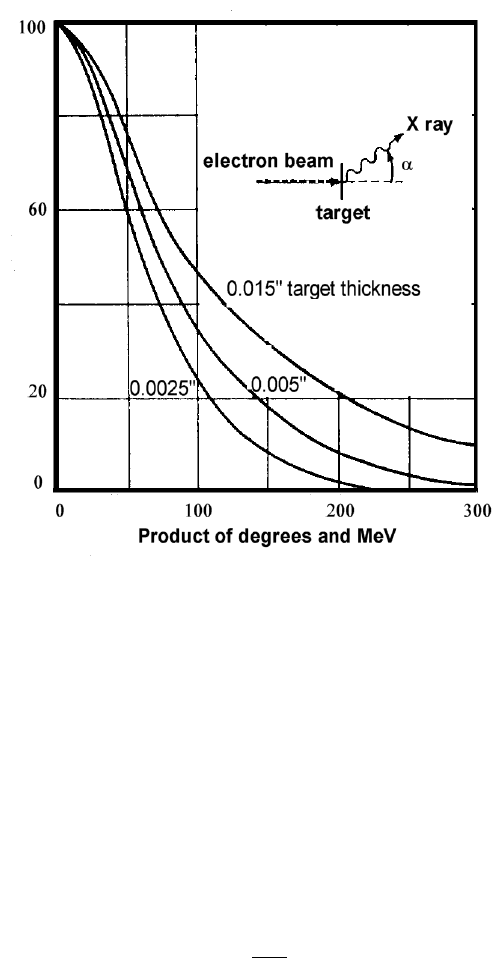
Fig. 2.38 Radiation yield Υ(E

) as a function of the atomic number Z calculated for a continuous

slowing-down process (adapted and reprinted with permission from [Berger and Seltzer (1964)]):

(a) Υ(E

)/(Z 10

−3

) for electron kinetic energy of 10 MeV, (b) Υ(E

)/(Z 10

−2

) for electron kinetic

energy of 100 MeV. The curve represents the Koch and Motz formula [Eq. (2.112)].

where τ = E

/mc

. This formula seems adequate for all materials except for those

with very low Z: for Z = 1 it underestimates the yield value by a factor ' 2, but

it becomes valid for Z larger than 6 (see Fig. 2.38).

At non-relativistic energies, no analytical or empirical formulae are available to

estimate the bremsstrahlung angular distribution for thick targets in which there are

additional relevant processes contributing to the overall energy decrease. However,

there are some experimental results [Koch and Motz (1959)].

At relativistic energies, estimates of the bremsstrahlung angular distributions

were made. These calculations agree fairly well with experimental data as those

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 113

Fig. 2.39 Predictions for the angular distribution for thick target bremsstrahlung of electrons in

tungsten with three diﬀerent thicknesses: 0.0025”, 0.005” and 0.015” (adapted and republished

with permission from Koch, H.W. and Motz, J.W., Rev. Mod. Phys. 31, 920 (1959); Copyright

(1959) by the American Physical Society, see also references therein). The abscissa is the product

of the electron kinetic energy in MeV and the angle in degrees: αE

[degree MeV]. The ordinate

is the percentage of the radiated intensity R

normalized to the radiated intensity at 0

◦

. R

deﬁned as the fraction of the total incident electron kinetic energy that is radiated per steradian

at angle α.

shown in Fig. 2.39 regarding electrons through tungsten ([Koch and Motz (1959)]

and references therein). Analytical expressions for the bremsstrahlung angular di-

stributions at diﬀerent electron energies and references to experimental data are

given in [Koch and Motz (1959)].

Most of the photons coming from a high-energy electron are emitted at relatively

small angles. The average emission angle θ

is given by:

, (2.113)

where E

is the incoming electron energy. The emission cone becomes more and

more narrow as the energy increases. In addition, bremsstrahlung photons are, in

general, polarized with the polarization vector normal to the plane formed by the

photon and incident electron [Segre (1977)].

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

114 Principles of Radiation Interaction in Matter and Detection

Table 2.6 Values of the functions L

rad

and L

rad

used to

compute the radiation length by means of Eq. (2.118) (see

Table B.2 in [Tsai (1974)]).

Element Z L

rad

H 1 5.31 6.144

He 2 4.79 5.621

Li 2 4.74 5.805

Be 3 4.71 5.924

others > 4 ln

184.15 Z

−1/3

1194 Z

−2/3

2.1.7.3 Radiation Length and Complete Screening Approximation

Electrons and positrons traversing a medium lose energy by radiation, as described

in previous sections. It is convenient to introduce a quantity, called radiation length,

to measure the distance traveled while radiative processes occur. The radiation

length is the distance over which the electron has reduced its energy by a factor e

and it is denoted by X

(in units of cm) or by X

g 0

(in units of g/cm

At suﬃciently high energy, i.e., when the radiative emission is the dominant

energy-loss process and the screening parameter η [deﬁned by Eq. (2.92)] approaches

0, the total radiation cross section is that for complete screening except in the case

of high frequency emitted photons [see Eqs. (2.105, 2.110)]. This cross section does

not depend on the incoming electron energy E

. For the case of complete screening

in the Born approximation, let us introduce the quantity

183

1/3

¢¤

[cm], (2.114)

where n

= N ρ/A is the number of atoms per cm

and the term

5.8 ×10

−28

×αZ(Z + ι) [cm

]. In addition,

is proportional to the total radiation

cross section Φ

rad

, i.e., from Eq. (2.105) we have:

= Φ

rad

Á·

4 ln

183

1/3

In this latter expression, the fraction 2/9 can be neglected with respect to the loga-

rithmic term. Thus, Eq. (2.114) for the radiation length X

can be ﬁnally rewritten

as:

≈

rad

[cm].

In order to understand the physical meaning of the above-deﬁned radiation

length, let us introduce the parameter

18 ln

183

1/3

. (2.115)

The reader can see Eq. (2.106) and the values of ι given in Sect. 2.1.7.

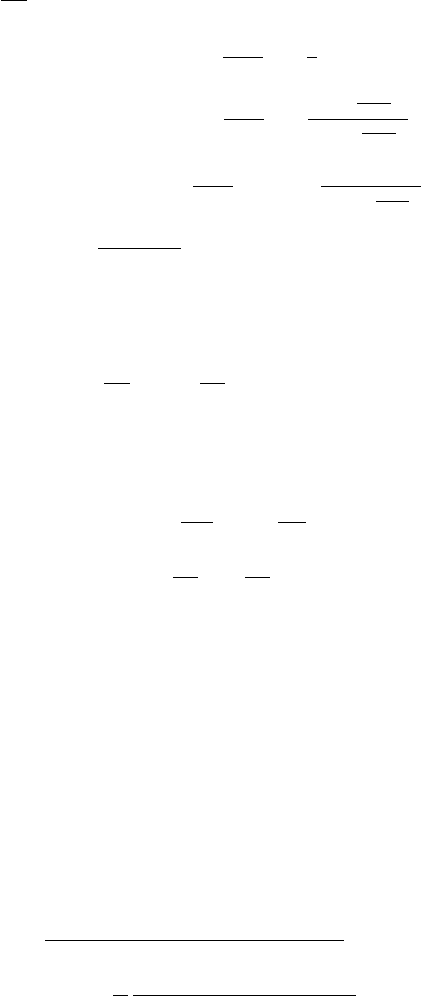
January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 115

Introducing Eqs. (2.105, 2.114, 2.115), for any given initial energy E in units of

MeV, Eq. (2.101) can be rewritten as:

−

rad

= n

EΦ

rad

= En

4 ln

183

1/3

= En

4 ln

183

1/3

4 ln

183

1/3

18 ln

183

1/3

= 4n

183

1/3

1 +

18 ln

183

1/3

E(1 + b

)

[MeV/cm].

The parameter b

is ' 0.012 for air and ' 0.015 for Pb (Z = 82); as a consequence,

it can be neglected. Furthermore, X

is independent of the energy E

. Thus, we can

write:

−

rad

[MeV/cm]. (2.116)

After traversing a thickness x of matter, the ﬁnal energy E

of an electron of

incoming energy E can be calculated by integrating the previous equation. We

obtain:

−

⇒ ln

−

from which, ﬁnally, we get

= E e

(−x/X

)

. (2.117)

While the meaning of the radiation length is outlined in Eq. (2.117), the actual

value depends on the assumptions under which the total radiation cross section

is treated. For instance, as described above, Eq. (2.114) is valid when the Born

approximation can be employed [Bethe and Ashkin (1953)]. Other authors derived

slightly modiﬁed expressions for the radiation length (see [Rossi (1964); Dovzhenko

and Pomamskii (1964)]).

A comprehensive treatment of the radiation length was derived by Tsai (1974);

it includes the eﬀects due to atomic and nuclear form factors for light and heavy

elements. The complete expression for the radiation length is given by

4 n

αr

rad

− g(Z)] + L

rad

}

= 716.405

rad

− g(Z)] + L

rad

}

[cm], (2.118)

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

116 Principles of Radiation Interaction in Matter and Detection

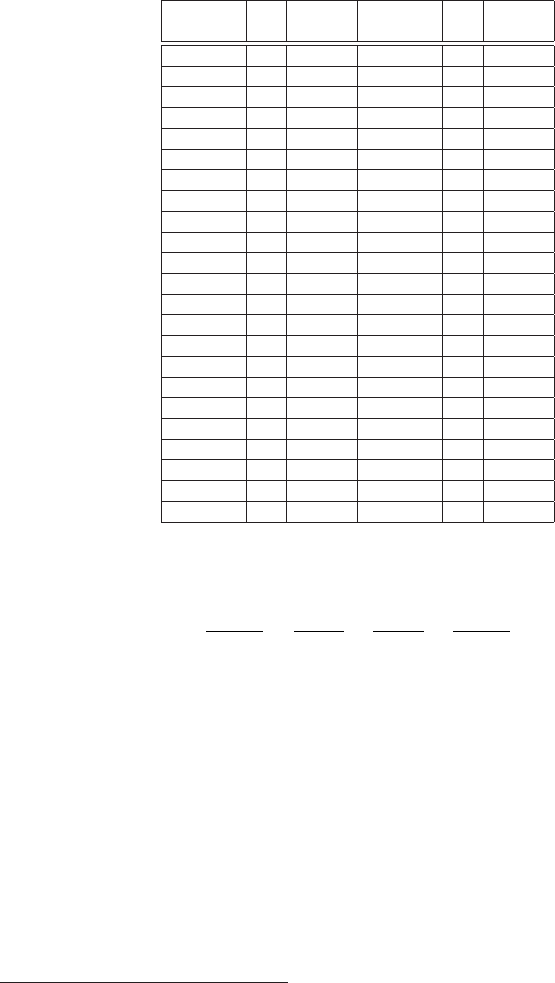
Table 2.7 Values of the radiation lengths X

in units

of g/cm

from Eq. (2.118) (see [Tsai (1974)]), and

atomic number Z for elements with Z up to 46.

Element Z X

g/cm

H 1 63.05 Cr 24 14.94

He 2 94.32 Mn 25 14.64

Li 3 82.76 Fe 26 13.84

Be 4 65.19 Co 27 13.62

B 5 52.69 Ni 28 12.68

C 6 42.70 Cu 29 12.86

N 7 37.99 Zn 30 12.43

O 8 34.24 Ga 31 12.47

F 9 32.93 Ge 32 12.25

Ne 10 28.94 As 33 11.94

Na 11 27.74 Se 34 11.91

Mg 12 25.04 Br 35 11.42

Al 13 24.01 Kr 36 11.37

Si 14 21.82 Rb 37 11.03

P 15 21.02 Sr 38 10.76

S 16 19.50 Y 39 10.41

Cl 17 19.28 Zr 40 10.19

Ar 18 19.55 Nb 41 9.92

K 19 17.32 Mo 42 9.80

Ca 20 16.14 Tc 43 9.69

Sc 21 16.55 Ru 44 9.48

Ti 22 16.18 Rh 45 9.27

Va 23 15.84 Pd 46 9.20

where the functions L

rad

and L

rad

are shown in Table 2.6; g(Z) is the Coulomb

correction approximated by [Tsai (1974)]:

g(Z) ≈ 1.202 (αZ)

− 1.0369 (αZ)

+ 1.008

(αZ)

1 + (αZ)

The radiation length values

‡

, X

= X

ρ, are given in Tables 2.7 and 2.8 in units

of g/cm

. The radiation lengths X

g0,c

of chemical compounds and mixtures of

molecules (such as air) can be calculated using the mass fraction F

of elements

and the radiation lengths X

g o,i

of each element shown in Tables 2.7 and 2.8:

g0,c

g 0 ,i

. (2.119)

The corresponding density ρ

(in g/cm

) can be calculated from:

, (2.120)

where ρ

(in g/cm

) is the density of the ith absorber. For instance, assuming that

air consists of 76.9% of nitrogen (Z = 7), 21.8% of oxygen (Z = 8) and 1.3% of

‡

They were computed by means of Eq. (2.118).

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 117

Table 2.8 Values of the radiation lengths X

in units

of g/cm

from Eq. (2.118) (see [Tsai (1974)]), and

atomic number Z for elements with Z from 47 up to

92.

Element Z X

g/cm

Ag 47 8.97 Yb 70 7.02

Cd 48 8.99 Lu 71 6.92

In 49 8.85 Hf 72 6.89

Sn 50 8.82 Ta 73 6.82

Sb 51 8.72 W 74 6.76

Te 52 8.83 Re 75 6.69

I 53 8.48 Os 76 6.67

Xe 54 8.48 Ir 77 6.59

Cs 55 8.31 Pt 78 6.54

Ba 56 8.31 Au 79 6.46

La 57 8.14 Hg 80 6.44

Ce 58 7.96 Tl 81 6.42

Pr 59 7.76 Pb 82 6.37

Nd 60 7.71 Bi 83 6.29

Pm 61 7.52 Po 84 6.19

Sm 62 7.57 At 85 6.07

Eu 63 7.44 Rn 86 6.29

Gd 64 7.48 Fr 87 6.19

Tb 65 7.37 Ra 88 6.15

Dy 66 7.32 Ac 89 6.06

Ho 67 7.23 Th 90 6.07

Er 68 7.14 Pa 91 5.93

Tm 69 7.03 U 92 6.00

argon (Z = 18) by weight, we have

g 0 ,air

0.769

g 0 ,N

0.218

g0, O

0.013

g 0 ,Ar

from which we ﬁnd X

g 0 ,air

= 36.66 g/cm

2.1.7.4 Critical Energy

As discussed in previous sections, electrons and positrons undergo both radiative

and collision energy-losses. The former is proportional to the particle energy [see

Eq. (2.116)], while the latter depends logarithmically on it [see Eq. (2.78)]. Thus,

at high energies the dominant energy-loss process is by radiation emission. As the

electron energy decreases, the ionization and excitation collisions are more and more

important and, ﬁnally, becoming the dominant energy-loss process.

The critical energy ²

is the energy at which the electron

∗

loses an equal amount

of energy by radiation and collision. Bethe and Heitler (1934) gave a ﬁrst approxi-

∗

For muons, the values of the critical energy as function of the atomic number are reported in

Section 4.5 of [Groom, Mokhov and Striganov (2001)].

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

118 Principles of Radiation Interaction in Matter and Detection

mate formula; subsequently another expression was given by Amaldi (1981):

550

[MeV].

This expression is valid, within 10%, for absorbers with Z ≥ 13. An approximate

expression was also given by Berger and Seltzer (1964):

800

Z + 1.2

[MeV].

A more accurate formula for the critical energy is given by Dovzhenko and Pomam-

skii (1964):

= B

Z X

[MeV], (2.121)

where B = 2.66, and h = 1.11. This expression is normally employed for calculations

in this book. Values of the critical energy for several materials, calculated by means

of Eq. (2.121), are shown in Table 2.3.

It has to be noted that Rossi, treating the cascading shower transport inside

matter under the so-called “Approximation B” [Rossi (1964)], has indicated another

quantity as critical energy, i.e., the value of the electron energy at which the energy

loss by collision is given by the electron energy divided by the radiation length (see

also the discussion in Section 27.4.3 of [PDB (2008)]). The values of this parameter

are, within a few percent, close to the critical energies as deﬁned in this section.

2.2 Multiple and Extended Volume Coulomb Interactions

So far, we have considered phenomena related to the energy released electromag-

netically by charged particles traversing a medium. However, there are additional

Fig. 2.40 The multiple Coulomb scattering eﬀect on particles traversing a thickness L of material.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 119

eﬀects involving energy transfers small with respect to energy losses by collision

or by radiation. They occur at very reduced scale (i.e., for distances of approach

smaller than the atomic radius) or at very large scale, so that the medium po-

larization has to be taken into account. In this section, we describe the eﬀect of

the nuclear Coulomb elastic interaction resulting in the so-called multiple scattering

and relaxation eﬀects of polarized media via the emission of

Cerenkov radiation and

transition radiation.

2.2.1 The Multiple Coulomb Scattering

When a charged particle passes in the neighborhood of a nucleus, the most impor-

tant eﬀect is the deﬂection of its trajectory. Associated with the deﬂection, there are

photons emitted whose overall energy is usually very small with respect to that of

the incoming particle. Cases with large energy emissions are limited statistically. To

a ﬁrst approximation, we treat elastic Coulomb scatterings. In an elastic scattering,

the total-momentum conservation requires that the incident particle of charge ze

acquires an equal, but opposite transverse momentum with respect to the one ac-

quired [see Eq. (2.7)] by the recoil nucleus of charge Ze. This transferred momentum

is usually very small in comparison with the incoming particle momentum p. Thus,

the incoming particle is scattered at an angle θ given approximately by the ratio of

the transverse momentum to the total momentum p, i.e.,

θ ≈

2Zze

−1

2Zze

bvp

, (2.122)

where v is the particle velocity. From Eq. (2.122), the absolute value of the deﬂection

dθ at an angle θ is related to the impact parameter variation db at b by:

dθ =

2Zze

db. (2.123)

The probability of collision dP

of a particle traversing

a thickness dx with an

impact parameter between b and b + db is

= 2 n

πb db dx

= 2

Nρπ

b db dx,

and, by introducing Eq. (2.122) for b and Eq. (2.123) for db, dP

becomes

= 2

Nρπ

·µ

2Zze

−1

2Zze

−1

dθ

= 2

Nρπ

2Zze

dθ

dx,

In the traversed material, n

is the number of atoms with atomic weight A per cm

[Eq. (1.39)].