Leroy C., Rancoita P.-G. Principles Of Radiation Interaction In Matter And Detection

Подождите немного. Документ загружается.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

140 Principles of Radiation Interaction in Matter and Detection

Table 2.12 Energies of the absorption edges above 10 keV for ele-

ments with Z from 69 up to 100 from [Hubbell (1969)].

Element Z K-edge L

-edge L

III

-edge

keV keV keV keV

Tm 69 59.380 10.121

Yb 70 61.300 10.490

Lu 71 63.310 10.874 10.345

Hf 72 65.310 11.274 10.736

Ta 73 67.403 11.682 11.132

W 74 69.508 12.100 11.538 10.200

Re 75 71.658 12.530 11.954 10.531

Os 76 73.856 12.972 12.381 10.868

Ir 77 76.101 13.423 12.820 11.212

Pt 78 78.381 13.883 13.272 11.562

Au 79 80.720 14.354 13.736 11.921

Hg 80 83.109 14.842 14.212 12.286

Tl 81 85.533 15.343 14.699 12.660

Pb 82 88.005 15.855 15.205 13.041

Bi 83 90.534 16.376 15.719 13.426

Po 84 93.112 16.935 16.244 13.817

At 85 95.740 17.490 16.784 14.215

Rn 86 98.418 18.058 17.337 14.618

Fr 87 101.147 18.638 17.904 15.028

Ra 88 103.927 19.236 18.486 15.444

Ac 89 106.759 19.842 19.078 15.865

Th 90 109.646 20.464 19.683 16.299

Pa 91 112.581 21.102 20.311 16.731

U 92 115.620 21.771 20.945 17.165

Np 93 118.619 21.417 20.596 17.614

Pu 94 121.720 23.109 22.253 18.054

Am 95 124.876 23.793 22.944 18.525

Cm 96 128.088 24.503 23.640 18.990

Bk 97 131.357 25.230 24.352 19.461

Cf 98 134.683 25.971 25.080 19.938

E 99 138.067 26.729 25.824 20.422

Fm 100 141.510 27.503 26.584 20.912

section and the emitted-electron angular distribution can be obtained following

Heitler’s treatment (Chapter V, Section 21 in [Heitler (1954)]) and using the cor-

rections by Bethe and Ashkin (Section 3 in [Bethe and Ashkin (1953)]).

In the non-relativistic region

∗

, the Born approximation can be used for inco-

ming photon-energies large compared with the ionization energy of the K-shell elec-

trons. The angular distribution of the emitted electrons is expressed by the K-shell

diﬀerential cross section per atom:

dτ

k,B

dΩ

= 4

√

2 r

137

hν

7/2

sin

θ cos

(1 − β cos θ)

, (2.158)

where β is the velocity of the emitted electron in units of the speed of light, θ is the

angle between the directions of the incoming photon and the emitted electron, φ is

∗

This energy region is for hν ¿ mc

, where m is the rest mass of the electron.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 141

Table 2.13 Empirical-ﬁt parameters to K-shell photoelectric cross

section above 200 keV from [Hubbell (1969)].

n a

1 1.6268 × 10

−9

−2.683 × 10

−12

4.173 × 10

−2

2 1.5274 × 10

−9

−5.110 × 10

−13

1.027 × 10

−2

3 1.1330 × 10

−9

−2.177 × 10

−12

2.013 × 10

−2

3.5

4 −9.1200 × 10

−11

0 0 4

the angle between the scattering plane

†

and the direction of the incoming radiation

polarization (see Chapter V, Section 21 in [Heitler (1954)]). From Eq. (2.158), we

note that photoelectrons are mostly emitted along the polarization direction of the

incoming radiation (i.e., θ =

π and φ = 0). While along the incoming-photon

direction (i.e., θ = 0), the diﬀerential cross section goes to zero, i.e., no photoelec-

tron is emitted in the very forward direction. Furthermore [see the denominator

of Eq. (2.158)], although the photoelectrons can also be emitted in the backward

hemisphere (i.e., with emission angles larger than 90

◦

), they will be emitted more

and more in the forward hemisphere (i.e., with emission angles lower than 90

◦

) as

the photon energy increases. The K-shell total photoelectric cross section can be

derived from Eq. (2.158) by neglecting the term β cos θ in the denominator, then,

integrating over the full solid angle and, ﬁnally, multiplying the result by a factor

2 to account for two K-shell electrons; thus, we have:

k,B

= 2

dτ

k,B

dΩ

≈ 2

√

2 r

137

hν

7/2

sin

θ cos

φ dΩ

= σ

T h

√

137

hν

7/2

, (2.159)

where σ

T h

= (8/3)πr

(' 6.6516 × 10

−25

) is the classical Thomson scattering

cross section. For heavy elements or for incoming photon energies close to those

of absorption edges, the Born approximation is no longer valid and exact wave

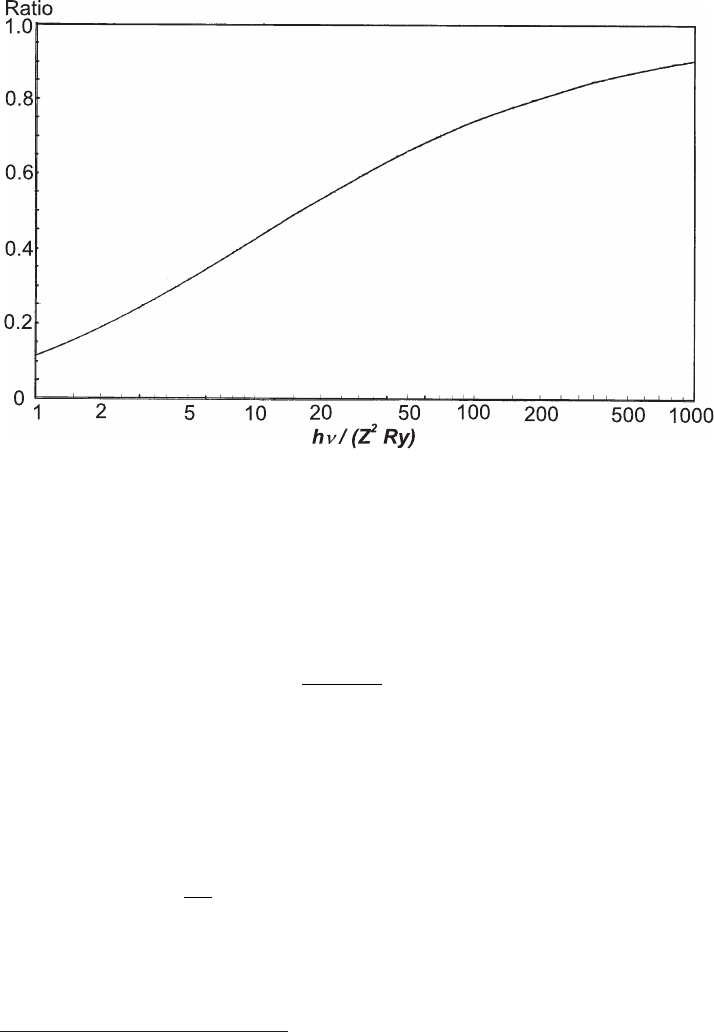
functions must be used. Figure 2.49 shows the ratio between the τ

values, calcu-

lated with exact wave functions, and those of τ

k,B

[Eq. (2.159)] as a function of

hν/(Z

Ry).

There are a few direct measurements of total and K-shell photoelectric cross

sections in the region between 100 keV and 3 MeV. However, most of the theoretical

information was derived for the K-shell component of the cross section (see [Hubbell

(1969)]). The extensive results by Rakavy and Ron (1965) include almost all the

higher shells and cover the range between 1 keV and 2 MeV. In the energy range

between 10 and 200 keV, the calculations [Rakavy and Ron (1965)] are in very good

agreement with the experimental data. The uncertainties on K-shell cross sections

†

It is the plane determined by the directions of the incoming photon and the emitted electron.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

142 Principles of Radiation Interaction in Matter and Detection

Fig. 2.49 Ratio τ

/τ

k,B

as a function of E

= hν/(Z

Ry) (adapted and reprinted with permission

from [Bethe and Ashkin (1953)]). τ

k,B

is calculated by means of Eq. (2.159).

are estimated to be about 2% in the region (0.2–100) MeV. Over the total photo-

electric cross section, the uncertainties are more likely to be about (3–5)% [Hubbell

(1969)]. Above 200 keV, an empirical formula for the K-shell photoelectric cross

section per atom is:

≈ Z

n=1

+ b

1 + c

−p

[b/atom], (2.160)

where E

is the incoming photon energy in MeV and the parameters a

, b

, c

and p

are given in Table 2.13.

To a ﬁrst approximation, for energies above K-shell binding energies, the total

photoelectric cross section τ

per atom can be obtained multiplying τ

by the

ratios

derived by Kirchner and Davisson [Kirchner et al. (1930)]. These ratios can

be computed, within an accuracy of ± (2–3)%, by the formula [Hubbell (1969)]:

≈ 1 + 0.01481 ln

Z − 0.000788 ln

Z. (2.161)

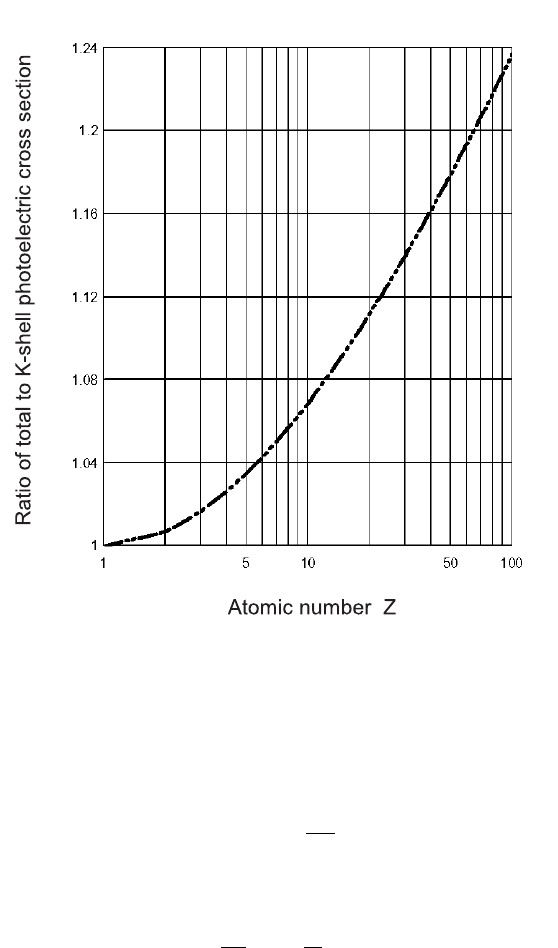
From Eq. (2.161), we note that, at large atomic numbers, the total photoelec-

tric cross section does not exceed the K-shell cross section by more than ≈ 25%

(Fig. 2.50). Other approximate empirical formulae

for photoelectric cross sections

can be found and are based on calculations made by Pratt (1960).

These ratios are assumed to be almost energy independent.

For instance, the reader can see Chapter 3, Section 7 in [Messel and Crawford (1970)].

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 143

Fig. 2.50 Ratio of the total over K-shell photoelectric cross section as a function of the atomic

number Z, from Eq. (2.161).

The contribution to the total linear attenuation coeﬃcient due to photoelectric

eﬀect is given by

att,l,ph

= n

ρN

[cm

−1

] (2.162)

with τ

in cm

/atom, while the total mass attenuation coeﬃcient due to photo-

electric eﬀect is:

att,m,ph

−1

]. (2.163)

For instance, let us estimate the photon attenuation coeﬃcients in Al absorber

at 20 keV incoming photon energy. At this energy, the photoelectric eﬀect is the

dominant absorption process in low-Z media. τ

k,B

[computed from Eq. (2.159)]

is ≈ 3.11 × 10

b/atom, while the ratio τ

/τ

k,B

is ≈ 0.4 for hν/(Z

Ry) ≈ 8.7

(Fig. 2.49). Thus, τ

is about 1.24 ×10

b/atom. Using Eq. (2.161), the ratio of the

total to the K-shell photoelectric cross section is estimated to be ≈ 1.09. Therefore,

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

144 Principles of Radiation Interaction in Matter and Detection

the total photoelectric cross section becomes approximately

≈ 1.09 τ

= 1.35 × 10

b/atom.

Finally, from Eqs. (2.162, 2.163) the linear and mass attenuation coeﬃcients are

≈ 8.1 cm

−1

and 3 g

−1

, respectively. Similarly, we can calculate the attenuation

coeﬃcients at 300 keV in Pb absorber. At this energy in Pb, the photon absorption

is almost due to the photoelectric interaction. τ

, computed by means of Eq. (2.160),

is about 0.86 × 10

b/atom. Therefore, from Eq. (2.161) the ratio of the total to

K-shell photoelectric cross section is estimated to be ≈ 1.22. Consequently, the total

photoelectric cross section becomes approximately

≈ 1.22 τ

= 1.05 × 10

b/atom.

From Eqs. (2.162, 2.163), the linear and mass attenuation coeﬃcients are ≈ 3.5 cm

−1

and 0.3 g

−1

, respectively.

Because the total photoelectric cross section depends on the atomic number Z

to a power close to 5, the photon absorption depends strongly on the medium for

photon energies for which the photoelectric process is dominant.

2.3.1.1 The Auger Eﬀect

As previously discussed, there are processes (like the photoelectric eﬀect) which

allow the emission of bound atomic electrons. However, when electrons are ejected

from an atomic shell, a vacancy is created in that shell leaving the atom in an

excited state. The atom with an electron vacancy in the innermost K-shell can

readjust itself to a more stable state by emitting one or more electrons instead of

radiating a single X-ray photon. This internal adjustment process is named after

the French physicist Pierre-Victor Auger, who discovered it in 1925 [Auger (1925)].

When an electron of the higher L-shell makes a transition to ﬁll a K-shell electron

vacancy, the available amount of energy is the diﬀerence between the K-shell and

L-shell binding energies: B

(K) − B

(L). This energy can be released via a photon

(radiative emission) or absorbed by a bound electron of an higher shell, causing its

ejection. This soft electron is called Auger electron.

The probability of non-radiative transition, with emission of Auger electrons,

is larger for low-Z material (see for instance experimental data in [Burhop (1955);

Krause (1979)]). The Auger yield decreases with the atomic number Z, and at

Z ≈ 30 the probabilities of X-rays emission from the innermost shell and of the

emission of Auger electrons are almost equal. An empirical formula [Burhop (1955)]

for the K-ﬂuorescence yield N

as a function of the atomic number is:

1 − N

= (−6.4 + 3.4Z −0.000103Z

)

× 10

−8

, (2.164)

where N

(the K-ﬂuorescence yield) is the probability for emitting photons per

K-shell vacancy, 1 − N

is the Auger yield (i.e., the probability for ejecting Auger

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 145

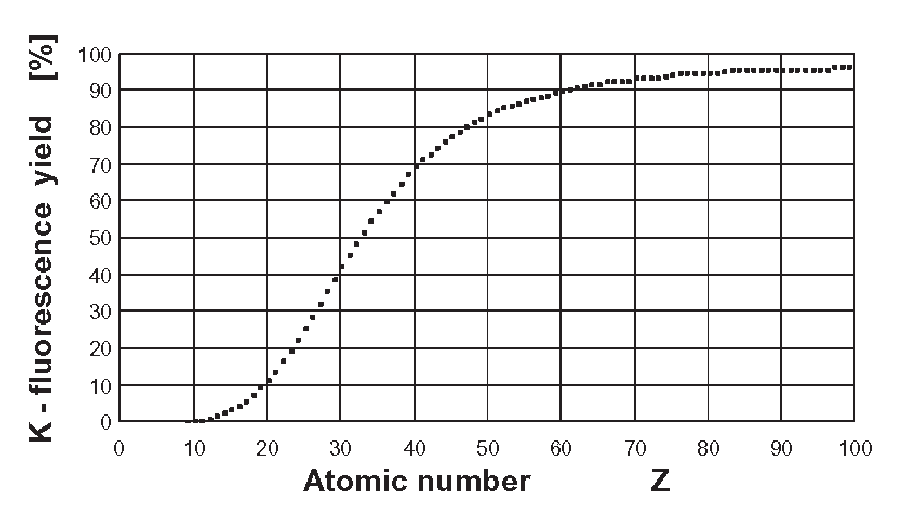
Fig. 2.51 Percentage of the K-ﬂuorescence yield N

computed by means of Eq. (2.165) as a function of the atomic number Z.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

146 Principles of Radiation Interaction in Matter and Detection

electrons per K-shell vacancy). From Eq. (2.164), we have:

= (1 − N

)(−6.4 + 3.4Z − 0.000103 Z

)

× 10

−8

(−6.4 + 3.4Z − 0.000103 Z

)

× 10

−8

1 + (−6.4 + 3.4Z − 0.000103 Z

)

× 10

−8

. (2.165)

as a function of Z is shown in Fig. 2.51.

2.3.2 The Compton Scattering

The Compton eﬀect is based on the corpuscular behavior of the incident radia-

tion and it is an incoherent scattering process on individual atomic electrons. These

electrons can be described as quasi-free, i.e., to a ﬁrst approximation their binding

energies do not aﬀect the interaction and can be neglected in calculations. Further-

more, it is considered as an inelastic process, although the kinematics description

of the reaction is that of an elastic collision.

The eﬀect was observed for the ﬁrst time by Compton (1922), who provided

a theoretical explanation, and it is depicted in Fig. 2.52. In the Compton eﬀect,

an incoming photon of momentum hν/c interacts with a (quasi-)free electron at

rest. The scattered photon emerges at an angle θ

with a momentum hν

/c, while

the electron recoils at an angle θ

with momentum ~p. By requiring momentum

conservation along the incoming photon direction, we have

hν

cos θ

+ p cos θ

from which we obtain

cos

= h

(ν − ν

cos θ

)

; (2.166)

Fig. 2.52 Compton scattering of an incident photon with incoming momentum hν/c onto a quasi-

free electron which emerges at an angle θ

. The photon is scattered at an angle θ

with a momentum

hν

/c.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 147

while in the perpendicular direction, we get:

hν

sin θ

= p sin θ

from which we ﬁnd

sin θ

= h

sin

. (2.167)

Due to energy conservation, we have

+ hν = hν

+ mc

+ K

, (2.168)

where m and K

are the mass and kinetic energy of the electron, respectively. Equa-

tion (2.168) can be written as:

= hν − hν

= h(ν −ν

). (2.169)

Furthermore, see Eq. (1.8), the total electron energy is given by:

+ K

+ m

⇒ m

+ K

+ 2mc

= p

+ m

from which we have

= K

+ 2mc

). (2.170)

By summing Eqs. (2.166, 2.167) and substituting p

with the value given by

Eq. (2.170), we obtain

+ 2mc

= h

(ν − ν

cos θ

)

+ ν

sin

= h

− 2νν

cos θ

+ ν

where we can substitute K

with the value obtained from Eq. (2.169):

(ν − ν

)

+ 2mc

h(ν − ν

) = h

− 2νν

cos θ

+ ν

⇒ h

− 2h

νν

+ h

+ 2mc

h(ν − ν

) = h

− 2h

νν

cos θ

+ h

and, ﬁnally, we get

h(ν − ν

) = h

νν

(1 − cos θ

) . (2.171)

By introducing the Compton wavelength of the electron

≡

, (2.172)

considering that the photon wavelength and frequency are related by νλ = c and,

ﬁnally, by dividing both terms by νν

, we can rewrite Eq. (2.171) as the so-called

Compton shift formula:

4λ ≡ λ

− λ = λ

(1 − cos θ

) . (2.173)

The quantity 4λ is called wavelength Compton shift. It increases as the photon

scattering angle θ

increases. The maximum wavelength shift occurs for θ

= 180

◦

i.e., for backward scattered photons for which 4λ = 2λ

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

148 Principles of Radiation Interaction in Matter and Detection

The scattered photon energy depends on the photon scattering angle θ

and it is

related to the incoming photon energy. The relationship can be derived by rewriting

Eq. (2.171) as:

hν = hν

νν

(1 − cos θ

) = hν

[1 + E (1 − cos θ

)] ,

where

E ≡

hν

is the reduced energy of the incoming photon. Thus, the fraction of the incoming

photon energy carried by the scattered photon is

hν

1 + E (1 − cos θ

)

, (2.174)

and, conversely, for the cosine of the photon scattering angle:

cos θ

= 1 −

hν

− 1

. (2.175)

From Eq. (2.174), for photons scattered in the forward direction, i.e., θ

→ 0

◦

, we

have hν

→ hν independently of the incoming photon energy hν. In addition, at

very low energies for which E ¿ 1, the energy of the scattered photon becomes

hν

≈ hν, independently of the scattering angle θ

. Under such circumstances, the

electron kinetic energy becomes negligible. From Eqs. (2.169, 2.174), the electron

kinetic energy can be rewritten as

= hν

E (1 − cos θ

)

1 + E (1 − cos θ

)

, (2.176)

or, equivalently, as a function of the recoil electron angle θ

= hν

2 E cos

(1 + E)

− E

cos

. (2.177)

The angles θ

and θ

are related by:

tan θ

1 + E

cot

. (2.178)

In soft collisions, the maximum electron recoil angle is θ

= 90

◦

and is reached when

the photon is scattered at angle θ

= 0

◦

, while for backward scattered photons, i.e.,

at the largest Compton shift [see Eq. (2.173)] where θ

→ 180

◦

, the recoiling electron

is emitted at angle θ

→ 0

◦

. From Eqs. (2.176, 2.177), we note that, for backward

scattered photons, the electron kinetic energy reaches its maximum value:

e,m

= hν

2 E

1 + 2 E

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 149

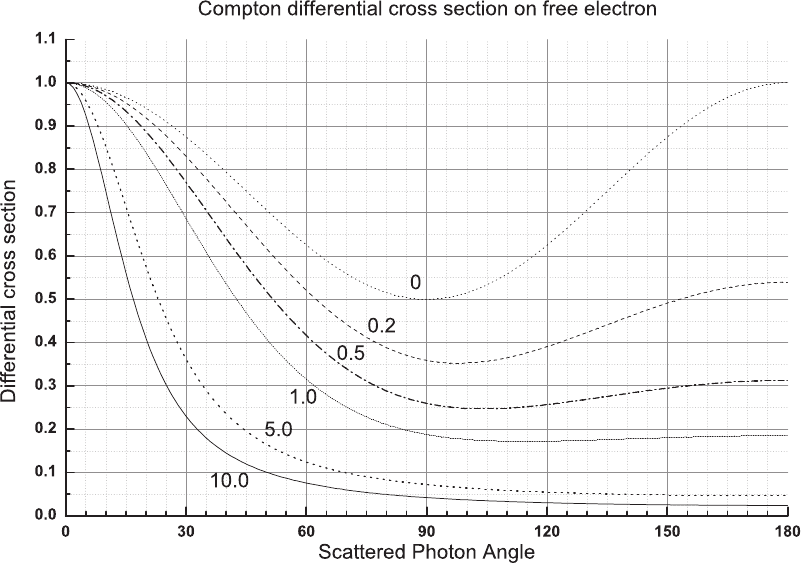
Fig. 2.53 Compton diﬀerential cross section on free electrons in units of r

as a function of the scattered photon angle θ

, for reduced energies

E = 0, 0.2, 0.5, 1.0, 5.0, and 10. The curves were calculated by means of Eq. (2.180).