Leroy C., Rancoita P.-G. Principles Of Radiation Interaction In Matter And Detection
Подождите немного. Документ загружается.

January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
160 Principles of Radiation Interaction in Matter and Detection
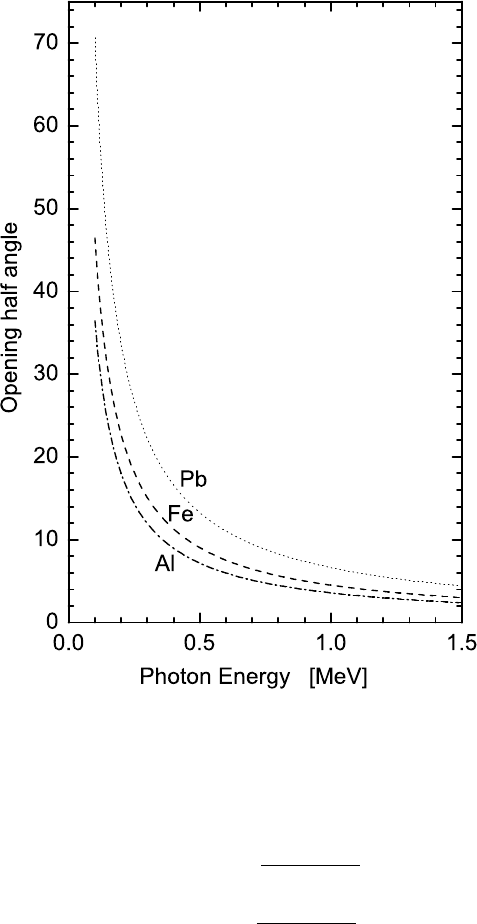
Fig. 2.59 Opening half angle in degrees as computed by means of Eq. (2.194) versus the photon
incoming energy in MeV for Al (bottom curve), Fe (mid curve) and Pb (top curve) absorbers.
criterion for determining the Rayleigh angular spread is [Moon (1950)]:
θ
R
= 2 arcsin
½
0.0133 Z
1/3
E[MeV]
¾
(2.194)
= 2 arcsin
·
0.0266 Z
1/3
E
¸
,
where θ
R
(in rad) is the opening half angle of a cone containing at least 75% of
the Rayleigh scattered photons. Figure 2.59 shows θ
R
as a function of the photon
incoming energy in Al, Fe and Pb absorbers.
The inclusion of both binding energy corrections to free electron Compton inte-
raction (i.e., the Compton interaction as treated in the Klein–Nishina theory) and
January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
Electromagnetic Interaction of Radiation in Matter 161
Rayleigh scattering slightly enhances the total photon cross section. The percent-
age, by which the total cross section is increased, dep ends on the photon incoming
energy and on the atomic number. For instance, at 50 keV photon energy, it is ≈ 11,
6 and 8% for Al, Fe and Pb, respectively. These values become ≈ 6, 8 and 3% at
100 keV photon energy, and ≈ 3% for Pb and < 0.5% for Al and Fe at 1 MeV photon
energy. It has to be noted that, at these photons energies, the photoelectric effect
can either become dominant or give an important contribution to the total photon
cross section, depending on the atomic number of the material.
2.3.2.3 The Thomson Cross Section
We have seen that at low photon incoming energies, i.e., for E → 0, the differential
Compton cross section
∗
approaches the so-called classical Thomson differential cross
section. We have also seen at page 156 that, similarly, the total Compton cross
section on a free electron (as described in the Klein–Nishina Theory) for E → 0
approaches the total Thomson cross section. Therefore, the Thomson scattering
can be regarded as the high-wavelength limit of the Compton interaction.
Using a classical electrodynamic treatment to describe X-rays interaction in
matter, Thomson assumed that the incident radiation sets the quasi-free electron
into a forced resonant oscillation. The differential scattering cross section can be
introduced in classical electrodynamics (see for instance [Jackson (1975)]) as:
µ
dσ
dΩ
¶
T h
=
Radiated energy/unit of time/unit of solid angle
Incident energy flux in energy/unit of time/unit of area
.
The incident energy flux is the Poynting vector time-average for the incoming plane
wave, i.e.,
S
in
=
c
8π
E
2
i
erg cm
−2
s
−1
,
where
~
E
i
is the field amplitude of the plane wave. The energy flux, emitted at
an angle θ
ν
by an electric dipole set into a constant oscillation with a dipole field
strength, is given by S
o
=
c
4π
E
2
o
, where
~
E
o
is the dipole field strength at a distance
r. For an unpolarized incident wave with a field amplitude
~
E
i
, S
o
expressed in
erg cm
−2
s
−1
can be written as:
S
o
=
e
4
16 πm
2
c
3
r
2
E
2
i
(1 + cos
2
θ
ν
)
where m is the rest mass of the electron. Moreover, the energy per unit time passing
through an area dA normal to the direction of ~r and corresponding to a solid angle
dΩ = dA/r
2
is given by:
S
o
dA =
e
4
16πm
2
c
3
r
2
E
2
i
(1 + cos
2
θ
ν
)(r
2
dΩ)
=
e
4
16πm
2
c
3
E
2
i
(1 + cos
2
θ
ν
) dΩ.
∗
The reader can see Eq. (2.181) and the discussion at page 150.
January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
162 Principles of Radiation Interaction in Matter and Detection
Thus, the Thomson differential cross section [
¡
dσ
dΩ
¢
T h
in cm
2
sr
−1
/electron] becomes:
µ
dσ
dΩ
¶
T h
dΩ =
S
o
dA
S
in
=
£
e
4
/(16πm
2
c
3
)
¤
E
2
i
(1 + cos
2
θ
ν
)
[c/(8π)] E
2
i
dΩ
=
1
2
r
2
e
(1 + cos
2
θ
ν
) dΩ, (2.195)
where r
e
= e
2
/(mc
2
).
The total Thomson cross section can be calculated by integrating the differential
cross section [i.e., Eq. (2.195)] over the full solid angle:
σ
T h
=
Z
µ
dσ
dΩ
¶
T h
dΩ
=
1
2
r
2
e
Z
(1 + cos
2
θ
ν
) dΩ
= πr
2
e
Z
π
0
(1 + cos
2
θ
ν
) sin θ
ν
dθ
ν
=
8
3
π
µ
e
2
mc
2
¶
2
(2.196)
=
8
3
πr
2
e
[cm
2
/electron]. (2.197)
In the Thomson scattering, there is no energy dependent term and no change in
wavelength for the emitted radiation. The total Thomson cross section per atom
(
a
σ
T h
), assuming that independent interactions occur with each of the Z quasi-free
electrons in the atom, is given by:
a
σ
T h
= Zσ
T h
=
8
3
πr
2
e
Z [cm
2
/atom]. (2.198)
It has to be noted that the classical Thomson formula is valid only at low frequen-
cies, where quantum-mechanical effects can be neglected.
2.3.2.4 Radiative Corrections and Double Compton Effect
The Compton interaction, as described by the Klein–Nishina theory, has to be
extended both to the case in which the emission and the reabsorption of virtual
photons occurs (i.e., the so-called radiative correction of order α = 1/137) and to
the case in which an additional real photon (usually at low energy) is emitted (i.e.,
the so-called double Compton scattering). Calculations treating both effects can be
found for instance in [Mork (1971)]. Once these contributions are both added to
the Klein–Nishina cross section, but without taking into account either the electron
binding energy effect or the Rayleigh scattering, the total Compton cross section
on free electron becomes
σ
C
= σ
C,e
+ 4σ
C
, (2.199)

January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
Electromagnetic Interaction of Radiation in Matter 163
where 4σ
C
is the cross section variation due to b oth radiative corrections and the
double Compton effect, σ
C,e
is the Klein–Nishina cross section on free electron as
given by Eq. (2.187) or equivalently by Eq. (2.188). These corrections are negligible
for photons with energies below 100 keV, and amount to ≈ 0.25% and 1% of σ
C
at
4 and 100 MeV, respectively. At photon energies of ab out 1 GeV, 4σ
C
accounts for
≈ 5% of σ
C
.
The Compton attenuation coefficients have to be calculated including coherent
effects, i.e., those due to the Rayleigh scattering and to electron binding corrections
to the free electron cross section, as previously discussed (Sect. 2.3.2.2). However,
these effects do not mo dify the Compton cross section by more than a few percents
above ≈ 100 keV. In order to compute the linear and mass Compton attenuation
coefficients without coherence effects, we have to use the Compton cross section on
atom, which is Z times larger than the cross section σ
C
on an atomic electron. The
atomic cross section is given by Zσ
C
, where σ
C
is calculated using Eq. (2.199) and
the linear attenuation coefficient is given by:
µ
nocoh
att,l,C
= ρN
Z
A
σ
C
[cm
−1
].
The corresponding mass attenuation coefficient becomes
µ
nocoh
att,m,C
= N
Z
A
σ
C
[g
−1
cm
2
].
Furthermore, we can define the linear and mass attenuation coefficients related
to the corrected incoherent Compton cross section σ
incoh
, which accounts for the
electron binding corrections of the Z atomic electrons, the radiative corrections and
the double Compton effect. The corrected incoherent Compton cross section per
electron is
σ
incoh
= σ
B
C
+ 4σ
C
, (2.200)
where σ
B
C
is given by Eq. (2.191).
It has to be noted that Z/A is ≈ 0.4–0.5, above Z = 1. Thus, the Compton mass
attenuation coefficient is almost independent of the medium above ≈ 100 keV (see
also page 159).
2.3.3 Pair Production
As the incoming photon energy exceeds twice the energy corresponding to the elec-
tron rest mass, i.e., 2mc
2
' 1.02 MeV, the production of an electron and positron
pair becomes possible (see Fig. 2.60). The process of pair production can only oc-
cur close to a charged massive object (for instance a nucleus) which takes away
the amount of momentum needed to preserve momentum conservation, during
the interaction with the Coulomb field of the massive object itself. Furthermore,
in the framework of the Dirac theory, this process is intimately related to the
bremsstrahlung process.
January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
164 Principles of Radiation Interaction in Matter and Detection
The photon threshold energy, E
γ,th
, depends on the mass of the particle, whose
Coulomb field allows the pair production process to happen. The value of E
γ,th
needed to create an electron and positron pair of mass 2m can be computed con-
sidering that, for a target of mass M at rest in the laboratory system, the minimal
final invariant mass is M
1,2
= M + 2m. From Eq. (1.33), we have
M
2
1,2
= M
2
+
2
c
4
(E
γ,th
Mc
2
) = M
2
+ 4mM + 4m
2
,
from which we obtain:
E
γ,th
= 2mc
2
³
1 +
m
M
´
. (2.201)
Therefore, when the pair production occurs in the proximity of a nucleus the thresh-
old energy is E
γ,th
' 2m, while in proximity of an electron E
γ,th
' 4m. In addition
to the different threshold energy, the pair production in the field of a nucleus exhi-
bits two observable tracks in tracking detectors. Three tracks can be observed for
the pair production in the electron field, because of the presence of the fast recoiling
electron. The pair production in the field of an electron is sometime referred to as
the triplet production.
The pair production process becomes the dominant mechanism for photon inte-
ractions in matter above E ≈ 10 and accounts for almost the whole γ-ray absorption
in this energy range.
2.3.3.1 Pair Production in the Field of a Nucleus
The quantum-mechanical treatment of pair production in the electron field can
be simplified using the Born approximation, as derived by Heitler (1954) (see also
references therein), and applies for:
2πZe
2
~v
±
=
2πZα
β
±
¿ 1,
where α = e
2
/(~c) is the fine structure constant and v
+
, v
−
are the velocities of the
positron and electron, respectively.
Similarly to what was discussed in Sect. 2.1.7 regarding the bremsstrahlung
emission, the probability of pair creation depends on the effective distance between
the incoming photon and the nucleus. The screening can be neglected if energies of
both positron and electron are not too high, i.e., if
2αZ
1/3
E
+
E
−
E(mc
2
)
¿ 1, (2.202)
where E
+
, E
−
are the total energies of the positron and electron, respectively, and
E is the incoming photon energy.
The effective distance from the nucleus determines the extent to which the elec-
tric field of the nucleus is screened by outer electrons. The influence of screening is
given by the quantity η, the so-called screening parameter:
η = 100
mc
2
E
1
f
+
(1 − f
+
)
Z
−1/3
, (2.203)
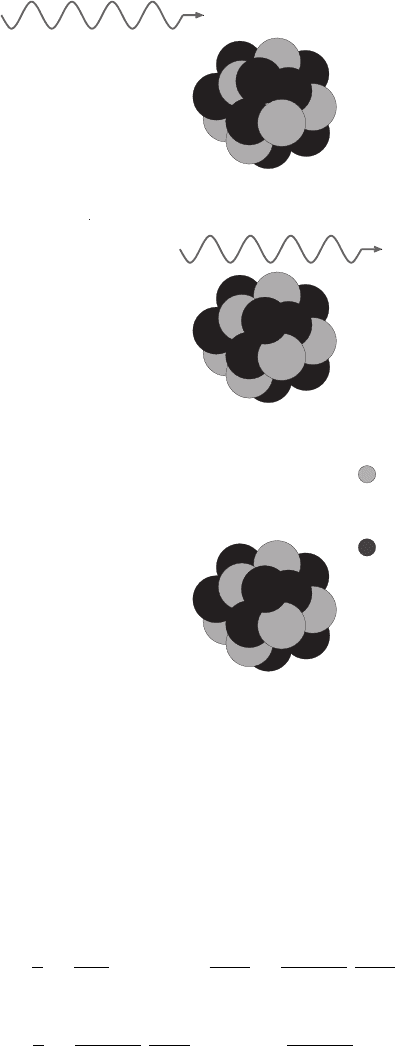
January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
Electromagnetic Interaction of Radiation in Matter 165
e
e
+
−
γ
γ
Fig. 2.60 An incoming photon interacts with the Coulomb field of a massive nucleus. Finally, an
electron and positron pair emerges.
where f
+
and (1 − f
+
) = f
−
are the fractional energies carried by the positron
and the electron, respectively: f
+
= E
+
/E, f
−
= E
−
/E. As already mentioned,
the nuclear recoil preserves momentum conservation. In addition, to a first appro-
ximation, we have E
+
+ E
−
= E. Thus, the positron energy, as well as the electron
energy, varies between mc
2
and E − mc
2
. Let us now rewrite Eq. (2.203) for the
parameter η as
1
η
=
E
mc
2
f
+
(1 − f
+
)
Z
1/3
100
=
E
+
E
−
E(mc
2
)
Z
1/3
100
,
and, when the screening is negligible [Eq. (2.202)], we obtain:
1
η
=
E
+
E
−
E(mc
2
)
Z
1/3
100
< 2 αZ
1/3
E
+
E
−
E(mc
2
)
¿ 1.

January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
166 Principles of Radiation Interaction in Matter and Detection
Therefore, η is À 1 when screening is negligible.
Let us indicate with Φ
pair
(E, E
+
) dE
+
dx the probability that a positron (of
energy between E
+
and E
+
+ dE
+
) and electron pair is created by a photon of
energy E traversing an absorber of thickness dx. Here Φ
pair
(E, E
+
) is referred to
as the differential probability of pair production: Φ
pair
(E, E
+
) dE
+
is in units of
cm
−1
. For photon energies E À mc
2
, Φ
pair
(E, E
+
) can be written as ([Bethe and
Heitler (1934); Heitler (1954)] and references therein)
Φ
pair
(E, E
+
) dE
+
= 4α
Nρ
A
Z
2
r
2
e
P (E, E
+
, η)
dE
+
E
= 4
¯
Φ(Z)
pair
Nρ
A
P (E, E
+
, η)
dE
+
E
[cm
−1
], (2.204)
where
¯
Φ(Z)
pair
= αZ
2
r
2
e
' 5.8 × 10
−28
× Z
2
cm
2
and P (E, E
+
, η) depends on the
screening parameter η:
P (E, E
+
, η) =
E
2
+
+ E
2
−
E
2
·
ϕ
1
(η)
4
−
1
3
ln Z
¸
+
2
3
E
+
E
−
E
2
·
ϕ
2
(η)
4
−
1
3
ln Z
¸
. (2.205)
The functions ϕ
1
(η) and ϕ
2
(η) are shown in Fig. 2.27 for 0 ≤ η ≤ 2. Therefore,
the differential cross section dσ
pair
(E, E
+
, η)/dE
+
to create a p ositron (with energy
between E
+
and E
+
+ dE
+
) and an electron pair in the nuclear field is obtained
dividing the differential probability of pair production [e.g., Eq. (2.204)] by n
A
(= ρN/A), i.e., the number of atoms per cm
3
:
dσ
pair
dE
+
dE
+
=
1
n
A
Φ
pair
(E, E
+
) dE
+
= 4
¯
Φ(Z)
pair
P (E, E
+
, η)
dE
+
E
[cm
2
/atom], (2.206)
where E is the incoming photon energy.
For η ≈ 0, i.e., for complete screening, we have
ϕ
1
(0) = 4 ln 183 and ϕ
2
(0) = 4 ln 183 −
2
3
(see page 97); as a consequence, Eq. (2.204) becomes:
Φ
pair
(E, E
+
) dE
+
= 4
¯
Φ(Z)
pair
Nρ
A
P (E, E
+
, 0)
dE
+
E
= 4
¯
Φ(Z)
pair
Nρ
A
×
·µ
E
2
+
+ E
2
−
E
2
+
2
3
E
+
E
−
E
2
¶
ln
h
183 Z
−1/3
i
−
1
9
E
+
E
−
E
2
¸
dE
+
E
= 4
¯
Φ(Z)
pair
Nρ
A
×
½·
E
2
+
+ E
2
−
+
2
3
E
+
E
−
¸
ln
h
183 Z
−1/3
i
−
1
9
E
+
E
−
¾
dE
+
E
3
. (2.207)
January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
Electromagnetic Interaction of Radiation in Matter 167
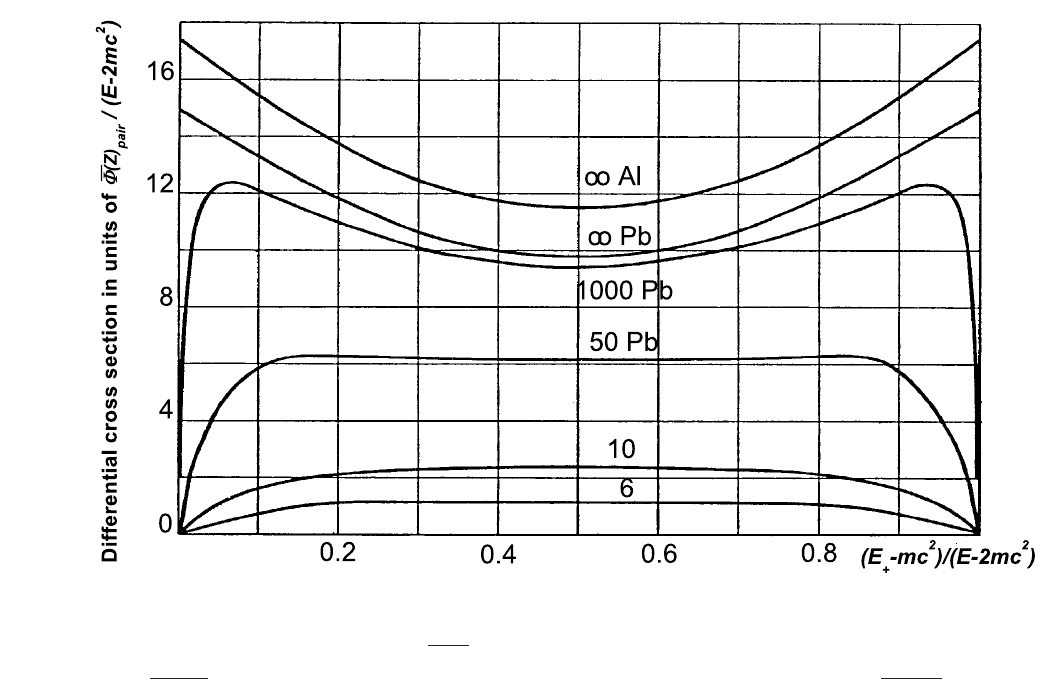
Fig. 2.61 Energy distribution of electron and positron pairs by means of Eq. (2.206), for reduced photon energies E of 6, 10, 50, 1000 and ∞ [Figure
16 (p. 261) from The Quantum Theory of Radiation 3rd Edition (1954) by Heitler, W., by permission of Oxford University Press], as calculated by
Heitler (1954). In ordinate, the differential cross section
dσ
pair
dE
+
for the creation of a positron with energy between E
+
and E
+
+ dE
+
[Eq. (2.206)]
is given in units of
¯
Φ(Z)
pair
E−2mc
2
. In abscissa, the kinetic energy of the positron is divided by the total kinetic energy, i.e.,
E
+
−mc
2
E−2mc
2
.
January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
168 Principles of Radiation Interaction in Matter and Detection
For larger values of η (i.e., for η > 2), the effect of screening decreases. We have
ϕ
1
(η) ' ϕ
2
(η) ' ϕ(η) (see page 98):
ϕ(η)
4
−
1
3
ln Z = ln
·
2E
+
E
−
Emc
2
¸
−
1
2
− c(η),
where the function c(η) is shown in Fig. 2.28 for 2 ≤ η ≤ 15. Hence, the differential
pair creation probability [Eq. (2.204)] in the nuclear field can be written as:
Φ
pair
(E, E
+
) dE
+
= 4
¯
Φ(Z)
pair
Nρ
A
P (E, E
+
, 2 ≤ η ≤ 15)
dE
+
E
= 4
¯
Φ(Z)
pair
Nρ
A
×
·
E
2
+
+ E
2
−
E
2
+
2
3
E
+
E
−
E
2
¸½
ln
·
2E
+
E
−
Emc
2
¸
−
1
2
− c(η)
¾
dE
+
E
= 4
¯
Φ(Z)
pair
Nρ
A
×
·
E
2
+
+ E
2
−
+
2
3
E
+
E
−
¸½
ln
·
2E
+
E
−
Emc
2
¸
−
1
2
− c(η)
¾
dE
+
E
3
. (2.208)
As η increases and becomes À 1, c(η) becomes negligible, i.e., ≈ 0. For no
screening, the differential pair creation probability [Eq. (2.204)] is given by:
Φ
pair
(E, E
+
)dE
+
= 4
¯
Φ(Z)
pair
Nρ
A
P (E, E
+
, η À 1)
dE
+
E
= 4
¯
Φ(Z)
pair
Nρ
A
×
·
E
2
+
+ E
2
−
+
2
3
E
+
E
−
¸½
ln
·
2E
+
E
−
Emc
2
¸
−
1
2
¾
dE
+
E
3
. (2.209)
The differential cross section, obtained by inserting in Eq. (2.206) the differential
probability given by Eq. (2.209), is valid for E À mc
2
and if the screening can
be neglected. The resulting equation is an approximate formula replacing the more
general Equation 8 given in Chapter V, Section 26 of [Heitler (1954)]. This latter
was derived under the condition that the screening can be neglected and its va-
lidity does not depend on the condition E À mc
2
. The energy distribution of the
pairs, dσ
pair
/dE
+
, is shown in Fig. 2.61. It was calculated by Heitler (1954) using
Eq. (2.206), as a function of the kinetic energy of the positron divided by the total
kinetic energy, i.e.,
E
+
−mc
2
E−2mc
2
. In the Fig. 2.61, the differential cross section is given
in units of
¯
Φ(Z)
pair
/(E − 2mc
2
). In ordinate, we have
·
dσ
pair
dE
+
¸·
E − 2mc
2
¯
Φ(Z)
pair
¸
.
Thus, the area under the curve is again related to the total cross section. The curves
are for reduced photon energies E of 6, 10, 50, 1000 and ∞ [Heitler (1954)]. The
January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
Electromagnetic Interaction of Radiation in Matter 169
calculations for small incoming energies (E = 6 and E = 10) are valid for any element
(the screening is neglected). The other curves are calculated for lead, and for E = ∞
in the case of lead and aluminum. It has to be noted that the screening is effective
if both the resulting electron and positron are with energies large compared with
mc
2
. Furthermore, at very high-energy, usually the screening is almost complete,
i.e.,
2
E
+
E
−
E(mc
2
)
À α
−1
Z
−1/3
.
Therefore, as it can be seen from Eq. (2.207), the energy distribution depends on
the atomic number Z. At low photon energies, the energy distribution shows a
broad flat maximum. On the contrary at very high energies, the curves show a
broad minimum for equal positron and electron energies, and a small maximum
when one of the particle receives the whole available energy. However, the nuclear
repulsion, if taken into account, should be favoring a slight asymmetry to produce
more high-energy positron.
Hough (1948a) provided a convenient approximate formula for the energy di-
stribution without screening for reduced photon energies 2 ≤ E ≤ 15, i.e., in units
of cm
2
/atom
dσ
pair
dE
+
dE
+
= z
H
µ
dσ
pair
dE
+
¶
m
dE
+
×
1+ 0.135
³
dσ
pair
dE
+
´
m
dE
+
¯
Φ(Z)
pair
− 0.52
z
H
(1 − z
2
H
)
, (2.210)
where
z
H
= 2
s
E
+
− mc
2
E − 2mc
2
µ
1 −
E
+
− mc
2
E − 2mc
2
¶
,
and
³
dσ
pair
dE
+
´
m
dE
+
is the value of the differential cross section for equal partition
of energy (E
+
= E
−
= E/2), which is obtained from Equation 8 in Chapter V,
Section 26 of [Heitler (1954)] and is approximated by [Hough (1948a)]:
µ
dσ
pair
dE
+
¶
m
dE
+
=
¯
Φ(Z)
pair
(1 − a
H
)
×
·
1
3
¡
4 − a
2
H
¢
(b
H
− 1) − a
2
H
c
H
(c
H
− 1) − a
4
H
c
H
(b
H
− c
H
)
¸
, (2.211)
where
a
H
=
2
E
b
H
=
·
2
(1 − a
2
H
)
¸
ln
E
2
c
H
=
1
p
1 − a
2
H
ln
E
2
+
s
µ
E
2
¶
2
− 1
.
