Leroy C., Rancoita P.-G. Principles Of Radiation Interaction In Matter And Detection
Подождите немного. Документ загружается.

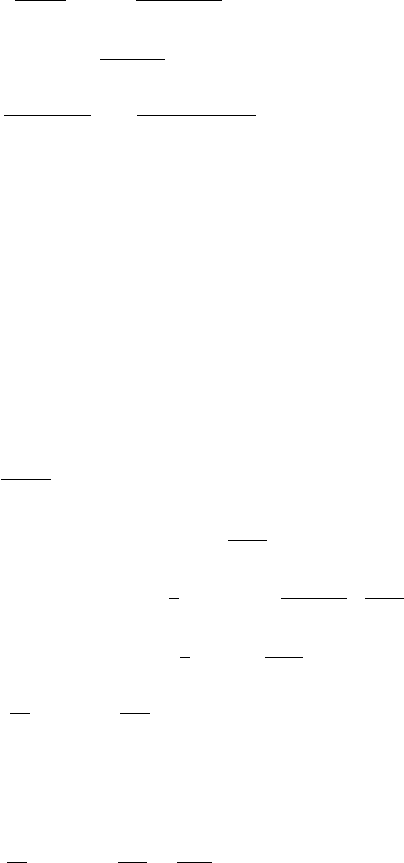
January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
170 Principles of Radiation Interaction in Matter and Detection
The second term in the bracket of Eq. (2.210) is to be dropped when it becomes
negative (below E ≈ 4.2). The differential cross section for equal partition of energy,
normalized to
¯
Φ(Z)
pair
and calculated using Eq. (2.211), is shown in Fig. 2.62 as a
function of the reduced photon energy E. While, the values of
·
dσ
pair
dE
+
dE
+
¸·
E − 2mc
2
¯
Φ(Z)
pair
¸
are shown in Fig. 2.63 as a function of
E
+
−mc
2
E−2mc
2
; as in Fig. 2.61, dE
+
is replaced by
d
µ
E
+
− mc
2
E − 2mc
2
¶
=
d
¡
E
+
− mc
2
¢
E − 2mc
2
.
Thus, the area under the curve is again related to the total cross section. For
the energy range 10 < E < 15, the differential cross section computed by means
of Eq. (2.210) is in overlap with the result obtained using Eq. (2.209). The most
suited approximate formulae for selected photon energies can be found in [Hough
(1948a)].
For photon energies such that
mc
2
¿ E ¿ α
−1
Z
−1/3
mc
2
,
the screening can be usually neglected. The total cross section for the pair pro-
duction in the nuclear field can be computed by taking into account Eq. (2.209)
and integrating under the condition E À mc
2
; one finds:
σ
pair,ns
=
Z
E−mc
2
mc
2
dσ
pair
dE
+
dE
+
=
Z
E−mc
2
mc
2
4
¯
Φ(Z)
pair
P (E, E
+
, η À 1)
dE
+
E
' 4
¯
Φ(Z)
pair
Z
E
mc
2
·
E
2
+
+ E
2
−
+
2
3
E
+
E
−
¸
ln
·
2E
+
E
−
Emc
2
¸
dE
+
E
3
−2
¯
Φ(Z)
pair
Z
E
0
·
E
2
+
+ E
2
−
+
2
3
E
+
E
−
¸
dE
+
E
3
=
¯
Φ(Z)
pair
·
28
9
ln(2 E) −
218
27
¸
[cm
2
/atom]. (2.212)
The result depends on the reduced photon energy E, but the term in bracket does not
depend on Z. However, Hough (1948a) has noted that Eq. (2.212) is not sufficiently
well approximated and a lower power of E must be added to the cross section:
σ
H
pair,ns
=
¯
Φ(Z)
pair
·
28
9
ln(2 E) −
218
27
+
6.45
E
¸
[cm
2
/atom]. (2.213)
For photon energies such that
E À α
−1
Z
−1/3
mc
2
(i.e. E À α
−1
Z
−1/3
),
January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
Electromagnetic Interaction of Radiation in Matter 171
Fig. 2.62 In ordinate
h³
dσ
pair
dE
+
´
m
dE
+
i
/
¯
Φ(Z)
pair
calculated using Eq. (2.211) as a function of the reduced photon energy E.

January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
172 Principles of Radiation Interaction in Matter and Detection
the screening is complete. For complete screening, the total cross section for
pair production in the nuclear field can be computed by means of Eq. (2.207) and
integrating under the condition E À mc
2
; one obtains:
σ
pair,cs
=
Z
E−mc
2
mc
2
dσ
pair
dE
+
dE
+
=
Z
E−mc
2
mc
2
4
¯
Φ(Z)
pair
P (E, E
+
, 0)
dE
+
E
' 4
¯
Φ(Z)
pair
×
Z
E
0
½·
E
2
+
+ E
2
−
+
2
3
E
+
E
−
¸
ln
³
183 Z
−1/3
´
−
1
9
E
+
E
−
¾
dE
+
E
3
=
¯
Φ(Z)
pair
·
28
9
ln
³
183 Z
−1/3
´
−
2
27
¸
[cm
2
/atom]. (2.214)
The result is independent of the photon energy, but the term in bracket depends
on Z.
The cross sections calculated by means of Eqs. (2.212, 2.213, 2.214) and divided
by
¯
Φ(Z)
pair
are shown in Fig. 2.64 for carbon and aluminum.
In general, deviations from the equations given in this section are ex-
pected. These formulae are less accurate for heavy elements, because they involve
the Born approximation. For instance, the Bethe–Maximon theory [Davies et al.
(1954)], which avoids the Born approximation, shows that the cross section for lead
is reduced by ≈ 12% at 88 MeV. Tsai (1974) has provided a detailed review on pair
production based on QED calculations and with atomic form factors taken into
account.
The cross section for pair production rises monotonically and varies approxi-
mately linearly with E until an almost constant value is reached above 50 MeV for
high-Z materials and at higher energies for low-Z absorbers.
A compilation of cross sections was given by White-Grodstein (1957). In the
energy region E < 5 MeV, where the screening can be neglected, cross sections were
calculated by means of Eq. (2.210) and treated with the inclusion of the Jaeger–
Hulme corrections [Jaeger and Hulme (1936)]. For E > 5 MeV, the corrections
involve Davies–Bethe–Maximon calculations [Davies, Bethe and Maximon (1954)]
and a semi-empirical formula in order to take into account the experimental data. A
later compilation made use of empirical corrections to cover the whole range from
threshold to high energy for the pair production cross section on the nuclear field
σ
pair,n
[Hubbell (1969)] (see also [Hubbell, Gimm and Øverbø (1980)]). This latter
is computed taking into account the Coulomb, screening and radiative corrections,
described below.
Disregarding screening and radiative corrections, the Coulomb interaction on the
nuclear field is described by an expression which gives rise to a perturbation series,
the first term of which is the Bethe–Heitler unscreened cross section (σ
B,ns
) in the
Born approximation. Under Maximon’s approximation [Maximon (1968); Hubbell
January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
Electromagnetic Interaction of Radiation in Matter 173
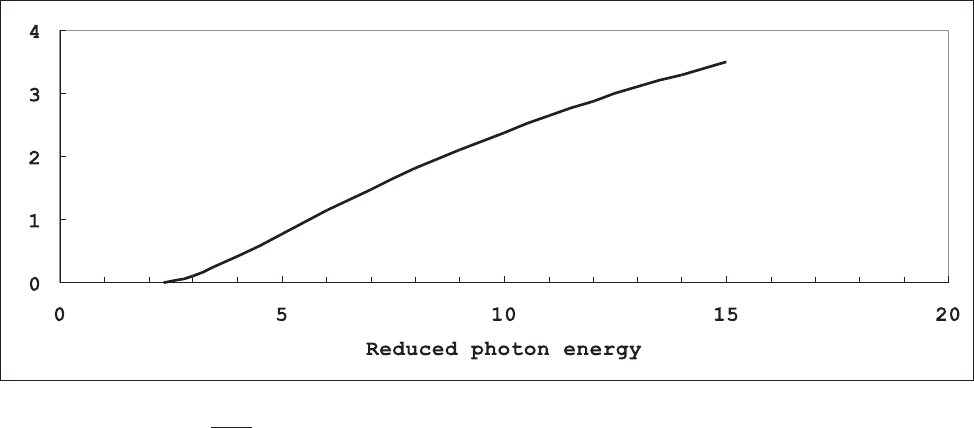
Fig. 2.63 Energy distribution of electron and positron pairs from Eq. (2.210) for the creation of a positron of energy between E
+
and E
+
+ dE
+
and for reduced photon energies E = 3, 6, 10, 12, and 15: in ordinate
h
dσ
pair
dE
+
dE
+
i
£¡
E − 2mc
2
¢
/
¯
Φ(Z)
pair
¤
is the normalized differential cross
section [i.e., the differential cross section divided by
¯
Φ(Z)
pair
/
¡
E − 2mc
2
¢
], in abscissa we have the kinetic energy of the positron divided by the
total kinetic energy, i.e.,
E
+
−mc
2
E−2mc
2
.

January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
174 Principles of Radiation Interaction in Matter and Detection
(1969)] σ
B,ns
(in units of cm
2
/atom) is given by
(a) for E ≤ 2 MeV:
σ
B,ns
¯
Φ(Z)
pair
=
2π
3
µ
E − 2
E
¶
3
µ
1 +
1
2
$ +
23
40
$
2
+
11
60
$
3
+
29
960
$
4
+ ···
¶
with
$ =
2 E − 4
2 + E + 2
√
2 E
,
(b) for E > 2 MeV:
σ
B,ns
¯
Φ(Z)
pair
=
28
9
ln(2 E) −
218
27
+
µ
2
E
¶
2
·
6 ln(2 E) −
7
2
+
2
3
ln
3
(2 E) − ln
2
(2 E) −
1
3
π
2
ln(2 E) + 2Z +
π
2
6
¸
−
µ
2
E
¶
4
·
3
16
ln(2 E) +
1
8
¸
−
µ
2
E
¶
6
·
29
9 × 256
ln(2 E) −
77
27 × 512
¸
+ ··· ,
where Riemann’s zeta-function is
Z =
X
n
1
n
2
= 1.2020569 . . . .
These two expansions for σ
B,ns
provide the unscreened cross section in the Born
approximation with values accurate within 0.01 percent over the whole range of
energies. Additional and detailed formulations can be found in Hubbell’s compila-
tion in [Hubbell, Gimm and Øverbø (1980)].
As already mentioned, if both screening and radiative corrections are not taken
into account for the Coulomb interaction, the first term of the perturbation series is
the Bethe–Heitler unscreened cross section (σ
B,ns
) in the Born approximation. The
sum of high order terms of this Born series determines the so-called Coulomb correc-
tion ∆
i
B
, where i depends on the approximation used for the calculation. For photon
energies ab ove 5 MeV, this term has to be subtracted from σ
B,ns
(see Equation 42
in Section 2.4 of [Hubbell, Gimm and Øverbø (1980)]).
The S¨orenssen expression for the Coulomb correction is given by ([S¨orenssen
(1965)] and references therein):
∆
S
B
= 4
¯
Φ(Z)
pair
f(Z)
µ
7
9
−
2
E
+
4
3 E
2
−
8
9 E
3
¶
[cm
2
/atom], (2.215)
with
f(Z) = a
2
B
·
1
(1 + a
2
B
)
+ 0.20206 − 0.0369a
2
B
+ 0.0083a
4
B
− 0.002a
6
B
+ ···
¸
and a
B
= αZ.

January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
Electromagnetic Interaction of Radiation in Matter 175
For large E values, Eq. (2.215) becomes the expression for the Coulomb correc-
tion as calculated by Davies–Bethe–Maximon (1954), i.e.,
∆
DBM
B
=
28
9
¯
Φ(Z)
pair
f(Z) [cm
2
/atom].
However, in particular for heavy elements, these corrections are not sufficiently
accurate for energies much lower than ≈ 100 MeV.
For low energies, exact calculations of the Coulomb correction were carried
out by Øverbø, Mork and Olsen (1968), who have provided a low energy un-
screened cross section σ
OM O
well adequate in the energy region ≤ 5 MeV. In ge-
neral, at energies lower than ≈ 100 MeV, the Coulomb correction was evaluated
by Øverbø [Øverbø, Mork and Olsen (1968); Øverbø (1977)] using an expression
containing the terms from Eq. (2.215):
∆
O
B
= ∆
S
B
−
¯
Φ(Z)
pair
E
·
0
1
ln
2
E
2
+ 0
2
ln
E
2
+ 0
3
µ
1 −
2
E
¶¸
−
¯
Φ(Z)
pair
E
2
·
0
4
ln
3
E
2
+ 0
5
ln
2
E
2
+ 0
6
µ
1 −
2
E
¶¸
[cm
2
/atom], (2.216)
where
0
1
= a
2
B
(−6.366 + 4.14 a
2
B
),
0
2
= a
2
B
(54.039 − 43.126 a
2
B
+ 11.264 a
4
B
),
0
3
= a
2
B
(−52.423 + 49.615 a
2
B
− 14.082 a
4
B
),
0
4
= 10.938 a
2
B
µ
1 −
a
2
B
0.324
¶
,
0
5
= −12.705 a
2
B
µ
1 −
a
2
B
0.324
¶
,
0
6
= 9.903 a
2
B
µ
1 −
a
2
B
0.324
¶
,
in which a
B
= αZ. Equation (2.216) contains the Davies–Bethe–Maximon correc-
tion as leading term. The largest error, occurring within the 5 to 50 MeV energy
region, is of the order of a few tenths of a % of the total cross section ([Hubbell,
Gimm and Øverbø (1980)] and references therein). However, for reduced energies
3.5 < E < 10, the errors are of the order of 0.1%.
An additional correction is that associated with the emission and reabsorption of
virtual photons and with the emission of both soft and hard photons. The numerical
values of the radiative correction were tabulated by Mork and Olsen (1965). At high
reduced energies, E > 1000, and for complete screening we have:
∆
rad.corr
= (0.93 ± 0.05) % .
For the cross section, the radiative correction is given by the multiplicative term
(1 + ∆
rad.corr
) (see Equation 42 in Section 2.4 of [Hubbell, Gimm and Øverbø
(1980)]).

January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
176 Principles of Radiation Interaction in Matter and Detection
The screened cross section (σ
B,s
) in the Born approximation was worked out in
the high-energy approximation by Bethe and Heitler (1934). We indicate by ∆
B,scr
the difference between the unscreened cross section σ
B,ns
and the screened cross
section σ
B,s
. However, Tseng and Pratt (1972) demonstrated that the screening
correction ∆
B,scr
is not adequately described in the Born approximation at low
energy; in addition, they provided a table for the screening correction for E < 10. A
more complete set of screening corrections, also valid at higher energies, is given by
Øverbø (1979) and it is discussed in detail in [Hubbell, Gimm and Øverbø (1980)].
2.3.3.2 Pair Production in the Electron Field
As in the case of bremsstrahlung, the pair production can occur in the Coulomb
field of atomic electrons. The recoiling electron can receive a sufficient amount of
momentum to emerge as an additional (to the produced positron and electron pair)
fast-electron from the interaction. As previously mentioned, this phenomenon is
referred to as the triplet production, due to three emerging fast-particles.
To a first approximation (see [Bethe and Ashkin (1953)] and references therein),
the distribution of recoil momenta, q, of the atomic electron is almost the same as
it would be for the nucleus if the pair were produced in the nuclear field. The recoil
momentum distribution is given by [Bethe and Ashkin (1953)]
P (q) dq =
1
A
q
mc
2
mc
2
+ q
2
dq
q
,
provided that q > q
min
, where
A
q
= ln
µ
mc
q
min
¶
and q
min
is the largest between
q
min
=
mc
E
or q
min
= mc
Z
1/3
183
.
The momentum distribution is almost uniform in a logarithmic scale. Thus, many
recoiling electrons have low energies.
The theory without screening correction is based on Borsellino–Ghizzetti’s calcu-
lations of [Borsellino (1947)] (see also [Hubbell (1969); Hubbell, Gimm and Øverbø
(1980)] and references therein). Ghizzetti’s expansion (here shown up to the first
leading term) gives the cross section, σ
BG
e
, for pair production in the field of an
atomic electron without screening:
σ
BG
e
=
¯
Φ(Z)
pair
Z
2
·
28
9
ln(2 E) −
218
27
−
1
E
B(E)
¸
[cm
2
/electron], (2.217)
where the function B(E) is given by
B(E) =
4
3
ln
3
(2 E) − 3 ln
2
(2 E) + 6.84 ln(2 E) − 21.51.
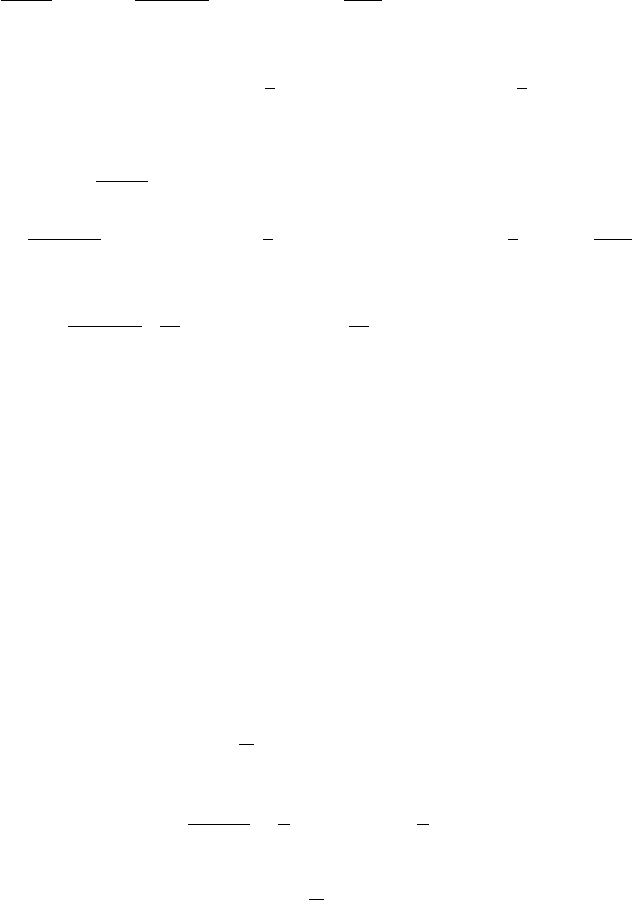
January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
Electromagnetic Interaction of Radiation in Matter 177
For large values of E, the term 1/E can be neglected and the term in brackets of
Eq. (2.217) becomes identical to the corresponding term of Eq. (2.212).
For photon energies larger than ≈ 20 MeV, the effect of screening cannot be
neglected anymore. Wheeler and Lamb (1939) gave the following expression in the
limit of complete screening for the differential cross section for pair production
in the field of an atomic electron:
dσ
W L
pair
dE
+
dE
+
= 4
¯
Φ(Z)
pair
Z
2
W(E
+
, E
−
, Z)
dE
+
E
3
[cm
2
/electron], (2.218)
where the function W(E
+
, E
−
, Z) is given by
W(E
+
, E
−
, Z) =
·
E
2
+
+ E
2
−
+
2
3
E
+
E
−
¸
ln
³
1440 Z
−1/3
´
−
1
9
E
+
E
−
.
This equation, once integrated, provides the total cross section per electron:
σ
W L
pair
=
Z
E−mc
2
mc
2
dσ
W L
pair
dE
+
dE
+
' 4
¯
Φ(Z)
pair
Z
2
Z
E
0
½·
E
2
+
+ E
2
−
+
2
3
E
+
E
−
¸
ln
³
1440 Z
−1/3
´
−
1
9
E
+
E
−
¾
dE
+
E
3
,
from which we obtain, finally,
σ
W L
pair
=
¯
Φ(Z)
pair
Z
2
·
28
9
ln
³
1440 Z
−1/3
´
−
2
27
¸
[cm
2
/electron]. (2.219)
The result is independent of the photon energy, but the term in brackets depends
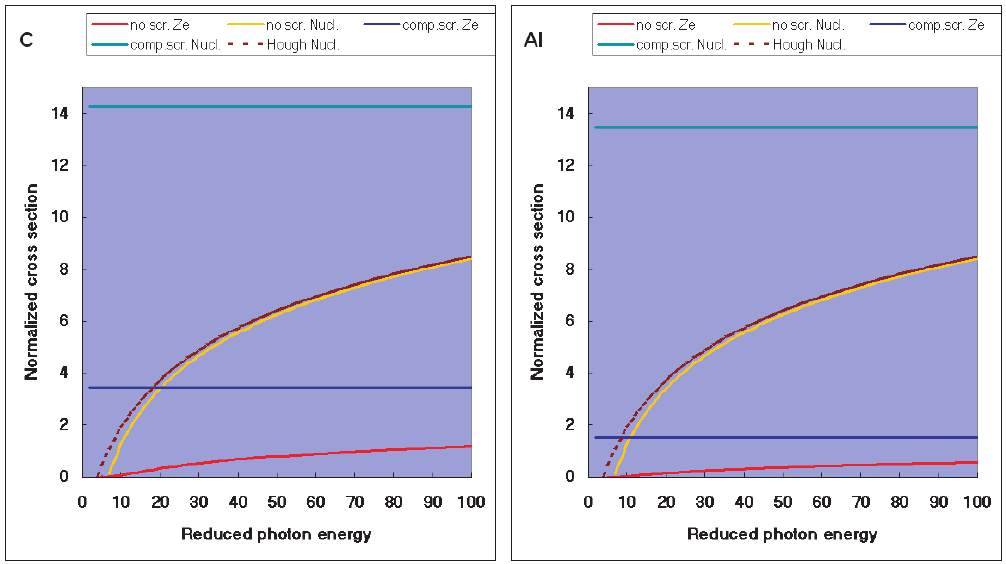
on Z, similarly to Eq. (2.214). For instance, Fig. 2.64 shows the cross sections
[divided by
¯
Φ(Z)
pair
] for pair production in the field of atomic electrons in carbon
and aluminum; these cross sections were computed by means of Eq. (2.217) for no
screening and Eq. (2.219) for complete screening, and multiplied by 6 (or 13) to
take into account the electrons available in carbon (or in aluminum).
Furthermore, to compute the total cross section for pair production σ
pair,e
in
an atomic field, the theoretical treatment must include effects like i) the atomic
binding of the target electron, ii) the screening by other atomic electrons and by
the nuclear field, iii) the virtual Compton scattering in which the scattered photon
(on the atomic electron) generates an electron–positron pair and, also, iv) radiative
corrections. In an empirical way and within ≈ 5%, σ
pair,e
can be written in terms
of the cross section for pair production in the nuclear field σ
pair,n
(see page 172)
as [Hubbell (1969)]
σ
pair,e
=
ς
Z
σ
pair,n
[cm
2
/atom],
where ς is given by:
ς =
3 + αZ
9
ln
E
2
− 0.00635 ln
3
E
2
.
The total atomic cross section for pair production becomes:
σ
pair,tot
= σ
pair,n
+ σ
pair,e
=
³
1 +
ς
Z
´
σ
pair,n
[cm
2
/atom]. (2.220)
January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
178 Principles of Radiation Interaction in Matter and Detection
Fig. 2.64 Pair production cross sections divided by
¯
Φ(Z)
pair
(in ordinate) for carbon(C) and aluminum (Al) as a function of the reduced photon
energy E. The asymptotic nuclear pair production cross section without screening is calculated using Eqs. (2.212, 2.213), with screening using
Eq. (2.214). For pair production in the atomic electron field, the curves are obtained by means of Eq. (2.217) for no screening and Eq. (2.219) for
complete screening [once multiplied by 6 (or 13) to take into account the available electrons in C (or in Al)].

January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
Electromagnetic Interaction of Radiation in Matter 179
A detailed discussion of triplet production can be found in [Hubbell, Gimm and
Øverbø (1980)] (see also references therein).
Furthermore, it has to be noted that the linear and mass attenuation co-
efficients accounting for the pair production effect can be computed using
Eqs. (2.155, 2.156, 2.220).
2.3.3.3 Angular Distribution of Electron and Positron Pairs
At high energy, pairs are mostly emitted in the forward direction, similarly to the
photon emission in the case of the bremsstrahlung effect. The average angle θ
p
bet-
ween the electron- (p ositron-) motion direction and the incoming-photon direction
is of the order of
θ
p
≈
mc
2
E
.
The angular distribution at small angles is given by [Hough (1948b)]
P (θ
p
) dθ
p
=
1
8
µ
mc
2
E
1
¶
2
E
2
1
+ E
2
2
E
2
1
+
2
3
E
1
E
2
+ E
2
cos
2
θ
p
2
sin
4
θ
p
2
sin θ
p
dθ
p
, (2.221)
where E
1
is the energy of one electron in the pair and E
2
is the energy of the second
electron. The probability to produce electrons at angles larger than an angle θ
g
can
be obtained by integrating Eq. (2.221) over the emission angle:
P (θ
p
> θ
g
) =
Z
π
θ
g
P (θ
p
) dθ
p
=
1
8
µ
mc
2
E
1
¶
2
1
1 − cos θ
g
.
2.3.4 Photonuclear Scattering, Absorption and Production
The photon scattering by the Coulomb nuclear field has more theoretical impli-
cations than practical ones. Nuclear Thomson and resonance scatterings, as well
as nuclear photo electric and Delbr¨uck scattering cross sections, are smaller than
the cross section of the main photon interaction mechanisms discussed so far. In
this section, A is the notation for the mass number (see discussion at page 220 in
Sect. 3.1).
The elastic scattering of photons by nuclear Coulomb fields may occur not only
via Thomson scattering, whose cross section can be calculated by replacing i) the
charge e by Ze (where Z is the atomic number) and ii) the target electron mass
m by the nuclear mass in the formula given by Eq. (2.196), but also through the
Delbr¨uck scattering. The latter scattering occurs via the virtual or real creation of
an e
+
e
−
pair, which subsequently annihilates.
The photonuclear absorption most likely results in the emission of a neutron,
but charged particles, γ-rays or more than a single neutron can also be ejected. For
photon energies below the threshold for nucleon removal, i.e., typically 7–8 MeV,
