Leroy C., Rancoita P.-G. Principles Of Radiation Interaction In Matter And Detection

Подождите немного. Документ загружается.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

200 Principles of Radiation Interaction in Matter and Detection

energy, from the ﬂow of the generated shower particles, is lost and eventually de-

posited in matter via excitation and ionization of atoms. The incoming energies

considered are À mc

αZ

1/3

. Therefore, radiation phenomena and pair produc-

tion can be described by asymptotic formulae for complete screening, while the

Compton eﬀect is neglected. In what is called “Approximation B”, collision losses

of electrons are taken into account. However, the energy-dependent collision-loss is

replaced by a constant collision-loss occurring in a radiation length called critical

energy ²

. It is taken, for ²

, the energy lost (by collisions in a radiation length)

by electrons of energy equal to the critical energy itself. No diﬀerence is considered

between electrons and positrons. This deﬁnition of ²

diﬀers from that one intro-

duced in Sect. 2.1.7.4, but typically its values are in agreement within a few percent

with those ones computed by means of Eq. (2.121) used in the present Sect. 2.4

and in the chapter on Principles of Particle Energy Determination. The assump-

tion of constant energy-loss for electrons derives from the fact that in all substances

the critical energy is larger than η

and for energies above η

the collision loss is

slowly varying with the incoming electron energy (see Sect. 2.1.7.1 and, for instance,

Figs. 2.33–2.37). The assumption of similar energy-loss for electrons and positrons

can be justiﬁed by considering that electron and positron collision losses do not

diﬀer by more than a few % over a wide range of energy (see Sect. 2.1.6.1). It has

also to b e noted that for β ≈ 1 (β = v/c, where v is the velocity of the particle

and c the speed of light) the collision losses by electrons are ≈ 10% larger than the

collision losses by heavy particles, and that the ratio ²

is approximately 10%

larger than the collision losses for minimum ionizing particles (mip), which occurs

at β ≈ 0. 96.

The cascade process, leading to the propagation of the shower and energy dissi-

pation, is treated along the longitudinal direction and is described by means of a set

of linear integro-diﬀerential equations. Because of their formal similarity to equa-

tions occurring in the theory of diﬀusion phenomena, they are often referred to as

the diﬀusion equations. “Approximation B” yields identical results for all elements

provided thicknesses are measured in units of radiation length and energies in units

of critical energy. In “Approximation B”, the total track length, T , is the summed

length of all individual tracks of charged particles showering and dissipating their

energy in the calorimeter medium. It is given by

T =

], (2.227)

where E is the incoming particle energy. Equation (2.227) can be justiﬁed in the

following way: at high energies, pair production and bremsstrahlung processes allow

the cascade to develop. However, the energy absorption or dissipation in matter

mainly proceeds via collision losses at the constant rate per unit of length of ≈

. Therefore, the total path of cascade charged particles in the absorber will

be ≈ E

.³

. In reality, there exists a dependence of the total track length

on the minimal energy E

detectable by the calorimetric device [Crawford and

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 201

Messel (1962); Nagel (1965); Longo and Sestilli (1975); Amaldi (1981)]. Therefore,

the measurable track length T (ζ) is smaller than T and can be expressed [Amaldi

(1981)] as

T (ζ) = F (ζ)

], (2.228)

where

F (ζ) ∼ e

1 + ζ ln

1.526

¶¸

with

ζ = 4.58

and E

is the cut-oﬀ energy, namely the minimum kinetic energy of the electron

(positron) that can be detected in the calorimeter.

For a cascade shower, T [or T (ζ)] is proportional to the incident particle

energy. Thus, the resp onse of a calorimeter is proportional to the incident energy,

provided that it is proportional to the energy deposited by the particles of the

shower (i.e., in the absence of saturation eﬀects). Furthermore, the ﬂuctuations in

T [or T (ζ)] will determine the intrinsic energy resolution.

The multiplication of electrons and positrons occurs when their energy is much

larger than the critical energy and they get absorbed at lower energies, i.e., when

collision losses b ecome dominant. The number of charged particles and photons

increases rapidly with depth until the maximum, located at the depth t

max

of the

cascade, is reached, i.e., where the longitudinal development of the shower has a

maximum (also called shower maximum). This shower behavior can be understood

in a simpliﬁed way, following crude assumptions. Let E be the energy of an in-

coming photon, which at a depth ≈ 1 X

generates a pair of e

−

with equal

energies. After an additional distance of ≈ 1 X

both the electron and positron

will emit a bremsstrahlung photon. By continuing the pro cess and assuming equal

energy sharing among the generated particles, particles will double themselves every

radiation length. Thus, the number of particles at depth t is

N(t) ≈ 2

while their energy is

(t) ≈

N(t)

= 2

−t

When the particle energy is E

≈ ²

, the multiplication no longer continues. This

occurs at the maximum depth t

max

for which

max

) ≈ ²

≈ 2

−t

max

namely, t

max

≈ ln (E/²

). Under “Approximation B”, this maximum depth depends

on the incoming energy as ln

and is given by

max

= 1.01

− c

], (2.229)

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

202 Principles of Radiation Interaction in Matter and Detection

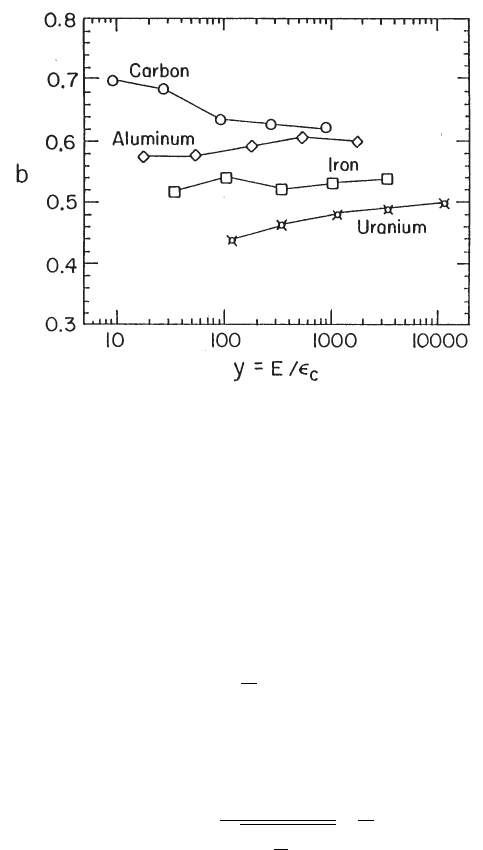
Fig. 2.76 Fitted values of the scale factor b for energy-deposition proﬁles obtained with the

simulation code EGS4 for incident electrons up to ≈ 100 GeV as function of y = E/²

(adapted

from Phys. Lett. B 592, Eidelman, S. et al., Review of Particle Physics, Edited by Particle Data

Group, 1–1109, Copyright (2004), with permission from Elsevier; see also [Leroy and Rancoita

(2000)]).

where c = 1.0 or 0.5 for incident electrons or photons, respectively. The location of

the shower center-of-gravity t

, i.e., the depth at which half of the incident energy

was deposited by the cascading particles (also indicated as the median depth of the

shower), is given by

= 1.01

+ d

], (2.230)

where d = 0.4 or 1.2 for incident electrons or photons, respectively. The number of

charged particles at t

max

is given by

max

) =







0.31

− e







, (2.231)

where e = 0.37 or 0.18 for incident electrons or photons, respectively.

2.4.2.2 Longitudinal Development of the Electromagnetic Shower

Simulation codes were written to reproduce the behavior of electromagnetic casca-

des in various media with the best possible accuracy [Nelson, Hirayama and Rogers

(1985)]. These codes attempted the inclusion, in a phenomenological way, of the

various eﬀects that the analytical approaches failed to describe. An example of such

an approach gives the average longitudinal development of cascades, i.e., the energy

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

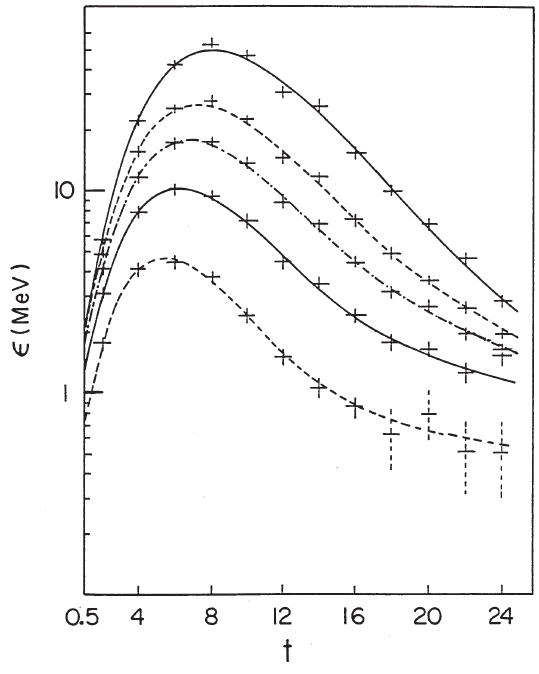
Electromagnetic Interaction of Radiation in Matter 203

Fig. 2.77 The electromagnetic-cascade longitudinal-development as a function of the calorimeter

depth (in units of radiation lengths) at 4, 9, 26, 35, and 49 GeV measured with the silicon/tungsten

calorimeter of SICAPO Collaboration shown in Fig. 2.78 (reprinted from Nucl. Instr. and Meth. in

Phys. Res. A 235, Barbiellini, G., Cecchet, G., Hemery, J.Y., Lemeilleur, F., Leroy, C., Levman,

G., Rancoita, P.G. and Seidman, A., Energy Resolution and Longitudinal Shower Development

in a Si/W Electromagnetic Calorimeter, 55–60, Copyright (1985), with permission from Elsevier;

see also [Leroy and Rancoita (2000)]). In ordinate with a logarithmic scale, it is shown the energy

deposited, in MeV, in each detector.

deposited per unit of radiation length dE/dt in a lead-glass homogeneous calorime-

ter for primary photons from 0.1 up to 5 GeV [Longo and Sestilli (1975)]. Longo and

Sestilli (1975) determined the parametrization of the shower development given by

Eq. (2.232) and found t

max

values for the simulated showers diﬀering only slightly

from the values calculated via Eq. (2.229). More recently, the mean longitudinal

shower-distribution was studied, in a systematic way, by using simulation codes for

a wide range of elements at energies up to about hundred GeV ([Grindhammer et

al. (1989); PDB (2008)], see also for instance [Iwata (1979, 1980); Fabjan (1985a,

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

204 Principles of Radiation Interaction in Matter and Detection

Fig. 2.78 Electromagnetic calorimeter of SICAPO Collaboration: it was the ﬁrst using silicon

detectors as active samplers (reprinted from Nucl. Instr. and Meth. in Phys. Res. A 235,

Barbiellini, G., Buksh, P., Cecchet, G., Hemery, J.Y., Lemeilleur, F., Rancoita, P.G., Vismara, G.

and Seidman, A., Silicon Detectors and Associated Electronics Oriented to Calorimetry, 216–223,

1986)]). The longitudinal shower distribution is approximately described by

= St

−bt

, (2.232)

where b ≈ 0.5, S = Eb

ω+1

/Γ(ω + 1), E is the incoming particle energy in GeV and

Γ is Euler’s function. More precise values for b as function of A and E/²

can be

found in [Leroy and Rancoita (2000); PDB (2004)] and are shown in Fig. 2.76. The

position of the cascade maximum is located at

max

= ω/b =

+ f

, (2.233)

where f = −0.5 or +0.5 for incident electrons or photons, respectively.

The slow exponential decay of the cascade beyond its maximum is often ex-

pressed as e

−t/λ

att

where λ

att

is the longitudinal attenuation length. For instance,

att

= 1/b according to Eq. (2.232). Measured values of λ

att

(in units of g/cm

and radiation length X

) are listed in Table 2.14 for various absorbers; they show

very little dependence on the incoming particle energy reﬂecting the fact that, at

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 205

Fig. 2.79 The cascade maximum, t

max

(lower curve), and the cascade center-of-gravity, t

(upper

curve), in units of radiation lengths as a function of the incoming-electron energy measured with

the silicon/tungsten calorimeter of SICAPO Collaboration shown in Fig. 2.78 (reprinted from Nucl.

Instr. and Meth. in Phys. Res. A 235, Barbiellini, G., Cecchet, G., Hemery, J.Y., Lemeilleur,

F., Leroy, C., Levman, G., Rancoita, P.G. and Seidman, A., Energy Resolution and Longitudi-

nal Shower Development in a Si/W Electromagnetic Calorimeter, 55–60, Copyright (1985), with

permission from Elsevier; see also [Leroy and Rancoita (2000)]).

large depths, cascading is mainly due to low-energy photons attenuated with rates

corresponding to the respective values of λ

att

The cascade deposits 98% of the incoming-particle energy, i.e., 98% of the shower

is longitudinally contained, at an approximate depth given by [Amaldi (1981)]:

L(98%) ≈ 3 t

] (2.234)

with t

determined by Eq. (2.230). Other approximate expressions can be found

in [Fabjan (1986)]. A further parametrization of the longitudinal shower contain-

ment for 95% longitudinal containment, using available experimental data and cal-

culations [Fabjan (1986)], is given by:

L(95%) = (t

max

+ 0.08Z + 9.6) [X

] (2.235)

with t

max

obtained by Eq. (2.229).

The parametrization of Eq. (2.232) proves to be not fully adequate when applied

to the description of data taken with diﬀerent types of calorimeters, in particular

for low values of E

. Dependences more complex than the one given by Eq. (2.232)

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

206 Principles of Radiation Interaction in Matter and Detection

were already proposed in the analytical formulations of Heisenberg (1946) and

Rossi (1964). Therefore, the parametrization given by Eq. (2.232) has to be im-

proved to account for the modiﬁed experimental conditions. For instance, the lon-

gitudinal behavior of electromagnetic cascades is illustrated in Fig. 2.77 [SICAPO

Collab. (1985a)] for the Si/W calorimeter

∗

shown in Fig. 2.78. The average energy

deposition, i.e., the so-called visible energy (see page 616), was studied as a function

of the depth t for incoming electron energies from 4 up to 49 GeV using that Si/W

calorimeter [SICAPO Collab. (1985a)]. The total depth of the calorimeter was 24 X

with a silicon detector (25 cm

active area) as active sampler every

‡‡

two X

. The

mean dep osited energy, ² (in MeV), in silicon detectors exhibits a steep rise with

the longitudinal depth, followed by a slow decrease. The fall-oﬀ beyond the cascade

maximum displays a two-component structure [SICAPO Collab. (1985a,b)], each

component being approximately exponential with a logarithmic dependence on the

incident energy. The ﬁtted curve, interpolating the experimentally measured values

of ², is expressd by:

² = ²

exp(−b

t) + ²

exp[−u(t − x

) − y

] [MeV], (2.236)

where

= (3.2 ± 0.5) + (0.3 ± 0.2) ln E,

= (0.75 ± 0.10) + (−0.05 ± 0.04) ln E,

= (0.26 ± 0.10) ln E,

u = (0.04 ± 0.02) ln E,

= (−6.8 ± 3.5) + (55.9 ± 20.3) ln E,

= 2.4 ± 0.4,

= (2.2 ± 1.2) + (1.5 ± 0.6) ln E [MeV],

= 1 [MeV] ,

and the incoming particle energy, E, is in units of GeV [SICAPO Collab. (1985a)]. In

this case, the position of the cascade maximum, determined experimentally, in-

creases with the logarithm of the incident energy (in GeV) according to

max

= (3.97 ± 0.24) + (1.02 ± 0.11) ln E. (2.237)

The values of t

max

can be calculated from Eq. (2.229), taking into account that

≈ 8.08 MeV for tungsten absorbers. This leads to

max

= 3.87 + 1.01 ln E

in agreement with Eq. (2.237). The location of the center-of-gravity of the cascade,

, is determined experimentally and given by

= (8.4 ± 0.5) + (0.45 ± 0.17) ln E. (2.238)

∗

This electromagnetic calorimeter was the ﬁrst one employing silicon detectors as active samplers.

‡‡

The usage of silicon detectors for high-energy calorimetry was proposed by [Rancoita and Seid-

man (1984)].

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 207

The location of the cascade maximum, t

max

, and of the cascade center-of-gravity,

, are shown in units of radiation length in Fig. 2.79 as a function of the inco-

ming electron energy for the Si/W calorimeter of [SICAPO Collab. (1985a)]. The

disagreement between the values of t

, as predicted from the “Approximation

B” [Eq. (2.230)], and the values determined experimentally, i.e., those given in

Eq. (2.238), is partially due to the extent of low-energy photon penetration (both

lateral and longitudinal) in the absorber. The Compton and photoelectric eﬀects

were completely neglected in Rossi’s formulation of shower propagation.

2.4.2.3 Lateral Development of Electromagnetic Showers

During the cascade development, the energy is degraded into low-energy electrons

via ionization, Compton scattering and photoelectric interactions, which generate

electrons dissipating their energies mainly (or to a large extent) by collision. The

cascade lateral-spread

∗∗

is caused by several physical processes. The photoelectric

and Compton scattering generate secondary electrons which are no longer aligned

with incoming-photon directions and can be even emitted in the backward hemi-

sphere in the case of photoelectric electrons. Also, secondary Compton photons

∗

are no longer along primary-photon directions, thus contributing to the widening

of the cascade. Furthermore, multiple Coulomb scatterings, of those electrons that

cannot radiate but have enough energy to travel away, lead to the spread of electron

directions out of the axis deﬁned by the primary particle direction.

The transverse depth unit of a cascade is the Moli`ere radius and is deﬁned as

, (2.239)

where E

= 21.2 MeV (see page 122), and ²

is the critical energy [Eq. (2.121)]. Va-

lues of R

for various absorbers are listed in Table 2.3. For rapid estimates of the

Moli`ere radius, the following expression can be used [Amaldi (1981)]:

≈ 7

, (2.240)

where R

is the Moli`ere radius in g/cm

, with

∆R

g M

≤ 10% for Z ≥ 13.

In a material made of several absorbers, when none of them is negligible in units of

, an estimate of the overall Moli`ere radius can be obtained from the expression

g M

c,i

g 0 i

, (2.241)

where f

, ²

c,i

and X

g 0 i

(in g/cm

) are the weight fraction, critical energy and

radiation length of the ith absorber, respectively. The transverse development of

∗∗

It is the shower development along the direction orthogonal to that of the primary particle.

∗

These photons may be backward scattered.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

208 Principles of Radiation Interaction in Matter and Detection

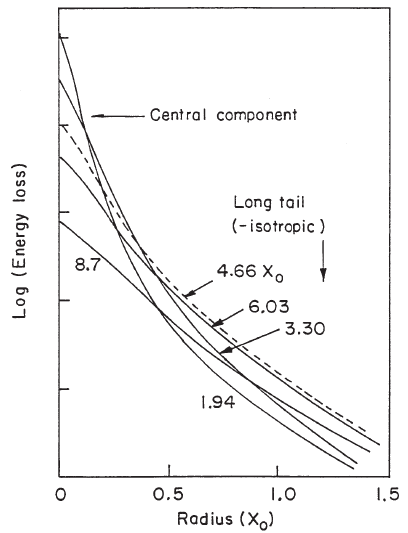
Fig. 2.80 Radial shower proﬁle of 1 GeV electrons in aluminum, i.e., the lateral distribution

of energy loss (in arbitrary units) in the shower versus the radial position in radiation lengths

(from [Leroy and Rancoita (2000)]; computed curves from [Yuda et al. (1970)]).

electromagnetic cascades in diﬀerent materials (from low- and medium-Z like Cu

to high-Z like Pb) scales fairly accurately with R

[Nelson et al. (1966); Crannell

(1967); Bathow et al. (1970)]. Energy is deposited beyond the cylindrical volume

deﬁned in units of the Moli`ere radius. For instance, as much as 10% of the energy is

deposited beyond the cylinder with a radius of ≈ 1R

. The 95% radial containment

) for electromagnetic cascades is given by

(95%) = 2R

. (2.242)

The experimental data available in [Yuda (1969); Yuda et al. (1970); Nakamoto

et al. (1986); Bormann et al. (1987); De Angelis (1988); SICAPO Collab. (1988a,

1989a, 1991a)] show that the cascade radial proﬁle presents complex features

(Figs. 2.80−2.82) requiring an elaborate description [SICAPO Collab. (1988a,

1991a)]. Furthermore, the experimental data indicate (Figs. 2.81−2.84) that the

lateral distribution of the shower is mainly determined by the thicker (in units of

) shower absorber if there is an additional small (in units of X

) absorber, as in

most cases for readout materials in sampling calorimeters. In Figs. 2.81−2.82, the

lateral and longitudinal distributions of the shower for 6 GeV electrons are shown

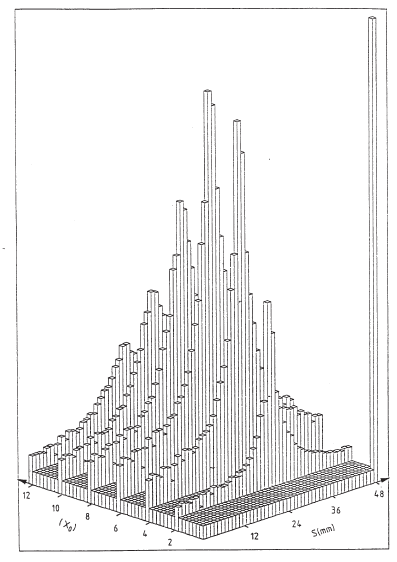
January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 209

every 2 X

(≈ 7 mm) of tungsten [SICAPO Collab. (1989a)]. In Figs. 2.83−2.84,

the experimental data (at the same energy and with the same readout detectors)

were taken inserting 5 mm of G10 absorber (≈ 2.6%X

) in the middle of the 2 X

tungsten absorbers [SICAPO Collab. (1989a)]. Although the step length is 7 mm

(2 X

of tungsten) for the former set of two experimental data and 12 mm for the

latter two, the distributions are similar.

The lateral distribution of the shower depends on the calorimeter depth at which

it is measured. At least, a two-component structure is needed to describ e the trans-

verse proﬁle of the electromagnetic cascade which displays a narrow central and a

broad peripheral part [De Angelis (1988); SICAPO Collab. (1988a, 1991a)]. The

central part scales as R

, and is mainly due to multiple-scattering eﬀects pro-

duced by the fast electrons responsible for the deposition of most of the incident

Fig. 2.81 Lateral distribution of the shower for 6 GeV electrons in tungsten absorber up to 12 X

in steps of 2 X

, S being the 1 mm pitch strip number of the readout silicon detector (adapted

from Nucl. Instr. and Meth. in Phys. Res. A 279, Lemeilleur, F., Lamarche, F., Leroy, C.,

Paludetto, R., Pensotti, S., Rancoita, P.G., Vismara, L. and Seidman, A., Longitudinal and trans-

verse development of electromagnetic showers using silicon detectors, 66–72, Copyright (1989),

with permission from Elsevier; see also [Leroy and Rancoita (2000)]). The vertical axis is in arbi-

trary units.