Leroy C., Rancoita P.-G. Principles Of Radiation Interaction In Matter And Detection

Подождите немного. Документ загружается.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

230 Principles of Radiation Interaction in Matter and Detection

Fig. 3.4 Possible decays of nuclide with the mass number M

= 101. The arrows indicate β-

decays (adapted and reprinted with permission from [Segre (1977)]). The origin on the ordinate

(mass scale) is chosen arbitrarily. The atomic number Z is shown in abscissa.

3.1.4.1 The β-Decay and the Nuclear Capture

Let us consider the semi-empirical mass formula derived by von Weizs¨acker and

Bethe, given in Sect. 3.1.1.1, for isobars with atomic mass M

(Z, M

). Equa-

tion (3.14) can be rewritten as:

(Z, M

) = c

− c

Z + c

√

where

= a

+ a

−1/3

= (m

− m

− m) + a

1/3

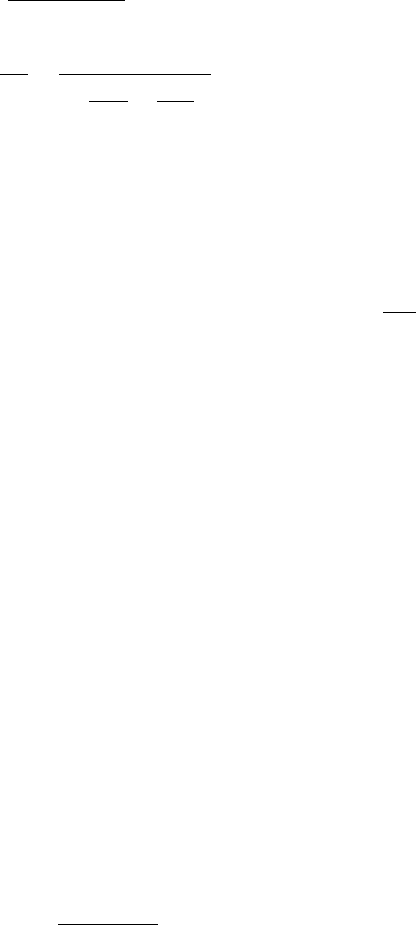
January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Nuclear Interactions in Matter 231

The parameters δ

, a

and a

are given at page 223. From this equation, we

see that the isobar mass depends on Z and Z

. The isobar mass minimum is found

by imposing that

∂M

(Z, M

)

∂Z

= 0,

i.e., for

Z =

≈

93.93

0.714

1/3

93.15

. (3.24)

For any odd M

value, the resulting nuclear mass depends on Z following a

parabolic curve. For instance, the isobar with M

= 101, in Fig. 3.4, has a mi-

nimum corresponding to Z = 44 (

101

Ru), as computed by means of Eq. (3.24). In

Fig. 3.4, we see that isobars with neutrons in excess decay with the process given

in Eq. (3.21) and emit β

−

particles. Isobars, with protons in excess, decay with

the process expressed by Eq. (3.22) and emit β

particles. However, for nuclides

with even M

value, the decay curves are diﬀerent for even-even nuclei and odd-

odd nuclei. The curves are separated by a term depending twice on δ

√

. In

particular, for heavy nuclei with M

> 70, more than one β-stable nuclide exist,

as shown in Fig. 3.5 for isobars with M

= 106. The nuclei

106

Pd [as predicted by

means of Eq. (3.24)] and

106

Cd are on the lower parabolic curve. The nuclide

106

is β-stable, because the neighboring odd-odd nuclides have larger masses.

As mentioned at page 228, a nucleus can decay via electron capture. The electron

has a ﬁnite probability to be inside the nuclide and to allow the proton transforma-

tion into a neutron and a neutrino [Eq. (3.23)]. This reaction occurs especially for

the case of heavy nuclei, in which K-electrons are close to the nucleus. As a result

of a K-capture, an outer electron can occupy the inner vacant energy level. Con-

sequently, a characteristic X-ray can be emitted. In Appendix A.6, half-lives and

end-point energy emissions are shown for some commonly used radioactive β

and

−

sources, from [PDB (2000)].

3.1.4.2 The α-Decay

The spontaneous emission of an α -particle by some (heavy) nuclei (see Ap-

pendix A.6) is related to the compactness of the He nucleus whose binding energy

is ≈ 7 MeV/nucleon (see Fig. 3.1). Thus, more energy is available for the decay

process. However, the α-particle has to penetrate a region of very large potential

energy near the nuclear surface. In fact, the α-particle is subjected to a combination

of short-range attractive nuclear forces, represented by a square-well potential, and

long-range electromagnetic repulsive forces, represented by a Coulomb potential

2 (Z − 2) e

For a purely electrostatic Coulomb potential barrier, like the one encountered

centrally by a positively charged particle, the potential-energy height is determined

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

232 Principles of Radiation Interaction in Matter and Detection

Fig. 3.5 Possible decays of nuclide with the mass number M

= 106. The arrows indicate β-

decays (adapted and reprinted with permission from [Segre (1977)]). The origin on the ordinate

(mass scale) is chosen arbitrarily. The atomic number Z is shown in abscissa.

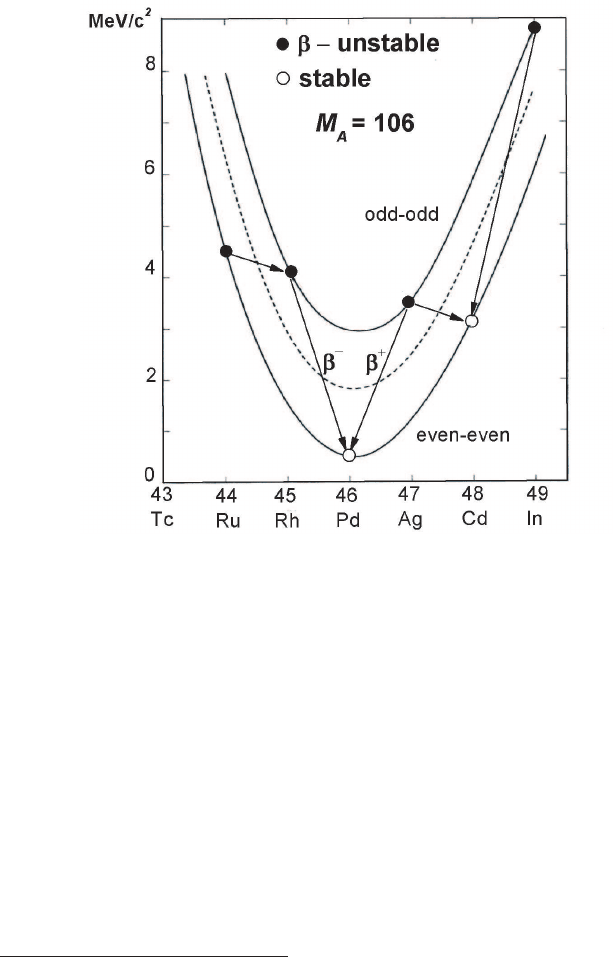
by the nuclear radius r

(Fig. 3.6). For instance, in the case of an α-particle escaping

centrally

∗

from an

238

U nucleus, the Coulomb barrier is ≈ 24 MeV. In classical

mechanics, the potential barrier would prevent such an emission.

The penetration of the p otential energy barrier is a quantum-mechanical ef-

fect. Its probability depends on the shape and height of the potential-energy barrier,

as well as on the kinetic energy of the emitted α-particle. In turn, the probability

is related to the lifetime of the decaying nucleus. According to quantum theory,

there is a ﬁnite probability of tunneling through the barrier, the so-called tunneling

eﬀect, even for α-particle kinetic energies lower than the barrier height. It can be

qualitatively understood with the aid of Heisenberg’s uncertainty relation

‡‡

. For

an α-particle of momentum p, we have (e.g., see Equation 4.15 in Chapter IV

∗

An extended discussion on the Coulomb barrier, including non-central cases, is presented in

Chapter 7 of [Marmier and Sheldon (1969)] and Chapter 7 of [Segre (1977)].

‡‡

In Chapter IV (Section 3), Finkelnburg (1964) noted that there are diﬀerent methods of deducing

the uncertainty principle. These methods lead to diﬀerent terms at the right-hand side of Eq. (3.25),

namely h, ~ or ~/2, depending on the deﬁnition of the uncertainty 4. In Eq. (3.25), the maximal

uncertainty is taken into account with the term h, whereas the smaller values correspond to the

mean or the most probable uncertainty, respectively.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Nuclear Interactions in Matter 233

alpha-particle

Fig. 3.6 Coulomb potential energy of an α-particle as a function of the distance r from the

center of a nucleus of radius r

(adapted and reprinted with permission from Povh, B., Rith, K.,

Scholz, C. and Zetsche, F. (1995), Particles and Nuclei: an Introduction to the Physical Concepts,

Figure 3.5, page 31, Springer-Verlag Publ., Berlin Heidelberg New-York;

° by Springer-Verlag

1995).

of [Finkelnburg (1964)]):

4p 4 x ≈ h. (3.25)

For a non-relativistic velocity v, because 4p cannot be larger than the particle

momentum, we get:

4x ≥

where h/(m

v) is the de Broglie wavelength and m

is the α-particle rest

mass. Thus, if the velocity is such that 4x exceeds the barrier width at that energy,

there is a ﬁnite probability that the α-particle ﬁnds itself on the other side of the

barrier.

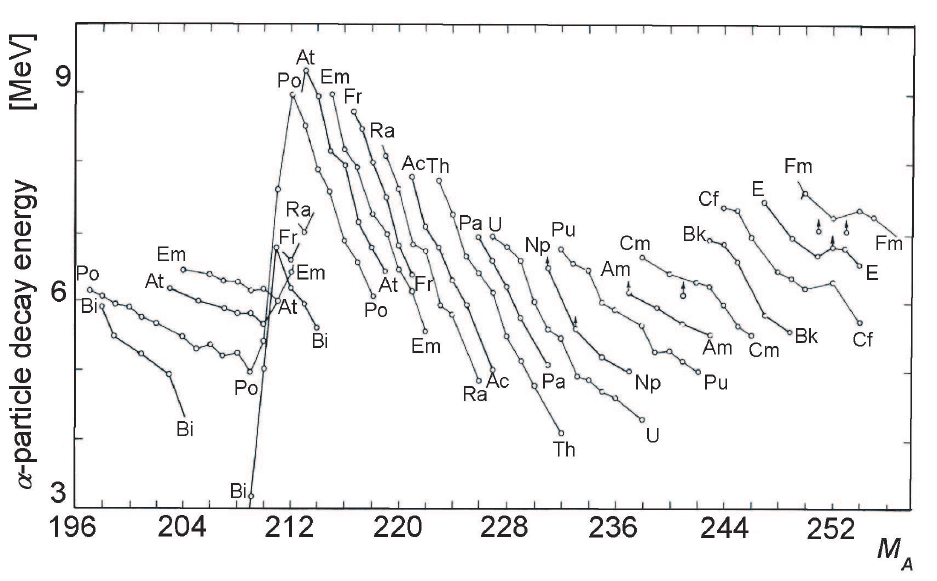
The fact, that only a few nuclei with

150 ≤ M

≤ 210

are active α-emitters, can be related to the relative small available decay ener-

gies. For M

≥ 210 (Fig. 3.7, see [Rasmussen (1965); Segre (1977)]), decay energies

are larger. Hence, heavy nuclei are favored as α-emitters. The resulting half-lives

can be long and are given in Appendix A.6. An example of an α-particle emit-

ter is the

238

U nuclide which, together with its decay products, contributes to the

natural radioactivity background; the

222

Rn gas can be assimilated by man and is

responsible for about 40% of the natural radioactivity average exposure of human

beings.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

234 Principles of Radiation Interaction in Matter and Detection

Fig. 3.7 α-particle decay-energy in MeV as a function of the atomic mass number M

for heavy nuclei (adapted and reprinted with permission

from [Rasmussen (1965)]). The lines connect isotopes.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Nuclear Interactions in Matter 235

3.1.5 Fermi Gas Model and Nuclear Shell Model

The presence of an internal nuclear structure was observed by electron scattering

experiments on nuclei, which show a remarkable diﬀerence with results obtained by

electron–proton elastic scattering.

In elastic electron scattering on proton, the emerging electron energy is related

to the electron scattering angle. Let us consider the invariant mass of the electron–

proton system and indicate with

˜p = (E/c, ~p) ,

P = (m

c, 0) , ˜p

= (E

/c, ~p

) ,

/c,

the four-momentum of the incoming electron, the target proton at rest, the scattered

electron and the recoil proton, respectively, with total energies E, m

, E

and

momenta ~p, 0, ~p

, respectively, where m

is the proton rest-mass. By considering

the invariant mass of the reaction (see page 11), we get:

(˜p +

P )

= (˜p

)

⇒ ˜p ·

P = ˜p

. (3.26)

Furthermore, from four-momentum conservation, we derive:

˜p +

P = ˜p

⇒

= ˜p +

P − ˜p

; (3.27)

thus, by inserting

from Eq. (3.27) in Eq. (3.26), we obtain:

E m

= ˜p

· ˜p + ˜p

P − p

− ~p · ~p

+ E

− p

. (3.28)

In addition, we have that

˜p

· ˜p

= p

= m

(m is the electron rest mass) and, in the case of energetic electrons,

E ≈ p c, E

≈ p

Since the electron mass can b e neglected, Eq. (3.28) becomes:

E m

− pp

cos θ + E

− m

−

cos θ + E

where θ is the scattering angle of the electron. Finally, we get:

1 + [E/ (m

)] (1 − cos θ)

, (3.29)

which shows that the electron recoil-energy is directly correlated to the scattering

angle.

However, in the case of electron scattering on nuclei, which contain many nu-

cleons, the energy spectrum is more complex. For instance, in the experiment of elec-

tron scattering on H

O at incoming energy of 246 MeV (see Chapter 6 of [Povh, Rith,

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

236 Principles of Radiation Interaction in Matter and Detection

Scholz and Zetsche (1995)]), the scattered electron energy spectrum at θ = 148.5

◦

shows a narrow peak at ≈ 160 MeV (which corresponds to the elastic electron scat-

tering on the proton of the hydrogen) and a smooth continuous background. The

continuous energy sp ectrum, which has a broad peak slightly lower than the elastic

peak, is due to the elastic electron scattering on

O nucleons. This process is called

quasi-elastic scattering. The broadening and shift of the quasi-elastic peak can be

understoo d in terms of an elastic interaction on a bound nucleon, which requires a

certain amount of energy being emitted from the nucleus, and the presence of an

internal nucleon motion inside the nucleus. Quasi-free nucleons, inside the nucleus,

modify the process kinematics and account for the peak broadening.

The simplest nuclear model, that accounts for momentum distribution of nu-

cleons, is the free nucleon Fermi gas model, which was proposed by Fermi 1950

(e.g., see Section H in Chapter VIII therein). In this model, the overall eﬀect

of nucleon–nucleon interactions results in a square potential well, as shown in

Fig. 3.8. Nucleons with spin

do not have a ﬁxed p osition inside the nucleus,

but are free to move and constitute a degenerate Fermi gas (see page 810). The

nucleons will obey the Fermi–Dirac statistics (Appendix A.7), which in turn ac-

counts for the Pauli exclusion principle. The nuclear potential is zero outside the

potential-well. At 0 K, since each state cannot contain more than two nucleons of

the same kind, we can rewrite Eq. (A.3) of Appendix A.7 for neutrons and protons

as:

)

= ~

3π

nucl

2/3

⇒ p

= ~

3π

nucl

1/3

, (3.30)

)

= ~

3π

nucl

2/3

⇒ p

= ~

3π

nucl

1/3

, (3.31)

where V

nucl

is the nuclear volume, p

and p

are the Fermi momenta of neutrons

and protons, respectively. To a ﬁrst approximation, for a nucleus with

= Z =

and nuclear radius given by Eq. (3.12) (and consequently with V

nucl

πr

the Fermi momentum, p

, of the nucleons becomes:

= p

= ~

3π

nucl

1/3

= ~

3π

πr

1/3

9π

1/3

≈ 250 MeV/c.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Nuclear Interactions in Matter 237

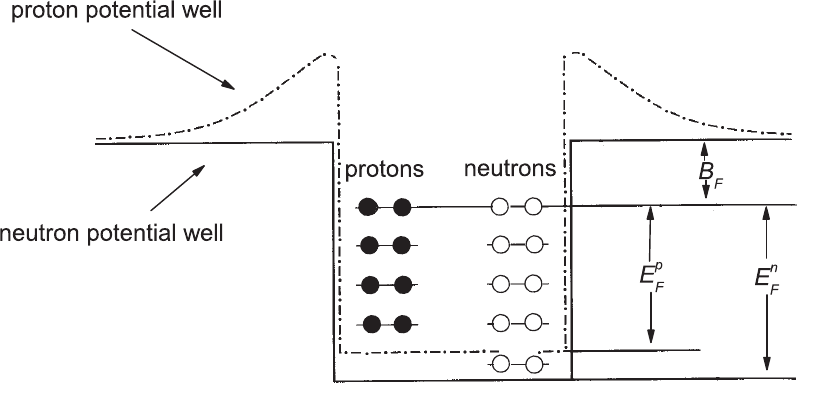
Fig. 3.8 Potential wells and states for neutrons and protons in the framework of the Fermi gas model of the nucleus (adapted and reprinted with

permission from Povh, B., Rith, K., Scholz, C. and Zetsche, F. (1995), Particles and Nuclei: an Introduction to the Physical Concepts, Figure 17.1,

page 225, Springer-Verlag Publ., Berlin Heidelberg New-York;

° by Springer-Verlag 1995).

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

238 Principles of Radiation Interaction in Matter and Detection

Table 3.2 Nuclear shells, value of l and j (which appears as subscript), number

of particles in the shell and total maximum number of particles including the ones

in the shell (see Section 2 in Chapter XIV of [Blatt and Weisskopf (1952)] and

references therein).

Nuclear Terms No. of particles No. of particles

shells in up to and

) shell including shell

I s

1/2

2 2

II p

3/2

, p

1/2

6 8

IIa d

5/2

6 14

III s

1/2

, d

3/2

6 20

IIIa f

7/2

8 28

IV p

3/2

, f

5/2

, p

1/2

, g

9/2

22 50

V g

7/2

, d

5/2

, d

3/2

, s

1/2

, h

11/2

32 82

VI h

9/2

, f

7/2

, f

5/2

, p

3/2

, p

1/2

, i

13/2

44 126

This result is in general agreement with measurements obtained from quasi-elastic

electron nuclear scattering [Moniz et al. (1971)]; except in light nuclei, the Fermi

momentum is found to be (240–260) MeV and almost independent of M

. For light

nuclei, the Fermi momentum is lower than expected: for these nuclei, the Fermi gas

nuclear model is not suﬃciently adequate.

In a stable nucleus, the potential-energy diﬀerence between the bottom level of

the square potential well and the level corresponding to nucleons with the largest

kinetic energy (i.e., the Fermi energy) is given by the value of the Fermi level. For

≈ 250 MeV/c, the Fermi energy is

nucl

≈ 33 MeV

(where m

nucl

is the mass of the nucleon, see Sect. 3.1). Furthermore, the energy

diﬀerence, indicated by B

in Fig. 3.8, between the top level of the square potential

well and the Fermi level is about (7–8) MeV. B

is the average binding energy per

nucleon as mentioned at page 219. Hence, the total potential depth is ≈ 40 MeV. The

average kinetic energy of the nucleon [see Eq. (A.5) in Appendix A.7] is

, of

the same order as the p otential depth.

In stable nuclei, the Fermi levels of protons and neutrons are the same

∗

. However,

because these nuclei have an excess of neutrons and because neutrons and protons

occupy the same nuclear volume, the expected Fermi energies (E

and E

) from

Eqs. (3.30, 3.31) are diﬀerent. Thus, the potential depth for neutrons must be

deeper (Fig. 3.8), as proposed by Fermi (e.g., see the already mentioned Section H

in Chapter VIII of [Fermi (1950)]). As a result, protons are in general less bound

than neutrons.

∗

If the Fermi levels of protons and neutrons were diﬀerent, the nucleus could vary the energetic

conﬁguration via β-decay, i.e., the nucleus would be unstable.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Nuclear Interactions in Matter 239

Another particular nucleus feature is the existence of the so-called magic number

nuclei. It has been observed that nuclei, for which Z or M

−Z or both are equal to

2, 8, 14, 20, 28, 50, 82, 126, have distinctive characteristics, i.e., the largest binding

energies (like the nuclides with N

= 20, 28, 50 and 82) and much higher cosmic

abundances (as, for instance, the nuclei

He,

Si,

Ca). Furthermore, the

stable isotope

208

Pb is characterized by the magic neutron number 126 and proton

numb er 82. In atomic physics, an analog case is the stability of inert elements, which

is attributed to the ﬁlling of electron shells. Similarly, the magic number nuclei are

considered as an indication of the presence of a nuclear shell structure.

In the nuclear shell model

, the interaction of any nucleon with remaining nu-

cleons inside the nucleus is represented by a static potential well. The potential well

is similar in both extension and shape to the nuclear density distribution. Energy

levels in the potential well consist of a series of single particle energy-levels E(n, l),

where (as in atomic physics) n is the principal quantum number and l is the orbital

angular momentum quantum number. Their relative spacing is a function of the

shape and depth of the potential well. Protons and neutrons ﬁll these levels, but

the number of particles in each level is determined by the Pauli exclusion princi-

ple. However, in 1948, Mayer and Jensen demonstrated that, because of the spin

dependence of nuclear forces, there is a strong spin-orbit potential coupling which

results in splitting the (n, l) energy-level in two sublevels (n, l, j) with j = l ±

i.e., there is a spin-orbit coupling which splits the sublevels with j = l −

and

j = l +

, so that the latter one

is at lower energy. The overall eﬀect is the shell

assignment shown in Table 3.2. The shell model also predicts the value of magnetic

moments for odd-even and even-odd nuclei. The assignment of deﬁnite l values to

proton- or neutron-odd nuclei can also be used in the theory of β-decay, in which

the decay probability depends on the spin diﬀerence between the decaying nucleus

and the decay product. A remarkable success of the shell model was its capability

to predict that certain β-transitions should exhibit forbidden-type spectra. In ad-

dition, the model was able to explain why almost all isomeric states (see page 226)

have long lifetimes.

3.1.5.1 γ Emission by Nuclei

A nucleus can have excited states from which it decays via γ-emission. These nu-

clear de-excitations provide information on quantum numbers and energy levels of

nuclei. Above the ground state, there are many levels with characteristics J

(spin

J and parity P ) quantum numbers.

In general, the excitation of an even-even nucleus has the consequence of break-

The reader can see Chapter 17 of [Henley and Garcia (2007)] for a recent review and references

on the nuclear shell model.

In this level, the intrinsic spin is parallel to the orbital angular momentum. In addition, this

eﬀect is assumed to increase with increasing values of l (e.g., see Section 2 of Chapter IV of [Blatt

and Weisskopf (1952)]).