Leroy C., Rancoita P.-G. Principles Of Radiation Interaction In Matter And Detection

Подождите немного. Документ загружается.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

250 Principles of Radiation Interaction in Matter and Detection

Fig. 3.12 Ratio of the total cross section on nucleon of a coherently produced system over the cross

section on a free proton as a function of the produced invariant-mass from [Rancoita and Seidman

(1982)] (Copyright of the Societ`a Italiana di Fisica): a) σ

pππ

/σ

for the reaction p + A → pππ +A

(data ◦ at 15.3 GeV from [M¨uhlemann et al. (1973)] and x at 22.5 GeV from [Rosen (1977)]); b)

3π

/σ

for the reaction π + A → πππ + A (data ◦ at 15.0 GeV from [M¨uhlemann et al. (1973)],

data x at 22.5 GeV from [Rosen (1977)] and data • at 40.0 GeV from [Bellini et al. (1981)]).

the additivity of the phase shifts from scattering by various nucleons, ii) the small

scattering angles, which is equivalent to neglecting the longitudinal component of

the momentum transfer q

, and iii) the so-called frozen nucleus approximation whose

consequence is to consider stationary target nucleons, so that nuclear wave func-

tions are represented, in the scattering amplitude, by a simple average of scattering

amplitudes from ﬁxed centers [Glauber (1959)]. The scattering amplitude is related

to a multiple scattering series amplitude, which accounts for single and multiple

nucleon interactions. An extension of the theory to large A-nuclei is known as the

optical model.

The high-energy coherent-dissociation on nuclei was treated, in the framework of

the Glauber theory [K¨olbig and Margolis (1968)], assuming that a multiple sequence

of interactions, initiated in a nucleus, occurs through single interactions with one or

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Nuclear Interactions in Matter 251

more target particles. The incoming particle and the outgoing particle are considered

to undergo elastic scatterings, before and after the production took place on a

nucleon. In the case of the reaction given in Eq. (3.38), by i) extending the Glauber

formalism, ii) ignoring the Coulomb distortion, iii) assuming that the interaction

does not depend on the target quantum numbers, and iv) using the optical theorem

[Eq. (3.44)], the coherent diﬀerential cross section as a function the four-momentum

transfer becomes [K¨olbig and Margolis (1968)]:

dσ

coh

dσ

h−nucl

t=0

G(q)

(σ

− σ

∗

)

+ (α

− α

∗

)

, (3.49)

where (dσ

h−nucl

/dt)

t=0

is the diﬀerential cross section for the reaction (3.38) on

nucleon at t = 0; α

and α

∗

are the ratio of the real to the imaginary parts of

the scattering amplitudes on nucleons; σ

and σ

∗

are the total cross sections on

nucleon and, ﬁnally, G(q) is given by

~q ·

exp

−

(1 − iα

) σ

− exp

−

(1 − iα

∗

) σ

∗

¸¾

in which

b plays the role of the impact parameter; J

is the cylindrical Bessel

function of the ﬁrst kind of order zero; and T

, called the surface thickness of

the target, is deﬁned in cylindrical coordinates

(

b, z) as

= A

+∞

−∞

ρ(

b, z) dz,

where ρ(~r) describes the single-particle density function

of the nucleus, with

ρ(~r) d~r = 1.

At high energy, the scattering amplitudes on nucleons are mainly imaginary and

Eq. (3.49) can be rewritten to a good accuracy as:

dσ

coh

dσ

h−nucl

t=0

;

∗

; q

, (3.50)

where

;

∗

; q

(σ

− σ

∗

)

~q ·

exp

−

− exp

−

∗

¸¾

b. (3.51)

The coherent production theory was used to determine the values of the total

cross section of unstable particles, like meson resonances, whose cross sections are

In these coordinates, z is the beam direction, i.e., the longitudinal coordinate.

It is assumed to be equal for neutrons and protons.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

252 Principles of Radiation Interaction in Matter and Detection

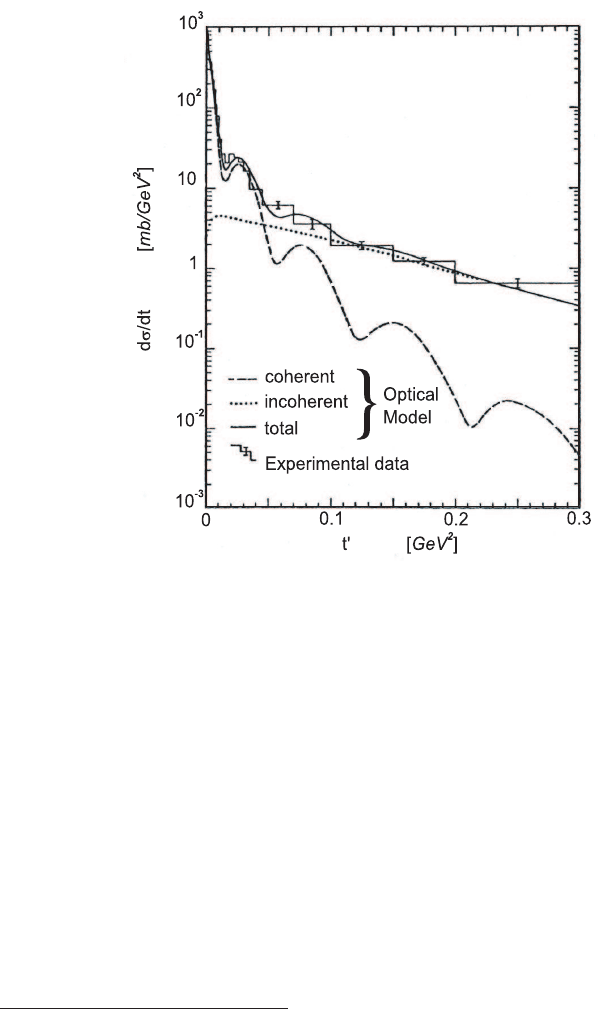
Fig. 3.13 Coherent and incoherent contributions to the diﬀerential cross section for 3π production

on silver in the A

meson-resonance mass-region as a function of t

[deﬁned in Eq. (3.42)] in

relativistic units (adapted with permission from [Rosen (1977)]).

represented by the term σ

∗

in Eqs. (3.49, 3.50). The A-dependent cross section

∗

can be extracted from measured coherent cross sections on nuclei in both hadro-

and photo-production experiments (e.g., see [M¨uhlemann et al. (1973); Beusch et

al. (1975); Rosen (1977); Bellini et al. (1981)]). For instance [Rancoita and Sei-

dman (1982)], in Fig. 3.12 the total cross sections of the pππ and 3π systems,

produced coherently on nuclei, are shown as functions of the ﬁnal-system invariant-

mass (experimental data are from [M¨uhlemann et al. (1973); Rosen (1977); Bellini

et al. (1981)]). In ordinate, the values are normalized to the p–p and π–p cross sec-

tions, respectively. The cross sections of ﬁnal system-states are found to be smaller

than the incoming particle cross sections on nucleon and decrease with increasing

the produced system invariant-mass. The apparent increase of the ﬁnal-state cross

section was related to the possibility that the production process is more complex

∗

It was experimentally demonstrated that the coherent production cross section depends on the

(spin J and parity P ) state of the ﬁnal system (e.g., see [Beusch et al. (1975); Perneger et al.

(1978)]).

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Nuclear Interactions in Matter 253

than a simple one-step reaction (e.g., see [F¨aldt (1977)]) or that the produced state

is not in its asymptotic condition (see, also, data shown in Sect. 3.2.3). Moreover, in

order to produce a well deﬁned ﬁnal-state and a target to recoil in its ground state,

the exchanged particle with the interacting one cannot carry arbitrary quantum

numb ers, i.e., it must respect selection rules. A detailed summary of selection me-

chanisms and selection rules in hadro- and photo-production on nuclei are beyond

the scope of this b ook, and can be found, for instance, in [Bingham (1970)].

Calculations were extended to the case in which the coherent condition of

Eq. (3.45) is no longer satisﬁed, i.e., to the case of incoherent reactions. In the

limit

→ σ

∗

= σ and

¿ 1,

the diﬀerential cross section becomes (see [K¨olbig and Margolis (1968); Bingham

(1970)] and references therein):

dσ

incoh

dσ

h−nucl

N (A; σ

; σ

∗

; q) . (3.52)

In Fig. 3.13, the diﬀerential cross section is shown in relativistic units

∗

for the

production of the A

meson resonance on Ag nuclei by π

−

at 23 GeV [Rosen (1977)],

with the predicted coherent and incoherent cross sections. The coherent production

dominates at low t

values, while, at large values, the incoherent production becomes

more and more important. A review, together with a theoretical introduction to this

ﬁeld, can be found in [Gottfried (1972)].

It has to be noted that there is another type of coherent interaction on nu-

clei, i.e., the electromagnetic interaction of the incoming particle with the nuclear

Coulomb-ﬁeld. In this case, the interaction occurs with a virtual photon of the nu-

clear Coulomb-ﬁeld, and the process is known as the Primakoﬀ eﬀect [Primakoﬀ

(1951)]. The angular diﬀerential cross section for such a reaction was derived [Hal-

prin et al. (1966)] for nuclei of spin zero and charge Ze, characterized by a form

factor F (q

) (see deﬁnition at page 224), where q is the three-momentum trans-

fer. In a Coulomb coherent production for the process expressed by Eq. (3.38), the

particle h

∗

shall have the decay channel h + γ with a radiative decay width Γ

γ,h

. At

high energy

‡

for large nuclear masses, an incoming particle h with spin S

and a

produced particle h

∗

with spin S

∗

(which in turn decays into a multi-particle sys-

tem X), the Coulomb angular diﬀerential cross section is given by [Halprin et al.

(1966)]:

dσ

dΩ

= 8Z

α|F (q

γ,h

∗

1 −

∗

h,h

∗

(θ

+ δ

)

∗

→X

∗

, (3.53)

∗

In these units, we have ~ = c = 1; see, also, page 5.

‡

At high-energy, the momentum p of the outgoing system is approximately equal to its energy E

and approximately equal to the incoming particle energy.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

254 Principles of Radiation Interaction in Matter and Detection

where θ is the scattering angle,

δ =

∗

− m

2 E

' E

(θ

+ δ

);

∗

and Γ

∗

→X

are the decay widths of h

∗

and h

∗

→ X, respectively; Ξ

h,h

∗

h,h

∗

+ 1

(3.54)

with

= 1, for h 6= γ,

, for h = γ,

= 1, for m

6= 0,

(2S

+ 1), for m

= 0.

For instance, reactions of the type K

+γ

→

∗0

(892) → K

−

+π

were investiga-

ted by means of the Coulomb coherent production (e.g., see [Carithers (1975)]). The

particles K

and

∗0

(892) have spin 0 and 1, respectively; then, from Eq. (3.54)

∗0

(892)

= 3. Furthermore, we have that

∗0

(892)→K

−

+π

∗0

(892)

' 1.

Because the production is peaked in the forward direction (namely at small scatte-

ring angles), we obtain from Eqs. (3.40, 3.42, 3.48):

⊥

δ '

+ δ

+ q

⊥

−t

;

in addition,

dΩ = sin θ dθ dφ ' d

dφ '

dφ.

Thus, Eq. (3.53), once integrated on the azimuthal angle φ, becomes:

dσ

= 24παZ

|F (q

∗0

(892)

∗0

(892)

∗0

(892)

− m

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Nuclear Interactions in Matter 255

3.2.3 Multiplicity of Charged Particles and Angular-Distribution

of Secondaries

At high and very high energy, the incoherent production on nuclei was ﬁrst in-

vestigated by cosmic rays physicists using photographic emulsions [Blau (1961)],

mainly. In the study of hadron–nucleus collisions, the nuclear emulsion was used as

both target and detector; it consists of hydrogen, a light group of CNO-elements

and a heavy group of Ag-Br-elements. The mean atomic weight of the emulsion

nuclei is ≈ 60; while for light and heavy nuclei the mean atomic weights are ≈ 14

and 94, respectively.

As already mentioned, one of the salient features in high-energy hadro- and

photo-production is the absence of a strong cascading eﬀect inside the nucleus

(e.g., see [Feinberg (1972); Busza (1977); Otterlund (1977); Halliwell (1978); Ot-

terlund (1980)] and references therein). For instance, existing data from emulsion

experiments, both in cosmic rays [Otterlund (1977); Rancoita and Seidman (1982)]

and accelerators [Busza (1977); Halliwell (1978)], cover a large energy-range and

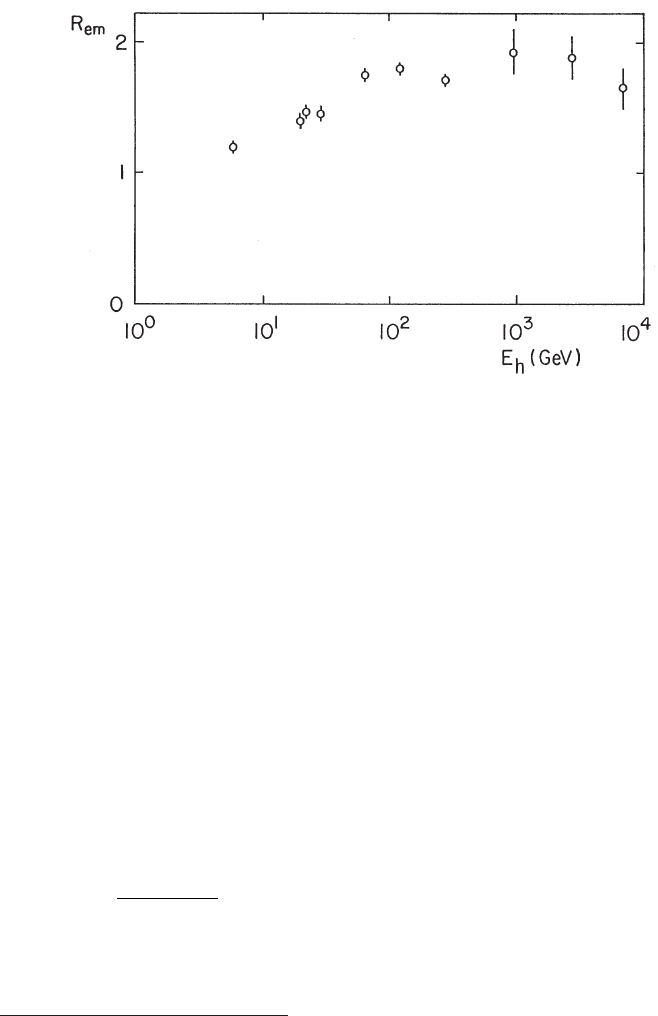
show that the ratio

is less than 2 and, additionally, has a weak (if any) energy dependence on incoming

hadron-energy for E

> 60 GeV (Fig. 3.14): hn

is the average multiplicity of

shower particles

∗∗

produced in interactions with emulsion nuclei and hn

is the

average multiplicity of shower particles produced in hadron–nucleon interactions.

The relationship between the average number of shower particles produced in

hadron–nucleon interaction hn

and the corresponding produced on proton hn

is given by:

= hn

i − 0.5. (3.55)

In a hadron–nucleus interaction, the multiplicity of the produced shower charged

particles is compared to hn

in order to take into account, in a better way, the

admixture of target nucleons and the number of fast recoiling protons identiﬁed

as shower particles (a number which is not very well known). In a hadron–proton

collision (e.g., [Busza (1977)]), the observed average multiplicity of charged particles

is:

i ∼ 1.768 ln s − 2.8,

where s (deﬁned at page 12) is the square of the total center-of-mass energy divided

by c

and in GeV/c

The phenomenon of the weak cascading eﬀect inside the nucleus was systemati-

cally studied in accelerator experiments, using other nuclei as targets. The average

multiplication of particles inside a nucleus is given by

∗∗

The shower particles are charged relativistic-particles with β > 0.7.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

256 Principles of Radiation Interaction in Matter and Detection

Fig. 3.14 The ratio R

= hn

/hn

versus the hadron incoming energy E

(from [Rancoita

and Seidman (1982)], Copyright of the Societ`a Italiana di Fisica; and [Busza (1977)]).

where hn

is the average number of shower particles produced by hadrons inter-

acting on a nucleus of atomic weight A. The observed value of R

is lower than 2.7,

even for massive nuclei.

No naive intranuclear cascade model can account for such a low value of R

and

the energy dependence of R

for incoming hadron-energies up to 10

GeV, under

the assumption that the cross sections of produced relativistic-particles are of the or-

der of the hadron–proton cross section, i.e., 30–40 mb [Denisov et al. (1973); Busza

(1977); Halliwell (1978); Otterlund (1980); Rancoita and Seidman (1982)]. Nev-

ertheless, both the total and the inelastic hadron–nucleus cross sections, and, in

addition, the average number of inelastic interactions

∗

, ¯ν, inside the nucleus can be

derived in the framework of the Glauber theory [Bertocchi and Treleani (1977)]. In

fact following the formalism given at page 250, neglecting the correlations in the

nuclear wave function and including, between successive scatterings, all the pos-

sible intermediate states, the inelastic cross section involving m-nucleons for the

production

†

is written as:

(A − m)!m!

hN(inel)

1 − T

hN(inel)

A−m

where σ

hN(inel)

is the inelastic cross-section on nucleon (i.e., ' on proton) [Bertocchi

and Treleani (1977)] and, for a compact notation, the number of nucleons (M

) in a

nucleus is indicated with the atomic weight

A (numerically A ∼ M

). The average

∗

The inelastic collision is treated at page 242.

†

It is assumed that the remaining A − m nucleons only provide inelastic absorption.

As discussed at page 220, to a ﬁrst approximation the atomic weight, A (also referred to as

relative atomic mass, see page 15), of a nuclide is expressed by its mass number.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Nuclear Interactions in Matter 257

numb er of nucleons, participating to the inelastic interaction on nucleus, becomes:

¯ν =

m=1

mσ

!Ã

m=1

−1

hA(inel)

m=1

mA!

(A − m)!m!

hN(inel)

1 − T

hN(inel)

A−m

hN(inel)

hA(inel)

Aσ

hN(inel)

hA(inel)

in which, σ

hA(inel)

is the inelastic cross-section on a nucleus of atomic weight A. Con-

sequently, we have:

¯ν '

A σ

hp(inel)

hA(inel)

, (3.56)

where σ

hp(inel)

is the inelastic cross-section on proton. ¯ν is the average number of

inelastic collisions that the hadron would make with nucleons inside the nucleus if

it remained as a single hadron after each collision. It can be used to express the

average nuclear thickness in units of the mean free inelastic path of the incident

hadron in the nucleus.

For 50 ≤ E

≤ 200 GeV, R

was observed to be approximatively given by [Busza

(1977)]:

≈

¯ν; (3.57)

furthermore, for incoming protons we have ¯ν ≈ 0.70 A

0.31

; while, for incoming pions

¯ν ≈ 0.74 A

0.25

[Busza (1977); Otterlund (1980)].

To account for the absence of an intranuclear cascade, a space-time development

of the hadron–nucleus collision is incorp orated in many theoretical models, such as

the generalized Glauber model by Gribov (1968), the energy ﬂux model by Got-

tfried (1974), the two-phase parton model by Nicolaev (1977), the constituent-quark

model by Bialas (1978), and the coherent-tube model by Dar [Afek et al. (1977)].

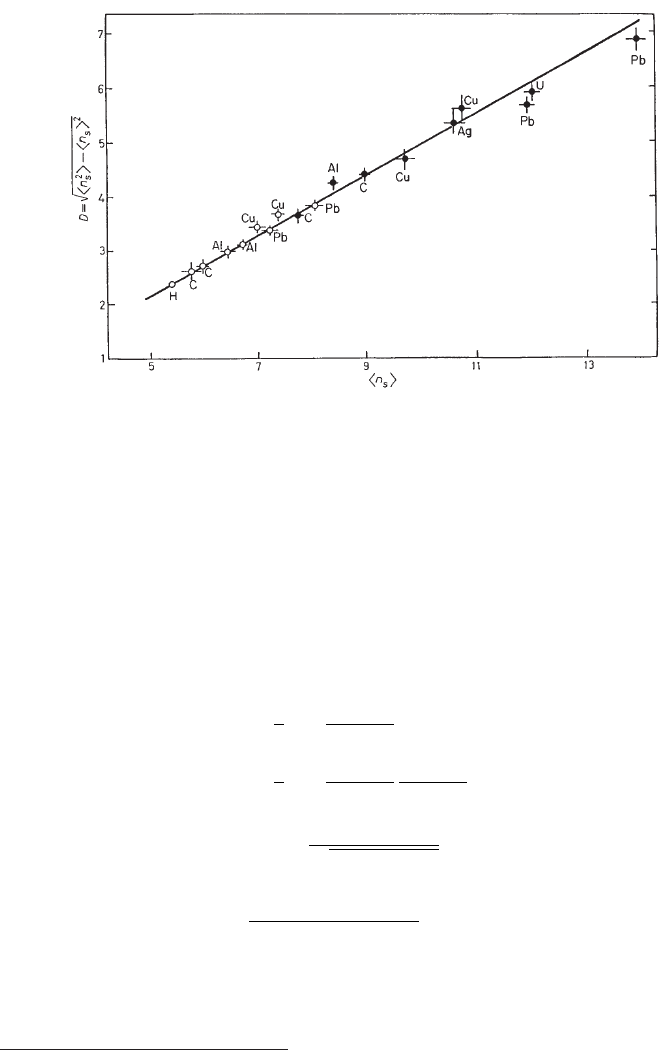
The experimental data on the mean number of shower particles exhibit another

characteristic, i.e., the dispersion, D, which is linearly dependent on the mean

multiplicity, hn

i, of the charged relativistic-particles produced in nuclear intera-

ctions (Fig. 3.15):

D = 0.56 + 0.58 hn

with

D =

i − hn

and n

is multiplicity of the charged relativistic-particles produced in the intera-

ction [Halliwell (1978); Abrasimov et al. (1979)].

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

258 Principles of Radiation Interaction in Matter and Detection

Fig. 3.15 Dispersion D as a function of the mean relativistic charged-particles produced in the

interaction (from [Rancoita and Seidman (1982)], Copyright of the Societ`a Italiana di Fisica). Data

at 50, 100, 200 GeV are from [Halliwell (1978)], while data at 40 GeV are from [Abrasimov et al.

(1979)].

3.2.3.1 Rapidity and Pseudorapidity Distributions

Before discussing the experimental data regarding the angular distributions of se-

condaries produced in interactions on nuclei, let us deﬁne a few variables used to

describe the p–p interactions (e.g. Chapter 4 in [Perkins (1986)]). At high ener-

gies, the longitudinal momentum

distribution of the secondaries produced in p–p

collision was often discussed in terms of the rapidity y, deﬁned as:

y =

E + p

E − p

(3.58)

E + p

E − p

E + p

= ln

E + p

⊥

+ m

, (3.59)

where

E =

+ p

⊥

+ m

, p

⊥

, m

are the energy, the longitudinal momentum (also, referred to as the parallel mo-

mentum), the transverse momentum (also, referred to as perpendicular) and the

rest mass of the produced secondary, respectively. In a collision, the maximum

It is the momentum along the beam direction.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Nuclear Interactions in Matter 259

rapidity-value is reached when the incoming particle is elastically scattered in for-

ward direction (i.e., p

⊥

= 0):

max

= ln

+ p

= ln (γ

+ γ

) , (3.60)

where

= γ

, p

= β

c, m

are the energy, the momentum and the rest mass of the incoming particle, respecti-

vely. Particles having rapidity values close to y

max

are from the so-called projectile

fragmentation region. From Eq. (3.58), in the center-of-mass system, a secondary

with no longitudinal momentum (i.e., p

cm,k

= 0) has y

= 0. In addition, the

relationship between the rapidity minimum, y

cm,min

, and maximum, y

cm,max

, is:

cm,min

= −y

cm,max

In the case of an elastically backward scattered particle, the rapidity is at the

minimum. Furthermore, in the center-of-mass system, the elastic scattering in the

forward direction produces a backward scattered target-particle having opposite

momentum. As a consequence, the forward going particle will be at the rapidity

maximum, while the recoil target-particle will be at the rapidity minimum. Thus,

particles with rapidity values close to the rapidity minimum are from the so-called

target fragmentation region.

Let us determine how the rapidity transforms, under Lorentz transformation,

to another reference frame moving at velocity βc along the longitudinal direction,

i.e., along the incoming particle direction. In the new reference frame, the longitu-

dinal momentum and the energy of the scattered particle are:

c = γ

c − βE

= γ

E − βp

;

while, for the transverse momentum we have

⊥

= p

⊥

Furthermore, from Eq. (3.59) we get:

= ln

+ p

⊥

+ m

= ln

E − βp

+ γ

c − βE

⊥

+ m

= ln

E + p

γ(1 − β)

⊥

+ m

= y + ln [γ(1 − β)]

= y +

(1 − β)

(1 + β)