Leroy C., Rancoita P.-G. Principles Of Radiation Interaction In Matter And Detection

Подождите немного. Документ загружается.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

260 Principles of Radiation Interaction in Matter and Detection

Thus, the rapidity y is simply transformed into the rapidity y

(deﬁned in the

new reference system) by an additive value, determined by β. The particle rapidity

[Eq. (3.59)] can be rewritten as a function of the scattering angle θ and expanded

to obtain:

y =





cos

+ ···

sin

+ ···





(see for instance Section 38.5.2 of [PDB (2008)]); ﬁnally, for p À m

c and θ À 1/γ,

it becomes

y ≈ −ln

¶¸

≡ η, (3.61)

where η is the so-called pseudorapidity.

One important feature of p–p collisions, which were investigated at ISR machine

at CERN, is that the rapidity distribution of secondaries indicates the presence

of a plateau at small center-of-mass rapidity values. It is there that the bulk of

produced particles is concentrated. At large y

(close to y

cm,max

) the distribution

falls rapidly.

Experiments on multiparticle production on nuclei do not usually provide the

momentum measurement of secondaries, but their production angles, i.e., their

peudorapidities, which can be calculated by means of Eq. (3.61). Following the

terminology introduced for the rapidity, particles with low η values are from the

target fragmentation region, while particles with large η values are from the pro-

jectile fragmentation region. The main feature of pseudorapidity distributions for

nuclear targets consists of an excess of multiplicity in the target fragmentation region

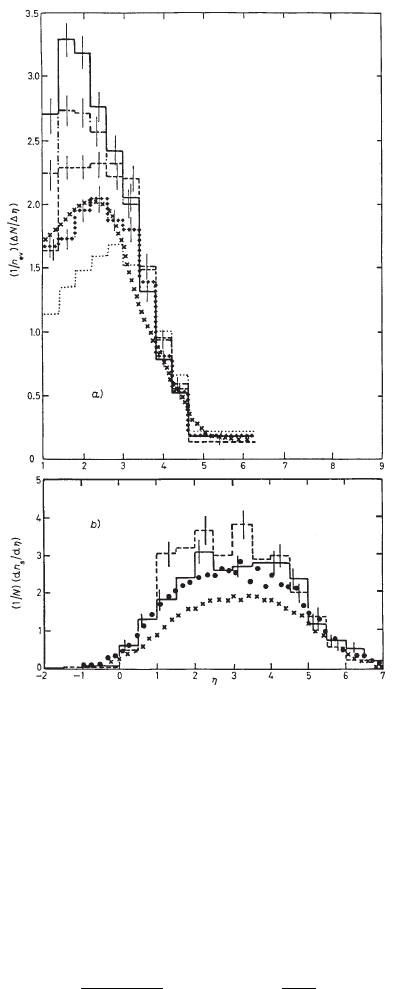
with respect to the pseudorapidity distribution for a proton target (see Fig. 3.16;

the experimental data are from [Abdrakhmanov et al. (1974); Furmanska (1977);

Abrasimov et al. (1979); Faessler et al. (1979); Lee et al. (1979)]). At large angles,

namely in the target fragmentation region, slow secondaries may also come from

nuclear rescattering processes (absent in hadron–proton collisions) [Busza (1977);

Otterlund (1977); Halliwell (1978); Otterlund (1980)]. The average multiplicity in

the forward direction, 3 < η < 4 (i.e., 6

◦

> θ > 2

◦

), is approximately the same as in

hadron–nucleon collisions [Abdrakhmanov et al. (1974); Furmanska (1977); Abrasi-

mov et al. (1979); Faessler et al. (1979); Lee et al. (1979)]. However, in the very

forward direction, η > 4 (i.e., θ < 2

◦

), it becomes lower than the latter one, as it

can be seen in Fig. 3.17, where R(η) is given by:

R(η) =

hA(inel)

dσ

hA(inel)

dη

¸Á·

hN(inel)

dσ

hN(inel)

dη

(3.62)

[Abdrakhmanov et al. (1974); Furmanska (1977); Azimov et al. (1978); Abrasimov

et al. (1979); Faessler et al. (1979); Lee et al. (1979)]. Furthermore, pseudorapidity

distributions are only slightly dependent on A for a ﬁxed topology (the top ology

is the ﬁnal state particle multiplicity), as it can be observed in the experimental

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Nuclear Interactions in Matter 261

Fig. 3.16 a) Pseudorapidity distribution in π–A interaction at 40 GeV (from [Rancoita and Seid-

man (1982)], Copyright of the Societ`a Italiana di Fisica): data on Pb (continous line), Cu (dashed-

dotted line), Al (broken line), C (black lozenge line) are from [Abrasimov et al. (1979)], data on H

(dotted line) are from [Abdrakhmanov et al. (1974)], data on C (crossed line) are from [Faessler et

al. (1979)]. b) Pseudorapidity distribution in π–A interaction at 200 GeV: data on Cr (continuous

line), W (dashed line), and on H (crossed line) are from [Lee et al. (1979)], data on emulsion are

from [Furmanska (1977)]. In the target fragmentation region, the multiplication eﬀect due to the

nucleus is visible.

data shown in Fig. 3.18. These data were collected in a multiparticle production

experiment on nuclei from C to Pb [Abrasimov et al. (1979); Rancoita and Seidman

(1982)]. The global pseudorapidity distribution on a nucleus can be written as:

dσ

hA(inel)

dη

(A)

dσ

dη

where P

(A) is the A-dependent probability for the topology with T -particles in

the ﬁnal state and dσ

/dη is the almost A-independent pseudorapidity distribution

for this topology.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

262 Principles of Radiation Interaction in Matter and Detection

Fig. 3.17 At various energies, the ratio R

[introduced with the symbol R(η) in text, see

Eq. (3.62)] is shown as a function of η for p–emulsion interaction (from [Rancoita and Seid-

man (1982)], Copyright of the Societ`a Italiana di Fisica; see also [Azimov et al. (1978)]). The

continuous line was calculated following the additive quark model prediction [Nikolaev (1977)]. It

can be seen that, in very forward direction (η > 4), the multiplicity in emulsion is lower than the

corresponding one on p-reaction.

3.2.4 Emission of Heavy Prongs

By extending the phenomenological description of shower secondaries produced in

emulsion experiments to other kind of tracks, we observe that shower particles are

usually accompanied by recoiling nucleons (among them, there are quasi-direct pro-

tons), fragments and boiled-oﬀ nucleons emitted by excited nuclear targets. These

nuclear products indicate the presence of spallation processes (see page 267), which

may result in leaving the residual nucleus characterized by diﬀerent atomic weight

and number.

The correlation between the number of relativistic particles (the so-called shower

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Nuclear Interactions in Matter 263

Fig. 3.18 Pseudorapidity distributions at ﬁxed topology in the ﬁnal state for C, Al, Cu, Pb nuclei

(from [Rancoita and Seidman (1982)], Copyright of the Societ`a Italiana di Fisica; see also [Abrasi-

mov et al. (1979)]).

particles, n

, with β > 0.7) and the charged spallation products, namely the

heavy prongs, N

, with β < 0.7, was widely studied using experimental data col-

lected in emulsion experiments. The heavy prongs are subdivided in black and

grey tracks. The grey (black) tracks, N

), are particles with 0.3 ≤ β ≤ 0.7

(β < 0.3). This terminology was adopted from emulsion experiments. The number

of heavy prongs is interpreted as the number of charged fragments and charged

recoiling particles coming from the nuclear target [Otterlund (1977)]. Fast protons

are among the grey tracks, while evaporative protons and nuclear fragments are

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

264 Principles of Radiation Interaction in Matter and Detection

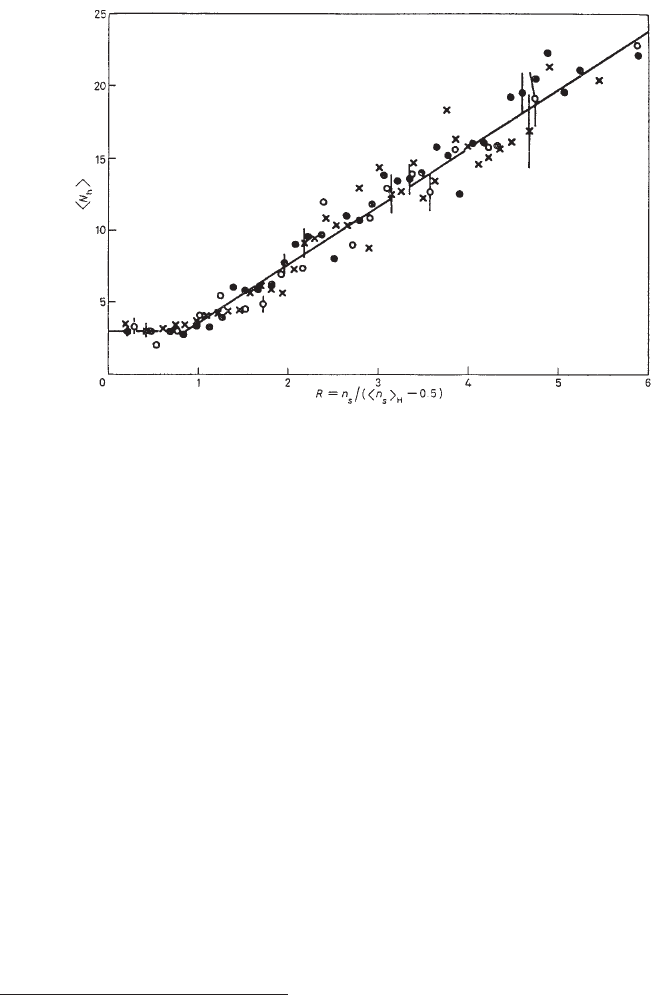
Fig. 3.19 Average heavy prongs hN

i as a function of R for emulsion nuclei (from [Rancoita and

Seidman (1982)], Copyright of the Societ`a Italiana di Fisica). Data at 200 (•), 300 (×) and 400

(◦) GeV are from [Herbert et al. (1974)]. For n

≤ hn

, hN

i is independent of the number of

produced particles.

among the black tracks. Shower particles are also emitted in the backward labora-

tory hemisphere ([Otterlund (1977)] and references therein).

In Fig. 3.19, the average number of produced heavy-prongs

††

is shown as a

function of the parameter R, which is given by n

divided by the energy dependent

term hn

, deﬁned in Eq. (3.55). In Fig. 3.19, hn

is equivalent to the term hn

deﬁned at page 255. The average number of heavy prongs is almost independent

of the number of produced shower particles for n

≤ hn

, with hN

i ' 3. As R

increases, the average number of heavy prongs increases almost linearly. Conversely,

there is a linear dependence of the ratio

†

on the N

value, with a slope almost

independent of the incoming-hadron energy.

Data from p–W, p–emulsion and p–Cr interactions have allowed the conclusion

that the ratio R

(deﬁned at page 255) as a function of N

seems to be inde-

pendent of the nuclear-target mass [Otterlund (1977)]. It was found that hN

i is

almost independent of the incoming-hadron energy, but depends on the target mass

as ≈ A

0.7

. The measured value ([Otterlund (1977)] and references therein) for in-

coherent π(p)-emulsion interactions is ≈ 6.9 (7.7), where the mean atomic weight

of the emulsion nucleus is ' 60. The average number (e.g., see [Azimov (1977)]) of

††

These experimental data were collected in emulsion experiments at 200, 300 and 400 GeV [Her-

bert et al. (1974)].

†

The ratio R

, deﬁned at page 255, is computed without taking into account the number of the

heavy prongs (N

) produced in the interaction. However, it can also be computed as a function

of the number of the heavy-prongs produced in the interaction.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Nuclear Interactions in Matter 265

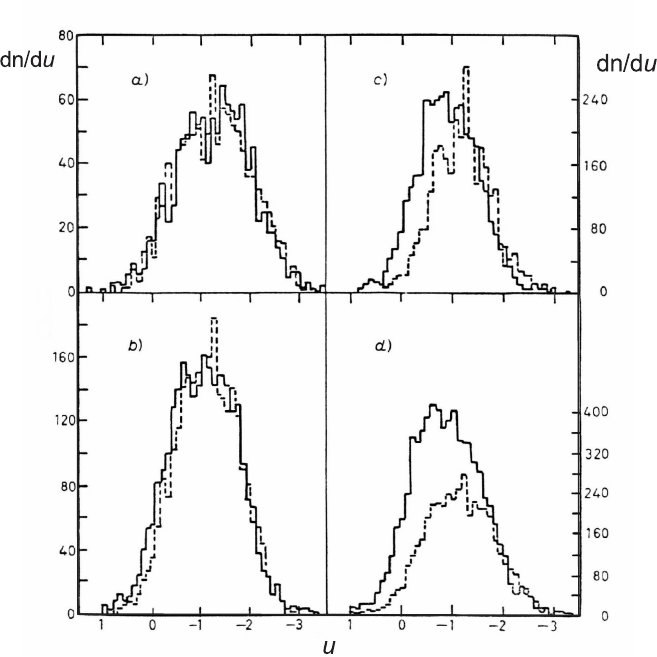
Fig. 3.20 Angular distribution of particles produced in p–emulsion and p–p interactions at

200 GeV as a function of u = −η, where η is the pseudorapidity deﬁned in Eq. (3.61): (a) n

≤ 8,

(b) 9 ≤ n

≤ 16, (c) n

≥ 17, (d) no n

selection (from [Rancoita and Seidman (1982)], Copy-

right of the Societ`a Italiana di Fisica; see also [Alma–Ata–Leningrad–Moscow–Tashkent Collab.

(1974)]). The target fragmentation region in p–emulsion and p–p interactions are quite diﬀerent

for n

≥ 17.

grey (black) tracks for incoming-proton energies b etween 50 and 200 GeV is given

by ' A

0.74

0.66

), while the ratio hN

i/hN

i is ≈ 1.7–1.9. Furthermore, pseudorapi-

dity distributions for p–p and p–emulsion interactions show that the A-dependence

is marked in events with large n

, as it can be seen in Fig. 3.20 for n

≥ 17

from [Alma–Ata–Leningrad–Moscow–Tashkent Collab. (1974)]. The A-dependence

is mostly observed in the target fragmentation region, as already discussed, whereas

a deﬁcit of particles is observed in the projectile fragmentation region.

The frequency of recoil protons with momenta < 1 GeV is rather insensitive to

the incident energy and provides a measurement of the thickness of the nuclear mat-

ter traversed; also, the excitation energy of the residual nucleus varies very little with

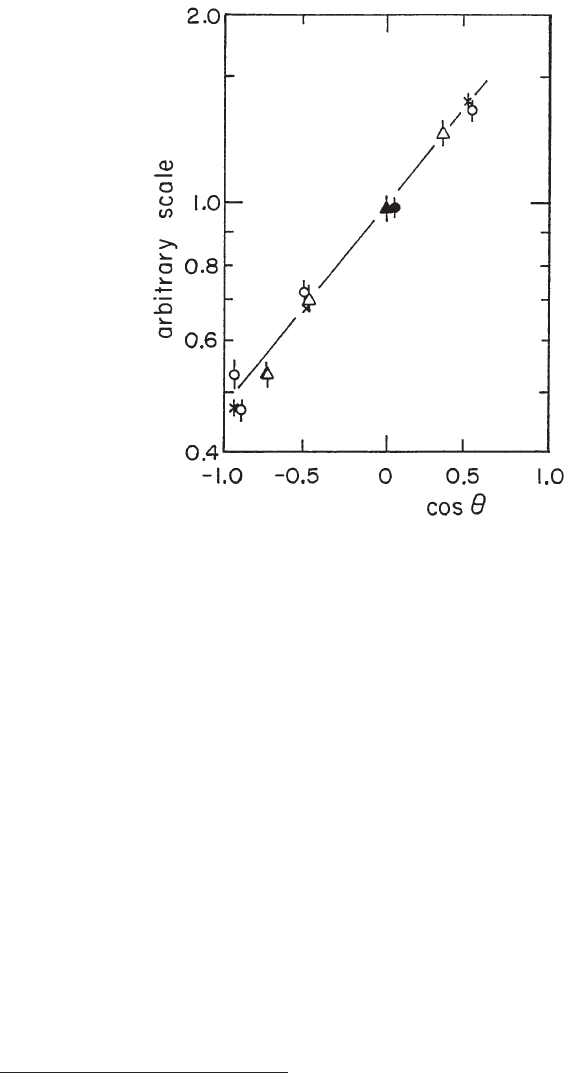
energy. The angular distribution of grey tracks (most of them being fast protons)

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

266 Principles of Radiation Interaction in Matter and Detection

Fig. 3.21 Angular distribution of emitted protons with energies from 60 up to 200 MeV as a

function of the emission angle (θ) in the laboratory: (◦) π–Pb at 1.6 GeV/c, (×) π–Pb at 6.2 GeV/c,

(4) p–Ta at 400 GeV/c; the distributions are normalized at 90

◦

(adapted from Nucl. Phys. A

335, Otterlund, I., High energy reactions on nuclei, 507–516, Copyright (1980), with permission

from Elsevier; see also [Rancoita and Seidman (1982); Leroy and Rancoita (2000)]) .

was measured for recoil protons with energies between 60 and 200 MeV on π–Pb

and p–Ta, and for incoming hadrons with momenta between 1.6 and 400 GeV/c

([Otterlund (1980)] and references therein). It was found (Fig. 3.21) that the distri-

bution has an exp(cos θ) dependence, independently of the incoming-hadron energy

within an accuracy of 5%. These data are in agreement with the measured ratio, in

emulsion experiments, between the emitted grey tracks in the forward hemisphere

and those emitted in the backward hemisphere ([Rancoita and Seidman (1982)] and

references therein). These fast particles, also-called quasi-direct nucleons, are inter-

preted as emitted in gentle (peripheral) collisions through a fragmentation process.

Although, in this section, we have mostly discussed the emission frequency of

charged nucleons (usually protons), the neutron emission probability can be esti-

mated by the proton probability, once the neutron to proton ratio

††

, N

/Z, is taken

into account. For evaporation neutrons, the Coulomb barrier will also aﬀect the

neutron emission probability (Sect. 3.2.6).

††

The ratio varies smoothly with A.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Nuclear Interactions in Matter 267

3.2.5 The Nuclear Spallation Process

The so-called spallation process is a nuclear interaction process in which nucleons

are spalled or knocked-out. This process occurs because the primary interaction on

a quasi-free nucleon inside the nucleus can be followed by secondary interactions of

the struck nucleons with other nucleons. The physical processes inside nuclei seem

to be described by intranuclear cascade models [Bernardini et al. (1952); Segre

(1977)]. Some of the particles taking part in interactions reach the nuclear bound-

aries and, if suﬃciently energetic, can escape. In this step of the spallation process,

most of the emitted charged particles are detected as grey tracks in emulsion ex-

periments. Protons and neutrons will be emitted in a ratio, which corresp onds, on

average, to the N

/Z ratio in the target nucleus, where N

and Z are the num-

ber of neutrons and protons (i.e., the atomic number), respectively. Other particles

remain inside and share their energies with the nucleons inside the nucleus. Physi-

cal processes inside nuclei can lead to the production of highly excited hot nuclei

with subsequent decay modes, like, multifragmentation, vaporization or conven-

tional ﬁssion and evaporation (e.g., [Pochodzalla et al. (1995)]). The further step

of the spallation reaction consists of the de-excitation of the resulting intermediate

nucleus. The excited nucleus decays by ejecting or evaporating nucleons or light

nucleon aggregates, like, deuterons (d), tritium (t), α-particles, etc.; in this step,

most of the emitted charged particles are detected as black tracks in emulsion expe-

riments. In the ﬁnal stage, γ’s can also be emitted. In heavy nuclei, the intermediate

nucleus can ﬁssion, in addition.

Numerous spallation investigations were carried out using many experimental

conditions and, then, attempts to represent the cross sections by a suitable appro-

ximate analytical function were made. An empirical formula was written by Rud-

stam (1966) to reproduce the spallation cross section on a target nucleus of mass

numb er A

and atomic number Z

, but excluding data with heavy ions and pho-

tons as incoming particles. For proton- and neutron-induced reactions and A

> 20,

the simpliﬁed expression for the emission of a spallation product of mass number

and atomic number Z is reduced to [Rudstam (1966)]:

σ(Z, A

) ' F (A

(E)

P exp[−P (A

− A

)]

1 − 0.3/ (P A

)

×exp

−R

|T A

− SA

+ Z|

[mb], (3.63)

where E is the incoming energy, F (A

) (in mb) is the function shown in Fig. 3.22;

(E) ' 1

for energies ' 250 MeV and increases to ≈ 4 at ' 50 MeV,

P ' 20 ×{E[MeV]}

−0.77

, for E ≤ 2100 MeV,

P ' 0.056, for E > 2100 MeV

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

268 Principles of Radiation Interaction in Matter and Detection

Fig. 3.22 Function F (A

) versus the target mass number A

(adapted and reprinted with per-

mission from [Rudstam (1966)]).

and with P A

≥ 1. In addition,

R ' 11.8 A

−0.45

S = 0.486,

T = 0.00038.

The parameter P do es not depend on the type of projectile used, i.e., protons,

neutrons, deuterons, etc. have similar P values.

The total inelastic cross section σ

,inel

for the target nucleus is given by

,inel

Z,A

σ(Z, A

);

while, the average mass number of the spallation products, hA

i, is

i ' A

−

The parameter P is closely related to the ﬁrst stage in the spallation reaction,

namely when intranuclear nucleon cascade interactions are taking place [Rud-

stam (1966)]. At high energy, i.e., for proton interactions on emulsion nuclei at

22.5 GeV [Winzeler (1965)], it was also found a good agreement between the ob-

served average number of protons emitted and the one expected by means of the

parameter P , estimated for the case of charged tracks [Rudstam (1966)]. The para-

meter R is found to be almost independent of both the incoming-particle typ e and

energy. However, it depends on the mass number of the spallation products. The

parameters S and T are related to the peak of the charge distribution.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Nuclear Interactions in Matter 269

An inspection of the cross section formula indicates that, for a given combination

of target and spallation product, the maximum yield is achieved for:

P '

− A

From Eq. (3.63), we get:

σ(Z, A

)

max

≤ F (A

(E)







exp

−1 − R

|T A

− SA

+ Z|

− A

) [1 − 0.3(A

− A

)/A

]







[mb],

where the inequality sign is valid for E ≥ E

Nowadays, systematic investigations on spallation reaction are p erformed in

many laboratories and neutron spallation is used to make neutron sources (see,

for instance, [ESTP (2003)] and references therein).

3.2.6 Nuclear Temperature and Evaporation

During the spallation process, after the primary collision has occurred, fast nucleons

with energies much larger than the binding energy are knocked-out, while other

nucleons with energies lower or comparable to the binding energy can be trapped

inside the nucleus. As a result, the remaining nucleus may be left in an excited

state, from which it mainly decays via an evaporation process. Hence, additional

nucleons or nucleon aggregates (p, n, d, t,

He,

He, . . . ) quit the nucleus; these

emitted particles are among the black tracks observed in emulsion experiments. In

the nucleus rest frame, all emission directions are equally probable. In fact, it is 1.1–

1.2 the measured ratio of black tracks emitted in the forward direction to the ones

emitted in the backward direction [Babecki and Nowak (1979)]: the slight forward

excess observed is due to the motion of the recoiling residual nucleus.

The energy distribution and the relative abundance of evaporated particles can

be estimated by using the continuum theory for nuclear reaction [Weisskopf (1937);

Blatt and Weisskopf (1952)], in which collisions between a particle (or a photon) and

a nucleus are treated by distinguishing two well separated stages. Firstly, we have the

formation of a compound nucleus in a well deﬁned state, in which the received energy

is shared among constituent nucleons. Subsequently, we have the nucleus decay. This

latter stage can be treated independently of the ﬁrst one, i.e., the disintegration

mode of the compound system depends on its energy, angular momentum, and

parity, but not on the speciﬁc way by which it was produced. This two-step process,

in which the nuclear interaction is assumed to occur, is referred to as the Bohr

assumption, whose validity and justiﬁcation are discussed in [Blatt and Weisskopf

(1952)].

To a ﬁrst approximation, the continuum theory allows one to estimate relative

abundances and energy distributions of emitted particles in high energy interactions

on nuclei. In calculations based on this theory, there is no memory of the way in

which the compound nucleus was formed. In the theory, thermodynamical analogies