Leroy C., Rancoita P.-G. Principles Of Radiation Interaction In Matter And Detection

Подождите немного. Документ загружается.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

210 Principles of Radiation Interaction in Matter and Detection

energy. The peripheral part is mainly due to to the propagation of photons. The

spatial distribution of this latter component is determined by the minimum value

of an attenuation coeﬃcient which strongly depends on the absorber medium.

Several two-component parameterizations of the transverse shape of an electro-

magnetic cascade were introduced as a function of the calorimeter depth. Usually,

a double exponential form is employed. This form represents the size of the central

and peripheral cascade components. A ﬁrst example is the parameterization of the

lateral distribution in one direction p erpendicular to the shower axis:

Y (y, t) = a

exp

−

+ a

exp

−

, (2.243)

where y is the distance from the cascade axis and b

, b

are the two lateral attenua-

tion lengths representing the central and peripheral cascade-components, respecti-

vely. From lead-glass data, one ﬁnds [Bianchi et al. (1989)]: b

= (3.4 ± 0.1) mm,

= (9.3 ± 0.3) mm, and a

= 11.9 ± 0.5.

The second example is a parametrization adapted from the one used by the

ALEPH experiment at LEP to simulate the transverse proﬁle of electromagnetic

cascades in a Pb-Scintillating ﬁber calorimeter [Charlot (1992)]. The radial density

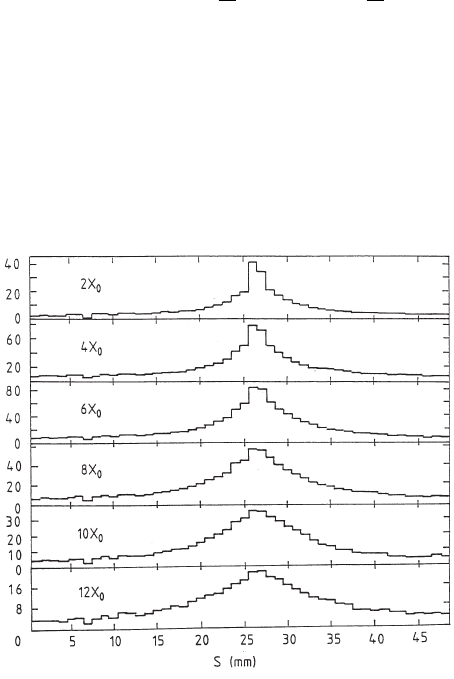
Fig. 2.82 Lateral distribution of the shower for 6 GeV electrons in tungsten absorber up to 12 X

in steps of 2 X

, S being the 1 mm pitch strip number of the readout silicon detector: the di-

stributions shown are from 2 X

(top) up to 12 X

(bottom) (adapted from Nucl. Instr. and

Meth. in Phys. Res. A 279, Lemeilleur, F., Lamarche, F., Leroy, C., Paludetto, R., Pensotti,

S., Rancoita, P.G., Vismara, L. and Seidman, A., Longitudinal and transverse development of

electromagnetic showers using silicon detectors, 66–72, Copyright (1989), with permission from

Elsevier; see also [Leroy and Rancoita (2000)]). The vertical axis is in arbitrary units.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 211

distribution, in polar coordinates, on a plane transverse to the shower axis at a

shower depth t, is given by

F (r, t) = κ

exp

−

+ b(t, E ) exp

−

¶¸

, (2.244)

where κ = µ

(t, E) + b(t, E ) µ

(t, E) and r is the radial distance from the beam

axis expressed in units of X

. The parameters µ

, µ

, and b are functions of the

energy (E) and the depth (t) according to the empirical formulae:

(t, E) = 0.025 exp

(E)

, (2.245)

and

b(t, E) = 0.0003 exp[p

(E) t]; (2.246)

Fig. 2.83 Lateral distribution of the shower for 6 GeV electrons in tungsten and G10 absorbers

up to about 12 X

in steps of about 2 X

, each step consists of 1 X

tungsten followed by 5 mm

G10 (≈ 2.6%X

) followed again by 1 X

of tungsten, S being the 1 mm pitch strip number of the

readout silicon detector (adapted from Nucl. Instr. and Meth. in Phys. Res. A 279, Lemeilleur,

F., Lamarche, F., Leroy, C., Paludetto, R., Pensotti, S., Rancoita, P.G., Vismara, L. and Seidman,

A., Longitudinal and transverse development of electromagnetic showers using silicon detectors,

66–72, Copyright (1989), with permission from Elsevier; see also [Leroy and Rancoita (2000)]). The

vertical axis is in arbitrary units.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

212 Principles of Radiation Interaction in Matter and Detection

is kept constant at all energies and t is in units of radiation length. p

(E)

and p

(E) are ﬁtted to the data by logarithmic functions of the incoming energy

E. This particular parametrization reproduces well the radial proﬁle of cascades up

to energy around 20 GeV, but it has diﬃculty to reproduce the peripheral tail at

higher energy [Charlot (1992)].

A third example is provided by the data obtained from a silicon calorimeter. The

lateral cascade distributions were measured using a silicon calorimeter with W and

U as absorbers for incoming electron energies of 2, 4 and 6 GeV. The experimental

data on lateral distributions were ﬁtted to radial energy-distributions using the

radial-probability density-function

F (r) =

exp

−

√

+ C

exp

−

´i

, (2.247)

where λ

and λ

are attenuation lengths in units of R

, C

is the relative weight

of the two functions and r is the radial distance from the middle of the distribution

(assumed to be the shower axis) in units of R

. N

is a normalizing parameter such

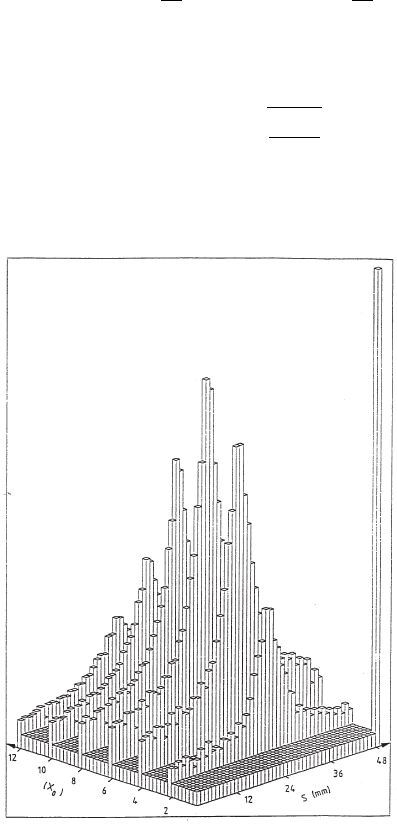
Fig. 2.84 Lateral distribution of the shower for 6 GeV electrons in tungsten and G10 absorbers

up to about 12 X

in steps of about 2 X

, each step consists of 1 X

tungsten followed by 5 mm

G10 (≈ 2.6%X

) followed again by 1 X

of tungsten, S being the 1 mm pitch strip number of

the readout silicon detector: the distributions shown are from 2 X

(top) up to 12 X

(bottom)

(adapted from Nucl. Instr. and Meth. in Phys. Res. A 279, Lemeilleur, F., Lamarche, F.,

Leroy, C., Paludetto, R., Pensotti, S., Rancoita, P.G., Vismara, L. and Seidman, A., Longitudinal

and transverse development of electromagnetic showers using silicon detectors, 66–72, Copyright

(1989), with permission from Elsevier; see also [Leroy and Rancoita (2000)]). The vertical axis is

in arbitrary units.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 213

that

2π

dφ

+∞

F (r) r dr = 1, (2.248)

where φ is the polar angle. Alternatively, the normalization can be chosen in

such a way to reproduce the longitudinal energy proﬁle of the shower. It was ob-

served [SICAPO Collab. (1988a)] that the values of λ

are proportional to the

calorimeter depth, t, with a slope proportional to

√

(E is the incoming energy in

GeV) and are similar for both U and W absorbers. Furthermore, it was found that

the values of λ

and C

are almost independent of t and E for both W and U ab-

sorbers and scale approximately with R

. The t-dependence of λ

can be explained

by the fact that in the electromagnetic-cascade development the energy is mainly

carried by relativistic electrons and positrons for small t-values, but mainly by soft

electrons, positrons and photons (which are also present at small depths but not

dominant) at large t-values. The fast electrons and positrons are able to penetrate

more and more inside the calorimeter as the energy increases. This relates the para-

meter λ

to the incoming energy E. The lateral energy distribution of the cascade

broadens with increasing absorber depth, although most of the energy is deposited

in the central cascade region for depths t < 6 [SICAPO Collab. (1988a)]. The

two-comp onent structure can take into account the fact that cascades develop i) a

narrow central part containing most of the incident energy corresponding to energy

deposition by fast electrons and ii) a broad lateral part due to photons and slow

electrons scattered away from the cascade axis. It has to be noted that a linear

sum of two Bessel functions of diﬀerent slopes was considered [SICAPO Collab.

(1991a)]. The ﬁt to the data is rather good, but the four parameters, thus obtained,

are diﬃcult to interpret physically.

The following ansatz was also used [Grindhammer et al. (1990)]: the radial

energy proﬁle of the electromagnetic cascade is represented by the function

f(r) =

2 rR

+ R

)

, (2.249)

where r, the radial distance from the shower axis, and the free parameter R are in

units of R

. This parametrization holds, at least, as long the lateral resolution of

the calorimeter is of the order or larger than ≈ 1R

. The parameter R also depends

on the calorimeter depth t and on ln E (E in GeV). A reasonable agreement between

this model and experimental data is achieved in the description of the core and halo

of cascades.

2.4.2.4 Energy Deposition in Electromagnetic Cascades

In electromagnetic cascades, the energy is propagated, both laterally and longi-

tudinally, by an increase in the number of electrons and photons of diminishing

energy.

The ionization and excitation processes which precede the energy deposition by

collision losses of electrons and positrons were investigated using EGS4 Monte-Carlo

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

214 Principles of Radiation Interaction in Matter and Detection

simulations [Nelson, Hirayama and Rogers (1985)]. The rate of energy deposition

depends on the Z-value (Z

absorber

) of the medium, as expected. At the incoming

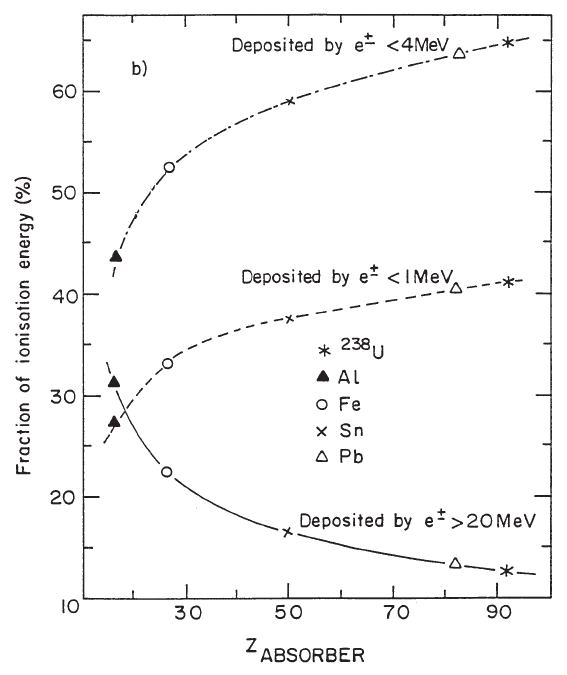
electron energy of 10 GeV [Wigmans (1987)], the simulations indicate that more

than 65% of the energy is deposited by collision losses of particles with energy lower

than 4 MeV and only ≈ 12% with energy larger than 20 MeV in high-Z materials

(like uranium or lead). In low-Z materials (like aluminium), these fractions become

≈ 43 and 32%, respectively. In Fig. 2.85, results of EGS4 simulations from [Wigmans

(1987)] are shown for Al, Fe, Sn, Pb and U absorbers. The fraction fr of the energy

deposited by particles with energy larger than 20 MeV is approximately represented,

in percentage, by

fr(> 20 MeV) = −9.3 ln(Z

absorber

) + 54.5, (2.250)

while the fraction of the energy deposited by particles with energy lower than 4 MeV

fr(< 4 MeV) = 10.5 ln(Z

absorber

) + 17.4, (2.251)

which becomes for particles with energy lower than 1 MeV

fr(< 1 MeV) = 5.0 ln(Z

absorber

) + 17.0. (2.252)

The sum of the two fractions, for energies larger than 20 MeV and smaller than

4 MeV, amounts to ≈ 76% and is almost independent of the medium.

The electron and positron angular spread was investigated by Monte-Carlo simu-

lations [Fisher (1978); Amaldi (1981)]. The charged particles are expected to spread

laterally because of multiple Coulomb, Compton and photoelectric interactions, as

previously discussed. The size of this spread depends on R

. The mean co-

sine value of the charged-particle opening angle, θ (in radian), was evaluated by

Amaldi (1981) and it is given by

hcos θi ≈ cos

π²

, (2.253)

where E

= 21.2 MeV and ²

is the critical energy.

2.4.3 Shower Propagation and Diﬀusion in Complex Absorbers

Rossi’s analytical formulation of shower transport does not address the problem of

shower propagation within a complex medium. By complex medium is meant, in the

case of a calorimetric device, a structure subdivided regularly in passive samplers,

readout by active media located after each of them. A passive sampler is composed

of several absorbers, none of them having its thickness negligible in units of radiation

length. Therefore, the shower cannot be considered as generated in a single type of

absorber, and its basic characteristics (like the shower maximum depth) cannot be

simply related to a well determined critical-energy value.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 215

Fig. 2.85 Fraction of the energy of a 10 GeV electron shower that is deposited through ionization

by electrons and positrons with energies lower than 1 or 4 MeV or larger than 20 MeV, as a function

of the atomic number (Z

absorber

) of the calorimeter absorber (reprinted from Nucl. Instr. and

Meth. in Phys. Res. A 259, Wigmans, R., On the energy resolution of uranium and other

hadron calorimeters, 389–429, Copyright (1987), with permission from Elsevier; see also [Leroy

and Rancoita (2000)]).

As discussed in previous sections, low-energy photons lead to the generation of

low-energy electrons by Compton and photoelectric eﬀects, which have a diﬀerent Z-

dependence, i.e., the Compton cross section is proportional to Z and the photoelec-

tric cross section has a dependence close to Z

. The Z-dependence largely accounts

for the diﬀerential attenuation of radiation in absorbers. Most of these generated

low-energy electrons are absorbed before they reach the readout medium. In gene-

ral, thicknesses not small compared with the material radiation-length are needed

for absorbing soft electrons and positrons with energy below or close to the critical

energy: as previously seen, their dE/dx by collision loss is ≈ ²

. Thus, a signif-

icant change in the soft-energy deposition can be expected if materials with large

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

216 Principles of Radiation Interaction in Matter and Detection

diﬀerence among their critical-energy values

‡

are sequentially set in the complex

passive-sampler. Results of EGS4 Monte-Carlo simulations (Fig. 2.85) are summa-

rized in Eq. (2.250) and Eq. (2.251) for showers generated in a single absorber. As

mentioned in Sect. 2.4.2.4, these equations indicate that for large-Z

absorber

(like

W, Pb and U) more than 65% of the energy is deposited by particles with energy

lower than 4 MeV, while ≈ 12% is deposited by particles with energy larger than

20 MeV. These fractions become lower than 50% and ≈ (30–20)%, respectively, for

low-Z absorbers (like

Al and Fe).

When cascading particles are traversing materials with large diﬀerences in their

critical energies, there is a change in the energy deposition per g/cm

resulting

from collision and radiative energy-losses. In fact, low-Z (high-Z) materials have

large (small) critical-energies. In addition, the stopping power by collision loss and

the mass attenuation length per g/cm

are larger in low-Z media than in high-Z

media. The energy deposition-rate changes because the shower, composed of charged

particles and photons generated in a medium, deposits its energy according to the

stopping power and attenuation length of another material. As an example, when

a cascade initiated in a high-Z material enters a low-Z absorber, electrons and

positrons with energies between 20 and 7 MeV will lose energy predominantly by

collision, while traveling in the high-Z absorber the loss of energy will be largely by

radiation. Furthermore, the rate of low-energy photon interactions by photoelectric

eﬀect is reduced. If the absorber sequence is reversed, the electrons and positrons

with energies between 20 and 7 MeV will reverse the way they are losing energy,

and low-energy photons will be more absorbed in high-Z materials.

It can be concluded that the process of shower transport and energy deposition

depends on the complex absorber-structure and it is also aﬀected by the sequence of

employed absorbers.

‡

This corresponds to a large diﬀerence in the atomic numbers (Z

absorber

) of absorbers.

The critical energies of these absorbers are between about 7 and 8 MeV.

The critical energies of these absorbers are about 40 and 21 MeV, respectively.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Chapter 3

Nuclear Interactions in Matter

In the previous chapter, we discussed the electromagnetic interactions of elec-

trons, positrons, photons and heavy charged-particles with matter. These intera-

ctions manifest themselves in many ways, like ionization or excitation of atoms or

molecules; they can also result in i) emission of photons or electrons, ii) emission

of radiation due to a collective eﬀect in the dielectric medium, iii) electron and

positron pair generation and, ﬁnally, iv) bremsstrahlung.

On the other hand, there are processes induced by hadronic particles or hadrons,

which are responsible for nuclear and subnuclear interactions, also called strong

interactions. Although some hadronic interactions were already considered, like for

instance the hadronic feature of photon interactions on nuclei, a general and detailed

description of strong interactions is beyond the purpose of this book.

In the present chapter, hadronic interactions will be addressed from a phe-

nomenological point of view, at energies large enough to be outside the ﬁeld of

nuclear physics. In particular, the hadron–nucleus interaction will be discussed in

the third section; it is the fundamental phenomenon for the development and propa-

gation of hadronic showers in matter (see, also, the chapter on Principles of Particle

Energy Determination). Low energy reactions are only mentioned: they are treated,

with more details, in specialized nuclear physics textbooks. As an introduction to

hadron–nucleus collisions, we will shortly review general properties of nuclei in the

ﬁrst section; while, in the second section, the phenomenology of hadron–nucleus

collisions is treated at high energy. Furthermore, complete data sets regarding nu-

clear and nuclide properties, discussed within this chapter, are available on the web

(see, for instance, [NNDC (2008a,b)]).

3.1 General Properties of the Nucleus

The nucleus is the inner constituent of the atom, which is the basic element of

matter. A nucleus is a system of M

elementary particles, namely protons and

neutrons, held together by attractive nuclear forces which can be treated, to a good

approximation, by methods of non-relativistic quantum-mechanics. M

is called

217

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

218 Principles of Radiation Interaction in Matter and Detection

mass number (or atomic mass-number ) and is the sum of the total number of

protons, also referred to as atomic number Z, and neutrons (N

) inside the nucleus,

i.e.,

= Z + N

. (3.1)

Nowadays, we know that the nuclear force is not a fundamental force and that it

results from strong interactions which are gluing quarks together, thus, generating

the individual protons and neutrons. These particles are also referred to as nucleons,

when inside a nucleus. The strong interaction also maintains protons and neutrons

together overcoming the repulsive electrostatic force among protons. Therefore, M

is the number of nucleons inside the nucleus.

Diﬀerent combinations of

and

are called

nuclides

. Nuclides with the same

mass number are called isobars. Nuclides with the same Z-value are called isotopes

(see Appendix A.5). Nuclides with the same value of N

are called isotones. Fur-

thermore, we will follow the traditional nuclear physics notation for nuclides. Thus,

for an element whose chemical symbol is X, the corresponding mass, atomic and

neutron numbers are indicated as:

Often, both the atomic and neutron numbers are not explicitly shown. For instance,

the carbon isotope with mass number M

= 14 can be written equivalently as:

C or, simply,

The nucleus can be found in series of quantum states of diﬀerent energy. The

state of lowest energy, the so-called ground state, is the state into which the nucleus

returns after the emission of one or several photons, after having been excited.

The amount of nuclear binding energy indicates the degree of the nucleus sta-

bility. This energy, E

, is related to the mass diﬀerence 4M between the system

(nucleus) mass and the sum of the masses of its constituents. This phenomenon

was historically called mass defect and, following the mass energy equivalence, it is

expressed as:

= 4M c

. (3.2)

The mass of the nucleus is given by:

Nuc

= Zm

+ (M

− Z) m

− 4M, (3.3)

where m

and m

are the proton and neutron rest-masses, respectively. Since the

whole atom is neutral, the number of electrons is equal to the number of pro-

tons. The nuclear binding energy is determined from the atomic masses, M

, be-

cause they can be measured with a larger precision than nuclear masses [Andi and

Wapstra (1993)]. By neglecting the binding energies of the electrons, the atomic

mass diﬀers from the nuclear mass (M

Nuc

) by the the rest-masses of the electrons,

i.e.,

= Zm + M

Nuc

, (3.4)

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Nuclear Interactions in Matter 219

where m is the electron rest-mass. From Eqs. (3.3, 3.4), we have:

= [ZM

+ (M

− Z) m

− M

] c

≈ [Z(m

+ m) + (M

− Z) m

− Zm − M

Nuc

] c

= 4Mc

, (3.5)

where M

is the mass of the hydrogen atom, whose binding energy is 13.6 eV and

can be neglected. The atomic mass is most often expressed in uniﬁed atomic mass

units (u). In those units, the mass of the hydrogen atom is M

' 1.00794 u. As

discussed in Sect. 1.4.1, the uniﬁed atomic mass unit is equal to 1/12 of the

atomic mass in its ground state. The values of the atomic masses of isotopes are

perio dically reviewed to account for the latest measurements and are also available

on the web (e.g., see [Tuli (2000); NNDC (2003); IUPAC (2006); NNDC (2008a)]).

The binding energy per nucleon E

is shown in Fig. 3.1 ([Povh, Rith,

Scholz and Zetsche (1995)] and references therein; see also [Marmier and Sheldon

(1969)]). For most nuclei (all but the very light

∗

ones below M

= 11), the value of

the average binding energy per nucleon of an isotope (I), i.e.,

nucl

(I, M

) =

(I, M

)

4M(I, M

) c

, (3.6)

slightly varies around (7.0–8.8) MeV/nucleon.

In practical calculations in which i) the mass diﬀerence between proton and

neutron can be neglected, i.e.,

nucl

' m

where m

nucl

is the nucleon mass, ii) the dependence of the binding energy on M

can

be neglected, i.e., B

nucl

(I, M

) is replaced by an almost constant eﬀective value B

and iii) the contribution of electrons to the overall mass is not taken into account,

the atomic mass of a nuclide, with atomic number Z and N

neutrons, is obtained

using Eqs. (3.2, 3.4, 3.6), which allow one to approximate Eq. (3.3) as:

≈ M

Nuc

≈ M

nucl

1 −

nucl

(3.7)

= M

nucl

1 −

nucl

(I, M

)

nucl

(3.8)

' M

nucl

1 −

nucl

. (3.9)

Under these assumptions, from Eq. (3.9) the atomic mass of

C is:

at,

= 12 u ≈ M

Nuc,

∼ 12 m

nucl

1 −

nucl

;

thus, one ﬁnds

u ≈ m

nucl

1 −

nucl

(3.10)

∗

For

C, the value of the binding energy per nucleon is B

nucl

(

C, M

) ≈ 7.7 MeV/nucleon; for

He,

Li,

Be and

B are ≈ 7.1, 5.6, 6.5 and 6.5 MeV/nucleon, respectively.