Leroy C., Rancoita P.-G. Principles Of Radiation Interaction In Matter And Detection

Подождите немного. Документ загружается.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

150 Principles of Radiation Interaction in Matter and Detection

2.3.2.1 The Klein–Nishina Equation for Unpolarized Photons

The cross section for Compton scattering on quasi-free electrons was ﬁrst deduced by

Klein and Nishina (1929). For present purposes, we will limit ourselves to a summary

of the theoretical equations for unp olarized photons. Details of the treatment for

both polarized and unpolarized incoming photons can be found in the original paper

and in [Heitler (1954)].

The diﬀerential cross section for Compton scattering of an unpolarized photon

interacting on a quasi-free electron is given by the so-called Klein–Nishina equation:

dσ

dΩ

C,e

− sin

[cm

−1

/electron]. (2.179)

Since in the Compton scattering the ratio

hν

is given by means of Eq. (2.174),

we can rewrite Eq. (2.179) as:

dσ

dΩ

C,e

1 + E (1 − cos θ

)

½·

1 + E (1 − cos θ

)

+ 1 +

−

cos

)

−

sin

1 + E (1 − cos θ

)

1 + [1 + E(1 − cos θ

)]

E − E cos θ

+ cos

¢ª

[1 + E (1 − cos θ

)]

−E cos

+ (1 + cos

)(E

+ E + 1) − E cos θ

(2 E + 1)

(2.180)

in units of cm

−1

/electron. Sometimes, Eq. (2.180) can be written equivalently

(in units of cm

−1

/electron) as:

dσ

dΩ

C,e

1 + cos

[1 + E (1 − cos θ

)]

1 +

(1 − cos θ

)

(1 + cos

) [1 + E (1 − cos θ

)]

. (2.181)

For low energies, i.e., for E → 0 [when we expect hν

≈ hν independently of the angle

of the scattered photon, see Eq. (2.174)], the diﬀerential Compton cross section

expressed in Eq. (2.181) approaches the so-called classical Thomson diﬀerential

cross section (derived in Sect. 2.3.2.3):

dσ

dΩ

C,e

→

dσ

dΩ

T h,e

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 151

where

dσ

dΩ

T h,e

(1 + cos

) [cm

−1

/electron]. (2.182)

Furthermore, in the forward direction for θ

→ 0

◦

, i.e., when the energy of the

scattered photon is hν

≈ hν, independently of the incoming photon energy [see

Eq. (2.174)], the diﬀerential Compton cross section approaches a constant value:

dσ

dΩ

C,e

→ r

[cm

−1

/electron].

For θ

→ 180

◦

, i.e., when photons are scattered backwards, the diﬀerential Compton

cross section becomes:

dσ

dΩ

C,e

→ r

(2 E

+ 2 E + 1)

(1 + 2 E)

[cm

−1

/electron].

Thus, for E À 0, the diﬀerential cross section for backward scattered photon de-

creases as 1/E as E increases. The Klein–Nishina diﬀerential cross section on free

electrons is shown in Fig. 2.53, as a function of the reduced photon energy.

The energy distribution of the scattered radiation can be obtained by introducing

the expression (2.175) in Eq. (2.179) and integrating over the azimuthal angle φ:

2π

dσ

dΩ

C,e

dφ

dσ

d cos θ

C,e

= πr

hν

(

hν

− 1 +

1 −

hν

− 1

¶¸

)

= πr

hν

(

1 +

hν

1 + 2 E

hν

− 2

(1 + E)

)

Since

dσ

d cos θ

C,e

= E

(hν

)

hν

dσ

d(hν

)

C,e

we obtain, in units of cm

MeV

−1

/electron:

dσ

d(hν

)

C,e

πr

hν

(

hν

1 + 2 E

hν

−2

(1 + E)

)

, (2.183)

where hν

is in units of MeV and varies between [Eq. (2.174)]

hν

1 + 2 E

≤ hν

≤ hν.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

152 Principles of Radiation Interaction in Matter and Detection

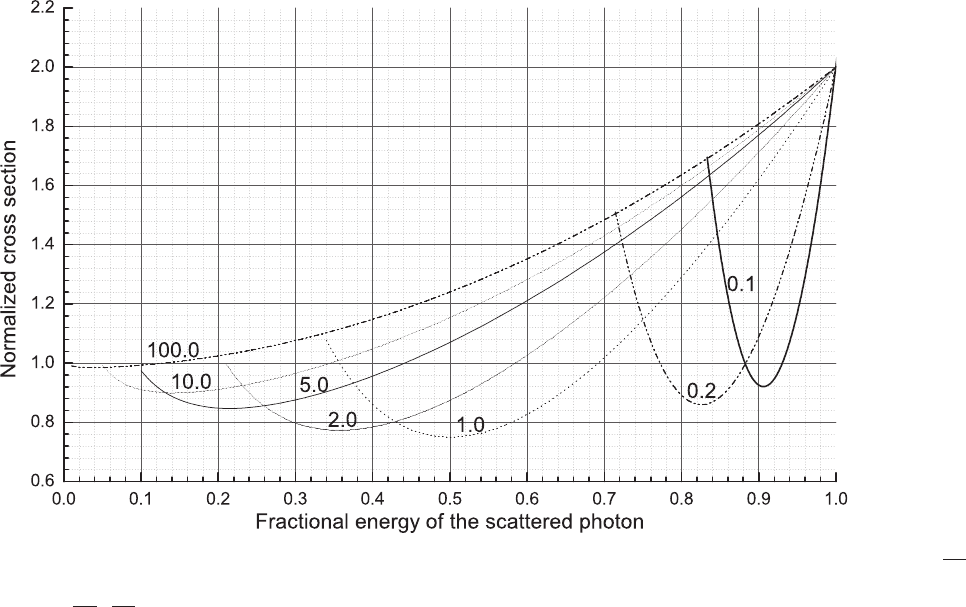
Fig. 2.54 Compton energy distribution of the scattered photon on free electrons as a function of the fractional scattered photon energy

hν

calculated by means of Eq. (2.183) for reduced energies E = 0.1, 0.2, 1.0, 2.0, 5.0, 10.0, and 100.0. In ordinate, the cross section from Eq. (2.183)

is shown once divided by

πr

hν

, i.e., it is the term in brackets in Eq. (2.183).

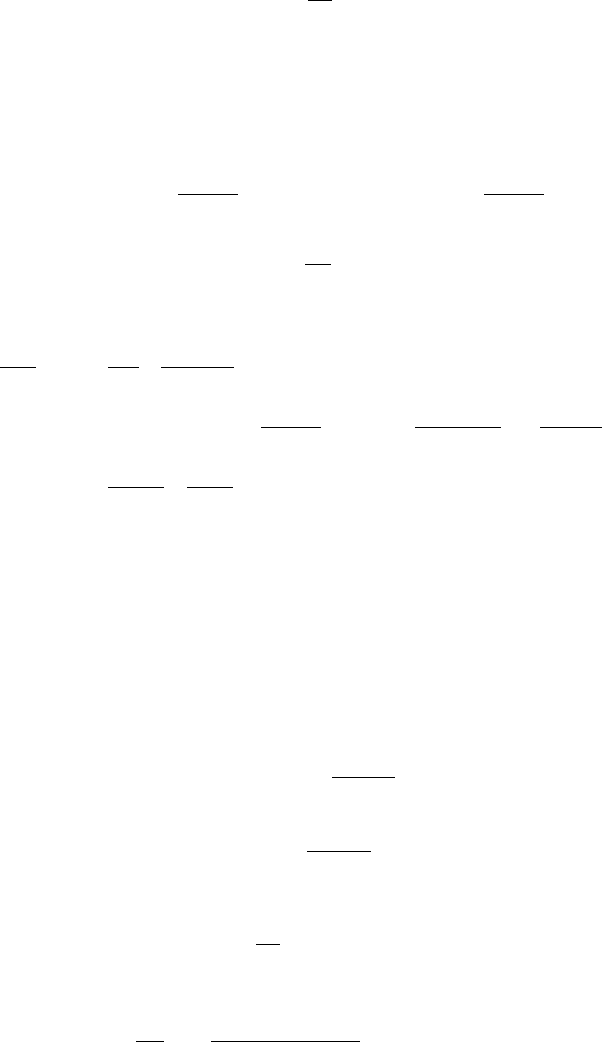
January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 153

The term in brackets in Eq. (2.183) is shown in Fig. 2.54. For small values of E,

there is a limited spread for the fraction

hν

, but a drop of the cross section to a

minimum followed by a rise at the lower end of the spectrum. As E increases, the

rise following the minimum gradually decreases.

In the scattering on free electrons, the kinetic energy (K

) of the recoil electron

is obtained by means of Eq. (2.169). Thus, Eq. (2.183) also expresses the diﬀerential

cross-section for an electron to be scattered with recoil energy hν−hν

. By inspecting

the range of hν

, we get that the kinetic energy of the recoil electron varies between

0 ≤ K

≤ 2 hν

1 + 2 E

, or, equivalently, 0 ≤ η

≤

2 E

1 + 2 E

where

hν

. (2.184)

Furthermore, Eq. 2.183 can be rewritten in terms of K

and η

(in units of

MeV

−1

/electron) as:

dσ

C,e

πr

hν − K

1 + (1−η

)

1 + 2 E

(1−η

) +

(1−η

)

− 2

(1 + E)

πr

1−η

K(E, K

), (2.185)

where the function K(E, K

) is given by

K(E, K

) =

1 + (1−η

)

(1−η

) + (1 + 2 E) (1−η

)

+1 − 2 (1 + E) (1−η

)

(2−2η

+2η

) − η

(1+2E) − 1

(1−η

) + 1. (2.186)

In Fig. 2.55, it is shown the diﬀerential cross-section, calculated by means of

Eq. (2.185) and multiplied by E, in units of b/MeV for E = 0.1, 0.2, 1, 2, 2.45,

5, 10 and 100. E = 2.45 corresp onds to the average energy of photons emitted from

Co source. By an inspection of this latter ﬁgure, at the energy value

e,edge

= 2 hν

1 + 2 E

or, equivalently,

e,edge

2 E

1 + 2 E

there is sharp decrease of the diﬀerential cross-section, which increases with increas-

ing photon energy. K

e,edge

is referred to as Compton-edge

The average fractional energy

hν

decreases as the photon energy increases

and it is given by the approximate formula (see Equation (107) in Part II Section 3B

of [Bethe and Ashkin (1953)]):

hν

(4/3) − 3/(2 E)

ln (2 E + 1) + 1/2

, for E À 1.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

154 Principles of Radiation Interaction in Matter and Detection

Fig. 2.55 Compton diﬀerential cross-sections on a free electron [Eq. (2.185)] multiplied by E as a function of the kinetic energy divided by the

incoming photon energy [η

, see Eq. (2.184)]. The curves are for E = 0.1, 0.2, 1, 2, 2.45 (i.e., it corresponds to the average energy of photons from a

Co source), 5.10 and 100.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 155

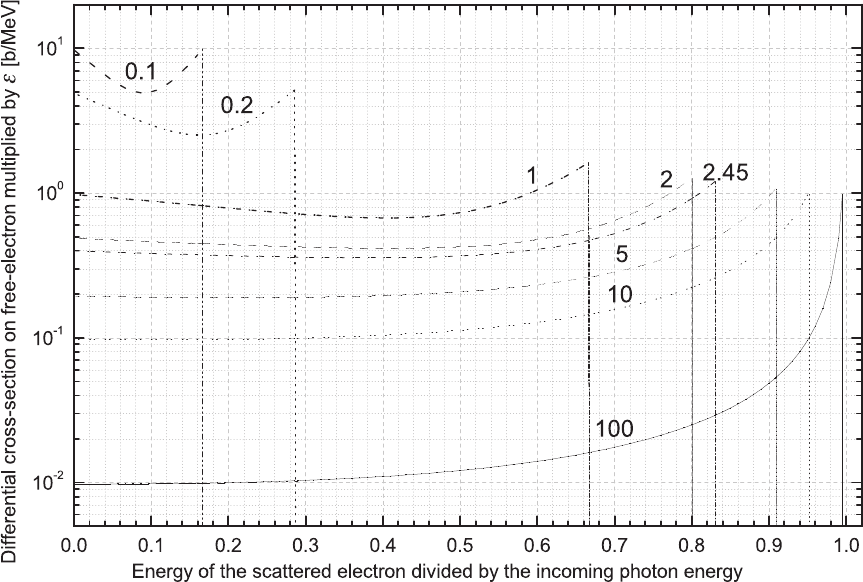
Fig. 2.56 Compton cross sections on a free electron: total [computed by means of Eq. (2.188],

energy absorption [computed by means of Eq. (2.189)] and energy scattering in units of the Thom-

son cross section σ

T h

and as functions of the incoming photon energy in MeV.

The total Compton cross section can b e derived in units of cm

/electron by

integrating Eq. (2.183) over the scattered photon energy:

C,e

hν

hν/(1+2 E)

dσ

d(hν

)

C,e

d(hν

)

πr

ln (1 + 2 E)

1 − 2

(1 + E)

−

2(1 + 2 E)

= σ

T h

8 E

ln (1 + 2 E)

1 − 2

(1 + E)

−

2(1 + 2 E)

, (2.187)

where σ

T h

is the classical Thomson cross section. Equation (2.187) can be rewritten

in units of cm

/electron in an equivalent way as:

C,e

= 2 πr

½·

1+E

¸·

(1+E)

1 + 2 E

−

ln(1+2 E)

2 E

−

1 + 3 E

(1+2 E)

. (2.188)

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

156 Principles of Radiation Interaction in Matter and Detection

For E ¿ 1, this equation can be expanded

∗

as:

C,e

= σ

T h

1 − 2 E +

···

[cm

/electron]

C,e

T h

(1 + E)

1 + 2 E +

−

− ···

[cm

/electron],

which become for E → 0:

C,e

→ σ

T h

πr

[cm

/electron].

For E À 1, Eq. (2.187) can be written as:

C,e

→ σ

T h

8 E

ln (2 E) +

T h

[2 ln (2 E) + 1]

[cm

/electron].

Thus, the total Compton cross section decreases as the primary photon energy in-

creases. It has to be noted that Eq. (2.188) refers to the total cross section for

Compton interaction on a free electron. However, the energy taken by recoil elec-

trons is lower than the energy hν removed by the incoming photons. The energy

transferred to the recoiling electron is given by hν

1 −

hν

, where

hν

is the

fraction of the primary photon energy carried by the scattered photon. Usually,

this energy is absorbed in the medium, following the collision loss process of the

low energy recoiling electron; thus, it is the part of the primary-photon energy de-

posited in matter after a Compton interaction. The probability, for the recoil kinetic

energy K

[Eq. (2.169)] to be imparted to the electron in a Compton collision, can

be evaluated in terms of the so-called energy absorption cross section, σ

C,e,a

, by

integrating the energy distribution of the scattered electron [Eq. (2.183)] weighted

by the fractional energy carried by electrons

1 −

hν

C,e,a

hν

hν/(1+2E)

1 −

hν

¶·

dσ

d(hν

)

C,e

d(hν

)

= 2 πr

3 + 11 E + 9 E

− E

(1 + 2 E)

−

4 E

3(1 + 2 E)

−2πr

3 + 2 E − E

2 E

ln(1 + 2 E) [cm

/electron], (2.189)

where 2 πr

T h

. The corresponding scattered-energy cross section, σ

C,e,s

, i.e.,

that one which corresponds to the energy carried by scattered photons, is given by

C,e,s

= σ

C,e

− σ

C,e,a

C,e,s

is referred to as the energy scattering cross section.

∗

The reader can see i) for the ﬁrst approximate expression Equation (46), in Section 22 of

Chapter V in [Heitler (1954)] and ii) for the second Equation (2.-9) in [Hubbell (1969)], where

additional terms of the expansion can also be found.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 157

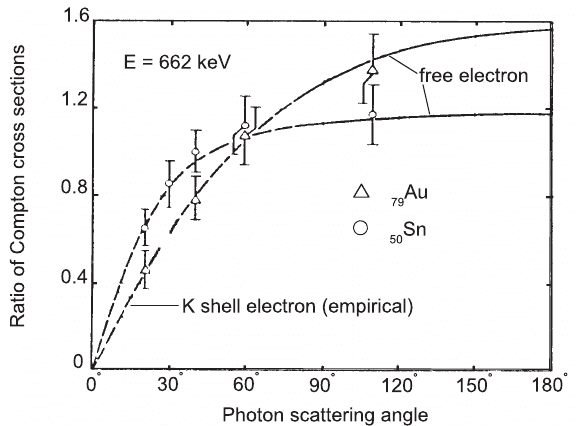
Fig. 2.57 Ratio of the observed Compton scattering from K-shell electrons to Klein–Nishina

theory as a function of the angle of the scattered photon (adapted and republished with p ermission

from Motz, J.W. and Missoni, G., Phys. Rev. 124, 1458 (1961); Copyright (1961) by the American

Physical Society).

The total [computed by means of Eq. (2.188)], energy scattering and energy

absorption [computed by means of Eq. (2.189)] Compton cross sections are shown

in Fig. 2.56 for incoming photon energies between 0.01 and 10 MeV. The cross

sections are in units of Thomson cross section, i.e., they were divided by σ

T h

. As

the photon energy increases, the energy scattering cross section becomes less and

less important with respect to that for energy absorption. On the other hand, the

energy scattering part of the total cross section is dominant at lower photon energies,

i.e., below ≈ 1 MeV.

2.3.2.2 Electron Binding Corrections to Compton and Rayleigh Scatterings

In the treatment of γ-ray transport, electron binding eﬀects were often ne-

glected. The reason being that for low-Z materials K-shell binding energies are low

with respect to the photon energies considered, while for high-Z materials (with

larger K-shell binding energies) K-shell electrons are a small fraction of the total.

Experimental data indicate a departure from the Klein–Nishina angular distribu-

tion [Eq. (2.179)] at low energy photon scattering. Figure 2.57 shows, for Sn and Au,

the ratio of the observed diﬀerential cross sections on K-shell electrons by 0.662 MeV

photons [Motz and Missoni (1961)] to those calculated from Eq. (2.179). At small

scattering angles, the eﬀect of binding energies results in the decrease of the distri-

bution, on the contrary at large scattering angles an increase occurs. Nevertheless,

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

158 Principles of Radiation Interaction in Matter and Detection

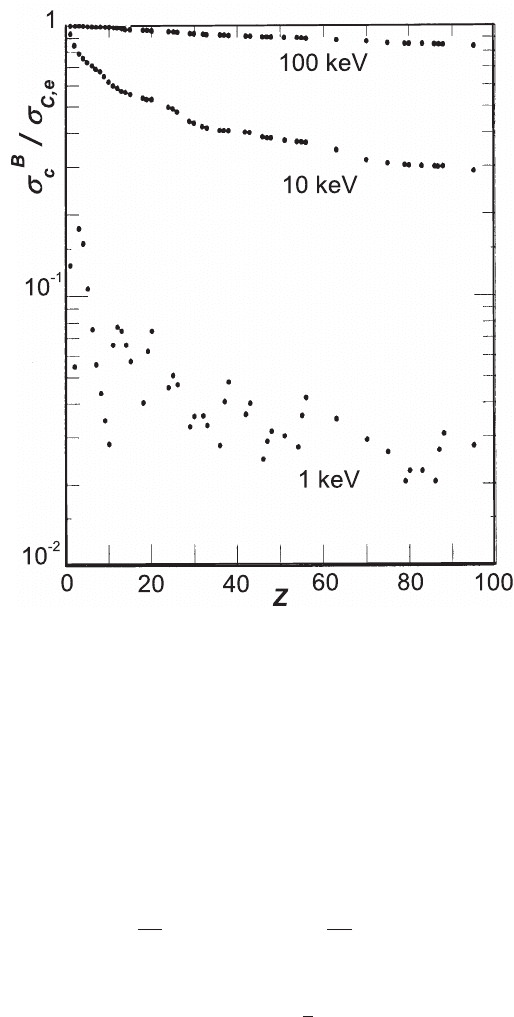
Fig. 2.58 Ratio (calculated by Storm and Israel (1967), see also [Hubbell (1969)]) of the bound

electron Compton cross section σ

to Klein–Nishina theory (see page 159) for incoming photon

energies of 1, 10 and 100 keV as a function of the atomic number Z.

the total Compton cross section is only slightly aﬀected because these variations

almost compensate themselves. The Klein–Nishina diﬀerential cross section on free

electron, assumed at rest, was generalized to the case of electrons in motion [Jauch

and Rohrlich (1955)]: the solid lines in Fig. 2.57 were obtained by averaging on

the appropriate distribution of electron velocities. To take into account the elec-

tron binding eﬀects, the Klein–Nishina equation [i.e., Eq. (2.179)] is modiﬁed by

introducing the so-called incoherent scattering function S(q, Z):

dσ

dΩ

incoh

C,e

= S(q, Z)

dσ

dΩ

C,e

, (2.190)

where q is the momentum transfer in units of mc

, with

q ≈ 2 E sin

at low momentum transfer, i.e., when binding eﬀects play an important role. The

incoherent scattering function gives the probability that an atom be excited or

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 159

ionized as a result of transferring a recoil momentum q to an atomic electron. For

instance, for K-shell electrons only, the observed ratio shown in Fig. 2.57 corresponds

to the incoherent scattering function S(q, Z). The total Compton incoherent cross

section per electron taking into account the binding energy eﬀects can be computed

from Eq. (2.190):

dσ

dΩ

incoh

C,e

dΩ. (2.191)

Figure 2.58 shows the ratios of σ

/σ

C,e

calculated by Storm and Israel (1967) (see

also [Hubbell (1969)]), as a function of the atomic number Z for photon energies

of 1, 10, 100 keV. The incoherent cross section σ

is almost represented by the

Klein–Nishina Compton cross section on free electron above ≈ 100 keV, while it

decreases for lower photon energies and becomes dependent on the atomic number

Z. When the atom takes part as a whole to the interaction process, there is a phase

relation between scattering amplitudes for diﬀerent atomic electrons. The overall

scattering amplitude is a coherent sum of individual contributions. The Rayleigh

scattering is a coherent process by which photons interact with atomic bound elec-

trons, leaving the target atom neither excited nor ionized. This type of interaction

occurs at low photon energies and in high-Z materials, i.e., when the Compton

process is aﬀected by the binding energies of atomic electrons. Detailed calculations

on Rayleigh scattering were carried out (see Section 2.4.4 in [Hubbell (1969)] and

references therein). In these calculations, the charge distribution of all Z electrons

at once was taken into account by means of an atomic form factor F (q, Z) based

on atomic models. The form factor square value gives the probability that the recoil

momentum q is taken up by the whole Z electrons without absorbing energy. The

Rayleigh diﬀerential cross section is given in terms of the atomic form factor by:

dσ

dΩ

= F

(q, Z)

1 + cos

[cm

−1

/atom], (2.192)

where r

1 + cos

/2 is the Thomson diﬀerential cross section, i.e., the limit for

E → 0 of the Klein–Nishina diﬀerential cross section on free electron. The Rayleigh

cross section σ

is computed by integrating Eq. (2.192):

(q, Z)

1 + cos

dΩ [cm

/atom]. (2.193)

References for the calculations of S(q, θ) and F (q, θ) are given in [Hubbell (1969);

Berger, Hubbell, Seltzer, Chang, Coursey, Sukumar and Zucker (2005)]. At high

energy, the Rayleigh scattering is conﬁned to small angles. For instance more than

50% of scattered photons are within 5

◦

at 1 MeV. At low energy, in particular for

high-Z materials, the angular distribution is more enlarged. But in this latter case,

the dominant mode of photon interaction is via the photoelectric eﬀect. A practical