Leroy C., Rancoita P.-G. Principles Of Radiation Interaction In Matter And Detection

Подождите немного. Документ загружается.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

120 Principles of Radiation Interaction in Matter and Detection

ﬁnally, since the solid angle dΩ can be written as dΩ ≈ 2πθdθ for small scattering

angles, we obtain:

Nρ

2Zze

dΩ

dx. (2.124)

Therefore, the probability of collision can be expressed by

= Ξ(θ) dΩ dχ,

where dχ = ρ dx is the thickness of traversed material in units of g cm

−2

; Ξ(θ)

shall be referred to as the diﬀerential scattering probability. From Eq. (2.124) and

introducing the classical electron radius r

= e

/mc

, the scattering probability is

given by

Ξ(θ) dΩ =

2Zze

dΩ

= 4N

zmc

βp

dΩ

−1

]. (2.125)

Equation (2.125) is known as the Rutherford scattering formula (see Sect. 1.5). The

theoretical expression of Ξ(θ) depends on the spin of the incident particle for large

deﬂections. For small deﬂections, the spin dependence can be neglected and, to a

ﬁrst approximation, one can use Eq. (2.125) (see [Rossi and Greisen (1941); Rossi

(1964)] and references therein). A similar calculation can be done for scattering on

atomic electrons. Their contribution is relatively small, being Z times lower.

The ﬁnite size of the nucleus and the nuclear ﬁeld screening by the atomic

electrons reduce the validity of Eq. (2.125). By assuming that the electric charge is

uniformly distributed over a nuclear sphere with radius

' 0.5 r

1/3

(see [Rossi (1964)]), it can be shown [Rossi and Greisen (1941); Rossi (1964)] that

the calculated value of Ξ(θ) is not aﬀected for

θ <

2πr

where λ = h/p is the de Broglie wavelength of the incoming particle, while Ξ(θ)

goes rapidly to 0 at larger values of θ. Thus, we can take into account the ﬁnite size

of the nucleus considering as maximum deﬂected angle:

max

2πr

' 2

p r

1/3

= 2

p α

−1/3

. (2.126)

Furthermore, taking as atomic radius

1/3

(the Thomas–Fermi radius), it can be proven that the nuclear ﬁeld screening by the

outer electrons does not aﬀect the scattering probability for

θ >

2πa

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 121

while Ξ(θ) vanishes for lower θ values (see [Rossi (1964)] and references therein). So

that, the minimum deﬂected angle becomes:

min

2πa

p a

−1/3

mc α

1/3

. (2.127)

When a charged particle traverses a thickness dχ of material, successive small

angular deﬂections can be considered as statistically independent. The mean square

of the scattering angle



at a depth χ + dχ is given by its value at χ in addition

to the mean square of the scattering angle in the thickness dχ:



= dχ

2π

max

min

Ξ(θ) dΩ;

thus, by means of Eq. (2.125), we get



= dχ

2π

max

min

zmc

βp

dΩ

Since for small scattered angles dΩ ≈ θ dφ dθ (where φ is the azimuthal angle), one

has



= 4N

zmc

βp

dχ

max

min

2πθ dθ

and, using Eqs. (2.126, 2.127),



= 8πN

zmc

βp

max

min

dχ

= 8πN

zmc

βp

pα

−1/3

mcα

1/3

dχ.

Furthermore, with the approximation A ≈ 2Z, we obtain



= 8πN

zmc

βp

1/3

dχ

' 16πN

ρr

zmc

βp

173

1/3

dx,

and, ﬁnally, since numerically

Nρ

αZ

173

1/3

≈

where X

is the radiation length for the case of complete screening in the Born

approximation [see Eqs. (2.106, 2.114)], we have:



' 4

zmc

βp

dx. (2.128)

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

122 Principles of Radiation Interaction in Matter and Detection

By traversing a thickness L in cm of material (see Fig. 2.40) and assuming that

the energy loss can be neglected, we obtain the so-called Rossi–Greisen equation for

the mean square of the scattering angle:



zmc

βp

= 4

zmc

βp

= E

, (2.129)

where

4π(mc

)

i.e., E

= 21.2 MeV. Furthermore, the rms (i.e., the root mean square) value of the

scattering angle is:

rms

hθ

i = E

Instead of considering the total deﬂection θ, it is often convenient to consider its

projection θ

proj

onto a plane containing the direction of the initial particle trajec-

tory. It can be shown that, under the assumption of small deﬂections, we have (see,

for instance, [Fernow (1986)]):



proj



and

rms

proj

√

rms

The multiple scattering eﬀect is expressed in the Rossi–Greisen equation

[Eq. (2.129)] in terms of the radiation length of the material. However, it has to

be noted that the radiation length is only used as a numerical approximative fac-

tor in Eqs. (2.128, 2.129), since the multiple Coulomb scattering is not a radiative

phenomenon.

More detailed calculations were performed [Moli`ere (1947); Bethe (1953)]. In par-

ticular in [Moli`ere (1947)], Moli`ere has taken into account the screening eﬀect. The

multiple scattering results are roughly Gaussian only for small deﬂection angles,

but with non-Gaussian tails at larger angles. Although Eq. (2.129) can provide an

approximate calculation, Highland, Lynch and Dahl [Highland (1975)] proposed a

few modiﬁcations to the Rossi–Greisen equation in order to reproduce Moli`ere’s

theory in a more accurate way. For instance, for the 98% of the projected central

distribution and to better than 11%, they obtain:

rms

proj

13.6 MeV

βcp

1 + 0.038 ln

¶¸

. (2.130)

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 123

Table 2.9 The values of the j and f parameters

for calculating the multiple scattering eﬀect on

electrons and positrons in Al and Pb absorbers

from [Rohrlich and Carlson (1954)].

j f

0.297 0.014

−

0.305 0.034

0.311 0.057

−

0.430 0.052

After undergoing multiple Coulomb scattering, particles emerging from a mate-

rial of thickness L are displaced from their original trajectory (see Fig. 2.40). Let us

call X and Y the two coordinate axes in a reference frame on the plane perpendic-

ular to the initial trajectory of the particle and centered on the impinging particle

position. The emerging-particle lateral shift was evaluated by Rossi (see [Rossi and

Greisen (1941); Rossi (1964)]). For the case in which the energy-loss process can be

neglected, the mean square lateral displacement along an axis (for instance the Y

axis) is approximately given by



. (2.131)

The cross section (neglecting radiative corrections) for the elastic scattering

of electrons and positrons by the Coulomb ﬁeld of a charge Ze was derived by

Mott (1929) and calculated for light and heavy nuclei. Electrons and positrons

show sizeable diﬀerences with respect to the multiple scattering eﬀect, particularly

when they undergo scattering at large angles. For heavy elements, the electron–

positron diﬀerences are large and can amount up to a factor three. The electron

cross section always exceeds the positron cross section. Furthermore, Rohrlich and

Carlson (1954) estimated the multiple scattering eﬀect on electrons and positrons

taking into account the collision energy-loss. The cosine of the multiple scattering

angle averaged over all electrons (or positrons), whose initial kinetic energy E

has dropped down to E = γmc

, is given by

hcos θi =

G(γ

)

G(γ)

where

G(γ) =

γ + 1

γ − 1

exp

The values of the j and f parameters for electrons and positrons are given in

Table 2.9 for Al and Pb absorbers [Rohrlich and Carlson (1954)].

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

124 Principles of Radiation Interaction in Matter and Detection

Fig. 2.41 Huyghens construction of the spherical wavefronts at successive times. r is the refraction

index of the material and β is the particle velocity in units of the speed of light.

2.2.2 Emission of

Cerenkov Radiation

The emission of electromagnetic radiation, a remarkable phenomenon discovered by

Cerenkov (1937) and explained theoretically by Frank and Tamm (1937), occurs in

a medium at the passage of a charged particle with a velocity v larger than the

phase velocity of light in that medium, i.e., when

v > c

≡

where r is the index of refraction. This emitted radiation is referred to as

Cerenkov

radiation.

The classical theory explains this eﬀect by an asymmetric polarization of the

medium in front and at the rear of the charged particle, giving rise to a net and

time varying electric-dipole momentum. To visualize the eﬀect, let us consider a

charged particle traversing a medium. The atoms of the dielectric can be assumed

to be approximately spherical in regions far away the particle path, while becoming

elongated by interaction with the particle electromagnetic-ﬁeld, so that the centers

of gravity of the positive and negative charge inside atoms do not coincide any-

more. Thus, for suﬃciently fast

‡

particles, a polarized region is generated following

an axial symmetry. In this region, individual atoms act as electric dipoles and create

a net overall dipole ﬁeld. It is this dipole ﬁeld which is responsible for the emission

of the electromagnetic pulses of the

Cerenkov radiation.

In general, there is a constructive interference between wavelets propagated from

successive areas along the particle path, when the particle velocity is larger than

the phase velocity of light in that medium. From an Huygens-type construction in

wave optics (see Fig. 2.41), a coherent wavefront is generated and moves with a

velocity c

at angle θ, whose cosine is

cos θ =

βc

βr

. (2.132)

‡

In this case, the particle speed is considered with respect to the phase velocity of light in the

medium.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 125

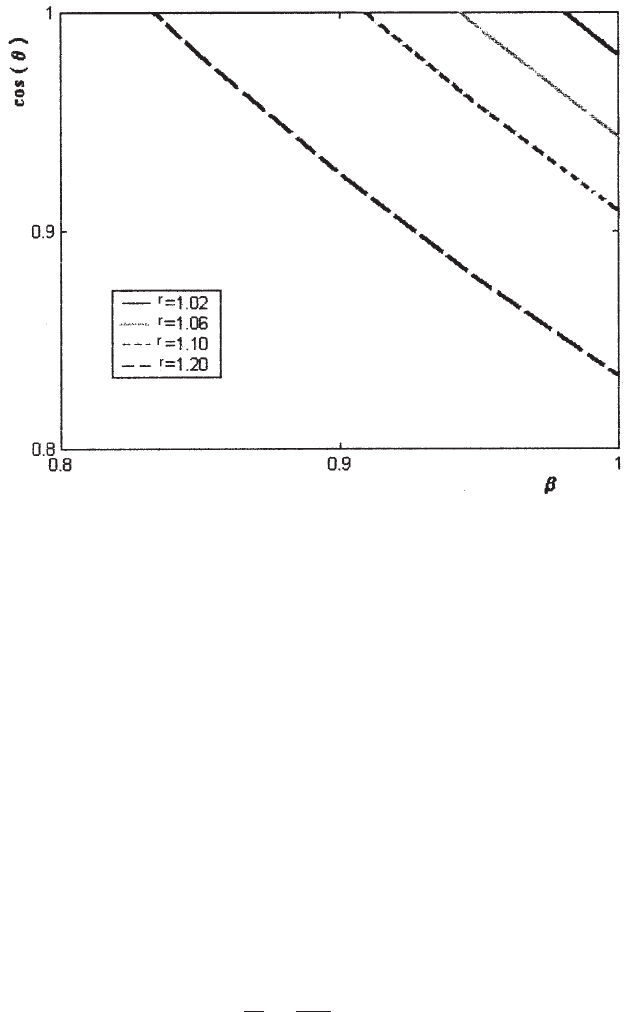
Fig. 2.42 Cosine of the

Cerenkov angle θ versus the particle velocity β in units of the speed of

light, for various values of the refractive index r.

In Fig. 2.42, the cosine of the

Cerenkov angle θ is shown as a function of the

particle velocity for various values of the index of refraction. It has to be noted that

the particle mass does not play any role upon the emission angle. Furthermore,

the emission angle increases with the particle velocity contrary to the radiation

emitted in a bremsstrahlung process [see Eq. (2.113)]. In addition, the emission

angle depends on the wavelength λ of the

Cerenkov radiation, because the index of

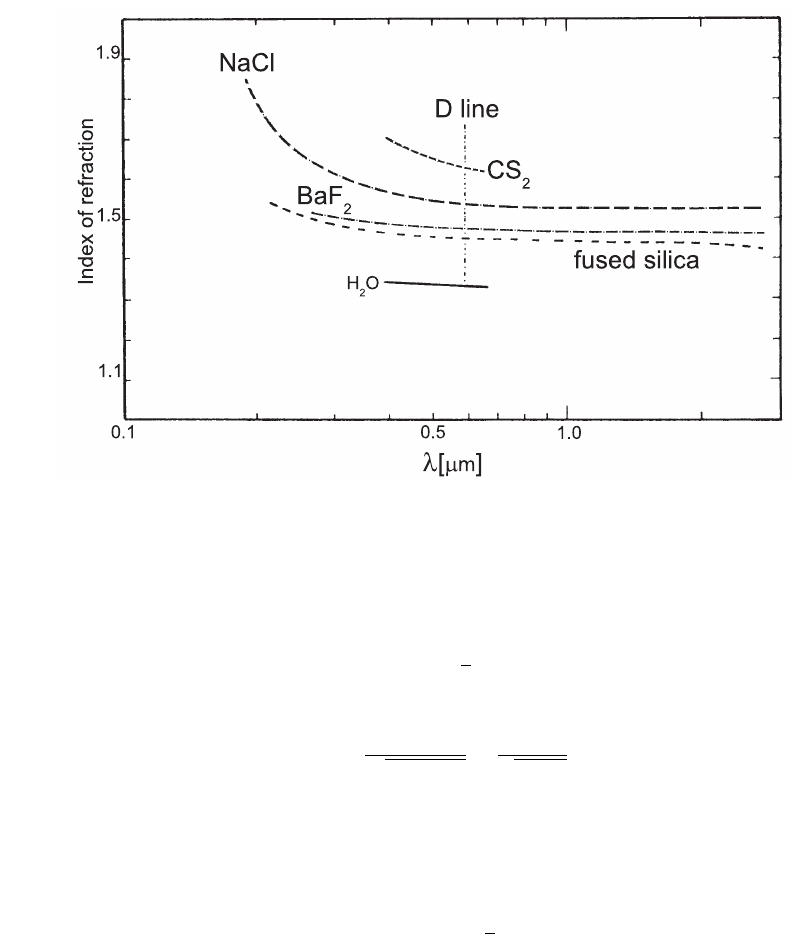
refraction depends on λ (see for instance Fig. 2.43 and [Physics Handbook (1972)]):

the variation d r(λ)/d λ is referred to as dispersion and is largest in the ultraviolet

region. Its variation with temperature is generally small. Indices of refraction of

liquid and solid media are shown in Fig. 2.43, in Table 2.10 and on the web for

0.041 < λ < 41 nm (e.g., see [Henke, Gullikson and Davis (1993)]). Typical

Cerenkov

radiations correspond to frequencies between the blue region of the visible and near-

visible part of the electromagnetic spectrum. Note that the energy (E

) of a photon

with a wavelength λ (in vacuum) is given by:

≈

1.24

× 10

[eV], (2.133)

where λ is in units of nm.

The

Cerenkov radiation starts to be emitted at a threshold particle velocity

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

126 Principles of Radiation Interaction in Matter and Detection

Fig. 2.43 Index of refraction of various materials as a function of the wavelength in units of

µm (modiﬁed with the permission of Cambridge University Press from [Fernow (1986)], see

also [Physics Handbook (1972)]). The vertical dashed line refers to the D line wavelength of Na,

which is often used to quote refractive indices.

thres

c and θ = 0

◦

[see Eq. (2.132)] when

thres

, (2.134)

or, rewriting Eq. (2.134) in an equivalent way,

thres

1 − β

thres

√

− 1

. (2.135)

Using Eq. (2.135), we can estimate that for an index of refraction of ≈ 1.58 (i.e., for

a plastic scintillator) γ

thres

is ≈ 1.29, while is ≈ 34.1 for r ≈ 1 + 4.3 ×10

−4

(i.e., for

the CO

gas at ST P ). Conversely, the maximum angle of emission occurs when the

particle speed approaches the speed of light:

max

= arccos

. (2.136)

In practice [see Eq. (2.132)], the condition βr > 1 is usually satisﬁed from the

ultraviolet to near infrared portion of the electromagnetic spectrum, i.e., for photon

wavelengths (in vacuum) between ≈ (0.2–1.2) µm, but does not extend to the X-ray

region where r is typically < 1.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 127

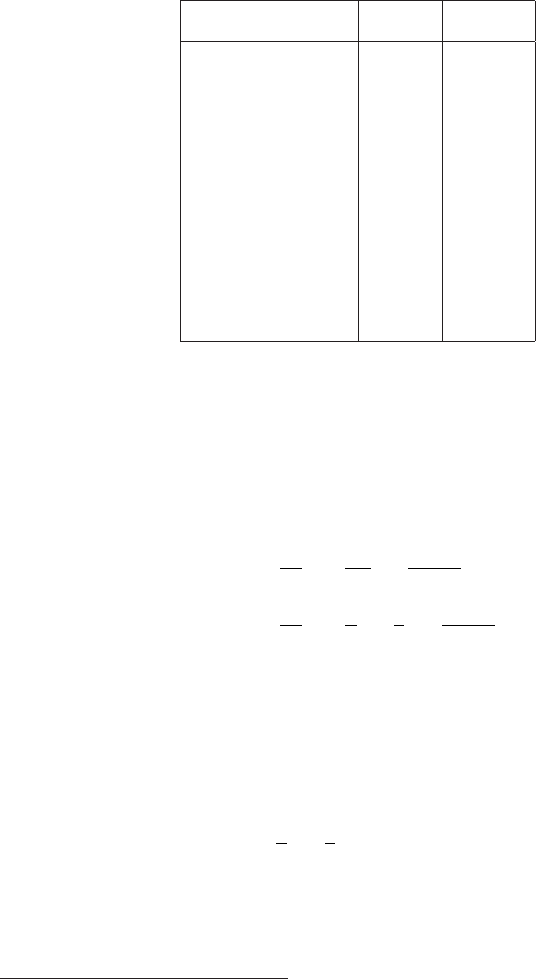
Table 2.10 Index of refraction of liquid and solid

radiators for sodium light at (20−25)

◦

C (see [Fer-

now (1986)] and references therein).

Material r ρ

g/cm

Water 1.333 1.00

Carbon tetrachloride 1.459 1.591

Glycerol 1.474 1.26

Toluene 1.494 0.867

Styrene 1.545 0.91

Lucite 1.49 1.16–1.20

Plastic scintillator 1.58 1.03

Crystal quartz 1.54 2.65

Borosilicate glass 1.474 2.23

Lithium ﬂuoride 1.392 2.635

Barium ﬂuoride 1.474 4.89

Sodium iodide 1.775 3.667

Cesium iodide 1.788 4.51

Sodium chloride 1.544 2.165

Silica aerogel 1+0.25ρ 0.1–0.3

In a quantum-mechanical treatment of the process [Ginzburg (1940); Marmier

and Sheldon (1969)], the classical result is modiﬁed to take into account the reaction

of the emitted radiation onto the charged-particle motion (see Fig. 2.44), when the

incoming velocity is βc. Owing to momentum and energy conservation, the cosine

of the

Cerenkov angle is (see Chapter 4.9 in [Marmier and Sheldon (1969)]):

cos θ

βr

¶µ

− 1

2 r

βr

¶µ

− 1

2 r

, (2.137)

where λ

and p are the de Broglie wavelength and the momentum of the inco-

ming particle, respectively, and (h/λ) is the momentum of the

Cerenkov photon. In

Eq. (2.137), a second term is present with respect to Eq. (2.132): this term expresses

a small reaction correction. For instance, for a 10 GeV/c particle and for an emitted

photon with a wavelength

†

(in vacuum) of 400 nm, we have

¶µ

≈ 3 × 10

−10

(becoming ≈ 3 ×10

−9

at 1 GeV); thus, this term makes the overall reaction correc-

tion negligible.

The intensity

∗

of the

Cerenkov radiation for a particle of charge ze traversing a

†

This wavelength corresponds to a photon momentum of ≈ 3 eV/c.

∗

The intensity is the number of photons emitted per unit length of particle path and per unit of

frequency.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

128 Principles of Radiation Interaction in Matter and Detection

thickness dx of an absorber is given by:

dx dν

4π

1 −

2πz

1 −

. (2.138)

Or equivalently, the intensity per unit of wavelength (in vacuum, for which λν = c)

dx dλ

2πz

1 −

This equation shows that the number of quanta per wavelength interval is pro-

portional to 1/λ

and that the short wavelengths of the spectrum dominate. From

Eq. (2.138), the energy loss by

Cerenkov radiation becomes

−

βr>1

dx dν

hν dν

and, for α = e

/(~c), it can be expressed by:

−

4π

βr>1

1 −

ν dν , (2.139)

where the integration is extended over all frequencies for which βr > 1 and ν is the

emitted-photon frequency.

To a ﬁrst approximation, we can assume that the index of refraction is roughly

constant (see Fig. 2.43) in the region of wavelengths (in vacuum) from ≈ 350 up to

≈ 500 nm, i.e., the region which covers most of the

Cerenkov radiation spectrum and

overlaps with the highest quantum eﬃciency region of typical commercial photo-

multipliers. Equations (2.138, 2.139) can be integrated in this range of wavelengths

to obtain both the number of emitted-photons and the particle energy-loss per unit

of length. Using Eq. (2.132), we estimate the number of emitted photons per unit

of length by means of Eq. (2.138):

4π

1 −

dν

2πz

sin

θ dν

2πz

sin

θ (ν

− ν

)

= 2πz

−

sin

≈ 393 z

sin

θ [quanta/cm], (2.140)

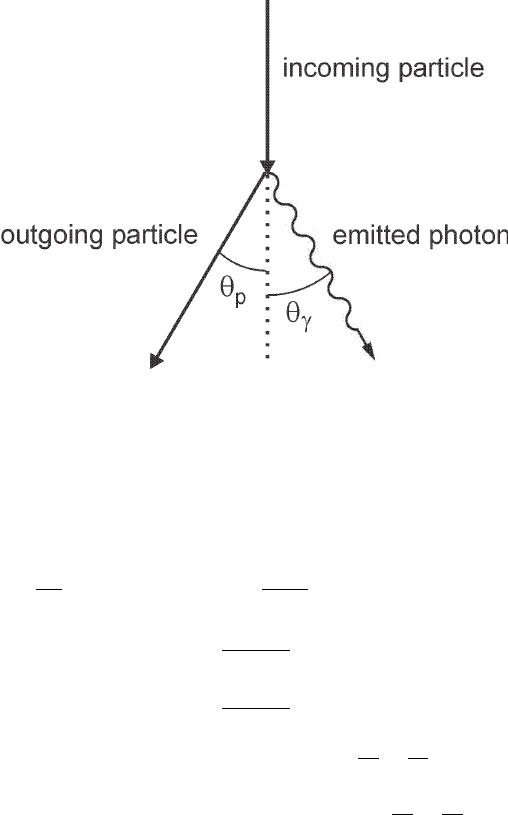
January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Electromagnetic Interaction of Radiation in Matter 129

Fig. 2.44 Emission of a photon with energy hν at an angle θ

from a particle scattered at an

angle θ

where λ

and λ

are 350 and 500 nm, respectively. The energy loss per unit of length

can be determined using Eq. (2.139):

−

C,(350−700)nm

dx dν

hν dν

4π

sin

θν dν

2π

sin

− ν

= 2π

sin

−

= 2π

sin

−

≈ 1.18 × 10

−3

× z

sin

θ [MeV/cm]. (2.141)

Even considering larger intervals of integration, the energy loss by

Cerenkov ra-

diation is quite small (usually much less than 1%, see Table 2.3) in comparison

with the energy loss by collision in solids. In gases with Z > 7, the energy loss by

Cerenkov radiation can amount to less than 1% of the collision loss of minimum

ionizing particles, while for hydrogen and helium it can amount to ≈ 5% (see for

instance [Grupen (1996)] and references therein). The energy loss by

Cerenkov ra-

diation can be detected because many low energy quanta are emitted in the small

solid angle determined by the

Cerenkov angle.