Леонов Г.А., Шумафов М.М. Проблемы стабилизации линейных управляемых систем

Подождите немного. Документ загружается.

241

Тогда имеем

= (

)

= 8ε

(1 + δ

Ω

= (

−

)

= 8ε

(1 − δ

Ω

−

Ω

1 + δ

1 − δ

−

1 − δ

1 + δ

= 2δ

+ o(δ

Поэтому справедливы разложения (при ε

+ δ

→ 0 ):

cos Ωτ = 1 − 4ε

(1 − δ

) + 8ε

/3 + o(ε

+ δ

sh kτ = 1 + 4ε

(1 + δ

) + 8ε

/3 + o(ε

+ δ

(k/Ω −Ω/k) sin Ωτ · sh kτ = 16ε

+ o(ε

+ δ

Следовательно, условие устойчивости (7) перепишется так:

2(1 − 16ε

+ 8ε

+ 16ε

/3 + o(ε

+ δ

) + 16ε

+ o(ε

+ δ

) < 2.

Пренебрегая бесконечно малыми o(ε

+ δ

) высшего порядка, из по-

следнего неравенства получаем

3δ

< 2ε

или

3g` < 2ac.

Это условие можно переписать так :

√

. (8)

Таким образом, условие устойчивости (7) свелось к неравенству

(8), которое будет выполнено, если период колебаний T точки подве-

са маятника достаточно мал, и, соответственно, частота колебаний

N = 1/T (число колебаний точки подвеса в единицу времени) доста-

точно большая.

Итак, при достаточно быстрых колебаниях точки подвеса маят-

ника (при достаточно большой частоте N ) отображение H устойчиво

(по Ляпунову) и, следовательно, в силу теоремы 2 из § 2, гл.IV поло-

жение равновесия (x

= 0, x

= 0) — верхнее положение равновесия

маятника — устойчиво (по Ляпунову).

2. Стабилизация с помощью непрерывных периодических

функций ([259,260]). Рассмотрим теперь возможность стабилизации

242

верхнего положения равновесия маятника с помощью функций s(t)

вида (3).

Система уравнений (4) движения маятника с функцией s(t) ви-

да (3) не имеет пока стандартного вида (23) из § 2. Чтобы привести

систему (4),(3) к виду (23) из § 2, сделаем в ней линейное преобразо-

вание координат (с переменными коэффициентами)

= y

= −(β sin ωt)y

+ y

(9)

Уравнения движения маятника в новых координатах y

, y

принима-

ют вид

˙y

= (β sin ωt)y

+ y

˙y

= [ν

− s

+ αβ sin ωt − β

sin

ωt]y

+ [−α + β sin ωt]y

(10)

Заметим, что преобразование (9) сохраняет свойство устойчивости

(экспоненциальной), так как матрица

Φ(t) =

1 0

−β sin ωt 1

коэффициентов при y

и y

ограничена и det Φ(t) ≡ 1 на промежутке

[0, +∞).

Система (10) уже имеет стандартный вид (23) из § 2 и, поэтому, мы

можем воспользоваться доказанной в § 2 теоремой 3, согласно кото-

рой система (10) (а значит, и система (4)) экспоненциально устойчива

равномерно относительно ω для всех ω ≥ ω

, где ω

— достаточно

большое число, если соответствующая усредненная система асимп-

тотически устойчива, т.е. когда гурвицева следующая матрица

2π

A(τ) dτ,

где

A(τ) =

β sin τ 1

− s

+ αβ sin τ − β

sin

τ −α + β sin τ

Элементарные вычисления дают:

0 1

− s

− β

/2 −α

243

Характеристический многочлен матрицы A

имеет вид

+ αp + s

+ β

/2 − ν

Отсюда видно, что матрица A

гурвицева тогда и только тогда, когда

< s

+ β

/2 (11)

(поскольку α > 0).

Таким образом, условие (11) есть достаточное условие экспонен-

циальной устойчивости системы (4),(3).

Итак, верхнее положение равновесия маятника становится устой-

чивым, если выполнено неравенство (11).

Замечание. Как легко видеть, условие стационарной стабили-

зации (s(t) ≡ s

= const) верхнего положения равновесия маятника

имеет вид

< s

Отсюда и из (11) хорошо видно, насколько введение переменного

слагаемого βω cos ωt в выражении функции s(t) (см. (3)) расширяет

границу области устойчивости.

§ 4. Высокочастотная стабилизация линейных систем

Пусть дана система

˙x = Ax + bu, y = c

∗

x (x ∈ R

), (1)

со скалярным входом u ∈ R и скалярным выходом y ∈ R, где A —

вещественная постоянная (n × n)-матрица, а b, c — одностолбцовые

n-мерные векторы (b, c ∈ R

Наша задача — найти обратную связь

u(t) = s(t)y (2)

такую, чтобы тривиальное решение x(t) ≡ 0 (и, следовательно, в

силу предложения 2 из § 2 любое решение x(t)) замкнутой системы

(1), (2), т.е. системы

˙x = (A + s(t)bc

∗

)x, (x ∈ R

), (3)

было экспоненциально устойчивым.

Рассмотрим класс M функций s(t) таких, что

s(t) = s

(t) + s

(t), (4)

244

где s

(t) и s

(t) непрерывные и периодические функции, причем

функция s

(t) имеет нулевое среднее на периоде, т.е.

(τ) dτ = 0 (5)

(T > 0 — период функции s

(t)).

Стабилизирующую функцию s(t) в (2) будем искать в классе M.

1. Приведение замкнутой системы к специальной форме.

Докажем следующую лемму.

Лемма 1. Существует такое преобразование векторной пере-

менной x

x = Φ(t)z (z ∈ R

), (6)

где

Φ(t) = e

`(t)bc

∗

(7)

`(t) (t ≥ 0) — непрерывно дифференцируемая функция, удовлетво-

ряющая условию

`(t) = s

(t), (8)

что при таком преобразовании система (3) приводится к виду

˙z = [Φ(t)

−1

AΦ(t) + s

(t)bc

∗

]z. (9)

При этом система (3) экспоненциально устойчива тогда и только

тогда, когда экспоненциально устойчива система (9).

Д о к а з а т е л ь с т в о . Сделаем преобразование (6) в системе

(3). Имеем

Φ(t)z(t) + Φ(t) ˙z(t) = ˙x(t) = (A + s(t)bc

∗

)Φ(t)z(t).

Отсюда, с учетом (4) получаем уравнение для новой векторной

функции z(t):

˙z(t) = Φ(t)

−1

[(A + s

(t)bc

∗

+ s

(t)bc

∗

)Φ(t) −

Φ(t)]z(t). (10)

Из равенства

`(t)(bc

∗

)

∞

k=0

(`(t))

(bc

∗

)

245

следует, что матрица bc

∗

коммутирует с Φ(t), и , поэтому, из (7), (8)

получаем

Φ(t) = s

(t)bc

∗

Φ(t).

Заметим, что поскольку s

(t) — периодическая функция, удовлетво-

ряющая условию (5), то из (8) следует, что `(t) будет тоже периоди-

ческой функцией с тем же периодом T .

Следовательно, уравнение (10) принимает вид (9):

˙z = Φ(t)

−1

(A + s

(t)bc

∗

)Φ(t)z =

= [Φ(t)

−1

AΦ(t) + s

(t)bc

∗

Вторая часть утверждения леммы следует из следующих свойств

матричной функции Φ(t):

1) Φ(t) ограничена на промежутке [0, +∞), т.е. sup

kΦ(t)k < ∞ при

t ∈ [0, +∞);

2) 0 < m ≤ |det Φ(t)| ≤ M при t ∈ [0. + ∞), где m и M —

некоторые положительные константы.

(Свойства 1) и 2) вытекают из вида (7) функции Φ(t), периодич-

ности функции `(t) и равенства (см. следствие леммы 2 из § 4, гл.I)

det e

`(t)bc

∗

= e

`(t)c

∗

)

Легко видеть, что обратная матрица Φ(t)

−1

тоже обладает свой-

ствами 1) и 2).

Поэтому как преобразование (6), так и обратное к нему преобра-

зование z = Φ(t)

−1

x не меняют свойства экспоненциальной устойчи-

вости. Лемма 1 доказана.

Далее будем различать два случая:

1) c

∗

b 6= 0 и 2) c

∗

b = c

∗

Ab = 0.

2. Стабилизация в случае c

∗

b 6= 0. Имеет место следующая

Теорема 1 ([259]). Пусть в системе (1) c

∗

b 6= 0. Предположим,

что существуют вещественные числа α и κ ≥ 0 такие, что мат-

рица

A + κ(c

∗

b)bc

∗

A + (α − κc

∗

Ab)bc

∗

(11)

гурвицева. Тогда существует такая периодическая функция

s(t) = α + βω cos ωt, (12)

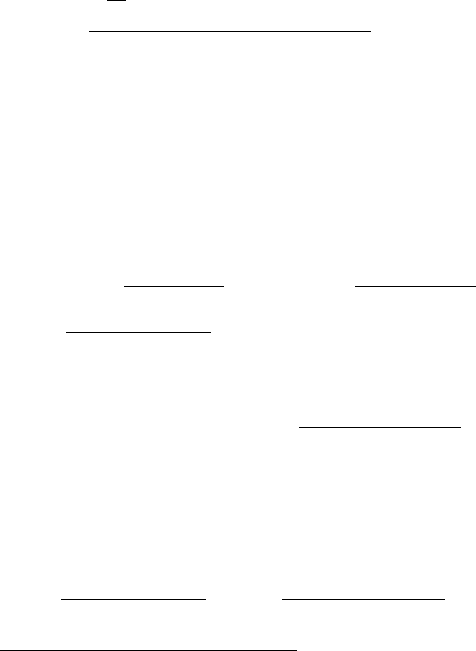
246

где ω достаточно большое число, а β ∈ R такое, что

2π

exp(βc

∗

b sin t)dt

− 1

∗

= κ, (13)

что замкнутая система (3) равномерно экспоненциально устойчи-

ва при достаточно больших ω.

Д о к а з а т е л ь с т в о . Так как c

∗

b 6= 0, то используя очевидное

соотношение

(bc

∗

)

= (c

∗

k−1

∗

преобразуем матрицу Φ(t) (см.(7)) к виду:

Φ(t) = I +

∞

k=1

`(t)

(bc

∗

)

= I +

∞

k=1

`(t)

∗

k−1

∗

= I +

exp[c

∗

b`(t)] − 1

∗

(14)

Аналогично,заменяя в (14) `(t) на −`(t), получим

Φ(t)

−1

= exp[−`(t)bc

∗

] = I +

exp[−c

∗

b`(t)] − 1

∗

. (15)

Учитывая (14) и (15), и, используя очевидное равенство

(bc

∗

A)bc

∗

= (c

∗

Ab)bc

∗

приведем систему (7) к виду:

˙z =

A +

exp[c

∗

b`(t)] − 1

∗

Abc

∗

exp[−c

∗

b`(t)] − 1

∗

A+

2 − exp[c

∗

b`(t)] − exp[−c

∗

b`(t)]

∗

Ab)bc

∗

+ s

(t)bc

∗

] z

. (16)

Стабилизирующую функцию s(t) возьмем в виде (4), где

(t) = α, (17)

(t) = βω cos ωt, (18)

α, β и ω — вещественные параметры. Тогда согласно (8) имеем

`(t) = β sin ωt + `

, (19)

где `

постоянная интегрирования, которая будет выбрана ниже.

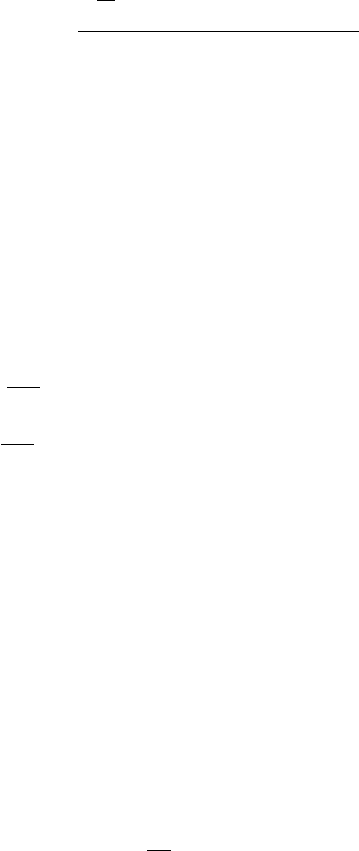
247

Введем функцию µ : R → R, определяемую следующим образом:

µ(β) =

2π

exp[βc

∗

b sin t] dt

− 1

∗

Легко видеть, что функция µ 1) четная: µ(−β) = µ(β) и 2) имеет

областью значений промежуток [0, +∞).

Действительно, свойство 1) следует из очевидного равенства

2π

exp[−βc

∗

b sin t]dt =

2π

exp[βc

∗

b sin t]dt,

а свойство 2) — из 1), равенств µ(0) = 0, µ

(0) = 0, и того, что вторая

производная

(β) =

2π

(sin t) exp[βc

∗

b sin t]dt

2π

exp[βc

∗

b sin t]dt ·

2π

(sin t)

exp[βc

∗

b sin t]dt

строго положительна.

Таким образом, уравнение µ(β) = µ

, µ

∈ [0, +∞), всегда имеет

решение относительно β.

Заметим, что система (16), (17), (19) с достаточно большим пара-

метром ω является системой с быстрым временем и имеет стандарт-

ный вид (см. (23) из § 2):

˙z = B(ωt)z,

где через B(τ), τ = ωt обозначена матрица системы (16), (17), (19)

(выражение, стоящее в квадратной скобке в (16) с учетом (17), (19)).

Поэтому к ней можно применить теорему 3 из § 2. Найдем матрицу

2π

B(τ ) dτ.

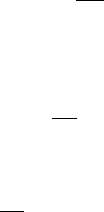
248

Выберем константу `

в (19) так:

∗





ln 2π − ln

2π

exp[βc

∗

b sin t]dt





Тогда

2π

exp[c

∗

b(β sin t + `

)]dt − 1 = 0,

2π

exp[−c

∗

b(β sin t + `

)]dt − 1 = (c

∗

µ(β).

С учетом последних соотношений получаем, что

= A + (c

∗

b)µ(β)bc

∗

A + (−c

∗

Abµ(β) + α)bc

∗

Выберем теперь число β таким, чтобы

µ(β) = κ, (20)

где κ ≥ 0 — число, фигурирующее в теореме 1. Тогда матрица B

совпадает с (11) и по условию теоремы 1 будет гурвицевой.

Следовательно, в силу теоремы 3 из § 2 система (16),(17),(19) бу-

дет равномерно (относительно ω) экспоненциально устойчивой при

достаточно больших значениях ω. По доказанной выше лемме 1 по-

следнее утверждение верно и для системы (3).

Соотношения (12) и (13) следуют из (4), (17), (18) и (20) соответ-

ственно. Теорема 1 доказана.

3. Стабилизация в случае c

∗

b = c

∗

Ab = 0. Определим и здесь

матрицу Φ(t) по формуле (7) с функцией `(t) ∈ C

[0, +∞), удовле-

творяющей условию (8).

Так как c

∗

b = 0, то матрицы Φ(t) и Φ(t)

−1

(см. (14) и (15)) прини-

мают вид:

Φ(t) = I + `(t)bc

∗

, (21)

Φ(t)

−1

= I − `(t)bc

∗

. (22)

С учетом (21), (22) и равенства c

∗

Ab = 0, система (9) принимает вид:

˙z = [A + `(t)[A, bc

∗

] + s

(t)bc

∗

]z, (23)

249

где

[A, bc

∗

] = A(bc

∗

) − (bc

∗

(коммутатор матриц A и bc

∗

Заметим, что система (23) имеет такой же вид, что и система (3).

Будем искать функцию `(t), как и s(t), в классе M, т.е. положим

`(t) = `

(t) + `

(t), (24)

где `

(t) и `

(t) — непрерывные периодические функции, причем `

(t)

имеет нулевое среднее на периоде.

Следующая лемма аналогична лемме 1.

Лемма 2. Пусть c

∗

b = c

∗

Ab = 0. Тогда существует такое пре-

образование векторной переменной z

z = Ψ(t)ξ (ξ ∈ R

) (25)

где

Ψ(t) = e

m(t)[A,bc

∗

]

, (26)

m(t) (t ≥ 0) — непрерывно дифференцируемая функция, удовлетво-

ряющая условию

˙m(t) = `

(t), (27)

что при таком преобразовании система (23) приводится к виду:

ξ =

Ψ(t)

−1

AΨ(t) + `

(t)[A, bc

∗

] + s

(t)bc

∗

ξ. (28)

При этом преобразование (25) сохраняет свойство экспоненци-

альной устойчивости.

Д о к а з а т е л ь с т в о . Замена переменных (25) приводит

систему (23) к аналогичному (10) виду

ξ = Ψ(t)

−1

[(A + `

(t)[A, bc

∗

] + `

(t)[A, bc

∗

] +

(t)bc

∗

)Ψ(t) −

Ψ(t)

ξ.

(29)

Поскольку

m(t)[A,bc

∗

]

∞

k=0

m(t)

[A, bc

∗

]

то матрица [A, bc

∗

] коммутирует с матрицей Ψ(t), и, следовательно,

из (26), (27) будем иметь

Ψ(t) = `

(t)[A, bc

∗

]Ψ(t).

250

Следовательно, система (29) принимает вид

ξ = Ψ(t)

−1

[A + `

(t)[A, bc

∗

] + s

(t)bc

∗

]Ψ(t) ξ. (30)

Так как c

∗

b = c

∗

Ab = 0, то

[A, bc

∗

](bc

∗

) = (bc

∗

)[A, bc

∗

] = 0,

и, поэтому,

(bc

∗

)Ψ(t) = Ψ(t)

−1

(bc

∗

) = bc

∗

. (31)

Так как матрица [A, bc

∗

] коммутирует с Ψ(t), то из равенств (31)

следует, что систему (30) можно переписать в виде (28).

Вторая часть утверждения леммы 2 доказывается аналогично со-

ответствующей части леммы 1 с использованием того факта, что

функция m(t), удовлетворяющая условию (27), периодическая (так

как `

(t) периодическая и имеет нулевое среднее на периоде). Лемма

2 доказана.

Докажем теперь следующую теорему.

Теорема 2 ([259]). Пусть в системе (1) c

∗

b = c

∗

Ab = 0. Пред-

положим, что существуют вещественные числа α и κ ≥ 0 такие,

что матрица

A − 3κ(c

∗

b)bc

∗

A + (α + κc

∗

b)bc

∗

(32)

гурвицева.

Тогда существует такая периодическая функция

s(t) = α + γω

cos ωt, (33)

где ω — достаточно большое число, а γ ∈ R такое, что

= κ, (34)

что замкнутая система (3) равномерно экспоненциально устойчи-

ва при достаточно больших ω.

Д о к а з а т е л ь с т в о . Поскольку по условию теоремы

∗

b = c

∗

Ab = 0, то легко проверить, что

[A, bc

∗

]

= −(c

∗

b)bc

∗

[A, bc

∗

]

= 0.