Леонов Г.А., Шумафов М.М. Проблемы стабилизации линейных управляемых систем
Подождите немного. Документ загружается.


231
где
α = inf
kxk=1
q(x), β = sup
kxk=1
q(x).
Для любого вектора ex ∈ R
n
, очевидно, ex/kexk — единичный вектор и
поэтому для него имеет место 4. Отсюда следует утверждение лем-
мы.
Замечание. На самом деле, в лемме
α = min
j
λ
j
(Q), β = sup
j
λ
j
(Q),
где λ
j
(Q), (j = 1, ··· , n) — собственные числа матрицы Q. Но для
дальнейшего это нам не понадобится.
Теорема 1. Пусть существует положительно определенная квад-
ратичная форма
V (x) = x
∗
Hx, x ∈ R
n
(H = H
∗
),
производная которой
˙
V (x) в силу системы (1) удовлетворяет нера-
венству
˙
V (x) ≤ −W (x), (5)
где
W (x) = x
∗
Gx, x ∈ R
n
(G = G
∗
)
— положительно определенная квадратичная форма.
Тогда тривиальное решение x(t) ≡ 0 системы (1) экспоненциаль-
но устойчиво при t → +∞.
Д о к а з а т е л ь с т в о. В силу вышедоказанной леммы для квад-
ратичных форм V (x) и W (x) существуют соответственно числа
0 < α
1
< β
1
и 0 < α
2
< β
2
такие, что
α
1
· kxk
2
≤ V (x) ≤ β
1
kxk
2
, (6)
α
2
· kxk
2
≤ W (x) ≤ β
2
kxk
2
. (7)
Из неравенств (5)–(7) имеем
˙
V ≤ −α
2
kxk
2
≤ −
α
2
β
1
V (x),
т.е.
˙
V ≤ −2αV,

232
где α = −α
2
/2β
1
. Интегрируя последнее дифференциальное неравен-
ство, будем иметь
V (t) ≤ V (t
0
)e
−2α(t−t
0
)
∀t ≥ t
0
, (8)
где V (t) ≡ V (x(t)), x(t) — решение уравнения (1) с начальным усло-
вием x(t
0
) = x
0
(x
0
∈ R
n
). Используя оценку (8) и неравенства (6),
имеем
kx(t)k
2
≤
1
α
1
V (x(t)) ≤
β
1
α
1
kx(t
0
k
2
· e
−2α(t−t
0
)
(t ≥ t
0
)
т.е.
kx(t)k ≤ N · kx(t
0
)k · e
−α(t−t
0
)
∀t ≥ t
0
,
где N =
p
β
1
/α
1
. Следовательно, нулевое решение x(t) ≡ 0 экспонен-
циально устойчиво при t → +∞. Теорема доказана.
2. Теорема об экспоненциальной устойчивости линейной
системы с малым параметром.
Пусть дано векторное дифференциальное уравнение
˙x = εA(t)x, x ∈ R
n
, t ∈ [0, +∞), (9)
где ε > 0 — малый параметр, а матрица–функция A(t) ограничена и
непрерывна на промнежутке [0, +∞), и удовлетворяет условию
Z
t
0
A(s) ds = tA
0
+ Q(t), (10)
причем A
0
— постоянная матрица, kQ(t)k ≤ m для всех t ∈ [0, +∞)
(m > 0 — константа).
Следующая теорема принадлежит В.А.Якубовичу.
Теорема 2. Пусть в усредненной системе ˙x = εA
0
x (x ∈ R
n
)
матрица A
0
гурвицева. Тогда система (9) экспоненциально устой-
чива при 0 ≤ ε ≤ ε
0
, где ε
0
— достаточно малое число.
Д о к а з а т е л ь с т в о . Рассмотрим матрицу
R
ε
(t) = I
n
+ εQ(t), (11)
где Q(t) — ограниченная матрица, удовлетворяющая условию (10)
(I
n
— единичная (n × n)-матрица). Легко показать, что
det R
ε
(t) = 1 + ε · Tr Q(t) +
n
X
k=2
α
k
(t)ε
k
, (12)
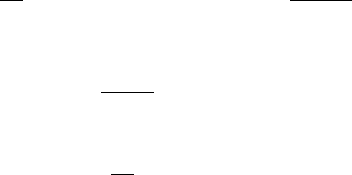
233
где α
k
(t) — некоторые ограниченные функции на [0, +∞). Действи-
тельно, пусть λ
j
(t), (j = 1, ··· , n) — собственные числа матрицы
Q(t) с учетом их кратностей. Тогда собственные числа матрицы R
ε
(t)
равны 1 + ελ
j
(t), (j = 1, ··· , n). Поскольку определитель матрицы
R
ε
(t) равен произведению собственных чисел, то
det R
ε
(t) =
n
Q
j=1
(1 + ελ
j
(t)) = 1 + ε
n
P
j=1
λ
j
(t)+
+ε
2
P
1=j
1
<j
2
=n
λ
j
1
(t)λ
j
2
(t) + ··· + ε
n
(λ
1
(t) ···λ
n
(t)).
(13)
Так как сумма собственных чисел
n
P
j=1
λ
j
(t) равна следу матрицы
Q(t), то из (13) следует (12), где
α
k
(t) =
X
1=j
1
<···<j
k
=n
λ
j
1
(t) ···λ
j
k
(t) (k = 2, ··· , n).
причем α
k
(t) — ограниченные функции, так как матрица Q(t) огра-
ничена и, следовательно, ограничены λ
j
(t).
Из равенства (12) следует, что при достаточно малом ε
1
> 0
det R
ε
(t) > 1 − δ > 0 (14)
при 0 ≤ ε ≤ ε
1
и всех t ∈ [0, +∞), где δ > 0 — некоторое положи-
тельное число.
Сделаем в системе (9) замену переменных
x = R
ε
(t)y, τ = εt (y ∈ R
n
), (15)
где R
ε
(t) — матрица (11).
Имеем
dy
dt
= (R
ε
(t))
−1
·
εA(t)R
ε
(t) −
dR
ε
(t)
dt
¸
y.
Отсюда, учитывая равенства (11) и
dQ(t)
dt
= A(t) −A
0
,
и переходя к новому времени τ, получаем
dy
dτ
= A
0
y + z(τ), (16)
где
z(τ ) = ε(R
ε
(t))
−1
[A(t)Q(t) − Q(t)A
0
]y(τ). (17)

234
Заметим, что поскольку матрица R
ε
(t) ограничена и удовлетворя-
ет условию (14), то преобразование (15) сохраняет свойство экспо-
ненциальной устойчивости, т.е. из устойчивости (экспоненциальной)
системы (9) следует устойчивость (экспоненциальная) системы (16),
(17) и, наоборот.
Будем искать функцию Ляпунова для системы (16), (17) в виде
квадратичной формы
V (y) = y
∗
P y, (18)
где симметрическая матрица P = P
∗
подлежит определению
Вычислим производную функции V (y) в силу системы (16), (17):
dV
dτ
= ˙y
∗
P y + y
∗
P ˙y = y
∗
(A
∗
0
P + P A
0
)y + 2y
∗
P z. (19)
Пусть G = G
∗
< 0 — произвольная отрицательно определенная мат-
рица. Тогда, поскольку по условию теоремы 2 матрица A
0
гурвицева,
то по лемме 1 из § 7, гл.III существует положительно определенная
матрица P = P
∗
> 0 такая, что
A
∗
0
P + P A
0
= G (G < 0). (20)
Так как матрицы A(t) и Q(t) ограничены, то, очевидно, ограничена
также и матрица
K
ε
(t) = (R
ε
(t))
−1
[A(t)Q(t) − Q(t)A
0
].
Пусть
kK
ε
(t)k ≤ M при 0 ≤ ε ≤ ε
1
, t ∈ [0, +∞).
Отсюда и из (17) имеем
kz(τ )k ≤ εMky(τ)k.
Учитывая последнее неравенство и равенство (20), из (19) получаем
следующую оценку
dV
dτ
≤ y
∗
Gy + 2εMkP k· kyk
2
или
dV
dτ
≤ y
∗
(G + 2εMkP kI
n
)y. (21)
Так как G > 0, то существует такое число ε
0
= ε
0
(G), 0 < ε
0
≤ ε
1
,
что
G + 2εMkP kI
n
< 0 при 0 ≤ ε ≤ ε
0
. (22)

235
Отсюда и из оценки (21) следует, что функция V (y) из (18) удо-
влетворяет всем условиям теоремы 1. Следовательно, по теореме 1,
с учетом предложения 2, система (16), (17) и, значит, система (9)
экспоненциально устойчива (при t → +∞) при 0 ≤ ε ≤ ε
0
. Теорема
2 доказана.
Замечание 1. Поскольку значение ε
0
(G), найденное из условия
(19), зависит от выбора матрицы G, то возникает естественная за-
дача о максимизации ε
0
(G) по всем G < 0. Последняя задача ре-
шена В.А.Якубовичем. Приведем без доказательства этот результат:
в условиях теоремы 2 система (9) экспоненциально устойчива при
0 < ε < ε
∗
(≤ ε
1
), где
ε
∗
= min(ε
1
, ε
∗∗
), ε
∗∗
= M
−1
inf
ω∈R
inf
keyk=1
k(iωI
n
− A
0
)eyk;
при этом ε
∗
≥ sup
G<0
ε
0
(G).
Замечание 2. Как это легко видеть из доказательства теоремы
2, экспоненциальная устойчивость системы (9) будет равномерной
относительно ε ∈ [0, ε
0
].
3. Экспоненциальная устойчивость линейной системы с
большим параметром.
Рассмотрим теперь дифференциальное уравнение
˙x = A(ωt)x, x ∈ R
n
, t ∈ [0, +∞), (23)
с непрерывной и периодической с периодом T > 0 матричнозначной
функцией A : R → R
n×n
: τ → A(τ ), A(τ + T ) = A(T), где ω > 0 —
большой параметр.
Систему (23) иногда называют системой с быстрым временем.
Из доказанной выше теоремы 2 следует
Теорема 3. Если усредненная система
˙x = A
0
x, x ∈ R
n
,
где
A
0
=
1
T
Z
T
0
A(τ) dτ, (24)
236
асимптотически устойчива (т.е. матрица A
0
— гурвицева), то си-
стема (23) равномерно экспоненциально устойчива для всех
ω ≥ ω
0
, где ω
0
— достаточно большое положительное число.
Д о к а з а т е л ь с т в о . Заменой времени ωt → t система (23)
легко сводится к системе
˙x = εA(t)x, A(t + T ) = A(t), x ∈ R
n
, t ∈ [0, +∞), (25)
с малым параметром ε > 0, где ε = 1/ω.
Система (25) — частный случай системы (9), рассмотренной в п.2.
Действительно, матрица A(t), очевидно, непрерывна и ограничена на
[0, +∞). Далее, представляя любое t > 0 в виде t = nT +s, 0 ≤ s < T
и учитывая периодичность матрицы A(t) будем иметь:
t
Z
0
A(τ) dτ =
nT
Z
0
A(τ) dτ +
s
Z
0
A(τ) dτ = n
T
Z
0
A(τ) dτ +
s
Z
0
A(τ) dτ =
= (nT + s)A
0
+
s
Z
0
[A(τ) − A
0
] dτ = tA
0
+ Q(t),
где
Q(t) =
t−nT
Z
0
[A(τ) − A
0
] dτ
матрица–функция, ограниченная на [0, +∞), поскольку
0 ≤ t − nT < T .
Согласно теореме 2 и замечания к ней система (25) равномерно
экспоненциально устойчива для всех ε ∈ [0, ε
0
], где ε
0
> 0, достаточ-
но мало, если матрица A
0
из (24) гурвицева. Отсюда следует утвер-
ждение теоремы 5.
§ 3. Высокочастотная стабилизация верхнего
положения равновесия маятника
Как и в гл.IV мы начнем с классической задачи стабилизации верх-
него положения равновесия маятника, но в отличие от § 3 гл.IV, по-
кажем возможность его высокочастотной стабилизации.
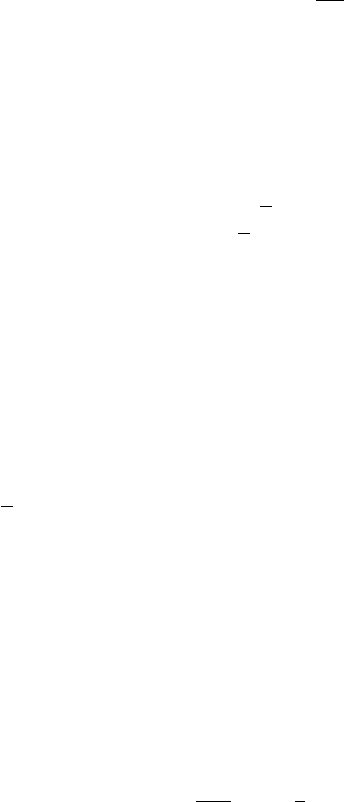
237
В § 3, гл.IV нами было получено уравнение малых колебаний (урав-
нение в вариациях) маятника около верхнего положения равновесия
с вибрирующей точкой подвеса. Оно имеет вид
¨
θ + α
˙
θ + (s(t) − ν
2
0
)θ = 0, (1)
где θ — угол отклонения, отсчитываемый от верхнего положения рав-
новесия, α — коэффициент трения, ν
0
=
p
g/` — собственная частота
малых колебаний (` — длина маятника, g — ускорение свободного па-
дения), s(t) = w(t)/`, w(t) — ускорение точки подвеса.
Будем рассматривать два различных класса стабилизирующих фу-
нкций s(t), а именно, кусочно-постоянные периодические функции
(с нулевым средним на периоде) с достаточно малым периодом T
([16,17])
s(t) =
½
−β при t ∈ [0,
T
2
],
β при t ∈ [
T
2
, 0),
s(t + T ) = s(t), (2)
и непрерывные периодические функции вида ([259,260])
s(t) = s
0
+ βω cos ωt (или s(t) = s
0
+ βω
2
cos ωt), (3)
где s
0
, β и ω — варьируемые параметры (ω — большой параметр).
1. Стабилизация с помощью кусочно-постоянных перио-
дических функций ([16,17]). Рассмотрим сначала стабилизацию
верхнего положения равновесия маятника с помощью функций ви-
да (2). Пусть амплитуда колебаний точки подвеса равна a(a ¿ `), а
ускорение w(t) точки подвеса постоянно в течение каждого полупе-
риода τ =
T
2
и равно
w(t) =
½
−c при t ∈ [0, τ),
c при t ∈ [τ, T ),
w(t + T ) = w(t) ∀t ∈ [0, +∞),
где c > 0 — константа.
Эквивалентная уравнению (1) система уравнений первого при-
ближения в окрестности верхнего положения равновесия имеет вид
(θ := x
1
):
½
˙x
1
= x
2
,
˙x
2
= −αx
2
− (s(t) − ν
2
0
)x
1
.
(4)
Очевидно, что
a =
cT
2
32
, β =
c
`
,
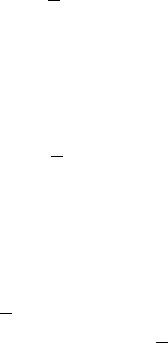
238
где β — варьируемый параметр в (2).
Еcли колебания точки подвеса достаточно быстры, то
β > ν
2
0
(так как β = 32a/`T
2
и T достаточно мало).
Пусть H — преобразование за время от 0 до T , осуществляемое
фазовым потоком системы (4). Очевидно, что преобразование H со-
стоит из произведения двух преобразований: H = H
2
H
1
, где H
1
—
преобразование за время от 0 до
T
2
, осуществляемое фазовым пото-
ком {f
t
} системы
½
˙x
1
= x
2
,
˙x
2
= −αx
2
+ (β + ν
2
0
)x
1
,
(5)
(положение равновесия (x
1
= 0, x
2
= 0) — седло) т.е. H
1
= f
τ
0
, а H
2
есть преобразование за время от
T
2
до T , осуществляемое фазовым
потоком {g
t
} системы
½
˙x
1
= x
2
˙x
2
= −αx
2
− (β −ν
2
0
)x
1
,
(6)
(положение равновесия (x
1
= 0, x
2
= 0) — фокус) т.е. H
2
= g
T
τ
(снача-
ла в промежутке времени [0,
T
2
] точки плоскости движутся по траек-
ториям системы (5), а затем в промежутке [
T
2
, T ] — по траекториям
системы (6)). Поскольку система (6) автономная и, следовательно,
сдвиг решения (вдоль оси t ) есть решение, то
H
2
= g
T
τ
= g
τ
0
.
Найдем матрицы преобразований H
1
и H
2
(очевидно H
1
и H
2
—
линейные операторы).
В силу предложения 1 из § 3, гл.IV
H
1
= Ψ
1
(τ), H
2
= Ψ
2
(τ),
где Ψ
1
(t) и Ψ
2
(t) — нормированные фундаментальные матрицы ре-
шений систем (5) и (6) соответственно (Ψ
i
(0) = I, i = 1, 2).
Вычислим Ψ
1
(t) и Ψ
2
(t).
Общее решение системы (5) имеет вид
½
x
1
(t) = c
1
e
λ
1
t
+ c
2
e
λ
2
t
,
x
2
(t) = c
1
λ
1
e
λ
1
t
+ c
2
λ
2
e
λ
2
t
,
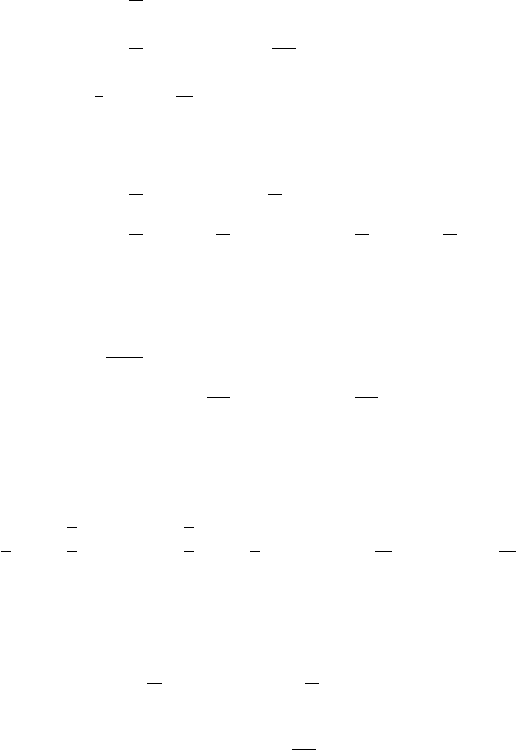
239
где λ
1
, λ
2
— корни характеристического уравнения p
2
+αp−(β+ν
2
0
) =
0 системы (5):
λ
1
= −
α
2
+ k,
λ
2
= −
α
2
− k, k
2
=
α
2
4
+ (β + ν
2
0
).
Обозначим ρ(t) =
1
2
exp
¡
−
αt
2
¢
.
Частное решение системы (5) с начальным условием x
1
(0) = 1,
x
2
(0) = 0:
x
1
(t) = ρ(t)
h³
1 +
α
k
´
e
kt
+
³
1 −
α
k
´
e
−kt
i
,
x
2
(t) = ρ(t)
h³
1 +
α
k
´³
k −
α
2
´
e
kt
−
³
1 −
α
k
´³
k +
α
2
´
e
−kt
i
.
Частное решение системы (5) с начальным условием x
1
(0) = 0,
x
2
(0) = 1:
x
1
(t) =
ρ(t)
k
¡
e
kt
− e
−kt
¢
,
x
2
(t) = ρ(t)
h³
1 −
α
2k
´
e
kt
+
³
1 +
α
2k
´
e
−kt
i
.
Теперь, составляя фундаментальную матрицу Ψ
1
(t) из найденных
частных решений и полагая в ней t = τ , получим
Ψ
1
(τ) =
= ρ
τ
µ
(1 +
α
k
)e
kτ
+ (1 −
α
k
)e
−kτ
2k
−1
sh kτ
(1 +
α
k
)(k −
α
2
)e
kτ
− (1 −
α
k
)(k +
α
2
)e
−kτ
(1 −
α
2k
)e
kτ
+ (1 +
α
2k
)e
−kτ
¶
.
(Здесь sh — гиперболический синус, ρ
τ
= ρ(τ)).
Характеристическое уравнение p
2
+ αp + (β − ν
2
0
) = 0 системы (6)
имеет комплексно-сопряженные корни
λ
0
1
= −
α
2
+ iΩ, λ
0
2
= −
α
2
− iΩ,
Ω
2
= (β − ν
2
0
) −
α
2
4
,
если
α
2
< 4(β − ν
2
0
)
(последнее условие выполнено, если колебания точки подвеса маят-
ника достаточно быстры).

240
Общее решение системы (6):
½
x
1
(t) = 2ρ(t)(c
1
cos Ωt + c
2
sin Ωt),
x
2
(t) = 2ρ(t) [(c
2
Ω − c
1
α/2) cos Ωt − (c
2
α/2 + c
1
Ω) sin Ωt] .
Находим частные решения системы (6) с начальными условиями
x
1
(0) = 1, x
2
(0) = 0 и x
1
(0) = 0, x
2
(0) = 1. Ими будут соответствен-
но:
½
x
1
= 2ρ(t)(cos Ωt +
α
2Ω
sin Ωt),
x
2
= −2(Ω +
α
2
4Ω
)ρ(t) sin Ωt;
½
x
1
= 2Ω
−1
ρ(t) sin Ωt,
x
2
= 2ρ(t)
¡
cos Ωt −
α
2Ω
sin Ωt
¢
.
Составляем фундаментальную матрицуΨ
2
(t) и полагаем в ней t = τ.
Получим :
Ψ
2
(τ) = 2ρ
τ
µ
cos Ωτ +
α
2Ω
sin Ωτ Ω
−1
sin Ωτ
−(Ω +
α
2
4Ω
) sin Ωτ cos Ωτ −
α
2Ω
sin Ωτ
¶
.
В силу теоремы 4 из § 2, гл.IV преобразование H за время T асимпто-
тически устойчиво тогда и только тогда, когда собственные значения
(мультипликаторы) ρ
1
и ρ
2
матрицы
Ψ(T ) = Ψ
1
(τ) · Ψ
2
(τ) (τ =
T
2
),
преобразования H находятся внутри единичного круга:
|ρ
j
| < 1, j = 1, 2.
Для упрощения выкладок предположим, что трение в системе (4)
отсутствует, т.е.α = 0. Тогда очевидно, что
det Ψ(T ) = 1,
и мы можем воспользоваться теоремой 6 из § 2, гл.IV.
Условие устойчивости
|T r Ψ(T )| < 2
принимает вид
|2 cos Ωτ · ch kτ + (k/Ω − Ω/k) sin Ωτ · sh kτ | < 2 (7)
(Здесь sh и ch — гиперболические синус и косинус соответственно).
Введем безразмерные переменные ε и δ:
ε
2
=
a
`
¿ 1, δ
2
=
g
c
¿ 1.
