Леонов Г.А., Шумафов М.М. Проблемы стабилизации линейных управляемых систем

Подождите немного. Документ загружается.

211

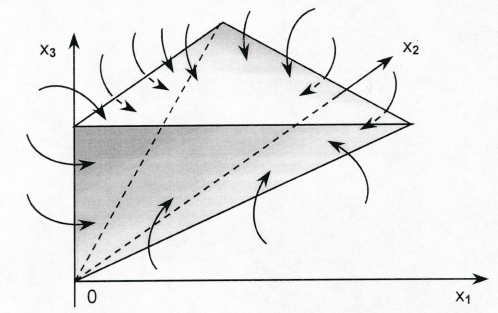
Рис.22. (Случай n = 3). Положительно инвариантное множество Ω.

Пусть решение x(t) системы (3) пересекает границу (размерности

n − 1)

∂Ω

= {x

= 0, x

> 0 ∀i 6= j , x

+ c

n−1

+ ··· + c

> 0}

(i, j = 1, ··· , n − 1)

множества Ω в момент t = τ , т.е. x(τ) ∈ ∂Ω

. Тогда

˙x

(τ) > 0. (4)

Действительно, при j = 1, 2, . . . , n − 2 имеем

˙x

(τ) = x

j+1

(τ) > 0.

При j = n − 1 (и n > 2)

˙x

n−1

(τ) = x

(τ) > −c

n−1

(τ) − ··· − c

(τ) ≥ 0,

так как c

≤ 0 (k = 1, . . . , n − 1) в силу условия 1) теоремы 1.

При n = 2 имеем

˙x

(τ) = x

(τ) > −c

(τ) ≥ 0

(так как c

≤ 0). Пусть теперь x(τ ) ∈ ∂Ω

, где

∂Ω

= {x

> 0 (j = 1, . . . , n − 1), x

+ c

n−1

+ ··· + c

= 0}

— оставшаяся (n − 1)-мерная граница множества Ω. Обозначим

V (x) = x

+ c

n−1

+ ··· + c

212

Тогда в силу системы (3) имеем

dV (x(t))

t=τ

= −a

− ··· − a

+ c

n−1

+ ··· + c

= (c

n−1

− a

(τ) + ··· + (c

− a

(τ) − a

= (c

n−1

− a

)(−c

n−1

(τ) − ··· − c

(τ))+

+ ··· + (c

− a

(τ) − a

(τ) =

= [−a

n−1

+ c

n−2

+ c

n−1

− c

n−1

(τ) + ···

··· + [−a

+ c

− c

n−1

(τ)+

+[−a

+ c

− c

n−1

)]x

(τ)

(здесь мы использовали соотношение x

(τ) + c

n−1

(τ) + ··· +

(τ) = 0). Отсюда и из условия 2) теоремы 1 следует неравен-

ство

dV (x(t))

t=τ

> 0. (5)

Из неравенств (4) и (5) следует, что граница ∂Ω множества Ω,

за исключением ее частей, имеющих размерность не больше, чем

n − 2, является бесконтактной по отношению к векторному полю,

определяемому системой (3) и решения системы (3) "прошивают"эту

границу снаружи вовнутрь множества Ω. Отсюда и из непрерывной

зависимости решений системы (3) от начальных данных следует по-

ложительная инвариантность множества Ω.

Так как ˙x

> 0 внутри множества Ω, то из положительной инвари-

антности Ω вытекает, что нулевое решение x(t) ≡ 0 и, следовательно,

сама система (3) не является асимптотически устойчивой ни при ка-

ком выборе функции s(t). Теорема 1 доказана.

Таким образом, необходимым условием стабилизации системы

(1) является нарушение хотя бы одного из условий 1) или 2) тео-

ремы 1.

Приведем теперь другое хорошо известное [16,17] достаточное усло-

вие неустойчивости системы вида (2).

Теорема 2. Если для линейной системы

˙x = P (t)x, t ∈ R, x ∈ R

, (6)

с кусочно–непрерывной матрицей P (t) выполнено неравенство

T r P (t) ≥ α > 0 ∀t ∈ R (7)

для некоторого положительного числа α, то система (6) неустой-

чива.

213

Если вместо условия (7) выполнено неравенство

T r P (t) ≥ 0,

то система (6) не является асимптотически устойчивой.

Д о к а з а т е л ь с т в о . Пусть

, . . . , η

— произвольная система линейно независимых векторов фазового

пространства R

(t) = ψ

(t; η

, t

), . . . , ψ

(t) = ψ

(t; η

, t

)

— фундаментальная система решений уравнения (6) (см. следствие

2 теоремы 1 из § 2), выходящих в момент t = t

из векторов {η

}

k=1

) = η

, . . . , ψ

) = η

Пусть W (t) – определитель Вронского фундаментальной матрицы

Ψ(t) решений {ψ

(t)}

k=1

W (t) = det Ψ(t), Ψ(t) = (ψ

(t), ··· , ψ

(t)).

Тогда по теореме Лиувилля

W (t) = W (t

) exp

T r P (τ ) dτ

и, следовательно, в силу условия (7)

|W (t)| ≥ |W ( t

)|e

α(t−t

)

. (8)

Если система (6) была бы устойчивой, то для любого наперед задан-

ного шара S

(с центром в начале координат) радиуса ε (ε > 0 —

произвольное число) существовал бы шар S

радиуса δ такой, что

преобразование g

фазового пространства R

, осуществляемое тра-

екториями уравнения (6) за время от t

до t, переводило бы шар

(с центром в начале координат) в множество g

, лежащее при

любом t ≥ t

в шаре S

, т.е.

⊂ S

∀t ∈ [t

, +∞). (9)

214

≡ S

, напомним, что (см. п.1, § 2) g

= ψ(t; x

, t

)), где

ψ(t; x

, t

) — решение уравнения (6) с начальным условием

ψ(t

; x

, t

) = x

). Из (9) имеем:

µ(g

) ≤ µ(S

) ≤ C

, (10)

где C

— некоторая константа (зависящая от размерности фазового

пространства), µ — мера соответствующего множества.

Возьмем теперь длины векторов

, . . . η

настолько малыми, что-

бы параллелепипед Σ

, натянутый на векторы η

, . . . , η

, лежал в

шаре S

: Σ

⊂ S

. Так как g

: R

→ R

линейное преобразование

(см. следствие 3 теоремы 1 из § 2), то образ g

параллелепипеда

тоже есть параллелепипед Σ

, объем µ(Σ

) которого равен

µ(Σ

) = |det (g

, . . . , g

)| = |det Ψ(t)| = |W (t)|, (11)

т.е. значению в момент t модуля определителя Вронского.

Поскольку Σ

⊂ S

, то в силу (9)

⊂ S

(Σ

= g

) ∀t ≥ t

и, поэтому, используя (10), (11), получаем

|W (t)| = µ(Σ

) ≤ C

∀t ≥ t

Отсюда следует, что функция |W (t)| ограничена на промежутке

, +∞). С другой стороны, из соотношения (8) следует, что

|W (t)| → +∞ при t → +∞. Полученное противоречие доказывает

первую часть теоремы 2.

Вторая часть теоремы 2 доказывается аналогично. Действительно,

асимптотическая устойчивость системы (6) означала бы, что кроме

условия (9), для векторов η

, . . . , η

∈ R

выполняются еще соотно-

шения:

→ 0, . . . , g

→ 0

при t → +∞ и, следовательно, в силу (11)

|W (t)| → 0 при t → +∞

вопреки неравенству

|W (t)| ≥ |W (t

)|,

которое следует из формулы Лиувилля в силу условия T r P (t) ≥ 0.

Теорема 2 доказана полностью.

215

Следствие. Система (2) неустойчива, если

T r (A + s(t)bc

∗

) ≥ α > 0 ∀t ∈ R

(α – некоторое число), и не является асимптотически устойчивой,

если

T r (A + s(t)bc

∗

) ≥ 0 ∀t ∈ R.

§ 9. Низкочастотная стабилизация двумерных

и трехмерных систем

Применим полученные в предыдущих параграфах результаты к

двумерным и трехмерным системам.

1. Двумерные системы. Рассмотрим систему со скалярным вхо-

дом u(t) и скалярным выходом y(t), передаточная функция которой

равна

W (p) =

p + c

+ a

p + a

, (1)

где a

, a

; c

, c

— некоторые вещественные числа.

Будем предполагать, что c

6= 0. Тогда, не умаляя общности, мож-

но считать, что c

= 1. Предположим также, что функция W (p)

невырождена, т.е.

− a

+ a

6= 0. (2)

Тогда систему с передаточной функцией (1) можно реализовать (в

силу следствия теоремы 2 из § 3, гл.II) в фазовом пространстве R

как систему вида (1) из § 1:

˙x

= x

˙x

= −a

− a

− u, y = c

+ x

(3)

Здесь

A =

0 1

−a

, b =

−1

, c =

, x =

Из условий Рауса–Гурвица (см. § 2, гл.III)вытекает, что стационар-

ная стабилизация системы (2) с помощью обратной связи

u = s

y, s

= const 6= 0 возможна тогда и только тогда, когда

+ s

> 0, a

+ c

> 0.

216

Легко вывести, что для существования числа s

, удовлетворяющего

последним неравенствам, необходимо и достаточно выполнения либо

условия c

> 0, либо соотношений c

≤ 0, a

< a

Рассмотрим случай, когда стационарная стабилизация невозмож-

на:

≤ 0, a

≥ a

. (4)

Применим теорему из § 5 к системе (3). Условие 1) этой теоремы

выполнено для s

6= 0:

det bs

∗

= s

det bc

∗

= 0

T r bs

∗

= s

T r bc

∗

= s

∗

b = −s

6= 0.

Условие 2) этой же теоремы будет выполнено, если при некотором

∈ R характеристический многочлен

+ (a

+ σ

)p + (a

+ c

)

системы (2), где u = σ

y имеет комплексно сопряженные корни. Лег-

ко видеть, что для существования такого числа σ

необходимо и до-

статочно выполнения неравенства

− a

+ a

> 0. (5)

Таким образом, если выполнено неравенство (5), то в силу теоремы

из § 5 существует такая обратная связь u = s(t)y, где s(t) — кусочно-

постоянная периодическая функция, что система (3), где u = s(t)y,

асимптотически устойчива.

Этот же результат можно получить и с помощью теоремы 2 из § 7.

Для этого, не умаляя общности, можно предположить, что a

> 0.

Этого всегда можно достичь выбором s

в выражении (правой части

второго уравнения системы (3), где u = s(t)y)

−(a

+ s

− (a

+ c

− (s(t) − s

)(c

+ x

)

и переобозначениями

+ s

→ a

, a

+ c

→ a

, s(t) − s

→ s(t).

Заметим, что, тогда из условия (2) и неравенств (4) вытекает, что

> 0.

Из неравенства a

> 0 и соотношений (4) следует, что матрица A

в системе (2) имеет вещественные собственные числа −λ и κ разных

217

знаков: −λ < 0, κ > 0, причем λ > κ (так как −λ + κ = −a

< 0).

Далее, условие (13) в теореме 2 (§ 7) принимает здесь вид

κ + λ

κ + c

< 1.

(В силу (2) κ 6= −c

Отсюда получаем, что все условия теоремы 2 из § 7 выполнены,

если

(λ − c

)(κ + c

) = −c

+ a

− a

< 0.

Это неравенство совпадает с неравенством (5).

Если выполнено неравенство

− a

+ a

< 0,

то, как легко видеть, выполнены условия теоремы 1 из § 8 и, тем

самым, система (3) не может быть стабилизируема ни при какой

обратной связи u = s(t)y.

Итак, нами получен следующий результат.

Теорема 1. Пусть передаточная функция W (p) системы (3) невы-

рождена, т.е. выполнено неравенство (2).

Тогда необходимым и достаточным условием стабилизируемо-

сти системы (3) является выполнение хотя бы одного из условий:

1) c

> 0 или 2) c

≤ 0, c

− a

+ a

> 0. (6)

При этом в стабилизирующем управлении u = s(t)y, функцию s(t)

можно выбрать кусочно-постоянной периодической с достаточно

большим периодом (низкочастотная стабилизация).

Замечание 1. В следующей главе V будет показано с помощью

процедуры усреднения, что условия 1), 2) теоремы 1 также необхо-

димы и достаточны в другом классе стабилизирующих функций s(t)

вида

s(t) = s

+ s

ω cos ωt (s

, s

∈ R),

где ω — достаточно большое число (высокочастотная стабилизация).

218

Замечание 2. Теорема 1 очень хорошо иллюстрирует как введе-

ние функции s(t) 6≡ s

, s

= const, в обратной связи u = s(t)y (неста-

ционарная стабилизация) расширяет возможности стационарной ста-

билизации (s(t) ≡ s

): в пространстве параметров {(a

, a

; c

)} си-

стемы (3) условия (6) выделяют более широкую область, чем об-

ласть, определяемая условиями Рауса-Гурвица (c

> 0 или c

≤ 0,

< a

) при стационарной стабилизации.

2. Трехмерные системы.

1) Пусть передаточная функция системы (3) со скалярным входом

u(t) и скалярным выходом y(t) имеет вид:

W (p) =

+ αp

+ βp + γ

, (7)

где α, β, γ — некоторые вещественные числа. (Очевидно, функция

W (p) невырождена). Тогда такую систему (в силу следствия теоремы

2 из § 3 гл.II) можно реализовать в фазовом пространстве R

как

систему вида (1) из § 1:







˙x = x

˙x

= x

˙x

= −(αx

+ βx

+ γx

) − u, y = x

(8)

Стационарная стабилизация u = s

y системы (8) возможна тогда

и только тогда, когда

α > 0 и β > 0.

(это следует из условий Рауса–Гурвица).

Пусть α > 0, β ≤ 0 (в этом случае стационарная стабилизация

невозможна). Применим здесь теорему 4 из § 7.

Выберем σ

> 0 так, чтобы характеристический многочлен систе-

мы (8), где u = σ

y, имел вид:

+ αp

+ βp + (γ + σ

) = (p − κ

)(p

+ α

p + β

где α

= α + κ

, β

= β + κ

(α + κ

), κ

< 0, причем

= −κ

(α + κ

) − βκ

− γ.

219

При достаточно большом σ

и, значит, — κ

многочлен p

+ α

p + β

имеет два комплексных корня λ

± iω

, где λ

> 0, а исходный ха-

рактеристический многочлен — один отрицательный κ

и два ком-

плексных корня λ

± iω

Аналогично, возьмем s

< 0 так, чтобы характеристический мно-

гочлен системы (8), где u = s

y, принял вид:

+ αp

+ βp + (γ + s

) = (p − κ

)(p

+ α

p + β

где α

= α + κ

, β

= β + κ

(α + κ

), κ

> 0, причем

= −κ

(α + κ

) − βκ

− γ.

При достаточно большом |s

| и, значит, κ

многочлен p

+ α

p + β

имеет два комплексных корня −λ

±iω

, где λ

= (α + κ

)/2, причем

> 0, а характеристический многочлен — один положительный и

два комплексных корня −λ

± iω

Наконец, аналогично как и выше, возьмем s

настолько большим,

чтобы для характеристического многочлена системы (8), где u = s

выполнялось равенство

+ αp

+ βp + (γ + s

) = (p + λ

)(p

+ α

p + β

где α

= α − λ

, β

= β − λ

(α − λ

), и, тем самым, этот многочлен

при достаточно большом λ

будет иметь один отрицательный корень

−λ

< 0 и два комплексных корня κ

±iω

, причем κ

(λ

−α)

> 0.

Таким образом, здесь (см. теорему 4 из § 7)

dim M

= dim L

= 1, dim M

= dim L

= 2

α + κ

, κ

− α

− κ

α(λ

+ κ

) > 0.

Следовательно, выполнены все условия теоремы 4 из § 7. Поэтому

при α < 0, β ≤ 0 существует такое управление u = s(t)y, где s(t) —

кусочно-постоянная периодическая функция с достаточно большим

периодом, что система (8), где u = s(t)y, асимптотически устойчива.

Поскольку для системы (8) (u = s(t)y)

T r (A + bs(t)

∗

) = −α ∀t ∈ R,

то в силу теоремы 2 из § 8 система (8) (u = s(t)y) не является асимп-

тотически устойчивой при α ≤ 0.

Таким образом, получаем следующий результат.

220

Теорема 2. Система (8) с передаточной функцией (7) стабили-

зируема тогда и только тогда, когда α > 0. При этом функцию s(t)

в стабилизирующем управлении u = s(t)y можно выбрать кусочно-

постоянной периодической с достаточно большим периодом (низ-

кочастотная стабилизация).

Замечание 1. В гл.V будет показана возможность высокочастот-

ной стабилизации системы (8) в другом классе функций вида

s(t) = s

+ s

cos ωt (s

, s

∈ R),

где ω — достаточно большое число. При этом оказывается, что, как

и здесь, условие α > 0 необходимо и достаточно для стабилизируе-

мости системы (8).

Замечание 2. Как и теорема 1, теорема 2 хорошо иллюстриру-

ет преимущества нестационарной стабилизация (условие α > 0) по

сравнению со стационарной (условия α > 0, β > 0).

2) Рассмотрим систему со скалярным входом u(t) и скалярным

выходом y(t) и передаточной функцией вида

W (p) =

+ αp

+ βp + γ

где α, β и γ — некоторые вещественные числа. Будем считать, что

γ 6= 0 (условие невырожденности функции W (p)). Тогда эту систе-

му можно реализовать (в силу следствия теоремы 2 из § 3, гл.II) в

фазовом пространстве R

как систему







˙x

= x

˙x

= x

˙x

= −(αx

+ βx

+ γx

) − u, y = x

(9)

Из условий Рауса–Гурвица выводим, что стационарная стабилизация

u = s

y системы (9) возможна в том и только том случае, когда

α > 0, γ > 0.

Рассмотрим случай α > 0, γ < 0 (тогда стационарная стабилизация

невозможна). Применим здесь теорему 1 из § 7 с

= s

; λ

= λ

= λ, κ

= κ

= κ.