Леонов Г.А., Шумафов М.М. Проблемы стабилизации линейных управляемых систем

Подождите немного. Документ загружается.

201

При этом b

6= 0, c

6= 0. Действительно, если бы b

= 0, то

b =

; Ab =

, A

b =

, ··· , A

n−1

b =

n−1

и, следовательно, не выполнялось бы свойство (I

) полной управля-

емости пары (A, b). Аналогично, если бы c

= 0, то

c =

; A

∗

c =

∗

, (A

∗

)

c =

∗

)

, ··· , (A

∗

)

n−1

c =

∗

)

n−1

и, стало быть, не выполнялось бы свойство полной наблюдаемости

пары (A, c). Значит, h

∗

b 6= 0 и c

∗

d 6= 0.

Следовательно, по лемме 2 существуют числа µ и τ(µ) такие, что

для системы (1) выполнено соотношение (см. рис.19)

∗

x(τ(µ); d) = 0,

и, следовательно, включение θ

τ(µ)

M ⊂ L ("условие вложения много-

образий"из § 4), если

∗

< 1.

Последнее неравенство обеспечивается условием (13) теоремы 2.

Действительно, для этого достаточно заметить, что передаточная

функция W (p) = c

∗

(A − pI

)

−1

b имеет вид:

W (p) = (c

, c

∗

)

(κ − p)

−1

0 D(p)

¶µ

κ − p

+ c

∗

D(p)b

( где D(p) = (A − pI

n−1

)

−1

и, поэтому,

lim

κ→p

(κ − p)W (p) = b

Так как λ > κ, то выполнены все условия основной теоремы из § 4,

и, следовательно, система (12) асимптотически устойчива. Теорема

2 доказана.

Теорема 3. Предположим, что c

∗

b 6= 0 и существуют числа

6= s

такие, что:

1) матрица A + s

∗

имеет положительное собственное значе-

ние κ

;

202

2) матрица A + s

∗

имеет одно положительное собственное

значение κ

и n −1 собственное значение с отрицательными веще-

ственными частями;

3) выполнено условие (7) основной теоремы из § 4;

4) имеет место неравенство

∗

− s

− κ

< 1.

Тогда существует периодическая функция s(t) вида (9) (§ 4) такая,

что система (12) асимптотически устойчива.

Д о к а з а т е л ь с т в о . Как и в доказательстве теоремы 2, не

умаляя общности, можно считать, что матрица A + s

∗

и векторы

b и c имеют вид

A + s

∗

0 A

, b =

, c =

где A

— гурвицева (n−1)×(n−1)-матрица; b

, c

∈ R; b

, c

∈ R

n−1

В этом случае вектор h, нормальный к подпространству L

, имеет

вид:

h = (1, 0 ···0)

∗

Рассмотрим ненулевой вектор d ∈ M

. Для этого вектора выпол-

нено соотношение

(A + s

∗

)d = κ

так как M

— инвариантное подпространство (прямая), определяе-

мое собственным значением κ

> 0 (d — соответствующий собствен-

ный вектор) матрицы A + s

∗

Последнее соотношение можно записать в виде

(A + s

∗

− κ

I)d = (s

− s

)b(c

∗

или

d = (s

− s

)(A + s

∗

− κ

−1

b(c

∗

d).

Из этого равенства, очевидно, вытекает, что c

∗

d 6= 0. Отсюда следует

равенство

∗

d = (s

− s

∗

(A + s

∗

− κ

−1

b(c

∗

d).

Поэтому условие

∗

< 1

203

леммы 2 записывается следующим образом:

∗

− s

∗

(A + s

∗

− κ

−1

∗

< 1.

С учетом того, что h

∗

b = b

, а матрица (A + s

∗

− κ

I) имеет вид

(A + s

∗

− κ

)

−1

(κ

− κ

)

−1

0 (A

− κ

n−1

)

−1

последнее неравенство перепишется так:

∗

− s

− κ

< 1.

Таким образом, выполнены все условия леммы 2 и, поэтому спра-

ведливо "условие вложения многообразий"(6) из § 4.

Следовательно, выполняются все условия основной теоремы (§ 4)

и, значит, система (12) асимптотически устойчива. Теорема 3 дока-

зана.

3. Случай размерности n − 2 (коразмерности 2) устойчи-

вого многообразия.

Выше условия асимптотической устойчивости системы (12) были

получены в предположении, что размерность устойчивого многооб-

разия — подпространства L

— равна n − 1 (т.е. когда L

— гипер-

плоскость в R

Приведем один результат, касающийся случая, когда dim L

= n−

2. Для этого сначала докажем следующую лемму.

Лемма 3. Пусть (n − 2)-мерное линейное подпространство L,

расположенное в гиперплоскости {h

∗

x = 0} (h ∈ R

, h 6= 0), явля-

ется интегральным многообразием для системы (1). Если выполне-

но равенство

∗

b = 0, (15)

то пара (A, h) полностью наблюдаема.

Д о к а з а т е л ь с т в о . Прежде всего заметим, что подпростран-

ство L ⊂ {h

∗

x = 0} инвариантно относительно оператора A + µbc

∗

так как L — инвариантное многообразие системы (1).

Из полной управляемости пары (A, b) и инвариантности подпро-

странства L относительно A + µbc

∗

следует, что b /∈ L.

204

Действительно, предположим противное: b ∈ L. Возьмем ненуле-

вой вектор h

⊥L. Тогда h

∗

b = 0. Из инвариантности L относительно

A + µbc

∗

вытекает (как и в доказательстве леммы 1 § 6), что

∗

(A + µbc

∗

)

x = 0, k = 1, 2 . . . (16)

для всех x ∈ L.

Полагая в (16) x = b и k = 1 получим

0 = h

∗

(A + µbc

∗

)b = h

∗

Ab,

так как h

∗

b = 0.

Отсюда и из (16) при k = 2, x = b имеем

0 = h

∗

(A + µbc

∗

)

b = h

∗

A(A + µbc

∗

)b = h

∗

Продолжая этот процесс далее получим, что h

∗

b = 0 при

k = 0, 1, . . . , n − 1. Отсюда следует (поскольку h

6= 0), что век-

торы b, Ab, ··· , A

n−1

b линейно зависимы, что противоречит полной

управляемости пары (A, b). Полученное противоречие доказывает,

что b /∈ L.

Следовательно, линейная оболочка L(b, L), натянутая на вектор b

и подпространство L, совпадает с гиперплоскостью {h

∗

x = 0}, так

как h

∗

b = 0, L ⊂ {h

∗

x = 0} и dim L = n − 2.

Предположим, что пара (A, h) неполностью наблюдаема. Тогда су-

ществуют (свойство (V I

),§ 1, гл.II) ненулевой вектор ξ ∈ C

= CR

и число λ ∈ C такие, что

∗

ξ = 0, Aξ = λξ (ξ 6= 0). (17)

Из полной наблюдаемости пары (A, c) следует неравенство c

∗

ξ 6= 0.

Так как подпространство L ⊂ R

инвариантно относительно

A + µbc

∗

, то (как и в доказательстве леммы 1 § 6) будем иметь соот-

ношения:

∗

(A + µbc

∗

)

x = 0, k = 1, 2, . . .

для всех x ∈ L. Отсюда вытекают равенства

∗

(A + µbc

∗

)

x = 0, k = 1, 2, . . . (18)

для всех z из комплексифицированного подпространства CL ⊂ {h

∗

z =

0} ⊂ CR

(z = x + iy, x, y, ∈ R

Легко видеть, что из того, что b /∈ L следует аналогичное соотно-

шение b /∈ CL и, поэтому L(b, CL) = {z ∈ CR

: h

∗

z = 0}.

205

Отсюда следует, что для вектора ξ ∈ {h

∗

z = 0} имеет место ра-

венство

ξ = η + νb, (19)

где η ∈ CL, ν ∈ C.

Если в (19) ν = 0, то, повторяя рассуждения доказательства лем-

мы 1 § 6, получим, что пара (A, h) наблюдаема.

Пусть ν 6= 0. С учетом (15) и (17), имеем

∗

(A + µbc

∗

)ξ = λh

∗

ξ + µh

∗

ξ = 0.

Отсюда, используя разложение (19) и учитывая (16), получаем

0 = h

∗

(A + µbc

∗

)ξ = h

∗

(A + µbc

∗

)η + νh

∗

(A + µbc

∗

)b = νh

∗

Ab,

так как h

∗

(A + µbc

∗

)η = 0 в силу (18) (k := 1). Следовательно,

∗

Ab = 0. Из последнего соотношения и равенств (15), (17), имеем

∗

(A + µbc

∗

)

ξ = h

∗

A(A + µbc

∗

)ξ =

= h

∗

ξ + µh

∗

Abc

∗

ξ = λ

∗

ξ = 0.

Отсюда, как и выше, используя (19) и равенства (15) и h

∗

Ab = 0,

получим

0 = h

∗

(A + µbc

∗

)

ξ = h

∗

(A + µbc

∗

)

η + νh

∗

(A + µbc

∗

)

b =

= νh

∗

A(Ab + µbc

∗

b) = νh

∗

так как

∗

(A + µbc

∗

)

η = 0

в силу (18) (k := 2).

Продолжая этот процесс далее, последовательно приходим к ра-

венствам

∗

b = 0, h

∗

Ab = 0, . . . , h

∗

n−1

b = 0,

которые означают, что пара (A, b) неполностью управляема. Полу-

ченное противоречие доказывает утверждение леммы 3. Лемма 3 до-

казана.

Применяя лемму 3, установим справедливость следующего утвер-

ждения.

Теорема 4. Пусть для системы (10) выполнены предположения

основной теоремы (§ 4), причем

dim M

= 1, dim L

= n − 2.

206

Пусть, далее, для некоторого числа σ

6= s

(j = 1, 2) матрица

A + σ

∗

имеет два комплексно сопряженных собственных значения α ± iβ

кратности 1, а остальные ее собственные значения λ

удовлетво-

ряют условию Re λ

< α.

Тогда существует периодическая функция s(t) вида (9)(§ 4), где

σ(t) ≡ σ

, s

, σ

∈ R, такая, что система (12) асимптотически

устойчива.

Д о к а з а т е л ь с т в о . Рассмотрим интегральное многооб-

разие Ω(µ), состоящее из траекторий x = ϕ(t; x

, µ) системы (1) с

начальными данными x

∈ L

, т.е.

Ω(µ) = {x ∈ R

: x = ϕ(t; x

, µ), x

∈ L

, t ∈ (t

, t

)},

где t

, t

— некоторые числа (t

< 0 < t

), ϕ(0; x

, µ) = x

Пусть h — вектор, нормальный к линейной оболочке L(b, L

), на-

тянутой на вектор b и подпространство L

. Тогда гиперплоскость

L(b, L

) = {h

∗

x = 0}

является интегральным многообразием системы

˙x = (bc

∗

)x, (20)

так как h

∗

(bc

∗

) = 0.

Поскольку система (1) имеет те же самые траектории, что и си-

стема

˙x =

A + bc

∗

а последняя сколь угодно близка к системе (20) при достаточно боль-

ших |µ|, то многообразие Ω(µ) приближается к гиперплоскости

∗

x = 0} при µ → +∞ ( рис.21):

Ω(µ) → {h

∗

x = 0} (µ → +∞). (21)

Как и в начале доказательства теоремы из § 6, из полной управля-

емости и наблюдаемости пар (A, b) и (A, c), соответственно, по лемме

3, примененной к системе

˙x = (Q + µbc

∗

)x, x ∈ R

(µ 6= 0),

207

где µ = s

− σ

, Q = A + σ

∗

, следует полная наблюдаемость

пары (A + σ

∗

, h). Аналогично, из леммы 2 § 6 следует, что пара

(A + σ

∗

, d), где d ∈ M

, d 6= 0 полностью управляема. Отсюда, ис-

пользуя лемму 3 из § 5, выводим, что функция h

∗

z(t, d), меняет свой

знак при некотором значении t, где

z(t; d) = e

— решение системы

˙z = Qz, z ∈ R

(Q = A + σ

∗

). (22)

В силу соотношения (21) при достаточно большом |µ

| существует

число τ

(µ

; d) > 0 такое, что

z(τ

(µ

; d); d) ∈ Ω(µ

Далее, двигаясь по многообразию Ω(µ

) вдоль траектории

ϕ(t; x

, µ

), x

∈ L

, системы (1) с µ = µ

(если ϕ(t; x

, µ

) при-

ближается к L

при возрастании t) или системы (1) с µ = −µ

(если

ϕ(t; x

, µ

) удаляется от L

при возрастании t) достигнем в некото-

рый момент

t = τ > max{τ

(µ

; d), τ

(−µ

, d)}

множества L

. Здесь τ

(−µ

; d) — время достижения траекторией си-

стемы (20) интегрального многообразия Ω(−µ

) системы (1) с

µ = −µ

(рис. 21)

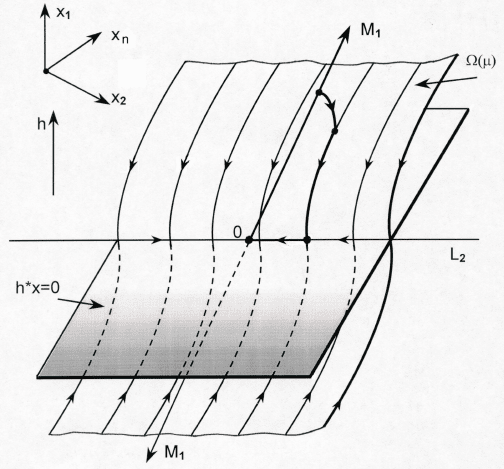
208

Рис.21. Отображение неустойчивого многообразия M

в устойчивое L

Заметим, что в силу автономности рассматриваемых систем за

счет выбора движений вдоль траекторий, образующих многообразия

Ω(µ

) и Ω(−µ

), можно добиться того, чтобы время τ достижения

множества L

было одним и тем же для всех точек d ∈ M

Отметим также, что многообразия Ω(µ

) и Ω(−µ

) достаточно

близки друг к другу, но направления движений на траекториях, со-

ставляющих эти многообразия, различные (это следует из того, что

решения систем ˙x = (A/µ

+ bc

∗

)x и ˙x = (−A/µ

+ bc

∗

)x при доста-

точно большом |µ

| сколько угодно близки к решениям системы (20)

по теореме о непрерывной зависимости решения от параметра).

Таким образом, отображение неустойчивого подпространства M

(прямой) в устойчивое L

(размерности n −2) происходит в два эта-

па. Сначала под действием фазового потока {f

} системы (22) точки

множества M

, двигаясь вдоль траекторий потока {f

} в течение

времени τ

= τ

(µ

, d) (зависящим от µ

и точки d ∈ M

), попадают

209

на интегральное многообразие Ω(µ

) системы (1) с µ = µ

или ин-

тегральное многообразие Ω(−µ

) системы (1) с µ = −µ

, а затем на

интервале времени (τ

, τ ), двигаясь под действием фазового потока

} системы (1) с µ = µ

(или µ = −µ

) вдоль траекторий этого по-

тока (вдоль многообразия Ω(µ

) или Ω(−µ

)), достигают множества

в момент t = τ , т.е.

⊂ L

Следовательно, выполняется "условие вложения многообразий"(6)

из § 4 (здесь θ

:= g

Итак, выполнены все условия основной теоремы (§ 4) и, поэтому,

система (12) асимптотически устойчива. Теорема 4 доказана.

§ 8. Необходимые условия стабилизации

В предыдущих параграфах были даны достаточные условия ста-

билизируемости рассматриваемых систем. Здесь мы приведем необ-

ходимые условия стабилизируемости системы

˙x = Ax + bu, y = c

∗

x (x ∈ R

) (1)

(где A — постоянная (n×n)-матрица, b, c ∈ R

) со скалярным входом

u ∈ R и скалярным выходом y ∈ R.

Предположим, что передаточная функция

W (p) = c

∗

(A − pI)

−1

системы (1) невырождена. Тогда ее можно представить в виде отно-

шения

W (p) =

ν(p)

∆(p)

двух многочленов

ν(p) = c

n−1

+ c

n−1

n−2

+ ··· + c

, c

∈ R,

∆(p) = p

+ a

n−1

+ ··· + a

, a

∈ R (k = 1, . . . , n),

не имеющих общих нулей (здесь ∆(p) — характеристический много-

член матрицы A).

Имеет место следующая теорема, дающая достаточные условия

невозможности стабилизации системы (1).

210

Теорема 1. Предположим, что для системы (1) выполнены сле-

дующие условия:

1) при n > 2 c

≤ 0, . . . , c

n−1

≤ 0 (при n = 2 c

≤ 0),

2) c

− c

n−1

) > a

+ c

− c

n−1

) > a

. . . . . . . . .

n−2

+ c

n−1

− c

n−1

) > a

n−1

Тогда не существует функции s(t), для которой система

˙x = (A + s(t)bc

∗

)x (x ∈ R

) (2)

асимптотически устойчива.

Д о к а з а т е л ь с т в о . В силу следствия теоремы 2 из § 3,

гл.II систему (2) можно привести к виду











˙x

= x

˙x

n−1

= x

˙x

= −(a

+ ··· + a

) − s(t)(x

+ c

n−1

+ ··· + c

(3)

Рассмотрим множество

Ω = {x ∈ R

: x

≥ 0, . . . , x

n−1

≥ 0, x

+ c

n−1

+ ··· + c

≥ 0}.

Докажем, что Ω положительно инвариантно относительно решений

системы (3), т.е. если для решения x(t; x

, t

), (x(t

; x

, t

) = x

) си-

стемы (3) выполнено включение x

∈ Ω, то x(t; x

, t

) ∈ Ω для всех

t ≥ t

(рис.22).