Леонов Г.А., Шумафов М.М. Проблемы стабилизации линейных управляемых систем

Подождите немного. Документ загружается.

171

В силу предложения 1 (из § 2) матрицами преобразований f

за время t являются нормированные фундаментальные матрицы

(t) и Ψ

(t) решений систем (6) и (7) соответственно.

Ясно, что существует число T

> 0 такое, что линейный оператор

(описываемый матрицей Ψ

) ) преобразует прямую x

= `

в прямую x

= `

Из равенства ν = 1 следует, что прямую x

= `

в прямую

= `

переводят также операторы

+2πj

, j ∈ Z.

Покажем теперь, что в качестве числа T можно выбрать значение

2(T

+ 2πj) с достаточно большим j. Для этого рассмотрим единич-

ный круг

= {x

+ x

≤ 1}.

Докажем, что оператор монодромии H = h

= f

3T/4

T/4

си-

стемы (4) переводит круг E

в эллипс, лежащий в круге

1/2

= {x

+ x

≤

}

радиуса 1/2, т.е. что точки круга E

, двигаясь под действием фазово-

го потока {f

} системы (4) вдоль его траекторий попадут при t = T

в круг E

1/2

(заметим, что согласно предложению 4 из § 2 H = h

—

линейный оператор.)

Так как на промежутке [0, T/4) мы имеем фазовый поток {f

} си-

стемы (6), действующий как сжатие в e

−`

раз в направлении пря-

мой x

= `

и одновременно как растяжение в e

раз в направ-

лении прямой x

= `

, то преобразование g

T/4

за время от t = 0

до t = T/4 переведет круг E

в эллипс, лежащий в ε-окрестности U

прямой x

= `

, где

ε = µ

T/4

причем

(T/4)

+ x

(T/4)

≤ µ

T/2

(8)

(здесь µ

> 0 и µ

> 0 — некоторые числа; за счет выбора µ

можно

считать µ

< µ

). Поэтому образ круга E

при преобразовании f

T/4

(за время t = T/4 ) будет лежать в пересечении ε-окрестности U

круга K

радиуса µ

T/4

с центром в начале координат.

172

На промежутке времени [T/4, 3T/4) действует фазовый поток {g

}

системы (7). Поэтому в результате действия (линейного) оператора

3T/4

T/4

(= g

T/2

в силу автономности системы (7)) область U

перехо-

дит в µ

ε-окрестность U

прямой x

= `

(здесь µ

> 0 — неко-

торое число). При этом из соотношения (8) следует, что (считаем

< µ

)

(3T/4)

+ x

(3T/4)

≤ µ

T/2

, (9)

(так как h

T/2

есть сжатие с одновременным вращением).

Таким образом, в результате преобразования g

3T/4

T/4

образ круга

будет лежать в пересечении области U

с кругом K

На промежутке [3T/4, T ) снова действует фазовый поток {f

} си-

стемы (6). Поэтому в результате действия оператора f

3T/4

(= f

T/4

силу автономности системы (6)) область U

переходит в ε

-окрест-

ность U

прямой x

= `

, где

= µ

ε · µ

T/4

= µ

)T/4

причем с учетом (9)

(T )

+ x

(T )

≤ µ

)T/4

(здесь µ

и µ

— некоторые положительные числа; за счет выбора µ

и µ

считаем выполненным неравенство µ

< µ

Следовательно, образ Hx любой точки x = (x

, x

)

∗

∈ E

при

отображении H (с помощью траекторий системы (4)) за время от

t = 0 до t = T :

Hx = f

T/4

T/2

T/4

лежит в пересечении окрестности U

и круга K

радиуса

)T/4

( с центром в начале координат).

Так как `

= −α < 0, то выбирая число T достаточно большим,

можно добиться выполнения неравенства

)T/4

< 1/2,

т.е.K

будет кругом радиуса r = 1/2 : K

= E

1/2

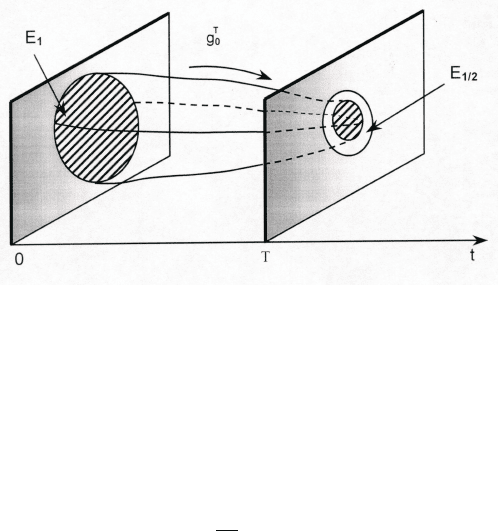
Итак, оператор монодромии H (преобразование за время T ) пе-

реводит круг E

в эллипс, лежащий в E

1/2

(рис.15):

⊂ E

1/2

173

Рис.15. Оператор монодромии системы (4), (5).

Из последнего соотношения и линейности оператора H следует,

что H есть сжимающий оператор в E

(и, следовательно, в R

), т.е.

|Hz| < q|z| ∀z ∈ E

, (10)

где q = 1/2, z = (x

, x

)

∗

. Поэтому из (10) получаем

z| <

|z| ∀z ∈ E

. (11)

Отсюда

z| → 0 при ∀z ∈ E

. (12)

Из соотношений (11) и (12) вытекает асимптотическая устойчи-

вость отображения H и, следовательно, в силу леммы 2 из § 2 асимп-

тотическая устойчивость системы (4) с функцией вида (5). Теорема

полностью доказана.

Замечание. Таким образом, описанный в доказательстве преды-

дущей теоремы алгоритм стабилизации системы (4) весьма прост.

Во-первых, с помощью фазового потока {f

} системы (6) соверша-

ется сжатие фазового пространства R

в направлении устойчивого

многообразия `

системы (6) и растяжение в направлении её неустой-

чивого многообразия `

, при этом сжатие происходит быстрее, чем

растяжение. Во-вторых, это неустойчивое многообразие `

, после пе-

реключения с траекторий системы (6) на траектории системы (7),

под действием фазового потока {g

} системы (7) можно повернуть

174

вдоль ее траекторий так, чтобы достичь к следующему переключе-

нию (с траекторий системы (7) обратно на траектории системы (6))

его совпадения с устойчивым многообразием `

. В-третьих, дей-

ствуя снова фазовым потоком {f

} системы (6) мы осуществляем

превалирование сжатия над растяжением и в целом к моменту вре-

мени t = T полностью ликвидируем растяжение, погружая траекто-

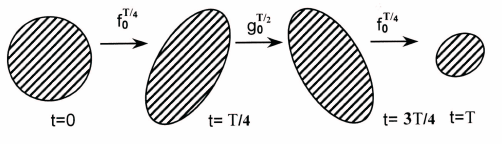
рии в шар сколь угодно малого радиуса (рис.16).

Рис.16. Действие оператора монодромии (преобразования за время T )

системы (4), (5).

§ 4. Проблема Брокетта в классе кусочно-постоянных

периодических матриц

Рассмотрим теперь проблему Брокетта, сформулированную в § 1.

При ее решении мы будем использовать идеи предыдущего парагра-

фа.

1. Основная теорема. Предположим, что существуют (веще-

ственные) постоянные матрицы s

и s

такие, что линейные системы

˙x = (A + b(cs

)

∗

)x, x ∈ R

(j = 1, 2) (1)

(где A, b и c — вещественные постоянные матрицы) обладают устой-

чивыми инвариантными (линейными) многообразиями L

и инвари-

антными (линейными) многообразиями M

. Пусть

∩ L

= {O}, dim L

+ dim M

= n (2)

(знак dim в (2) означает размерность соответствующего простран-

ства) и для положительных чисел λ

, κ

, α

, β

выполнены неравен-

ства

(t; x

)| ≤ α

−λ

∀x

∈ L

, (3)

(t; x

)| ≤ β

∀x

∈ M

. (4)

175

Здесь x

(t; x

) — решение системы (1) с начальным условием

(0; x

) = x

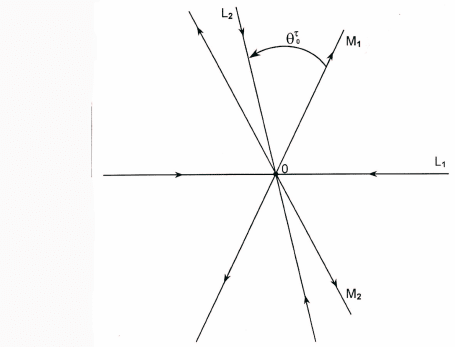
Рис.17. Линейные устойчивые L

и неустойчивые M

многообразия

(j = 1 , 2); θ

⊂ L

Предположим, далее, существование непрерывной матрицы σ(t) и

числа τ > 0 таких, что фазовый поток {θ

} системы

˙x = (A + b(cσ(t))

∗

)x, x ∈ R

, (5)

(где A, b и c — вещественные постоянные матрицы) за время от t = 0

до t = τ переводит многообразие M

в многообразие, лежащее в L

т.е.

⊂ L

. (6)

Будем называть условие (6) ниже "условием вложения многооб-

разий" (рис. 17).

При этих предположениях имеет место следующая

Теорема 1. (Основная теорема.) Пусть выполнено неравен-

ство

> κ

. (7)

Тогда существует периодическая матрица s(t) такая, что система

˙x = (A + b(cs(t))

∗

)x (x ∈ R

) (8)

176

является асимптотически устойчивой.

Д о к а з а т е л ь с т в о . Из условия (7) следует, что для любого

T > 0 существуют положительные числа t

и t

, удовлетворяющие

неравенствам

−λ

+ κ

< −T,

−λ

+ κ

< −T.

Определим теперь периодическую матрицу s(t) следующим обра-

зом:

s(t) =







при t ∈ [0, t

σ(t − t

) при t ∈ [t

, t

+ τ),

при t ∈ [t

+ τ, t

+ t

+ τ),

s(t + T ) = s(t),

(9)

где T = t

+ t

+ τ.

Покажем, что при достаточно больших значениях T система (8)

с матрицей s(t), определенной согласно (9), будет асимптотически

устойчивой.

Для этого рассмотрим (как и в § 3) единичный шар E

= {x ∈

: kxk ≤ 1} и докажем, что фазовый поток {h

} системы (8) с

матрицей s(t) вида (9) переводит E

за время от t = 0 до t = T в

эллипсоид, лежащий в шаре E

1/2

= {x ∈ R

: kxk ≤ 1/2}, т.е.

⊂ E

1/2

где H = h

— оператор монодромии (преобразование за период T ).

Пусть {f

} – фазовый поток системы (1) с j = 1, а {g

} — фазовый

поток системы (1) с j = 2. Тогда

= g

+τ

, (10)

где ϑ

+τ

— преобразование за время от t

до t

+ τ , осуществляемое

фазовым потоком {ϑ

} системы

˙x = [A + b(cσ(t − t

))

∗

]x. (11)

Легко видеть, что в (10)

+τ

= θ

. (12)

(Последнее соотношение следует из того, что если x = ψ(t; x

, 0)

— решение системы (5) с начальным условием ψ(0; x

, 0) = x

, то

177

функция x = ϕ(t; x

, t

), где

ϕ(t; x

, t

) = ψ(t − t

; x

, t

есть решение системы (11) с начальным условием ϕ(t

; x

, t

) = x

Поскольку

x = e

[A+b(cs

)

∗

∈ R

, j = 1, 2))

— решение системы (1), а решение системы (5) есть

x = Ψ(t)x

∈ R

), (13)

где Ψ(t) — фундаментальная матрица решений системы (5), норми-

рованная при t = 0 (Ψ(0) = I), то (см. п.3, § 2)

= e

[A+b(cs

)

∗

, g

= e

[A+b(cs

)

∗

, θ

= Ψ(τ).

Пусть x

∈ E

— произвольная точка из шара E

. Тогда точка x

под действием потока {f

} (двигаясь вдоль траектории системы (1)

с j = 1 ) перейдет за время от t = 0 до t = t

в точку x

= f

— значение в момент t

решения x = ψ

(t; x

) системы (1), где

j = 1, с начальным условием ψ(0, x

) = x

). Затем, точка x

под дей-

ствием фазового потока {ϑ

} (двигаясь вдоль траектории системы

(11)) перейдет за время от t = t

до t = t

+ τ в точку x

= ϑ

+τ

— значение в момент t = t

+ τ решения x = ϕ(t; x

, t

) системы

(11) с начальным условием ϕ(t

; x

, t

) = x

. И, наконец, точка x

под действием потока {g

} (двигаясь вдоль траектории системы (1)

с j = 2) перейдет за время от t = t

+ τ до t = t

+ t

+ τ в точку

= g

+τ

— значение решения x = ψ

(t; x

) системы (1),

где j = 2, с начальным условием ψ

(0; x

) = x

Таким образом, с учетом (12), будем иметь

= h

= g

+τ

= g

(14)

+τ

= g

в силу автономности системы (1) (j = 2): если ψ

(t)

— решение, то и ψ

(t + C) — тоже решение, где C = const ).

Приведем систему (1) с помощью невырожденного линейного пре-

образования переменных

= B

x, ξ

∈ R

, η

∈ R

(j = 1, 2), (15)

178

где n

= dim L

, n

= dim M

, B

(j = 1, 2) — неособая матрица

(порядка n × n), к следующему виду

= P

˙η

= Q

(j = 1, 2).

Не умаляя общности, можно считать, что

|ξ

(t)| ≤ α

|ξ

(0)|e

−λ

|η

(t)| ≤ β

|η

(0)|e

(j = 1, 2). (16)

Так как в силу (13)

x(t

+ τ) = x

= Ψ(τ)x

где x

= x(t

), то с учетом (15) имеем

+ τ)

= B

Ψ(τ)B

−1

)

В силу "условия вложения многообразий"(6) для любого x

∈ M

Ψ(τ)x

= x

, x

∈ L

Поэтому (см. (15)),

−1

= Ψ(τ)B

−1

или

= B

Ψ(τ)B

−1

где

, B

Следовательно, матрица B

Ψ(τ)B

−1

имеет следующую структуру:

Ψ(τ)B

−1

(τ) b

(τ)

(τ) 0

|{z}

где b

(τ), b

(τ) — некоторые матрицы порядков (n

× n

) и (n

× n

) соответственно.

179

Очевидно, что матрицами преобразований f

и g

в новых пере-

менных (ξ

, η

) и (ξ

, η

) будут

−1

0 e

, B

−1

0 e

Поэтому в новых переменных соотношение (14) перепишется так:

(T )

0 e

¶µ

0 e

¶µ

(0)

Отсюда

(T ) = e

(0) + e

(0),

(T ) = e

(0).

Используя оценки (16), получим

kξ

(T )k ≤ α

k · kξ

(0)ke

−λ

+α

k · kη

(0)ke

−λ

+κ

(17)

kη

(T )k ≤ α

k · kη

(0)ke

−λ

+κ

. (18)

В силу выбора чисел t

> 0 и t

> 0 (см. начало доказательства)

из (17) и (18) имеем

kξ

(T )k ≤ C

−T

kη

(T )k ≤ C

−T

где C

и C

— некоторые положительные константы.

Из последних оценок следует, что при достаточно большом T > 0

(T )

k <

−1

Поэтому,

kx(T )k = kx

k = kB

−1

(T )

k <

Итак,

kHx

k <

∀x

∈ E

т.е. HE

⊂ E

1/2

Дальше, повторяя заключительную часть доказательства теоремы

из § 3, приходим, что система (8) с функцией s(t) вида (9), где T

— достаточно большое число, асимптотически устойчива. Теорема

доказана полностью.

180

Замечание. Идея доказательства теоремы 1 (как и теоремы из

§ 3) состоит в том, что сначала с помощью траекторий системы (1)

(j = 1) производится сжатие и растяжение единичного шара E

со-

ответственно вдоль многообразий L

и M

(преобразование f

причем сжатие происходит быстрее, чем растяжение; затем пере-

ключаясь на траектории системы (11), производится вращение про-

странства так, чтобы образ M

лежал в устойчивом многообразии

(преобразование θ

). Наконец, с помощью траекторий системы

(1) (j = 2) производится сжатие и растяжение вдоль многообразий

и M

соответственно, с превалированием сжатия над растяжени-

ем (преобразование g

). В результате таких преобразований образ

шара E

к моменту времени t = T будет лежать в шаре сколь угодно

малого радиуса (при соответствующем выборе T ).

2. Случай скалярной функции s(t). Рассмотрим теперь слу-

чай, когда матрица s(t) в уравнении (8) является скалярной функ-

цией и имеет вид (9):

σ(t) ≡ σ

, s

= s

, σ

∈ R, s

∈ R.

Предположим, что

< 0, λ

= λ

= λ, κ

= κ

= κ,

функция kθ

k ограничена на промежутке [0, +∞) и существует по-

следовательность {τ

} → +∞, для которой

⊂ L

. (19)

(Здесь {θ

} — фазовый поток системы (5): σ(t) ≡ σ

= e

[A+b(cσ

)

∗

Тогда справедлива

Теорема 2. Если выполнено неравенство

λ > κ

то существует T –периодическая функция s(t) с нулевым средним

на периоде такая, что система (8) является асимптотически устой-

чивой.