Леонов Г.А., Шумафов М.М. Проблемы стабилизации линейных управляемых систем

Подождите немного. Документ загружается.

161

Следующая теорема устанавливает критерий асимптотической ус-

тойчивости неподвижной точки x = 0 произвольного (не обязательно

H) линейного отображения.

Теорема 4 (Критерий асимптотической устойчивости ли-

нейного отображения .) Для асимптотической устойчивости

неподвижной точки x = 0 произвольного линейного отображения

F : R

→ R

необходимо и достаточно, чтобы все его собственные

значения ρ

лежали внутри единичного круга |p| < 1 (p ∈ C).

Д о к а з а т е л ь с т в о . Пусть Φ — матрица линейного отобра-

жения F в базисе {e

}

i=1

1. Дадим сначала оценку нормы матрицы Φ

, k ∈ N. Пусть

, ··· , ρ

— собственные числа матрицы Φ с учетом их кратностей.

Приведем матрицу Ψ к жордановой нормальной форме

J = SΦS

−1

= diag [J

(ρ

), ··· , J

(ρ

)] (m ≤ n), (24)

где

(ρ

) =







1 0 ··· 0

0 ρ

1 ··· 0

0 0 0

0 0 0 ··· ρ







(j = 1, ··· , m) (25)

— клетки Жордана порядков `

; ρ

, ··· , ρ

— собственные числа мат-

рицы Φ, соответствующие различным клеткам Жордана (не обяза-

тельно различные между собой), S — некоторая неособая матрица.

Из (24) имеем

= (S

−1

JS)

= S

−1

S, k ∈ N. (26)

Используя правило умножения клеточно-диагональных матриц,

найдем

= diag [J

(ρ

)

, ··· , J

(ρ

)

] (k ∈ N). (27)

162

Для матрицы (25) нетрудно подсчитать, что

(ρ

)







k·ρ

k−1

k(k−1)ρ

k−2

···

k(k−1)···(k−`

+2)ρ

k−`

−1)!

0 ρ

kρ

k−1

···

k(k−1)···(k−`

+3)ρ

k−`

−2)!

···

0 0 0 ··· ρ







(28)

Из (26)-(28) получаем

kΦ

k ≤ kS

−1

k · kJ

k · kSk ≤ C

max

(ρ

)

k ≤ C

max

|ρ

P (k),

(29)

где P (k) — некоторый многочлен от k степени r = max

− 1) с

положительными коэффициентами, а C

и C

— некоторые положи-

тельные константы.

Поскольку при любом µ > 1

lim

k→+∞

−k

P (k) = 0,

то из (29) имеем следующую оценку

kΦ

k ≤ C

(µγ)

(µ > 1), (30)

где γ = max

|ρ

|, C

— некоторая константа, зависящая от µ.

Если собственным числам матрицы Φ, имеющим максимальный

модуль соответствуют простые жордановые клетки (т.е. последние

сводятся к одному элементу), то в (29) P(k) = const и, поэтому,

вместо (30) будем иметь

kΦ

k ≤ Cγ

2. Докажем теперь утверждение теоремы 4. Пусть x ∈ R

. Тогда

образами этой точки при последовательном применении отображе-

ния F = Φ (здесь мы отождествляем отображение F с матрицей Φ )

будут точки

= Φ

x, k = 1, 2, ··· . (31)

163

Пусть собственные числа ρ

матрицы Φ расположены внутри еди-

ничного круга |p| < 1. Тогда, поскольку в (30) µ > 1 — произвольное

число, то всегда можно выбрать µ таким, чтобы µγ < 1.

Используя (30), оценим норму вектора x

из (31):

k ≤ kΦ

k · kxk ≤ C

(µγ)

kxk (k ∈ N). (32)

Так как µγ < 1, то, как легко видеть, из неравенства (32) следует

асимптотическая устойчивость неподвижной точки x = 0 отображе-

ния F , т.е. достаточность утверждения теоремы 4.

Докажем необходимость. Пусть неподвижная точка x = 0 отоб-

ражения F асимптотически устойчива. Допустим, что существует

собственное значение ρ

такое, что |ρ

| ≥ 1. Тогда, положив в (31)

x = ξ, где ξ — собственный вектор матрицы Φ, соответствующий её

собственному числу ρ

, будем иметь из (31)

= Φ

ξ = ρ

ξ (k ∈ N), (33)

поскольку Φξ = ρ

ξ. Из (33) получаем

kξ

k = |ρ

kξk ≥ kξk (∀k ∈ N).

Последнее неравенство означает отсутствие асимптотической устой-

чивости неподвижной точки x = 0 отображения F . Полученное про-

тиворечие доказывает необходимость утверждения теоремы 4.

Теорема 4 доказана.

О п р е д е л е н и е 6. Собственные значения ρ

(j = 1, . . . , n) оператора монодромии H (или соответствующей ей

матрицы монодромии Ψ(T )) называются м у л ь т и п л и к а т о р а-

м и с и с т е м ы (1).

Из теоремы 2

и 4 вытекает

Теорема 5. Линейная периодическая система (1) асимптотиче-

ски устойчива тогда и только тогда, когда все её мультипликато-

ры расположены внутри единичного круга |p| < 1 (p ∈ C).

Докажем теперь следующую теорему, которая устанавливает до-

статочные условия устойчивости по Ляпунову отображения

F : R

→ R

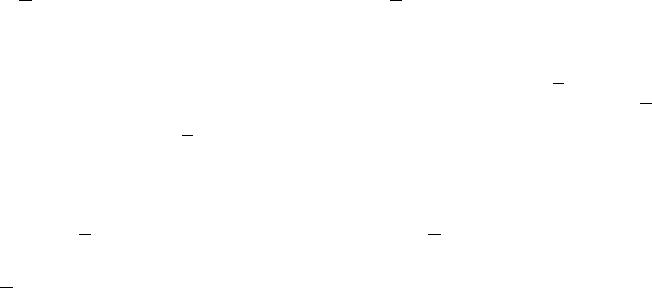
164

О п р е д е л е н и е 7. Линейное отображение F плоско-

сти R

на себя называется г и п е р б о л и ч е с к и м, если его соб-

ственные числа λ

и λ

вещественны, различны и λ

= 1, и

э л л и п т и ч е с к и м, если его собственные числа λ

и λ

комплекс-

но сопряжены и λ

= 1.

Лемма. Пусть F — линейное отображение плоскости на себя.

Тогда начало координат плоскости (x

, x

) устойчиво для эллипти-

ческого и неустойчиво для гиперболического отображений.

Короче: эллиптическое отображение — устойчивое отображе-

ние, а гиперболическое отображение — неустойчивое.

Д о к а з а т е л ь с т в о . Пусть F — эллиптическое отображение

и λ, λ — его собственные числа, причем λλ = 1. Собственному числу

λ отвечает собственный вектор z ∈ C

= CR

комплексифицирован-

ного оператора

F : C

→ C

(см. § 2, гл.I). Представим z в виде:

z = x + iy, x ∈ R

, y ∈ R

. Тогда сопряженный вектор z = x − iy

также является собственным вектором с собственным значением λ.

Так как векторы z и z линейно независимы в C

, то легко видеть, что

и векторы x, y будут линейно независимыми в R

, т.е. x и y образуют

базис в R

Найдем матрицу оператора

F в (вещественном) базисе x, y. По-

скольку λλ = 1, то собственные числа λ и λ лежат на единичной

окружности |p| = 1 плоскости комплексного переменного p. Поэтому

λ, λ = cos α ± i sin α, где α = arg λ. По определению

F имеем:

F x + i

F y =

F (x + iy) =

(cos α + i sin α)(x + iy) = (x cos α − y sin α) + i(x sin α + y cos α).

Отсюда

F x = x cos α − y sin α,

F y = x sin α + y cos α.

Поэтому матрицей оператора F : R

→ R

в базисе {x, y} будет

cos α sin α

−sin α cos α

Таким образом, отображение F аффинно эквивалентно повороту на

угол α и, следовательно, будет устойчивым, так как траектория про-

извольной точки ξ ∈ R

− {F

ξ, k ∈ N} — лежит на эллипсе.

165

Пусть теперь F — гиперболическое отображение. Тогда одно из

собственных чисел (пусть это λ

) меньше, а другое (λ

) больше 1

по модулю. Поэтому отображение F состоит из сжатия в |λ

−1

раз

в направлении собственного вектора ξ

, соответствующего собствен-

ному числу λ

, и растяжения в |λ

| раз в направлении собственного

вектора ξ

, соответствующего собственному числу λ

. Оператор F в

базисе {ξ

, ξ

} имеет матрицу

0 λ

Следовательно, отображение F аффинно эквивалентно гиперболи-

ческому повороту: (x

, x

) → (λ

; λ

) и, поэтому, неустойчиво,

так как траектории — {F

ξ, k ∈ N, ξ ∈ R

} — лежат на гиперболах

(траектория, начинающаяся в сколь угодно малой окрестности нача-

ла координат, после достаточно большого числа итераций F

выйдет

из любой фиксированной окрестности начала). Лемма доказана.

Теорема 6. Пусть Φ — матрица линейного отображения F плос-

кости на себя, причем det Φ = 1 (такое отображение сохраняет

площади).

Тогда начало координат устойчиво для отображения F (или, ко-

роче, отображение F устойчиво), если

|Tr Φ| < 2,

и неустойчиво, если

|Tr Φ| > 2.

Д о к а з а т е л ь с т в о . Характеристический многочлен матрицы

Φ имеет вид:

− σ · p + ∆,

где σ и ∆ — вещественные числа. Корни λ

и λ

этого многочлена

(собственные числа матрицы Φ) вещественны при |σ| > 2 и комплек-

сно-сопряжены при |σ| < 2. Так как

σ = λ

+ λ

= Tr Φ, ∆ = λ

= det Ψ = 1,

то в первом случае (|T r Φ| > 2) одно из собственных чисел по мо-

дулю больше, а другое меньше 1, а во втором случае (|T r Φ| < 2)

собственные числа λ

и λ

лежат на единичной окружности

166

|p| = 1. В первом случае, отображение F гиперболическое и, следо-

вательно, в силу доказанной выше леммы, неустойчиво, а во втором

случае, отображение F эллиптическое и, поэтому, в силу той же лем-

мы, устойчиво. Теорема 5 доказана.

Замечание. Как мы видели выше, при последовательном приме-

нении (итерациях) отображения монодромии H к произвольной точ-

ке x

∈ R

получаем последовательность {x

} точек x

∈ R

(k =

0, 1, 2, ···), причем

k+1

= Hx

(k = 0, 1, 2, ···). (34)

Последнее соотношение представляет собой дискретную систему.

Таким образом, здесь при рассмотрении определенных свойств ре-

шений (как, например, устойчивость) мы заменяем систему диффе-

ренциальных уравнений (1) на соответствующую ей линейную дис-

кретную систему (34), где H — отображение за время периода T ,

порождаемое траекториями системы (1).

Некоторые аспекты теории линейных дискретных систем будут

рассмотрены в гл.VI.

§ 3. Низкочастотная стабилизация верхнего положения

равновесия маятника

Прежде чем перейти к проблеме Брокетта и к алгоритмам постро-

ения соответствующих стабилизирующих функций s(t) для системы

(3) § 1, мы рассмотрим сначала классическую задачу о стабилиза-

ции верхнего положения равновесия маятника с вибрирующей точ-

кой подвеса.

Рассмотрим колебания маятника, который может свободно вра-

щаться в определенной вертикальной плоскости вокруг своей точки

подвеса. Предположим, что точка подвеса совершает в вертикальном

направлении колебания с некоторой амплитудой и частотой.

Спрашивается, может ли верхнее, обычно неустойчивое, поло-

жение равновесия маятника стать устойчивым ?

Как показано в работах [31,77] неустойчивое верхнее положение

равновесия маятника может сделаться устойчивым при достаточно

быстрых колебаниях точки подвеса (когда точка подвеса совершает

167

в вертикальном направлении гармонические колебания y = a sin ωt

или y = a cos ωt с малой амплитудой a и высокой частотой ω). Этот

хорошо известный эффект высокочастотной стабилизации верхнего

положения равновесия мы рассмотрим позже в следующей главе V.

Здесь же мы рассмотрим возможность стабилизации верхнего по-

ложения равновесия маятника при низкочастотных колебаниях точ-

ки подвеса.

Для рассмотрения этого интересного явления (стабилизации верх-

него положения равновесия) составим уравнение колебаний маятни-

ка с вибрирующей точкой подвеса.

Как хорошо известно, уравнение колебаний маятника с покоящей-

ся точкой подвеса имеет вид

θ + α

θ + ν

sin θ = 0 (ν

= g/`) (1)

(в предположении, что трение пропорционально скорости), где θ —

угол отклонения, отсчитываемый от нижнего положения равновесия,

α — коэффициент трения, ν

g/` — собственная частота малых

колебаний (` — длина маятника, g — ускорение свободного падения).

Пусть точка подвеса совершает колебания в вертикальном направ-

лении по закону y = y(t), где y(t) — некоторая периодическая функ-

ция. Чтобы составить уравнение колебаний маятника с вибрирующей

точкой подвеса воспользуемся принципом относительности, соглас-

но которому движение маятника с вертикально вибрирующей точкой

подвеса эквивалентно движению маятника с покоящейся точкой под-

веса, находящемуся в поле "силы тяжести"с ускорением g + y

(t).

Поэтому, заменяя в (1) g на g + y

(t), получим искомое уравнение

θ + α

θ +

g + y

(t)

sin θ = 0. (2)

Уравнение (2) допускает стационарное решение θ(t) ≡ π , соответ-

ствующее верхнему положению равновесия маятника (стационарное

решение θ(t) ≡ 0 соответствует нижнему положению равновесия ма-

ятника).

Для исследования устойчивости следует рассмотреть малые от-

клонения (вариации) δθ = θ − π от этого положения равновесия

(θ = π). Уравнение первого приближения (уравнение в вариациях)

168

выглядит так (переобозначив δθ → θ):

θ + α

θ + (s(t) − ν

)θ = 0, (3)

где s(t) = y

(t)/` (s(t) – с точностью до константы ускорение точ-

ки подвеса). Наиболее часто рассматриваются (мы их рассмотрим в

гл.V) функции s(t) вида s

+βω cos ωt (или s

+βω

cos ωt) ([259,260])

и периодические функции вида ([16,17])

s(t) =

β при t ∈ [0, T/2),

−β при t ∈ [T/2, T ),

s(t + T ) = s(t), t ∈ [0, +∞),

где β > 0 — некоторое число, а T — период функции s(t).

Исследуем уравнение (3). Задача состоит в том, чтобы найти функ-

цию s(t) такую, чтобы положение равновесия (θ = 0,

θ = 0) уравне-

ния (3) было асимптотически устойчивым (напомним, что в уравне-

нии (3) θ — угол отклонения, отсчитываемый от верхнего положения

равновесия).

Перейдем от уравнения (3) к эквивалентной ему системе

(

)

˙x

= x

˙x

= −αx

− (s(t) − ν

(4)

где стабилизирующая функция s(t) подлежит определению.

Будем искать стабилизирующую функцию s(t) в классе кусочно-

постоянных периодических с периодом T (где T — достаточно боль-

шое число) функций вида

s(t) =







−β при t ∈ [0, T/4),

β при t ∈ [T/4, 3T/4),

−β при t ∈ [3T/4, T ),

s(t + T ) = s(t) ∀T ∈ [0, +∞)

(5)

(где β > 0), имеющих нулевое среднее на периоде (см (4) § 1).

Для функций s(t) вида (5) покажем возможность стабилизации

верхнего положения равновесия маятника при низкочастотных ко-

лебаниях точки подвеса.

Имеет место следующая

Теорема. Пусть в системе (4), (5)

< 4(β − ν

169

Тогда для любого числа M > 0 существует число T > M такое, что

система (4) с функцией s(t) вида (5) асимптотически устойчива.

Д о к а з а т е л ь с т в о . Прежде всего, заметим, что, не умаляя

общности, можно считать

≡ β − ων

− α

/4 = 1.

Этого можно добиться всегда, сделав в уравнении (3) (или в системе

(4)) замену времени

τ = νt.

Рассмотрим нужные нам свойства системы (4), когда s(t) = −β и

s(t) = β.

При s(t) = −β система (4), т.е. система

˙x

= x

˙x

= −αx

+ (β + ν

(6)

имеет седловую особую точку (x

= 0, x

= 0) с неустойчивым мно-

гообразием M

= {x

= `

} и устойчивым многообразием

= {x

= `

} (рис.13).

Рис.13. Неустойчивое (верхнее) положение

равновесия уравнения маятника —седло.

170

Здесь

= −

+ (β + ν

) (`

= λ

> 0),

= −

−

+ (β + ν

) (`

= λ

< 0),

( `

и `

совпадают с корнями λ

и λ

характеристического уравнения

+ αp − (β + ν

) = 0).

Фазовый поток {f

} системы (6) состоит из сжатий в e

−`

раз в

направлении прямой x

= `

и одновременного растяжения в e

раз в направлении прямой x

= `

В силу условия α

< 4(β −ω

) теоремы характеристический мно-

гочлен p

+ αp + (β − ν

) = 0 системы (4) при s(t) = β, т.е. системы

˙x

= x

˙x

= −αx

− (β −ν

(7)

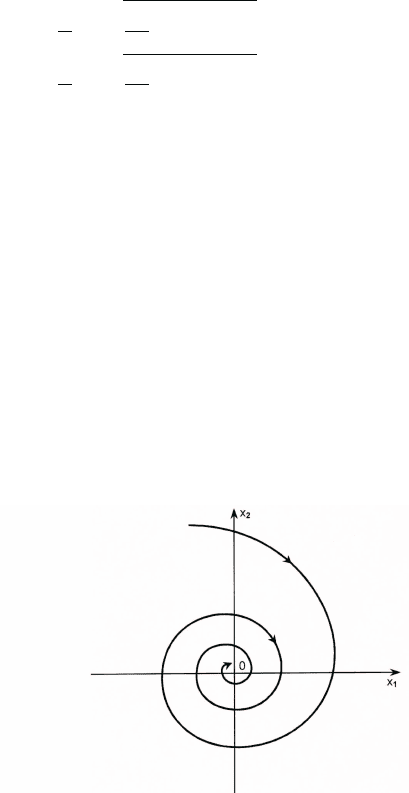
имеет комплексно-сопряженные корни −α/2 ± i (ν = 1) и, следова-

тельно, положение равновесия (0, 0) системы (7) — устойчивый фо-

кус (рис.14).

Рис.14. Положение равновесия системы (7) — устойчивый фокус.

Фазовый поток {g

} системы (7) аффинно эквивалентен семейству

сжатий в e

αt/2

раз с одновременным вращением на угол t.