Леонов Г.А., Шумафов М.М. Проблемы стабилизации линейных управляемых систем

Подождите немного. Документ загружается.

151

определено не всюду: при x = 1/t оно не определено. Причина со-

стоит в некомпактности пространства R. Но если компактифициро-

вать R, дополнив его бесконечно удаленной точкой ∞, и продолжить

поле v(x) = x

гладко с аффиной прямой R на полученную проек-

тивную прямую RP, то гладкое векторное поле v(x) = x

на RP

уже определяет фазовый поток. Это следует из следующего общего

утверждения [16]: всякое гладкое поле на компактном многообразии

(каковым является RP) определяет фазовый поток.

3. Основные свойства фазового потока. Сначала приведем

следующую основную теорему из теории линейных уравнений.

Теорема 1 ([16]). Множество всех решений {ψ} системы (1) яв-

ляется линейным пространством, изоморфным фазовому простран-

ству R

этой системы.

(Линейные пространства L

и L

называются изоморфными, если

между их элементами можно установить взаимно–однозначное соот-

ветствие, которое согласовано с операциями в L

и L

т.е. из

←→ x

, y

←→ y

, y

∈ L

; x

, y

∈ L

)

следует

+ y

←→ x

+ y

, cx

←→ cx

(c — произвольное число).)

Д о к а з а т е л ь с т в о т е о р е м ы 1. Первая часть утверждения

теоремы очевидна: если ψ

(t) и ψ

(t) — решения системы (1), то

(t) + c

(t)] = c

(t) + c

(t) =

= c

A(t)ψ

(t) + c

A(t)ψ

(t) = A(t)[c

(t) + c

(t)].

Для доказательства второй части теоремы определим отображе-

ние G

, сопоставляющее каждому решению ψ его значение в момент

t ∈ R:

: {ψ} → R

, G

ψ = ψ(t).

Очевидно, отображение G

линейно, так как

+ c

) = (c

+ c

)(t) =

= c

(t) + c

(t) = c

) + c

152

Образ отображения G

есть все фазовое пространство R

, посколь-

ку по теореме сущнствования для любого x

∈ R

существует реше-

ние ψ с начальным условием ψ(t

) = x

Далее, если решение ψ 6≡ 0, то значение G

ψ 6= 0, т.е. ядро (про-

образ нулевого элемента) линейного отображения G

состоит только

из нулевого решения ψ ≡ 0, так как по теореме единственности ре-

шений, из равенства G

ψ = 0 будет следовать ψ ≡ 0.

Таким образом, G

есть линейный изоморфизм линейного про-

странства решений {ψ} на фазовое пространство R

. Теорема 1 до-

казана.

Следствие 1. Размерность линейного пространства решений си-

стемы (1) равна n.

Следствие 2. Любая система (1) имеет n линейно независимых

решений (как элементов линейного пространства {ψ}) ψ

, ··· , ψ

ими являются любые решения, образующие базис линейного про-

странства {ψ}, а именно, решения ψ

(j = 1, ··· , n) системы (1),

удовлетворяющие начальным условиям, соответственно

) = ε

, ··· , ψ

) = ε

где {ε}

j=1

— произвольный базис в пространстве R

Система решений {ψ

}

j=1

, т.е. базис пространства решений {ψ},

называется фундаментальной системой решений, а матрица, столб-

цами которой являются координаты решений ψ

, называется фунда-

ментальной матрицей решений системы (1). Ясно, что эта матрица

при любом фиксированном t ∈ R невырождена (т.е. её определитель

отличен от нуля для любого t ∈ R).

Следствие 3. Преобразование g

: R

→ R

, соответствующее

системе (1), есть линейный изоморфизм, т.е. линейное обратимое

отображение фазового пространства R

на себя.

Д о к а з а т е л ь с т в о . Поскольку отображение G

, введен-

ное в доказательстве теоремы, является линейным изоморфизмом

пространства решений {ψ} на R

, то существует обратное отобра-

жение G

−1

: R → {ψ} (являющееся тоже линейным изоморфизмом)

сопоставляющее каждому вектору x

∈ R решение ψ системы (1) с

начальным условием ψ(t

) = x

153

Теперь преобразование g

можно, очевидно, представить как ком-

позицию (произведение) двух отображений G

−1

и G

, т.е.

= G

· G

−1

(∀t

, t ∈ R).

Отсюда следует утверждение следствия 3.

Перейдем теперь к свойствам преобразования g

. Из теоремы един-

ственности решений и формулы (3) сразу вытекает следующее о с н о-

в н о е с в о й с т в о п р е о б р а з о в а н и я g

· g

= g

(∀t

, t

, t ∈ R).

Предложение 1. Матрицей линейного преобразования (отобра-

жения) g

: R

→ R

(в фиксированном координатном базисе {e

}

i=1

пространства R

) является матрица

K(t, t

) = Ψ(t)Ψ

−1

), (6)

где Ψ(t) — фундаментальная матрица решений системы (1).

В частности, если матрица Ψ(t) нормирована при t = t

, т.е.

Ψ(t

) = I (где I — единичная матрица), то

K(t, t

) = Ψ(t). (7)

Таким образом, если отождествить линейное преобразование g

матрицей, представляющей его в базисе {e

}

i=1

, то

= K(t, t

). (8)

(Матрица K(t, t

) называется матрицей Коши.)

Д о к а з а т е л ь с т в о . Пусть Ψ(t) = (ψ

, ··· , ψ

) — любая фун-

даментальная матрица решений {ψ

}

j=1

системы (1), построенная в

силу следствия 2. Так как столбцы матрицы Ψ(t) образуют базис в

пространстве решений {ψ} системы (1), то любое решение ψ системы

(1) можно представить в виде

ψ(t) = Ψ(t)c, (9)

где c ∈ R

— некоторый постоянный вектор.

Пусть ψ(t

) = x

. Тогда, полагая в (9) t = t

, будем иметь

= Ψ(t

)c;

154

отсюда c = Ψ

−1

. Следовательно,

ψ(t) = Ψ(t)Ψ

−1

т.е.

ψ(t) = K(t, t

(10)

для любого решения ψ(t), удовлетворяющего начальному условию

ψ(t

) = x

(здесь K(t, t

) — матрица (6) или (7)).

Сравнивая равенство (10) с формулой (3), определяющей преоб-

разование g

, получаем (8). Предложение 1 доказано.

Замечание 1. В случае, когда (1) — система с постоянной мат-

рицей: A(t) ≡ A, решение ψ системы (1) с начальным условием

ψ(t

) = x

, как хорошо известно, имеет вид

ψ(t) = e

A(t−t

)

Отсюда и из равенства (9) (в силу теоремы единственности) полу-

чаем

K(t, t

) = e

A(t−t

)

т.е. в силу (8)

= e

A(t−t

)

. (11)

Из (4), (5) (см. замечание п.1) и равенства (11) следует, что для

линейной системы ˙x = Ax (x ∈ R) с постоянной матрицей A пре-

образование g

за время t равно e

, т.е.

= e

(∀t ∈ R).

Замечание 2. Во всех вышеприведенных рассуждениях относи-

тельно системы (1) нигде не использовался факт периодичности мат-

рицы-функции A(t). Поэтому все сделанные выше выводы (относи-

тельно системы (1)) справедливы также и для систем с любой (не

обязательно периодической) кусочно-непрерывной матрицей A(t).

В следующем утверждении существенно будет использоваться ус-

ловие периодичности матрицы-функции A(t) в системе (1).

Предложение 2. Преобразование g

за время от t

до t

не ме-

няется при одновременном увеличении t

и t

на величину периода

155

T матричной функции A(t) в системе (1), т.е.

= g

. (12)

Д о к а з а т е л ь с т в о . В силу периодичности правой части

системы (1), сдвиг ϕ(t) = ψ(t + T ) любого решения ψ(t) на время T

(вдоль оси t в расширенном фазовом пространстве R

n+1

) будет снова

решением системы (1):

dϕ(t)

dψ(t + T )

d(t + T )

= A(t + T )ψ(t + T ) = A(t)ϕ(t).

Следовательно,

ψ(t

+ T ; x

, t

+ T ) = ψ(t

; x

, t

). (13)

(Здесь ψ(t; x

, t

) — решение системы (1) с начальным условием

ψ(t

; x

, t

) = x

Из равенств (13) и (3) следует соотношение (12). Предложение 2

доказано.

4. Отображение за период. Пусть {g

} — фазовый поток си-

стемы (1). Рассмотрим преобразование g

:= 0, t := T ).

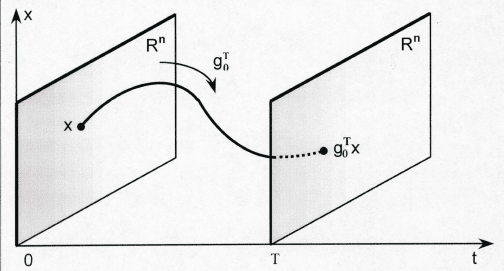
О п р е д е л е н и е 3. Преобразование g

, осуществляемое

фазовым потоком системы (1) за время одного периода T , назы-

вается о т о б р а ж е н и е м з а в р е м я T или о т о б р а ж е н и е м

(о п е р а т о р о м ) м о н о д р о м и и (рис.12).

Будем обозначать это отображение через H:

H = g

: R

→ R

156

Рис.12. Отображение монодромии.

Таким образом, g

x есть значение в момент t = T решения ψ(t; x)

системы (1) с начальным условием ψ(0; x) = x:

x = ψ(T ; x), x ∈ R

. (14)

Пример. Уравнения малых колебаний маятника

˙x

= x

˙x

= −x

;

˙x

= x

˙x

= x

(обычного и перевернутого соответственно) имеют вид (1) с

A(t) ≡ A

(k = 1, 2), где соответственно

0 1

−1 0

, A

0 1

1 0

Поэтому за период можно принять любое положительное число.

Матрица преобразования H за период T для уравнений обычного

маятника имеет вид (см. (14) и пример 6 из п.2: t := T )

H =

cos T sin T

−sin T cos T

Поэтому преобразование H (отображение монодромии) есть эллип-

тический поворот (на угол T ).

157

Для уравнений перевернутого маятника матрица преобразования

за период (см.(14) и пример 7 из п.2: t := T )

H =

ch T sh T

sh T ch T

Поэтому здесь отображение монодромии есть гиперболический по-

ворот (на угол T ).

Приведем некоторые общие свойства отображения монодромии H.

Предложение 3. Преобразование за время nT , где n ∈ N, явля-

ется n-й степенью отображения монодромии, т.е.

= H

. (15)

Кроме того, имеет место также соотношение

nT +τ

= g

. (16)

Д о к а з а т е л ь с т в о . В силу основного свойства преобразования

(см. п.3), где положено t

= 0, t := hT + τ , имеем

nT +τ

= g

nT +τ

· g

Из последнего соотношения, учитывая равенство g

nT +τ

= g

(см. предложение 2), получаем

nT +τ

= g

т.е. имеет место (16).

Соотношение (15) очевидно при n = 1. Пусть n = k. Положив в

(16) n := k и τ = T , будем иметь

(k+1)T

= g

· g

= Hg

(k ∈ N).

Отсюда по индукции (15) имеет место для любого n ∈ N. Предложе-

ние 3 доказано.

Замечание. В доказательствах предложений 2 и 3 нигде не ис-

пользуется факт линейности по x правой части уравнения (1). Поэто-

му предложения 2 и 3 справедливы для любого уравнения ˙x = f(t, x)

с периодически зависящей от времени t гладкой по x правой частью:

f(t + T, x) = f(t, x) (x ∈ R

158

Предложение 4. Отображение H = g

: R

→ R

есть линей-

ный изоморфизм, причем матрицей линейного отображения (опе-

ратора) H (в координатном базисе {e

}

i=1

пространства R

) явля-

ется матрица

K(T, 0) = Ψ(T )Ψ

−1

(0), (17)

где Ψ(t) — фундаментальная матрица решений системы (1).

В частности, если матрица Ψ(t) нормирована при t = 0 (т.е.

Ψ(0) = I), то

H ≡ g

= Ψ(T ) (18)

(если отождествить оператор H с её матрицей Ψ(T ) в базисе

}

i=1

( Матрица Ψ(T ) называется м а т р и ц е й м о н о д р о м и и .)

Д о к а з а т е л ь с т в о . Предложение 4 следует из следствия

3 доказанной в п.3 теоремы 1 и предложения 1 (формулы (17), (18)

следуют из (6) и (7), где положено t

= 0, t = T ).

5. Устойчивость отображения монодромии. Свойству устой-

чивости нулевого решения системы (1) соответствует аналогичное

свойство и для неподвижной точки x

= 0 (Hx

= x

) отображения

монодромии H.

О п р е д е л е н и е 4. Неподвижная точка x

отобра-

жения H : R

→ R

(Hx

= x

) называется у с т о й ч и в о й п о

Л я п у н о в у , если для любого ε > 0 существует δ > 0 такое, что

для любого x ∈ R

, удовлетворяющего условию |x − x

| < δ, выпол-

няется соотношение

x − H

| < ε (H

= x

)

для всех k ∈ N.

О п р е д е л е н и е 5. Неподвижная точка x

отображения

H называется асимптотически устойчивой, если она устойчива по

Ляпунову и еще выполняется дополнительное условие: для любой

точки x ∈ R

x − H

→ 0 (H

= x

)

при k → +∞.

159

Замечание. Определения 4 и 5 аналогичны соответствующим

определениям устойчивости по Ляпунову и асимптотической устой-

чивости тривиального решения для систем дифференциальных урав-

нений вида ˙x = f(t, x) (см. § 1, гл.III ).

Следующая теорема сводит вопрос об асимптотической устойчиво-

сти системы (1) к асимптотической устойчивости соответствующего

ей отображения монодромии H.

Теорема 2. Нулевое решение x(t) ≡ 0 системы (1) устойчиво

по Ляпунову (асимптотически устойчиво) тогда и только тогда,

когда неподвижная точка x

= 0 отображения монодромии H :

→ R

устойчива по Ляпунову (асимптотически устойчива).

Поскольку устойчивость (асимптотическая устойчивость) нулево-

го решения системы (1) равносильна устойчивости (асимптотической

устойчивости) всей системы (1) (см. § 1, гл.III ), то теорему 2 можно

переформулировать так.

Теорема 2

. Для устойчивости по Ляпунову (асимптотической

устойчивости) системы (1) необходимо и достаточно, чтобы непо-

движная точка x

= 0 отображения H была устойчивой по Ляпу-

нову (асимптотически устойчивой).

Д о к а з а т е л ь с т в о т е о р е м ы 2. Если решение

x(t) ≡ 0 асимптотически устойчиво, то, очевидно, и неподвижная

точка x

= 0 асимптотически устойчива.

Обратно, пусть неподвижная точка x

= 0 асимптотически устой-

чива. Из непрерывной зависимости решения ψ(t; y) системы (1) от

начальных условий на отрезке [0, T ] следует, что для любого ε > 0

существует такое числo

δ > 0, что для любого решения ψ(t; y) с на-

чальным условием ψ(0, y) = y : kyk <

δ выполнено неравенство

kψ(t; y)k < ε для всех t ∈ [0, T ], т.е. в силу (3)

yk < ε ∀t ∈ [0, T ]. (19)

В силу устойчивости по Ляпунову неподвижной точки x

= 0 по

числу

δ > 0 можно найти число δ > 0 такое, что для любой точки

x ∈ R

: |x| < δ справедливо соотношение:

xk <

δ ∀k ∈ N. (20)

= 0 ∀k ∈ N).

160

Пусть t ∈ [0, +∞) — произвольное число. Представим t в виде:

t = kT + τ, τ ∈ [0, T ). Используя формулы (16) и (15), имеем:

kψ(t; x)k = kg

xk = kg

x)k. (21)

Полагая y = H

x в (20),(21), получаем из (19) и (21):

|ψ(t; x)| < ε для всех t ∈ [0, +∞),

если только kxk < δ. Последнее означает, что нулевое решение

x(t) ≡ 0 системы (1) устойчиво по Ляпунову.

Аналогично доказывается и соотношение

lim

t→+∞

ψ(t; x) = 0 ∀x ∈ R

. (22)

Действительно, в силу того, что по условию

lim

k→+∞

x = 0

для любой начальной точки x ∈ R

, по заданному числу δ > 0 можно

найти такой номер K, что выполнено неравенство

xk < δ ∀ k ≥ K. (23)

Используя (23) и (19) (где y = H

x), из (21) получим

kψ(t; x)k < ε ∀ t ≥ KT (x ∈ R

что доказывает соотношение (22). Следовательно, нулевое решение

x(t) ≡ 0 уравнения (1) асимптотически устойчиво. Теорема 2 дока-

зана.

Замечание. Отображение H позволяет также обнаружить перио-

дические решения системы (1) и исследовать их устойчивость. Верно

следующее утверждение.

Теорема 3. Система (1) имеет периодическое решение ψ(t) с

начальным условием ψ(0) = x

тогда и только тогда, когда x

есть неподвижная точка отображения H. Это периодическое ре-

шение устойчиво по Ляпунову (асимптотически устойчиво) в том

и только в том случае, когда неподвижная точка x

отображения

H устойчива по Ляпунову (асимптотически устойчива).

Первая часть теоремы 3 очевидна, а вторая часть доказывается

совершенно аналогично доказательству теоремы 2 (с заменой нуле-

вого решения x(t) ≡ 0 на периодическое).