Леонов Г.А., Шумафов М.М. Проблемы стабилизации линейных управляемых систем

Подождите немного. Документ загружается.

131

Так как пара (A, b) по условию полностью управляема, то в силу

свойства IV

теоремы 1 из § 1, гл.II, ранг матрицы (d

∗

, d

∗

, ··· , d

∗

)

системы уравнений (25) равен n, и, тем самым,

det (d

∗

, d

∗

, ··· , d

∗

) 6= 0.

Следовательно, система уравнений (15) относительно вектора s име-

ет единственное решение в R

Таким образом, однозначно определяется вещественный вектор

s ∈ R

, удовлетворяющий соотношению (11).

Тем самым, теорема полностью доказана.

§ 6. Критерий Найквиста

Одним из эффективных критериев стационарной стабилизации

линейных систем является критерий Найквиста.

Рассмотрим линейную систему

˙x = Ax + bu, y = c

∗

x (x ∈ R

, u ∈ R

, y ∈ R

), (1)

где A, b, c — постоянные матрицы (порядков (n ×n), (n × m), (n × `)

соответственно).

Требуется найти такую обратную связь

u = s

∗

y, (2)

где s — постоянная (` × m)-матрица, чтобы замкнутая система (1),

(2) была асимптотически устойчивой.

Пусть W (p) — передаточная функция (значения которой суть мат-

рицы порядка ` × m) системы (1) (от входа u к выходу (−y))

W (p) = c

∗

(A − pI

)

−1

(где I

— единичная (n × n)-матрица). Пусть, далее,

∆

(p) = det (pI

− A), ∆

(p) = det [pI

− (A + bs

∗

)]

— характеристические многочлены матриц A (разомкнутой системы)

и A + bs

∗

(замкнутой системы).

Следующая лемма устанавливает связь между многочленами

∆

(p) и ∆

(p).

Лемма. Имеет место соотношение

∆

(p) = ∆

(p) det(I

+ s

∗

W (p)) (3)

132

Д о к а з а т е л ь с т в о. Используя следствие из леммы (см. §2,

гл. II), получим

∆

(p) = det (pI

− A) · det [I

+ (A − pI

)

−1

∗

] =

= ∆

(p) · det [I

+ s

∗

(A − pI

)

−1

b] =

= ∆

(p) · det (I

+ s

∗

W (p)).

Лемма доказана.

Предположим, что как у разомкнутой системы, так и у замкнутой

системы характеристические многочлены ∆

(p) и ∆

(p) не имеют

корней на мнимой оси. Тогда из формулы (3) следует, что

det [I

+ s

∗

W (iω)] 6= 0 при − ∞ < ω < +∞. (4)

Следовательно, мы можем определить число k

(целое) так:

2π

· ∆ Arg det (I

+ s

∗

W (iω))|

+∞

−∞

, (5)

где A Arg det(·)|

+∞

−∞

обозначает приращение функциии

ϕ(ω) = Arg det (I

+ s

∗

W (iω))

при изменении ω от −∞ до +∞ (под Arg z понимается некоторая

непрерывная ветвь многозначной функции arg z + 2πk, k ∈ Z, arg z

— главное значение аргумента: −π < arg z ≤ π).

Обозначим через k

и k

числа собственных значений матриц A

и A + bs

∗

, расположенных в правой полуплоскости с учетом их

кратностей.

Числа k

и k

называются степенями неустойчивости соответ-

ственно разомкнутой и замкнутой систем.

Теорема. Пусть матрицы A и A + bs

∗

не имеют собственных

значений на мнимой оси. Тогда справедливо соотношение

= k

− k

. (6)

133

Д о к а з а т е л ь с т в о. Применим к обеим частям равенства (3) фор-

мулу Эрмита—Михайлова (её применимость обеспечивается неравен-

ством (4) и условиями теоремы). В результате получим

π(n − 2k

) = π(n − 2k

) + 2πk

т.е. k

= k

− k

. Теорема доказана.

Из формулы (6) следует

Критерий Найквиста. Замкнутая система (1), (2) асимпто-

тически устойчива тогда и только тогда, когда

= k

. (7)

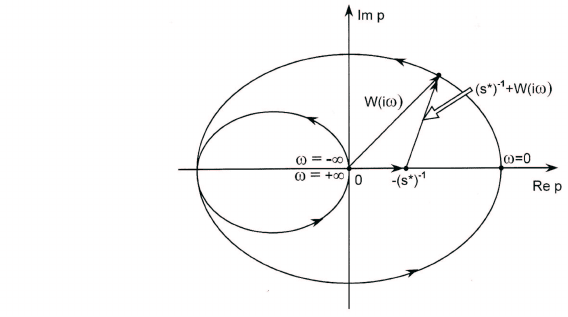
При m = 1 и ` = 1, т.е. когда вход u и выход y являются скаляр-

ными функциями (тогда и s

∗

— тоже скаляр), условие (4) означает,

что точка −(s

∗

)

−1

не лежит на годографе частотной характерстики

W (iω). Число k

, определяемое формулой (5), есть число оборотов

против часовой стрелки вектора [(s

∗

)

−1

+ W (iω)], начало которого

находится в точке −(s

∗

)

−1

, а конец — на годографе W (iω), или, что

то же самое, число оборотов годографа W (iω) вокруг точки −(s

∗

)

−1

при изменении ω от −∞ до +∞. По критерию Найквиста замкнутая

система (1), (2) асимптотически устойчива в том и только в том слу-

чае, если k

= k

. В этом и состоит геометрическая интерпретация

критерия Найквиста при m = ` = 1 (рис.10).

134

Рис.10. К геометрической интерпретации критерия Найквиста

(m = ` = 1) : k

= 1.

Основная ценность критерия Найквиста состоит в том, что он поз-

воляет судить об устойчивости замкнутой системы (1), (2) только по

частотной характеристике W(iω) системы (1), если даже неизвестно

аналитическое выражение для функции W (p).

§ 7. Стабилизируемость полностью наблюдаемой системы

в терминах разрешимости матричного уравнения

Лурье-Риккати

1. Постановка задачи

Рассмотрим линейную систему

˙x = Ax + bu, y = c

∗

x (x ∈ R

, u ∈ R

, y ∈ R

), (1)

где A, b и c — вещественные постоянные матрицы порядков n × n,

n × m и n × ` соответственно.

В § 5 мы рассмотрели возможность стабилизируемости системы

(1) в случае, когда выходом y системы (1) является вектор состоя-

ния x, т.е. y = x (c = I — единичная (n × n)-матрица). При этом

стабилизирующее управление u было построено по принципу полной

обратной связи: u = s

∗

x, где s — вещественная (n ×m)-матрица, так

что замкнутая система

˙x = (A + bs

∗

)x, x ∈ R

была асимптотически устойчивой (т.е. матрица A + bs

∗

— гурвице-

вой). Для этого достаточным условием стабилизируемости системы

(1) (или пары (A, b)) являлась ее полная управляемость.

Здесь мы рассмотрим вопрос о стабилизируемости системы (1) в

общем случае, когда матрица c не является единичной, т.е. когда

c 6= I (выходом системы (1) является не сам вектор состояния x, а

его проекции на ` линейно–независимых направлений c

, ··· , c

, где

∈ R

(k = 1, ··· , `) — столбцы матрицы c). Мы будем строить

управление u по принципу неполной обратной связи

u = s

∗

y (y ∈ R

), (2)

135

где s — вещественная постоянная (` × m)-матрица, так, чтобы за-

мкнутая система (1), (2), т.е. система

˙x = (A + bs

∗

)x (x ∈ R

)

была асимптотически устойчивой.

Другими словами, наша задача — стабилизировать тройку

(A, b, c), т.е. найти вещественную (` × m)-матрицу s такую, чтобы

матрица A + bs

∗

была гурвицевой.

Прежде чем приступить к решению сформулированной выше за-

дачи, мы сначала докажем два вспомогательных предложения.

2. Вспомогательные утверждения. Следующая лемма хорошо

известна.

Лемма 1. (Лемма А.М.Ляпунова.) Пусть A — гурвицева

(n × n)-матрица, а G — произвольная симметрическая матрица

∗

= G). Тогда матричное уравнение

∗

X + XA = G (X

∗

= X) (3)

относительно симметрической (n × n)-матрицы X имеет и при-

том единственное решение

X = −

+∞

∗

dt. (4)

Если G ≤ 0, то X ≥ 0, причем, при G < 0, X > 0.

(Условимся считать, что некоторая матрица Q ≥ 0 или

Q ≤ 0, если соответствующая ей квадратичная форма x

∗

Qx ≥ 0

или x

∗

Qx ≤ 0 для любого вектора x; аналогично, Q > 0 (Q < 0),

если x

∗

Qx > 0 (x

∗

Qx < 0) для любого вектора x 6= 0).

Д о к а з а т е л ь с т в о . По лемме об оценке нормы матричной

экспоненты (см. § 2, гл.I) имеем

k ≤ G

(α+ε)t

∀t ∈ [0, +∞), (5)

где α = max

Re λ

(A), λ

(A) (j = 1, ··· , n) — собственные числа мат-

рицы A, ε — любое положительное число, а C

— некоторая поло-

жительная константа. Так как по условию A — гурвицева и, следо-

вательно, λ

(A) < 0 (j = 1, ··· , n), то в силу произвольности ε > 0

136

можно считать α +ε < 0. Тогда, очевидно, из оценки (5) следует, что

интеграл (4) сходится.

Непосредственной подстановкой выражения (4) в (3) легко прове-

ряется, что (4) — решение уравнения (3). Действительно, учитывая

соотношение

∗

) = A

∗

) + (e

∗

)A,

получаем

∗

X + XA = −

∞

∗

) dt −

∞

∗

)A dt =

= −

+∞

∗

) dt = −e

∗

+∞

= G.

Покажем теперь, что решение (4) уравнения (3) единственное.

Предположим противное. Пусть Y — другое, отличное от X, решение

уравнения (3). Тогда для матрицы

Z = Y − X

имеем

∗

Z + ZA = 0. (6)

Рассматривая квадратичную форму

F (x) = x

∗

Zx, x ∈ R

и вычисляя ее производную

F в силу системы

˙x = Ax, (7)

на основании (6) получаем

F = ˙x

∗

Zx + x

∗

Z ˙x = x

∗

Zx + x

∗

ZAx = x

∗

Z + ZA)x = 0,

т.е.

F (x(t)) = 0 (∀t ≥ 0), (8)

где x(t) — решение уравнения (7) с начальным условием

x(0) = x

, x

∈ R

. Из равенства (8) имеем

F (x(t)) ≡ F (x

). (9)

137

Поскольку A — гурвицева матрица, то любое решение уравнения

(7) стремится к нулю: lim

t→∞

x(t) = 0 (это следует из формулы

x(t) = e

для решения уравнения (7)). Поэтому из (9) получаем:

F (x

) = 0 ∀x

∈ R

, т.е.

∗

= 0 ∀x

∈ R

Отсюда в силу произвольности вектора x

заключаем, что Z = 0,

т.е. Y = X.

Таким образом, решение (4) уравнения (3) единственно.

Если G ≤ 0, т.е. ξ

∗

Gξ ≤ 0 для любого вектора ξ, то из (4) имеем

∗

Xξ = −

+∞

ξ)

∗

G(e

ξ) dt ≥ 0, (10)

т.е. X ≥ 0.

Если же G < 0, то с учетом того, что матричная экспонента e

—

неособая матрица (см. следствие леммы 2, из § 2, гл.I ), будем иметь:

ξ)

∗

G(e

ξ) < 0 ∀ξ 6= 0.

Отсюда и из (10) получаем ξ

∗

Xξ > 0 т.е. X > 0. Лемма 1 доказана.

Лемма 2. Пусть (n × n)-матрицы A и H, где H = H

∗

, удовле-

творяют матричному неравенству

∗

H + HA ≤ −cc

∗

, (11)

где c — (n×`)-матрица, причем, пара (A, c) полностью наблюдаема.

Тогда:

1) матрица A не имеет собственных значений на мнимой оси;

2) матрица A гурвицева тогда и только тогда, когда H > 0.

Д о к а з а т е л ь с т в о . 1) Покажем, что матрица A не име-

ет собственных значений на мнимой оси. Предположим противное:

пусть λ

= iω, (ω ∈ R) — собственное значение матрицы A, а ξ

6= 0

— соответствующий ему собственный вектор, т.е.

Aξ

= λ

. (12)

Тогда вектор-функция

ξ(t) = ξ

iωt

138

будет решением уравнения

˙x = Ax (x ∈ R

). (13)

Рассмотрим квадратичную форму V (x) = x

∗

Hx и найдем ее про-

изводную в силу системы (13). Имеем

V = x

∗

H + HA)x. (14)

Так как

V (ξ(t)) ≡ ξ

∗

Hξ

= V (ξ

то

(ξ(t)) ≡ 0. (15)

Из матричного неравенства (11) (записанного в виде неравенства со-

ответствующих квадратичных форм) и соотношений (14) и (15) по-

лучим

0 ≡ ξ(t)

∗

H + HA)ξ(t) ≤ −(c

∗

)

∗

). (16)

Отсюда, с учетом того, что правая часть неравенства (16) неполо-

жительна, имеем

∗

= 0. (17)

Очевидно, что для матрицы

B = (A −λ

I, c

∗

)

в силу (12) и (17) справедливо равенство Bξ

= 0. Отсюда следует,

что rank B < n, поскольку ξ

6= 0. С другой стороны, поскольку пара

(A, c) по условию полностью наблюдаема, то по теореме двойствен-

ности Калмана (см. § 3, гл.II) пара (A

∗

, c) будет полностью управ-

ляемой и, следовательно, по свойству (V II

) теоремы 1 из § 1, гл.II

будем иметь:

rank (A − pI, c

∗

) = rank (A

∗

− pI, c) = n

для любого p ∈ C. Полученное противоречие доказывает утвержде-

ние 1) леммы.

2) Пусть A — гурвицева матрица. Возьмем произвольный вектор

∈ R

. Тогда

x(t, x

) = e

139

— решение уравнения (13) с начальным условием x(0) = x

. Исполь-

зуя оценку нормы экспоненты (см. лемму 2 из § 2, гл.I), будем иметь:

lim

t→+∞

x(t, x

) = 0. (18)

Учитывая неравенство (11), оценим производную

V из (14) (где

V = x

∗

Hx):

V ≤ −kc

∗

. (19)

Интегрируя неравенство (19) в пределах от t = 0 до t = ∞ вдоль

решения x(t) и учитывая соотношение (18), получим

= V (x

) ≥

+∞

∗

x(t, x

dt. (20)

Заметим, что c

∗

x(t, x

) 6≡ 0. Действительно, в противном случае име-

ли бы x

∗

exp(A

∗

t)c ≡ 0, что в силу свойства (II

) теоремы о крите-

риях управляемости (см. § 1, гл.II) означало бы неполную управля-

емость пары (A

∗

, c) или в силу теоремы о двойственности Калма-

на неполную наблюдаемость пары (A, c), что противоречит условию

леммы 2.

Следовательно, правая часть неравенства (20) положительна для

любого x

6= 0. Отсюда следует, что H > 0.

Обратно, пусть H > 0. Покажем, что тогда A — гурвицева. Пусть

λ — произвольное собственное значение матрицы A, а ξ 6= 0 — соот-

ветствующий ему собственный вектор, т.е. Aξ = λξ. Отсюда имеем:

∗

H + HA)ξ = (Aξ)

∗

Hξ + ξ

∗

H(Aξ) = 2(Re λ)ξ

∗

Hξ. (21)

Из неравенства (11), учитывая (21), получаем

2(Re λ)ξ

∗

Hξ ≤ −kc

∗

ξk

≤ 0. (22)

Так как ξ

∗

Hξ > 0, то из (22) имеем Re λ ≤ 0. Отсюда и из доказанно-

го выше утверждения 1) леммы 2 следует, что Re λ < 0, т.е. матрица

A — гурвицева. Лемма 2 доказана.

3. Теорема о стабилизируемости тройки (A, b, c) в терми-

нах разрешимости специального уравнения Лурье-Риккати.

Докажем сначала теорему дающую необходимое условие стабили-

зируемости системы (1).

140

Теорема 1 (необходимое условие стабилизируемости трой-

ки (A, b, c)([237])).Пусть система (1) стабилизируема. Тогда:

1) пары (A, b) и (A

∗

, c) стабилизируемы;

2) существуют вещественные (` ×m)- и (m ×n)-матрицы s и g

соответственно, такие, что

∗

+ b

∗

H = g, (23)

где H = H

∗

— вещественная неотрицательно определенная (n ×n)-

матрица, являющаяся решением матричного уравнения

∗

H + HA − Hbb

∗

H + cc

∗

+ g

∗

g = 0. (24)

Д о к а з а т е л ь с т в о . Пусть система (1) стабилизируема. То-

гда существует вещественная (` × m)-матрица s такая, что матрица

A + bs

∗

гурвицева. Отсюда следует, что пары (A, b) и (A

∗

, c) ста-

билизируемы со стабилизирующими матрицами s

∗

= s

∗

и s

∗

= sb

∗

т.е. выполняется условие 1) теоремы 1.

Так как матрица A+bs

∗

гурвицева, то по лемме 1 (А.М.Ляпунова)

существует симметрическая матрица H = H

∗

> 0 такая, что

(A + bs

∗

)

∗

H + H(A + bs

∗

) = −cc

∗

− css

∗

. (25)

Равенство (25) можно переписать так

∗

H + HA − Hbb

∗

H + cc

∗

+ (s

∗

+ b

∗

+ b

∗

H) = 0.

Отсюда, положив g = s

∗

+ b

∗

H, получим, что выполнено условие

2) теоремы 1. Теорема 1 доказана.

Замечание. Уравнение (24) (квадратное относительно матрицы

H ) называется во многих работах по теории управления матричным

алгебраическим уравнением Риккати. Очевидно, что уравнению (24)

удовлетворяют стационарные решения дифференциального уравне-

ния

= −Hbb

∗

H + (A

∗

H + HA) + (cc

∗

+ gg

∗

которое по аналогии с обычным дифференциальным уравнением Рик-

кати называют матричным дифференциальным уравнением Рикка-

ти.

Следующая теорема дает достаточное условие стабилизируемости

системы (1).