Леонов Г.А., Шумафов М.М. Проблемы стабилизации линейных управляемых систем

Подождите немного. Документ загружается.

101

строящейся, как показывают формулы (30), (31), по следующим пра-

вилам:

1) В п е р в у ю с т р о к у таблицы (32) записываются коэффи-

циенты многочлена a(p) (см. (1) и (25)) с ч е т н ы м и номерами.

2) В о в т о р у ю с т р о к у таблицы (32) записываются

коэффициенты многочлена a(p) с н е ч е т н ы м и номерами.

3) Ч т о б ы п о с т р о и т ь j-ю с т р о к у (j ≥ 3), нужно из

чисел (j −2)-й строки вычесть числа (j −1)-й строки, предваритель-

но умноженные на такое число, чтобы начальный элемент (первая

разность) обратился в нуль. Затем нужно, отбросив этот нулевой

элемент, сдвинуть получившуюся строку на один шаг влево.

Очевидно, что регулярный случай (r = n + 1 в (29)) имеет место

тогда и только тогда, когда первый столбец в схеме Рауса (32)

состоит из n + 1 отличных от нуля чисел.

Применяя теорему Штурма к ряду (29) в интервале (−∞, +∞),

получаем из (28):

V (−∞) − V (+∞) = n − 2m. (33)

Так как знак f

(+∞) := lim

ω→+∞

(ω) совпадает со знаком старшего

коэффициента, а знак f

(−∞) := lim

ω→−∞

(ω) отличается от этого

знака множителем (−1)

n−k+1

(j = 1, ··· , n + 1), то

V (+∞) = V (α

, β

, γ

, δ

, ···), (34)

V (−∞) = V (α

, −β

, γ

, −δ

, ···). (35)

(Здесь правые части обозначают число перемен знака в соответству-

ющем ряду чисел, стоящих в скобках.) Так как число перемен знака

последовательности, состоящей из n+1 чисел, не больше n и равно n,

когда знаки всех членов последовательности чередуются, то сумма

правых частей равенств (34) и (35) равна n, т.е.

V (+∞) + V (−∞) = n. (36)

Из равенств (33) – (36) получаем

m = V (α

, β

, γ

, δ

, ···). (37)

Итак, справедлива

102

Теорема 4. (Теорема Рауса.) Пусть имеет место регулярный

случай, т.е. первый столбец в схеме Рауса (32) состоит из n + 1

отличных от нуля чисел.

Тогда число корней вещественного многочлена a(p) степени n,

лежащих в правой полуплоскости Re p > 0 (p ∈ C) равно числу

перемен знака в первом столбце схемы Рауса.

Формула (37) при m = 0 дает достаточное условие того, чтобы

вещественный многочлен a(p) был устойчив (в регулярном случае).

Покажем, что это условие также необходимо для устойчивости

многочлена a(p). Пусть все корни многочлена a(p) имеют отрица-

тельные вещественные части (т.е. лежат в левой полуплоскости

Re p < 0). Тогда многочлен a(p) не имеет корней на мнимой оси и,

следовательно, справедлива формула (28), а значит, и формула (33)

(m = 0):

V (−∞) − V (+∞) = n. (38)

Очевидно, что

0 ≤ V (−∞) ≤ r − 1 ≤ n, 0 ≤ V (+∞) ≤ r − 1 ≤ n

(так как числа V (−∞) и V (+∞) определены для ряда (29)). Поэтому

равенство (38) возможно лишь тогда, когда r−1 = n, т.е. когда имеет

место регулярный случай (r = n + 1) и V (−∞) = n, V (+∞) = 0, т.е.

в силу (34) справедлива формула (37), где m = 0.

Таким образом, имеет место следующий критерий устойчивости

произвольного вещественного многочлена.

Критерий Рауса. Для того чтобы все корни вещественного мно-

гочлена a(p) имели отрицательные вещественные части (т.е. ле-

жали в левой полуплоскости Re p < 0) необходимо и достаточно,

чтобы 1) число элементов первого столбца схемы Рауса (32) было

равно n + 1 и 2) чтобы все они были отличными от нуля и одного

знака.

Как мы видим, а л г о р и т м Р а у с а для выяснения вопроса

о том, лежат ли все корни вещественного многочлена a(p) степени n

(и положительным старшим коэффициентам a

(см. (1)) в левой по-

луплоскости Re p < 0, весьма прост и основывается на составлении

с х е м ы (т а б л и ц ы) Р а у с а (32), которая строится по правилам

1), 2), 3) (см. выше). Многочлен a(p) в (1) устойчив тогда и только

103

тогда, когда первый столбец схемы Рауса состоит из n + 1 поло-

жительных чисел.

5. Критерий Гурвица. В этом пункте мы получим, пользуясь

теоремой 4 (Рауса), критерий устойчивости многочлена a(p) (см. (1))

в том виде, в каком он был установлен А.Гурвицем [228]. При изло-

жении будем следовать [48].

Пусть, как и выше, a(p) — произвольный вещественный много-

член (с положительным старшим коэффициентом), записанным в

виде (25).

Условимся считать, что коэффициенты α

= a

и β

= a

2k+1

определены при всех k ∈ Z, положив

= 0 при k < 0 или k >

n − 1

(Здесь [x] означает целую часть вещественного числа x.)

О п р е д е л е н и е 7. М а т р и ц е й Г у р в и ц а многочлена

a(p) называется (n × n)-матрица, имеющая вид

H =







. . . β

n−1

. . . α

n−1

0 β

. . . β

n−2

0 α

. . . α

n−2

0 0 β

. . . β

n−3

··· ··· ··· ··· ···







. (39)

(Обратим внимание, что первой (второй) строкой матрицы (39)

является вторая (первая) строка схемы Рауса (32).)

О п р е д е л е н и е 8. О п р е д е л и т е л я м и Г у р в и ц а

∆

, ··· , ∆

многочлена a(p) называются последовательные главные

миноры матрицы Гурвица H:

∆

= β

, ∆

0 β

, ···

Ниже нам понадобится понятие эквивалентности двух матриц M

и M

в следующем смысле.

104

О п р е д е л е н и е 9. Две матрицы M

= {α

}

= {β

} (i, j = 1, ··· , n) будем называть эквивалентными в том

и только в том случае, когда при любом s ≤ n в первых s строках

этих матриц соответствующие миноры s-го порядка равны между

собой, что будем записывать так:

1 2 ··· s

··· j

= M

1 2 ··· s

··· j

(s = 1, 2, ··· , n; 1 ≤ j

< j

< ··· < j

≤ n; здесь 1, 2, ··· , s — номера

строк, а j

, ··· , j

— номера столбцов соответствующих миноров

s-го порядка.

Рассмотрим р е г у л я р н ы й с л у ч а й , когда β

6= 0,

6= 0, δ

6= 0 ··· (т.е. все элементы в первом столбце схемы Рауса

(32) отличны от нуля).

Преобразуем матрицу Гурвица, вычитая из каждой строки с чет-

ным номером предыдущую строку, предварительно умноженную на

. Тогда в каждой четной строке мы получим, очевидно, соответ-

ствующим образом сдвинутую третью строку схемы Рауса:







. . . β

n−1

0 γ

. . . γ

n−2

0 β

. . . β

n−2

0 0 γ

. . . γ

n−3

0 0 β

. . . β

n−3

··· ··· ··· ··· ···







Полученную матрицу H

снова преобразуем (оставляя без изме-

нения первые две ее строки), вычитая из каждой строки (начиная с

третьей) с нечетным номером предыдущую, умноженную на

. В

результате в каждой нечетной строке (кроме первой) появится соот-

ветствующим образом сдвинутая четвертая строка схемы Рауса:







. . .

0 γ

. . .

0 0 δ

. . .

0 0 γ

. . .

0 0 0 δ

. . .

··· ··· ··· ··· ···







105

На следующем шаге аналогичным образом преобразуем все стро-

ки, кроме первых трех. В результате в четных строках, начиная с

четвертой, появится пятая строка схемы Рауса.

Продолжая этот процесс далее, мы получим из матрицы H тре-

угольную (n × n)-матрицу:

R =







. . .

0 γ

. . .

0 0 δ

. . .

··· ··· ··· ··· ···







. (40)

Матрицу (40) называют м а т р и ц е й Р а у с а .

Матрица Рауса получается (как это видно из сравнений (32) и

(40)) из схемы Рауса:

1) отбрасыванием первой строки,

2) сдвигом строк вправо так, чтобы их первые элементы пришлись

на главную диагональ,

3) пополнением нулями до квадратной матрицы порядка n × n.

Так как при описанных выше преобразованиях матрицы H мино-

ры s-го порядка в первых s строках (s = 1, 2, ··· , n) не изменяют

своих значений, то матрицы Гурвица H и Рауса R эквивалентны в

смысле определения 9, т.е.

1 2 ··· s

··· j

= R

1 2 ··· s

··· j

(41)

(s = 1, 2, ··· , n; 1 ≤ j

< j

< ··· < j

≤ n).

Эквивалентность (в смысле определения 9) матриц H и R поз-

воляет выразить все элементы матрицы R, т.е. все элементы схемы

Рауса (32), через миноры матрицы H и, следовательно, через коэф-

фициенты α

и β

данного многочлена a(p).

106

Действительно, давая s последовательно значения 1, 2, ··· , n, по-

лучим из (41):

= β

, H

= β

, H

= β

, ··· ,

1 2

= β

, H

1 2

1 3

= β

, H

1 2

1 4

= β

, ··· ,

1 2 3

= β

, H

1 2 3

1 2 4

= β

, H

1 2 3

1 2 5

= β

··· ··· ··· ··· ···











(42)

Отсюда имеем следующие выражения для элементов схемы Рауса

(32):

= H

, β

= H

, β

= H

, ··· ,

1 2

, γ

1 2

1 3

, γ

1 2

1 4

, ··· ,

1 2 3

1 2

, δ

1 2 3

1 2 4

1 2

, δ

1 2 3

1 2 5

1 2

, ··· ,

··· ··· ··· ··· ···











Из (42) получаем формулы для вычисления определителей

∆

, ··· , ∆

Гурвица:

∆

≡ H

= β

, ∆

≡ H

1 2

= β

∆

≡ H

1 2 3

= β

, ···

. (43)

Согласно формулам (43) р е г у л я р н ы й с л у ч а й (все чис-

ла β

, γ

, δ

··· отличны от нуля) имеет место тогда и только тогда,

когда все определители Гурвица отличны от нуля:

∆

6= 0, ∆

6= 0, ··· , ∆

6= 0. (44)

107

Из (43), с учетом неравенств (44), находим формулы, выражающие

элементы первого столбца схемы Рауса через определители Гурвица:

= ∆

, γ

∆

, δ

∆

, ··· . (45)

Учитывая равенства (45), из формулы (37) получаем, что число

m корней многочлена a(p) с положительной вещественной частью

равно

m = V (α

, β

, γ

, δ

, ···) = V (α

, ∆

∆

, ··· ,

∆

n−1

). (46)

С учетом формулы (46) теорема Рауса может быть сформулирована

так:

Теорема 5 (Рауса–Гурвица). Пусть все определители

∆

, ··· , ∆

Гурвица отличны от нуля.

Тогда число корней вещественного многочлена a(p) степени n,

лежащих в правой полуплоскости Re p > 0 (p ∈ C), равно

m = V (α

, ∆

∆

, ··· ,

∆

n−1

) (47)

(т.е. числу перемен знака в последовательности чисел, стоящих в

скобках в правой части равенства (47)).

При m = 0 формула (47) выражает достаточное условие устой-

чивости многочлена a(p) (при выполнении неравенств (44)).

Это условие также необходимо для устойчивости многочлена a(p).

Действительно, пусть все корни многочлена a(p) лежат в левой полу-

плоскости. Тогда, в силу критерия Рауса, все числа α

, β

, γ

, δ

, ···

отличны от нуля и одного знака. Следовательно, согласно (43)–(45)

имеет место неравенство (46), где m = 0.

Таким образом, установлен следующий критерий устойчивости мно-

гочлена a(p).

Критерий Гурвица. Для того чтобы все корни вещественного

многочлена a(p) степени n с положительным старшим коэффици-

ентом α

имели отрицательные вещественные части, необходимо

и достаточно, чтобы все определители Гурвица были положитель-

ными:

∆

> 0, ∆

> 0, ··· , ∆

> 0, (48)

108

т.е. (в исходных обозначениях a

(k = 0, 1, 2, ··· , n) коэффициентов

многочлена a(p), a

> 0)

> 0,

0 a

> 0,

··· , det H ≡

··· 0

0 a

··· 0

0 a

··· 0

··· ··· ··· ··· ···

··· ··· ··· ··· a

> 0,











(49)

(где принято a

= 0 при k < 0 или k > n ).

Условия (48) или, что то же самое, условия (49) называются усло-

виями Гурвица.

Замечание 1. Условия (49) иногда называются у с л о в и я м и

Р а у с а–Г у р в и ц а .

Замечание 2. Если коэффициенты многочлена a(p) заданы чис-

ленно, то формулы (43) дают наиболее простой способ вычисления

определителей Гурвица, сводя это вычисление к составлению схемы

Рауса.

Замечание 3. Для выяснения устойчивости вещественных много-

членов, коэффициенты которых заданы как конкретные числа, алго-

ритм Рауса удобнее критерия Гурвица. Однако для изучения устой-

чивости многочленов с коэффициентами, зависящими от парамет-

ров, удобнее критерий Гурвица.

Примеры.

1) Для многочлена второй степени (n = 2) условия Рауса-Гурвица

имеют вид

> 0,

> 0

или, что то же самое,

> 0, a

> 0.

109

Последние совпадают с условиями устойчивости многочлена вто-

рой степени, полученными с помощью критерия Эрмита-Михайлова

(см. п.3, пример 1)).

2) Для многочлена третьей степени (n = 3) условия Рауса-Гур-

вица запишутся так:

> 0,

0 a

> 0

или

> 0, a

> a

, a

− a

) > 0.

Вместе с условием a

> 0 последние неравенства эквивалентны сле-

дующим неравенствам

> 0, a

> a

которые совпадают с условиями устойчивости многочлена третьей

степени, полученными выше в примере 2) (см. п.3) с помощью кри-

терия Эрмита-Михайлова.

§ 3. Задача линейной стабилизации

Пусть на вход линейной системы

˙x = Ax + bu, y = c

∗

x (x ∈ R

, u ∈ R

, y ∈ R

), (1)

где A, b и c — вещественные постоянные матрицы порядков n × n,

n × m и n × ` соответственно, подается управление u в зависимости

от измеренных сигналов выходов — координат вектора y: u = s

∗

y, где

s — некоторая, вообще говоря, зависящая от времени t переменная

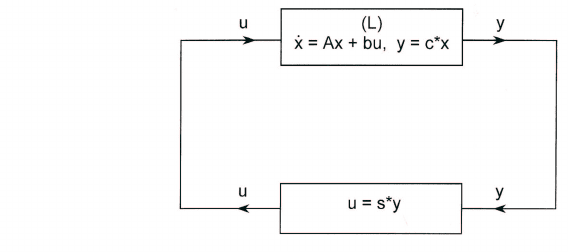
(` ×m)-матрица. Тогда говорят о линейном управлении по принципу

обратной связи (рис. 9).

Если в каждый момент времени измерению доступны все коорди-

наты вектора состояния x системы (в этом случае в системе (1) c —

единичная (n × n)-матрица, так что y = x), то говорят, что управле-

ние построено по принципу полной обратной связи. Если же изме-

рению доступны только проекции вектора состояния x на ` (` < n)

110

линейно-независимых направлений c

, . . . , c

, то говорят, что управ-

ление построено по принципу неполной обратной связи (в этом слу-

чае в системе (1) вектор y = c

∗

x, где c = (c

, . . . , c

) — матрица,

столбцами которой являются векторы c

, . . . , c

Рис. 9. Управление по принципу обратной связи.

Задача линейной стабилизации системы (1) состоит в том, чтобы

построить управление

u = s(t)

∗

y, y = c

∗

x (2)

с (`×m)-матрицей s(t), при котором система (1), замкнутая обратной

связью (2), т.е. система

˙x =

A + b(cs(t))

∗

x (3)

асимптотически устойчива (в целом).

Управление (2), решающее задачу стабилизации системы (1), на-

зывается стабилизирующим.

О п р е д е л е н и е. Система (1) называется с т а б и л и з и р у е-

м о й (или т р о й к а (A, b, c) называется с т а б и л и з и р у е м о й),

если существует хотя бы одно ее стабилизирующее управление (2).

В частности, когда в (2) c – единичная матрица, т.е. управле-

ние построено по принципу полной обратной связи, то говорят о

с т а б и л и з и р у е м о с т и п а р ы (A, b).

Если матрица s(t) в (2) постоянная: s(t) ≡ s

= const , то бу-

дем говорить о линейной стационарной стабилизации системы (1),