Леонов Г.А., Шумафов М.М. Проблемы стабилизации линейных управляемых систем
Подождите немного. Документ загружается.


81
(это неравенство было доказано для t
0
= 0, но, очевидно, оно верно
также и для любого t
0
6= 0), где ν — произвольное положительное
число, C
ν
> 0 — некоторая константа, зависящая от ν, а
α = max
j
Re λ
j
.
В силу (7) α < 0. Выберем ν > 0 так, чтобы α + ν < 0. Тогда из (9)
будем иметь
ke
A(t−t
0
)
k ≤ M ∀t ∈ [t
0
, +∞),
где M — некоторая положительная константа. Отсюда и из формулы
(8) получаем
kx(t)k ≤ ke
A(t−t
0
)
k · kx
0
k ≤ M · kx
0
k. (10)
Пусть ε — произвольное положительное число. Тогда если
kx
0
k <
ε
M
=: δ,
то в силу (10)
kx(t)k < ε для всех t ∈ [t
0
, +∞).
Поэтому тривиальное решение x(t) ≡ 0 (положение равновесия) си-
стемы (6) устойчиво по Ляпунову (продолжаемость решения x(t) на
бесконечный интервал [t
0
, +∞) следует из его вида (8)).
Так как в силу (8) и (9)
kx(t)k ≤ C
ν
e
(α+ν)(t−t
0
)
kx
0
k,
то, учитывая, что α + ν < 0, получаем
lim
t→+∞
x(t) = 0.
Следовательно, тривиальное решение x(t) ≡ 0 асимптотически устой-
чиво в целом. Достаточность условия теоремы доказана.
2. Н е о б х о д и м о с т ь. Пусть положение равновесия x = 0 систе-
мы (6) асимптотически устойчиво в целом. Покажем сначала, что
Re λ
j
≤ 0 (j = 1, . . . , m). (11)
Действительно, допустим, что существует собственное число λ
r
(1 ≤ r ≤ m) такое, что Re λ
r
= α
r
> 0. Тогда система (6) имеет
нетривиальное решение
η(t) = e
λ
r
t
ξ
r
,
82
где ξ
r
— собственный вектор матрицы A, соответствующий собствен-
ному числу λ
r
. Отсюда
kη(t)k = |e
λ
r
t
| · kξ
r
k = e
α
r
t
· kξ
r
k → +∞ при t → +∞.
Последнее противоречит условию асимптотической устойчивости
в целом положения равновесия системы (6). Таким образом, имеют
место неравенства (11).
Предположим теперь, что найдется хотя бы одно собственное чис-
ло λ
s
(1 ≤ s ≤ m) такое, что
Re λ
s
= 0,
т.е. λ
s
= iβ
s
, β
s
∈ R (i — мнимая единица). Тогда система (6) имеет
решение (комплексное)
ϕ(t) = e
λ
s
t
ξ
s
= (cos β
s
t + i sin β
s
t)ξ
s
,
где ξ
s
— собственный вектор матрицы A, соответствующий собствен-
ному числу λ
s
. Отсюда
kϕ(t)k = kξ
s
k 6= 0,
и, значит, ϕ(t) 6→ 0 при t → +∞, что противоречит асимптотической
устойчивости в целом тривиального решения x(t) ≡ 0. Следователь-
но,
Re λ
j
< 0 (j = 1, . . . , m).
Теорема 1 доказана полностью.
О п р е д е л е н и е 4. Если каждое решение линейной системы
(6) асимптотически устойчиво в целом, то систему (6) называют
асимптотически устойчивой в целом.
Следующая теорема сводит вопрос об асимптотической устойчиво-
сти системы (6) к асимптотической устойчивости нулевого решения
x(t) ≡ 0.
Теорема 2. Для асимптотической устойчивости в целом ли-
нейной системы (6) необходимо и достаточно, чтобы тривиальное
решение x(t) ≡ 0 этой системы было асимптотически устойчивым
в целом.
Д о к а з а т е л ь с т в о. Необходимость условия теоремы очевидна.
83
Докажем достаточность. Пусть тривиальное решение x(t) ≡ 0
асимптотически устойчиво в целом. Если η(t) — некоторое фиксиро-
ванное, но произвольное решение системы (6), а x(t) — любое другое
ее решение, то в силу (8)
x
(
t
) =
e
A(t−t
0
)
x
0
, η
(
t
) =
e
A(t−t
0
)
η
0
,
где x
0
∈ R
n
, η
0
∈ R
n
и x(t) − η(t) = e
A(t−t
0
(x
0
− η
0
). (Заметим, что
разность x(t) − η(t) есть тоже решение системы (6).)
Далее, повторяя рассуждения доказательства достаточности тео-
ремы 1 установим, что решение η(t) асимптотически устойчиво в це-
лом.
Теорема 2 доказана.
Из теорем 1 и 2 следует следующая
Теорема 3. (Критерий асимптотической устойчивости ли-
нейной системы.) Линейная система (6) асимптотически устой-
чива в целом тогда и только тогда, когда все собственные чис-
ла λ
j
(A) матрицы A имеют отрицательные вещественные части:
Re λ
j
(A) < 0 (j = 1, . . . , n).
В дальнейшем будем называть матрицу A устойчивой или гур-
вицевой, если все ее собственные числа λ
j
(A) лежат в левой полу-
плоскости: Re λ
j
(A) < 0 (j = 1, . . . , n).
Отметим, что утверждение теоремы 2 справедливо также и для
линейных систем с переменной матрицей: A = A(t). А именно, имеет
место
Теорема 4. Линейная система
˙x = A(t)x (12)
с (вещественной) кусочно-непрерывной на интервале I
+
t
= (a, +∞)
(a ∈ R) матрицей-функцией A(t) асимптотически устойчива (в
целом) тогда и только тогда, когда тривиальное решение x(t) ≡ 0
этой системы асимптотически устойчиво (в целом).
Систему (12) (как и (6)) называют асимптотически устойчивой
(в целом), если все ее решения асимптотически устойчивы (в целом).
Д о к а з а т е л ь с т в о т е о р е м ы 4. Необходимость условия тео-
ремы очевидна.
Докажем достаточность. Пусть тривиальное решение x(t) ≡ 0
системы (12) асимптотически устойчиво. Тогда оно устойчиво (по
84
Ляпунову), т.е. по заданному числу ε > 0 можно найти такое δ(ε),
что для любого решения x(t) системы (12) с начальным условием
x(t
0
) = x
0
(t
0
∈ I
+
t
, x
0
∈ R
n
):
kx
0
k < δ(ε), (13)
будем иметь
kx(t)k < ε для всех t ∈ [t
0
, +∞). (14)
Пусть теперь η(t) — произвольное решение системы (12). Для любого
другого решения x(t) системы (12) разность (как легко проверить)
z(t) = x(t) − η(t) тоже есть решение этой системы. Следовательно,
из неравенства
kx(t
0
) − η(t
0
)k < δ(ε),
в силу (13), (14), вытекает неравенство
kx(t) − η(t)k < ε ∀t ∈ [t
0
, +∞).
Последнее означает, что решение η(t) устойчиво по Ляпунову (в силу
замечания 1 из п.1 все решения x(t) системы (12) продолжаемы на
интервал [t
0
, +∞) ).
Так как для произвольного решения x(t) системы (12) (в силу
асимптотической устойчивости x(t) ≡ 0)
lim
t→+∞
x(t) = 0,
то и
lim
t→+∞
kx(t) − η(t)k = 0.
Следовательно, решение η(t), а вместе с ним и система (12) (в силу
произвольности η(t)), асимптотически устойчиво в целом. Теорема 4
доказана.
§ 2. Алгебраические критерии устойчивости
1. Проблема Рауса–Гурвица
В связи с доказанным в § 1 критерием асимптотической устойчи-
вости линейных дифференциальных систем (теорема 3) возникает
85
следующая алгебраическая задача (так называемая проблема Рауса–
Гурвица [48,92,113,135,228,276]): требуется узнать, лежат ли все кор-
ни данного многочлена в левой полуплоскости комплексного пере-
менного. Другими словами, требуется установить необходимые и
достаточные условия, при которых все корни данного алгебраиче-
ского многочлена имеют отрицательные вещественные части.
Эта проблема широко обсуждалась в литературе (подробное и де-
тальное описание алгоритмов, связанных с проблемой Рауса–Гурвица
можно найти, например, в [48,86,92,113,135]).
Здесь мы докажем наиболее распространенные критерии Эрмита-
Михайлова, Рауса и Гурвица, позволяющие дать положительный от-
вет на поставленный выше вопрос.
2. Необходимое условие устойчивости многочлена. Устано-
вим вначале простое необходимое условие устойчивости многочлена.
Рассмотрим многочлен степени n с вещественными коэффициен-
тами
a(p) = a
0
p
n
+ a
1
p
n−1
+ . . . + a
n
(a
k
∈ R, k = 0, . . . , n). (1)
О п р е д е л е н и е 1 . М н о г о ч л е н a(p) называется у с т о й-
ч и в ы м или г у р в и ц е в ы м , если все его корни имеют отрица-
тельные вещественные части, т.е. лежат по левую сторону от
мнимой оси плоскости комплексного переменного.
Устойчивые многочлены обычно называют м н о г о ч л е н а м и
(п о л и н о м а м и) Г у р в и ц а.
Теорема 1. (Теорема Стодолы.) Если многочлен a(p) в (1) с
a
0
> 0 устойчив, то все его коэффициенты положительны.
Д о к а з а т е л ь с т в о. Пусть p
j
, ¯p
j
= α
j
±iβ
j
(j = 1, . . . , `) — ком-
плексные корни (β
j
6= 0) (i – мнимая единица) и p
s
= γ
s
(s = 1, . . . , r)
— вещественные корни многочлена (1). Обозначим через µ
j
(j =
1, . . . , `) кратность корня p
j
= α
j
+ iβ
j
(так как коэффициенты мно-
гочлена a(p) действительны, то сопряженный корень ¯p
j
= α
j
− iβ
j
имеет тоже ту же кратность µ
j
). Через ν
s
обозначим кратность ве-
щественного корня p
s
= γ
s
. Тогда
`
X
j=1
2µ
j
+
r
X
s=1
ν
s
= n.
86
Используя известное разложение многочлена a(p) на вещественные
линейные двучлены (соответствующие его вещественным корням γ
s
)
и вещественные трехчлены (соответствующие парам сопряженных
корней α
j
± iβ
j
), получаем
a(p) = a
0
`
Y
j=1
(p − α
j
− iβ
j
)
µ
j
(p − α
j
+ iβ
j
)
µ
j
r
Y
s=1
(p − γ
s
)
ν
s
или
a(p) = a
0
`
Y
j=1
(p
2
− 2α
j
p + α
2
j
+ β
2
j
)
µ
j
r
Y
s=1
(p − γ
s
)
ν
s
. (2)
В силу условия теоремы 1 α
j
< 0, γ
s
< 0. Поэтому коэффициенты во
всех двучленах и трехчленах в правой части равенства (2) положи-
тельны и, следовательно, положительными будут и коэффициенты
многочлена a(p). Теорема 1 доказана.
Замечание. Условия теоремы Стодолы являются лишь необхо-
димыми, но вовсе, не достаточными для устойчивости многочлена
произвольной степени n > 2. Ниже, в примерах, будет показано, что
условия теоремы Стодолы для многочлена второй степени являются
и достаточными для его устойчивости, а для многочленов третьей
степени — нет, т.е. из положительности его коэффициентов, вообще
говоря, не следует его устойчивость.
3. Критерий Эрмита-Михайлова. Пусть m — число нулей (с
учетом их кратностей) многочлена (1) с положительной веществен-
ной частью. Предположим, что многочлен a(p) не имеет корней на
мнимой оси, т.е. a(iω) 6= 0 ∀ω ∈ R. Тогда можем определить функ-
цию
ϕ(ω) = Arg a(iω), (3)
где под Arg p понимается некоторая непрерывная ветвь многознач-
ной функции
arg p ± 2kπ, k ∈ Z
(arg p — главное значение аргумента: −π < arg p ≤ π). Это означает,
что при переходе годографа многочлена a(p) через луч
{Re p ≤ 0, Im p = 0} на комплексной плоскости при ω = ω
0
берем
ту ветвь функции (3), которая обеспечивает непрерывность такого
87
перехода, т.е. непрерывность функции ϕ(ω) в точке ω
0
. Не умаляя
общности, можно считать, что ϕ(0) = 0.
О п р е д е л е н и е 2. Множество точек {p ∈ C : p = a(iω),
ω ∈ R} комплексной плоскости C называется годографом многочле-
на a(p). Иногда этот годограф называют годографом Михайлова или
амплитудно-фазовой характеристикой многочлена a(p).
Через ∆ϕ(ω)
¯
¯
+∞
−∞
будем обозначать приращение функции ϕ(ω), ко-
гда аргумент ω изменяется от −∞ до +∞.
Имеет место следующее утверждение.
Теорема 2. Для любого многочлена
a(p) = a
0
p
n
+ a
1
p
n−1
+ . . . + a
n
, a
0
> 0 (a
k
∈ R, k = 0, ··· , n),
не имеющего корней на мнимой оси (a(iω) 6= 0 ∀ω ∈ R), справедлива
следующая ф о р м у л а Э р м и т а — М и х а й л о в а
∆ϕ(ω)
¯
¯
+∞
−∞
≡ ∆ Arg a(iω)
¯
¯
+∞
−∞
= π(n − 2m), (4)
где m — число корней многочлена a(p) в правой полуплоскости с
учетом их кратностей.
Д о к а з а т е л ь с т в о . Пусть λ
j
(j = 1, ··· , m) и ρ
`
(` = 1, ··· , n − m) — нули многочлена a(p) с положительными и
отрицательными вещественными частями, соответственно (каждый
нуль считается столько раз, какова ее кратность).
Представив многочлен a(p) в виде произведения
a(p) = a
0
m
Y
j=1
(p − λ
j
) ·
n−m
Y
`=1
(p − ρ
`
),
и затем, применив известную теорему об аргументе произведения
комплексных чисел (так как по условию теоремы a(iω) 6= 0 для лю-
бого ω ∈ (−∞, +∞), то при p = iω, −∞ < ω < +∞, все сомножители
правой части последнего равенства ненулевые), получим следующее
равенство:
∆ϕ(ω)|
+∞
−∞
≡ ∆Arg a(iω)|
+∞
−∞
= ∆Arg a
0
|
+∞
−∞
+
+
P
m
j=1
∆Arg (iω − λ
j
)|
+∞
−∞
+
P
n−m
`=1
∆Arg (iω − ρ
`
)|
+∞
−∞
.
(5)
Очевидно,
∆Arg a
0
|
+∞
−∞
= 0.
88
Вычислим
∆Arg (iω − λ
j
)|
+∞
−∞
, ∆Arg (iω −ρ
`
)|
+∞
−∞
.
Для этого сначала рассмотрим на комплексной плоскости числа
λ
j
, iω, iω − λ
j
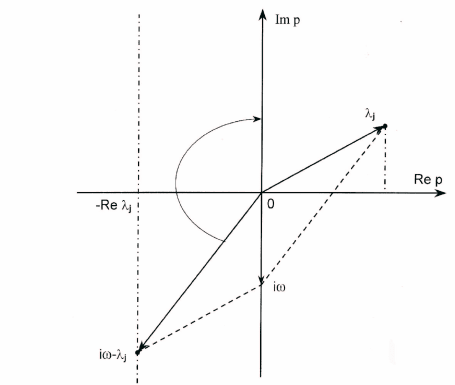
и соответствующие им векторы (рис. 6)
Рис. 6. К доказательству теоремы 2: Re λ
j
> 0.
Вектор, соответствующий числу iω −λ
j
, при увеличении ω от −∞
до +∞ поворачивается монотонно по часовой стрелке, при этом ко-
нец этого вектора скользит вверх, все время оставаясь на прямой
Re p = −Re λ
j
, так, как это показано на рис.6. Поэтому,
∆Arg (iω − λ
j
)|
+∞
−∞
= −π (j = 1, ··· , m).
Рассмотрим теперь на комплексной плоскости числа ρ
`
, iω, iω −ρ
`
и соответствующие им векторы (рис.7).
Вектор, соответствующий числу iω −ρ
`
, при увеличении ω от −∞
до +∞ поворачивается монотонно против часовой стрелки, причем
конец этого вектора скользит вверх, все время оставаясь на прямой
Re p = −Re ρ
`
, так, как это показано на рис.7. Следовательно,
∆Arg (iω − ρ
`
)|
+∞
−∞
= π (k = 1, ··· , n − m).

89
Рис. 7. К доказательству теоремы 2: Re ρ
`
< 0
Из последних двух равенств и разложения (5) следует, что
∆ϕ(ω)|
+∞
−∞
= −mπ + (n − m)π = π(n − 2m).
Таким образом, установлена формула (4) и, тем самым, доказана
теорема 2.
Из теоремы 2 следует
Критерий Эрмита—Михайлова. Пусть многочлен a(p) в (1)
степени n с a
0
> 0 не имеет корней на мнимой оси, т.е.
a(iω) 6= 0 ∀ω ∈ R. Тогда для устойчивости многочлена a(p) необхо-
димо и достаточно, чтобы
∆ϕ(ω)
¯
¯
+∞
−∞
= nπ. (6)
Действительно, полагая m = 0 в формуле (4), получим (6).
Замечание 1. В силу вещественности коэффициентов a
r
(r = 0, . . . , n) многочлена a(p) справедливы следующие равенства:
Re a(¯p) = Re a(p) = Re a(p),
Im a(¯p) = Im a(p) = −Im a(p)
(где ¯z — сопряженное для z). В частности, при p = iω имеем
Re a(−iω) = Re a(iω),
Im a(−iω) = −Im a(iω).
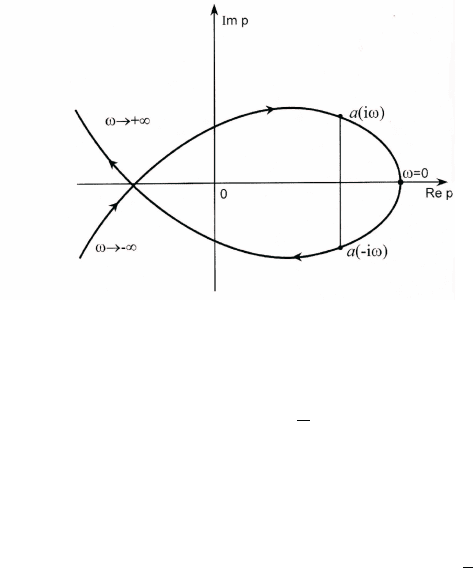
90
Отсюда следует, что годограф многочлена a(p) симметричен относи-
тельно вещественной оси (рис.8).
Рис. 8. Годограф многочлена a(p)
Поэтому вместо равенства (6) можно записать следующее условие:
∆ϕ(ω)
¯
¯
+∞
0
= n ·
π
2
. (7)
Замечание 2. Пусть m = 0, т.е. многочлен a(p) — устойчив (все
нули многочлена a(p) расположены в левой полуплоскости.) Тогда,
как было отмечено в процессе доказательства теоремы 2, для много-
члена a(p) вектор a(iω) при увеличении ω от −∞ до +∞ монотонно
поворачивается против хода часовой стрелки на угол n ·
π
2
. Так как
a(0) = a
n
> 0 (в силу теоремы Стодолы это необходимо), то годо-
граф Михайлова многочлена a(p), выходя из точки a
n
положитель-
ной полуоси {Re p > 0, Im p = 0}, при возрастании ω от 0 до +∞
будет последовательно пересекать полуоси {Re p = 0, Im p > 0},
{Re p < 0, Im p = 0}, {Re p = 0, Im p < 0}, проходя через n квад-
рантов.
Обратно, если годограф Михайлова многочлена a(p) степени n
без чисто мнимых корней, выходя из точки a(0) = a
n
> 0 поло-
жительной полуоси {Re p > 0, Im p = 0}, при возрастании ω от 0
до +∞ последовательно по одному разу пересекает n − 1 полуосей
{Re p = 0, Im p > 0}, {Re p < 0, Im p = 0} , . . . асимптотически стре-
мясь к n-й полуоси, то угол поворота вектора a(iω), очевидно, равен
