Леонов Г.А., Шумафов М.М. Проблемы стабилизации линейных управляемых систем
Подождите немного. Документ загружается.

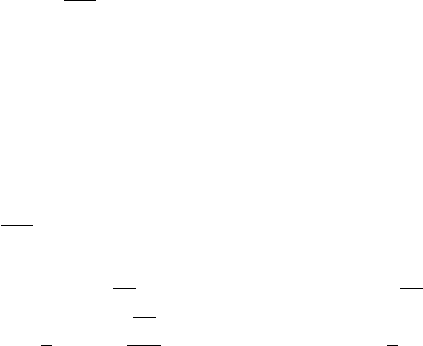
51
где ξ
0
∈ C
m
— произвольный вектор, и повторяя рассуждения, про-
веденные для функции ϕ(p) (см. п.2), получим в силу свойства един-
ственности аналитической функции, что ψ(p) ≡ 0 для всех точек p
комплексной плоскости, за исключением собственных значений λ
j
(A)
матрицы A.
Имеет место представление (см., например, [184, с.50, § 2, гл.I]),
e
At
=
1
2πi
I
Γ
(pI − A)
−1
e
pt
dp (t ∈ R), (20)
где Γ — окружность, содержащая внутри себя все собственные зна-
чения λ
j
(A) матрицы A и ориентированная в положительном на-
правлении (т.е. область, ограниченная Γ, во время обхода Γ остается
слева) (i — мнимая единица). Из (20) и (19), где Ω
0
= C\{λ
j
(A)},
получаем
z
∗
0
e
At
b =
1
2πi
I
Γ
z
∗
0
(pI − A)
−1
be
pt
dp = 0 ∀t ∈ R (z
0
6= 0).
Отсюда следует свойство (II
0
y
), которое эквивалентно (II
y
). Тем са-
мым, установлено свойство (II
y
).
6. Импликация (I
y
) ⇒ (III
y
). Пусть выполнено (I
y
), т.е. суще-
ствует ненулевой вектор z
0
∈ R
n
такой, что
z
∗
0
A
k
b = 0 (k = 0, 1, . . . , n − 1). (21)
Пусть
det(pI − A) = p
n
+ d
1
p
n−1
+ . . . + d
n
.
По теореме Гамильтона—Кэли [48]
A
n
+ d
1
A
n−1
+ . . . + d
n
I
n
= O
n
, (22)
где O
n
, I
n
— нулевая и единичная (n × n)-матрицы соответствен-
но. Умножая обе части равенства (22) последовательно на A, A
2
, . . .,
получим
A
n+1
+ d
1
A
n
+ . . . + d
n
A = O
n
,
A
n+2
+ d
1
A
n+1
+ . . . + d
n
A
2
= O
n
,
. . . . . . . . . . . . . . . . . . . . .
(23)
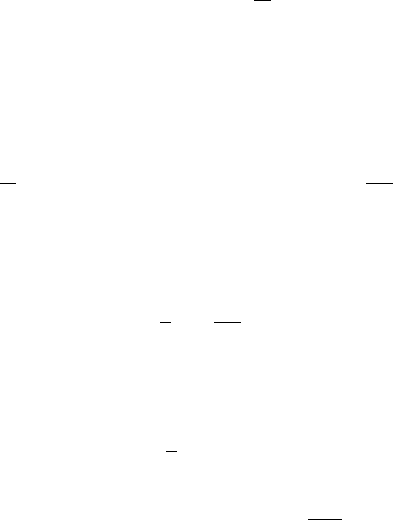
52
Из (22) и (23) следует, что матрицы A
n
, A
n+1
, A
n+2
, . . . являются ли-
нейными комбинациями матриц I
n
, A, A
2
, . . . , A
n−1
:
A
k
=
n−1
X
i=0
α
(k)
i
A
i
(k = n, n + 1, . . .).
Поэтому
z
∗
0
A
k
b =
n−1
X
i=0
α
(k)
i
z
∗
0
A
i
b = 0 (k = n, n + 1, . . .).
Итак, с учетом (21), имеем
∃ z
0
∈ R
n
, z
0
6= 0 : z
∗
0
A
k
b = 0 (k = 0, 1, 2, . . .). (24)
Разложим матричную функцию R(p) = (pI −A)
−1
в ряд по степе-
ням 1/p. Очевидно,
(pI − A)
−1
= p
−1
µ
I −
A
p
¶
−1
.
Очевидно, что если λ — собственное значение матрицы A, то λ/p
— собственное значение матрицы A/p. Поэтому при достаточно боль-
ших |p| все собственные значения матрицы A/p будут лежать внутри
единичного круга и, следовательно, имеет место разложение ([56])
µ
I −
A
p
¶
−1
= I + p
−1
A + p
2
A
2
+ . . . =
∞
X
k=0
A
k
p
k
, (25)
причем ряд (25) сходится при |p| > |Λ|, где Λ — максимальное по
модулю собственное значение матрицы A. Поэтому
R(p) = (pI − A)
−1
=
1
p
∞
X
k=0
A
k
p
k
, (|p| > |Λ|). (26)
Учитывая (24), из (26) получаем, что существует ненулевой вектор
z
0
∈ R
n
:
z
∗
0
(pI − A)
−1
b =
1
p
∞
X
k=0
p
−k
z
∗
0
A
k
b = 0
для любого p ∈ ∆, где ∆ — внешность круга радиуса |Λ| с центром
в точке 0. Последнее означает, что выполнено (III
y
).

53
7. Импликация (V
y
) ⇒ (I
y
). Прежде всего заметим, что матрица
K, определяемая формулой (9), неотрицательно определена. Дей-
ствительно, для любого z ∈ R
n
имеем
z
∗
Kz =
t
2
Z
t
1
(z
∗
e
At
b)(z
∗
e
At
b)
∗
dt =
t
2
Z
t
1
|z
∗
e
At
b|
2
dt ≥ 0, (27)
т.е. z
∗
Kz ≥ 0 ∀z ∈ R
n
.
Пусть теперь справедливо (V
y
), т.е. существуют такие числа
t
1
< t
2
и существует такой ненулевой вектор z
0
∈ R
n
, что
z
∗
0
Kz
0
= 0. С учетом последнего равенства, из (27) получаем, что
t
2
Z
t
1
|z
∗
0
e
At
b|
2
dt = 0.
Последнее равенство необходимо влечет тождество
z
∗
0
e
At
b ≡ 0 на [t
1
, t
2
]. (28)
В силу свойства единственности аналитической функции из (28) сле-
дует (см. рассуждения п.2), что справедливо также тождество
z
∗
0
e
At
b ≡ 0 на (−∞, +∞). (29)
Дифференцируя последовательно тождество (29), имеем
z
∗
0
A
k
e
At
b ≡ 0 ∀t ∈ (−∞, +∞) (k = 0, 1, 2, . . .). (30)
Положив в равенстве (30) t = 0, получим
z
∗
0
A
k
b = 0 (k = 0, 1, 2, . . .),
где z
0
6= 0, т.е. не выполняются соотношения (4). Тем самым уста-
новлено свойство (I
y
).
8. Импликация (п.упр.) ⇒ (V
y
). Докажем эквивалентное утвер-
ждение: (V
y
) ⇒ (п.упр.).
Предположим, что имеет место (V
y
), т.е. K > 0 для любых t
1
< t
2
.
Пусть t
0
, t
1
∈ R — произвольные числа, а x
0
, x
1
∈ R
n
— произвольные
векторы. Требуется найти такое управление u(t), t ∈ [t
0
, t
1
], чтобы
для соответствующего решения x(t) системы (1) были справедливы
равенства:
x(t
0
) = x
0
, x(t
1
) = x
1
. (31)

54
Будем искать требуемое управление u(t) в виде
u(t) = b
∗
e
A
∗
(t
1
−t)
c, (32)
где c ∈ R
n
— некоторый постоянный вектор, подлежащий определе-
нию. Тогда, поступая аналогично п.4, имеем:
x
1
− e
A(t
1
−t
0
)
x
0
=
t
1
Z
t
0
e
A(t
1
−s)
bb
∗
e
A
∗
(t
1
−s)
c ds =
µ
t
1
−t
0
Z
0
e
At
bb
∗
e
A
∗
t
dt
¶
c,
т.е. получаем уравнение
x
1
− e
AT
x
0
= K
T
c, (33)
где T = t
1
− t
0
, K
T
=
Z
T
0
e
At
bb
∗
e
A
∗
t
dt, для определения вектора c.
Так как по условию матрица K
T
> 0, то det K
T
6= 0. Следователь-
но, существует обратная матрица K
−1
T
. Из уравнения (33) находим
c = K
−1
T
(x
1
− e
AT
x
0
). (34)
При указанном выборе управления в виде (32), где c определяется
согласно (34), соответствующее решение x(t) удовлетворяет услови-
ям (31). Следовательно, пара (A, b) полностью управляема.
9. Эквивалентность (V III
y
) ⇐⇒ (п.упр.).
9.1. Пусть справедливо утверждение (V III
y
), т.е. существует неосо-
бая матрица S такая, что имеют место равенства (10) или (11).
Сделаем в системе (1) линейное преобразование
x = Sξ.
Получим систему
½
˙
ξ =
˜
Aξ +
˜
bu,
y = ˜c
∗
ξ,
(35)
где
˜
A = S
−1
AS,
˜
b = S
−1
b, ˜c = S
∗
c. Положим ξ = (ξ
1
, ξ
2
)
∗
, где ξ
1
и ξ
2
— векторы размерностей n
1
и n
2
соответственно (n
1
+ n
2
= n). Тогда
первое уравнение системы (35), примет вид (см. (10), (11))
(
˙
ξ
1
= A
11
ξ
1
+ A
12
ξ
2
+ b
1
u,
˙
ξ
2
= A
22
ξ
2
.
или
(
˙
ξ
1
= A
11
ξ
1
˙
ξ
2
= A
21
ξ
1
+ A
22
ξ
2
+ b
2
u.
(36)

55
Из (36) видим, что ξ
2
= ξ
2
(t) или ξ
1
= ξ
1
(t) не зависит от управле-
ния u = u(t). Поэтому за счет выбора управления u(t) на интерва-
ле (t
0
, t
1
) невозможно удовлетворить соответствующее решение ξ(t)
условию ξ(t
1
) = ξ
1
при произвольном ξ
1
∈ R
n
. Следовательно, пара
(
˜
A,
˜
b), значит, и пара (A, b) неполностью управляема.
9.2. Пусть имеет место утверждение ( п.упр.) — пара (A, b) непол-
ностью управляема. Тогда по доказанному выше (см. п.6, п.7)
( п.упр.)
(п.7)
⇒ (V
y
)
(п.6)
⇒ (I
y
),
и, следовательно, линейная оболочка L, натянутая на столбцы мат-
рицы R = (b, Ab, . . . , A
n−1
b) (см.(2)) не совпадает со всем простран-
ством R
n
. Так как по теореме Гамильтона-Кэли матрица A
n
являет-
ся линейной комбинацией матриц I
n
, A, . . . , A
n−1
(см. (22)), то ли-
нейное подпространство L ⊂ R
n
инвариантно относительно A. В
самом деле, пусть b
j
∈ R
n
(j = 1, . . . , m) — столбцы матрицы b:
b = (b
1
, b
2
, . . . , b
m
), и пусть x ∈ L. Тогда по самому определению L
имеем
x =
n−1
X
k=0
m
X
j=1
α
kj
A
k
b
j
, α
kj
∈ R.
Применяя к обеим частям последнего равенства оператор A, и за-
меняя матрицу A
n
ее выражением из (22) — линейной комбинацией
матриц I
n
, A, . . . , A
n−1
– получаем, что вектор
Ax =
n−1
X
k=0
m
X
j=1
α
kj
A
k+1
b
j
(α
kj
∈ R)
тоже является линейной комбинацией векторов матрицы R, т.е.
Ax ∈ L.
Обозначим через n
1
размерность линейного пространства L, а че-
рез n
2
— размерность прямого дополнения L пространства L до R
n
,
т.е. R
n
= L⊕ L (n
1
+ n
2
= n). Пусть
s
1
, s
2
, . . . , s
n
1
и
s
n
1
+1
, s
n
1
+2
, . . . , s
n
соответственно базисы в L и L. Образуем матрицы
S
1
= (s
1
, s
2
, . . . , s
n
1
) и S
2
= (s
n
1
+1
s
n
1
+2
, . . . , s
n
), столбцами которых

56
являются векторы базисов {s
j
}
n
1
j=1
и {s
j
}
n
j=n
1
+1
пространств L и L
соответственно. Положим
S = (S
1
, S
2
).
Тогда столбцы матрицы S, очевидно, образуют базис во всем про-
странстве R
n
. Стало быть, S — неособая матрица.
Так как подпространство L инвариантно относительно A, то
As
j
∈ L (j = 1, . . . , n
1
), и, поэтому,
As
j
= α
1j
s
1
+ . . . + α
n
1
j
s
n
1
(j = 1, . . . , n
1
), (37)
где α
ij
∈ R (i = 1, 2, . . . , n
1
). Равенство (37) можно записать в виде
следующего матричного равенства
AS
1
= S
1
A
11
, (38)
где A
11
— (n
1
× n
1
)-матрица, j-й столбец которой состоит из чисел
α
1j
, . . . , α
n
1
j
.
Рассмотрим теперь As
j
, где j = n
1
+ 1, . . . , n. Так как векторы
{s
j
}, (j = 1, . . . , n
1
; n
1
+ 1, . . . , n) (столбцы матрицы S) образуют
базис в R
n
, то имеют место разложения
As
j
= β
1j
s
1
+ . . . + β
n
1
j
s
n
1
+ γ
n
1
+1j
s
n
1
+1
+ . . . + γ
nj
s
n
(j = n
1
+ 1, . . . , n).
(39)
Равенства (39) можно записать в виде одного матричного равенства
AS
2
= S
1
A
12
+ S
2
A
22
, (40)
где A
12
— некоторая (n
1
×n
2
)-матрица, j-й столбец которой состоит
из чисел β
1j
, . . . , β
n
1
j
, а A
22
— тоже некоторая (n
2
× n
2
)-матрица с
j-м столбцом, состоящим из чисел γ
n
1
+1j
, . . . , γ
nj
.
По определению L столбцы матрицы b принадлежат L, следова-
тельно
b
j
= δ
1j
s
1
+ . . . + δ
n
1
j
s
n
1
(j = 1, 2, . . . , m), (41)
где δ
ij
∈ R (i = 1, . . . , n
1
).
Равенства (41) эквивалентны матричному равенству
b = S
1
b
1
, (42)
где b
1
— некоторая (n
1
×m)-матрица, j-й столбец которой образован
из чисел δ
1j
, . . . , δ
n
1
j
.

57
Матричные равенства (38), (40), (42) можно записать, очевидно, в
виде
AS = S
µ
A
11
A
12
0 A
22
¶
, S
µ
b
1
0
¶
= b.
Отсюда следует, что матрицы S
−1
AS и S
−1
b имеют вид (10). Таким
образом, (п.упр) ⇒ ( V III
y
).
10. Эквивалентность (п.упр) ⇐⇒ (V I
y
).
10.1. Пусть имеет место свойство (V I
y
), т.е. существуют ненулевой
вектор z
0
∈ C
n
и число p
0
∈ C такие, что
A
∗
z
0
= p
0
z
0
, z
∗
0
b = 0. (43)
Для произвольного комплексного числа p, отличного от собственных
значений матрицы A, используя (43), получаем
z
∗
0
(A − pI) = z
∗
0
(p
∗
0
− p). (44)
Из очевидного равенства
z
∗
0
(A − pI)(A − pI)
−1
= z
∗
0
,
с учетом (44), имеем
z
∗
0
(A − pI)
−1
= z
∗
0
(p
∗
0
− p)
−1
.
Умножая последнее равенство справа на b и используя второе равен-
ство из (43), получим
z
∗
0
(A − pI)
−1
= 0,
т.е. имеет место свойство (III
y
). Следовательно (см. выше п.5 и п.4),
(III
y
) ⇒ (II
y
) ⇒ (п.упр),
т.е. пара (A, b) неполностью управляема.
10.2. Пусть система не является полностью управляемой. Тогда в
силу вышедоказанного (см. п.9) имеет место свойство (V III
y
), т.е.
существует такая неособая матрица S, что матрицы
˜
A = S
−1
AS и
˜
b = S
−1
b
имеют вид (10) или (11). Пусть, для определенности, они имеют вид
(10) (когда
˜
A и
˜
b имеют вид (11), рассуждения аналогичны).

58
Пусть p
0
∈ C — какое-либо собственное значение матрицы A
∗
22
, а
z
0
2
6= 0 — соответствующий ему собственный вектор:
A
∗
22
z
0
2
= p
0
z
0
2
(z
0
2
∈ C
n
2
).
Тогда для вектора ˜z
0
= (0, z
0
2
)
∗
∈ R
n
имеем
e
A
∗
˜z
0
=
µ
0
A
∗
22
z
0
2
¶
=
µ
0
p
0
z
0
2
¶
= p
0
˜z
0
;
e
b
∗
˜z
0
= 0.
Так как
e
A
∗
= S
∗
A
∗
(S
∗
)
−1
,
e
b
∗
= b
∗
(S
∗
)
−1
,
то
A
∗
(S
∗
)
−1
˜z
0
= p
0
(S
∗
)
−1
˜z
0
, b
∗
(S
∗
)
−1
˜z
0
= 0.
Последние равенства означают, что
A
∗
z
0
= p
0
z
0
, b
∗
z
0
= 0,
где z
0
= (S
∗
)
−1
˜z
0
, причем z
0
6= 0 в силу того, что S — неособая
матрица, т.е. свойство (V I
y
) выполнено.
Таким образом, мы показали, что полная управляемость пары
(A, b) равносильна выполнению свойства (V I
y
).
11. Эквивалентность (III
y
) ⇐⇒ (IV
y
).
11.1. Пусть справедливо (IV
y
), т.е.
rank (d
0
, . . . , d
n−1
) < n, (45)
где d
0
, . . . , d
n−1
— коэффициенты многочлена (8). Из неравенства
(45) следует, что существует ненулевой вектор z
0
∈ R
n
такой, что
z
∗
0
d
0
= 0, . . . , z
∗
0
d
n−1
= 0. (46)
Умножая обе части равенства (8) слева на z
∗
0
и учитывая (46), полу-
чим
z
∗
0
(pI − A)
−1
b = 0
для всех p, отличных от собственных значений матрицы A, т.е. вы-
полнено свойство (III
y
) (за множество Ω можно принять множество
C\{λ
j
(A)}, где λ
j
(A) — собственные числа матрицы A).
11.2. Пусть выполнено (III
y
), т.е. существует такой ненулевой век-
тор z
0
∈ C
n
, что имеет место равенство (7). Тогда из равенства (8)
получаем, что
z
∗
0
d
n−1
p
n−1
+ . . . + z
∗
d
0
= 0 ∀p ∈ Ω, (47)

59
где Ω ⊂ C — множество, фигурирующее в (III
y
) теоремы 1.
Очевидно, что из (47) следуют равенства (46), которые означают
выполнение свойства (IV
y
).
Таким образом, нами доказана цепочка импликаций (13) и, значит,
имеем место (12). Тем самым, теорема 1 доказана полностью.
Из теоремы 1 вытекают следующие следствия.
Следствие 1. Пусть пара (A, b) полностью управляема. Тогда
для любой (n × m)-матрицы s пара (A + bs
∗
, b) также полностью
управляема.
Действительно, по доказанной выше теореме полная управляе-
мость равносильна свойству (IV
y
). Поэтому, предполагая, что вы-
полнены равенства
(A + bs
∗
)
∗
z = pz, b
∗
z = 0
для какого-либо p ∈ C и z ∈ C
n
, будем иметь:
A
∗
z = pz, b
∗
z = 0.
Отсюда, используя свойство (V I
y
), получим, что z = 0. Следователь-
но, пара (A + bs
∗
, b) полностью управляема.
Следствие 2. Если пара (A, b) полностью управляема, то пол-
ностью управляема также и пара (
e
A,
e
b), где
e
A = S
−1
AS,
e
b = S
−1
b
(S — произвольная вещественная неособая матрица).
Д о к а з а т е л ь с т в о. Составим матрицу
e
R = (
e
b,
e
A
e
b, ··· ,
e
A
n−1
e
b).
Легко видеть, что
e
R = S
−1
R,
где R — матрица (3). Поскольку при умножении матрицы на неосо-
бую матрицу ее ранг не изменяется, то
rank
e
R = rank R.
Отсюда, в силу полной управляемости пары (A, b), согласно свойству
(I
y
) теоремы будем иметь
rank
e
R = n.
Следовательно, в силу того же свойства (I
y
) пара (
e
A,
e
b) полностью
управляема.

60
Следствие 3. Если пара (A, b) полностью управляема, и λ
0
—
произвольное собственное число матрицы A, то дефект (разность
между порядком матрицы и ее рангом) d матрицы (A − λ
0
I) не
превосходит ранга матрицы b.
В частности, если m = 1, то d = 1.
Действительно, пусть r — ранг матрицы b. Предположим, что
d > r. Поскольку при умножении матрицы на неособую матрицу
ее ранг не изменяется, то
rank (A − λ
0
I) = rank J,
где J = S
−1
(A−λ
0
I)S — каноническая (жорданова) форма матрицы
(A − λ
0
I), S — некоторая неособая матрица.
Так как число линейно независимых столбцов у матрицы b равно
r, а у матрицы J (и значит, у матрицы (A−λ
0
I)) равно n−d, то число
линейно независимых столбцов матрицы (A −λ
0
I, b) не превосходит
r + n − d, т.е.
rank (A − λ
0
I, b) ≤ r + n − d. (48)
Поскольку r + n −d < n, то из (48) следует, что выполнено свойство
(V II
y
), равносильное неуправляемости пары (A, b), что противоре-
чит условию. Следовательно, d ≤ r, что и утверждалось.
Замечание 1. Так как, очевидно, дефект матрицы A −λ
0
I равен
числу жордановых клеток в канонической форме матрицы A, отве-
чающих собственному значению λ
0
, то в случае m = 1, т.е. когда b
— одностолбцовый вектор, из полной управляемости пары (A, b) (в
силу следствия 3) следует, что каждому собственному значению λ
0
матрицы A отвечает лишь одна жорданова клетка в канонической
форме матрицы A.
Замечание 2. Из свойства (V III
y
) вытекает, к какому виду (36)
может быть приведена система, если она неполностью управляема.
Из (36) видно, что в неполностью управляемой системе всегда мо-
жет быть выделена подсистема, в которой отсутствует управляющее
воздействие.
