Леонов Г.А., Шумафов М.М. Проблемы стабилизации линейных управляемых систем

Подождите немного. Документ загружается.

141

Теорема 2 (о стабилизируемости тройки (A, b, c)).Пусть мат-

рицы A, b и c в системе (1) удовлетворяют следующим условиям:

1) пара (A, b) стабилизируема, а пара (A, c) полностью наблюда-

ема;

2) существуют вещественные соответственно (`×m)- и (m×n)-

матрицы s и g, удовлетворяющие соотношениям (23), (24), где H =

∗

— вещественная положительно определенная матрица.

Тогда система (1) стабилизируема.

Д о к а з а т е л ь с т в о . Из соотношений (23) и (24), оче-

видно, следует, что выполнено равенство (25). Отсюда, поскольку

css

∗

≥ 0, получаем неравенство

(A + bs

∗

)

∗

H + H(A + bs

∗

) ≤ −cc

∗

. (26)

Так как пара (A, c) полностью наблюдаема, то по теореме двой-

ственности Калмана пара (A

∗

, c) и, следовательно, в силу следствия 1

теоремы о критериях управляемости (см. § 1, гл.II) пара

∗

+ csb

∗

, c) будет полностью управляемой. Поэтому по той же тео-

реме двойственности Калмана полностью наблюдаемой будет пара

(A + bs

∗

, c). Отсюда и из неравенства (26) в силу леммы 2 следует,

что A + bs

∗

гурвицева, так как H > 0. Последнее означает, что

тройка (A, b, c) стабилизируема. Теорема 2 доказана.

Замечание 1. Условия теоремы 2 являются лишь достаточными,

но не необходимыми. В работе [237] показано, что условия теоре-

мы 1 являются и достаточными для стабилизируемости системы (1).

Как это видно из сравнений условий теорем 1 и 2, условия теоре-

мы 2 несколько более стеснительны, чем условия теоремы 1: вместо

стабилизируемости пары (A

∗

, c) и неотрицательной определенности

матрицы H (в теореме 1) требуется соответственно полная наблюда-

емость пары (A, c) и положительная определенность матрицы H (в

теореме 2).

Замечание 2. Левая часть равенства (25) определяет, очевидно,

линейный оператор K в (линейном) пространстве эрмитовых матриц

{H} (H

∗

= H):

K(H) = (A + bs

∗

)

∗

H + H(A + bs

∗

В силу леммы 1 (леммы А.М.Ляпунова) уравнение K(H) = G од-

нозначно разрешимо при любой матрице G = G

∗

, поскольку A+bs

∗

142

— гурвицева матрица. Поэтому оператор K обратим. Обозначим че-

рез L — линейный оператор, обратный к K : L = K

−1

. Тогда реше-

ние H уравнения (25) можно записать так: H = −L(cc

∗

) −L(css

∗

Подставляя это значение H в уравнение (23) (предварительно сделав

операцию транспонирования в обеих его частях) получим квадрат-

ное уравнение относительно (` × m)-матрицы (cs):

L(css

∗

)b − cs = −g

∗

− L(cc

∗

)b.

(В таком виде записывались так называемые разрешающие урав-

нения Лурье в векторной форме [3,49,102,103,105]). Таким образом,

уравнения (25), (23), а значит, и уравнения (24), (23) сводятся к урав-

нениям Лурье-Риккати. Очевидно, верно и обратное. В [105] и др.

были получены условия разрешимости уравнений Лурье в случаях

m = 1, ` = 2, 3, 4, 5. С использованием этих уравнений были найде-

ны решения многих практически важных задач. Для общего случая

условием разрешимости уравнений Лурье является так называемое

"частотное"условие Якубовича-Калмана [54], которое в случае ли-

нейных систем вида (1) совпадает с критерием Найквиста.

Замечание 3. Проблема стационарной стабилизации линейных

систем вида (1) является одной из самых важных вопросов в теории

управления при синтезе линейной обратной связи, поскольку одним

из достоинств решения этой проблемы является его аналитически

замкнутая форма. Поэтому этой проблеме посвящено большое ко-

личество работ, обзор которых можно найти, например, в статьях

[196,282] .

§ 8. Стабилизируемость неполностью управляемых систем

В § 4 настоящей главы мы доказали теорему о стабилизации пары

(A, b) в предположении её полной управляемости. Приведем теперь

теорему, дающую достаточное условие стабилизируемости системы

˙x = Ax + bu, x ∈ R

, u ∈ R

(1)

(где A и b — постоянные (n ×n)- и (n ×m)-матрицы соответственно)

в случае, когда пара (A, b) не является полностью управляемой.

Пусть среди n корней λ

, ··· , λ

(каждый корень выписывается

столько раз, какова его кратность) характеристического уравнения

143

det (pI − A) = 0 имеются ровно k таких, у которых вещественные

части неотрицательны (а у остальных n−k корней— отрицательны).

Тогда систему (1) невырожденным линейным преобразованием пе-

ременных x = Qy (y ∈ R

, Q — неособая матрица) можно привести

к виду (за матрицу Q достаточно взять матрицу, приводящую A к

вещественной жордановой нормальной форме):

(

˙y

u, y

∈ R

˙y

u, y

∈ R

n−k

, u ∈ R

)

где

A ≡

= Q

−1

AQ,

b ≡

, (3)

причем

∈ R

n−k

— (k × k)-матрица, все собственные

числа которой имеют неотрицательные вещественные части, а

—

гурвицева матрица порядка (n − k) × (n − k);

— матрицы

порядков k × m и (n − k) × m соответственно.

Теорема (о стабилизируемости неполностью управляемой

системы). Пусть в системе (2

), (2

)

rank (

, ··· ,

k−1

) = k < n.

Тогда система (1) стабилизируема.

Д о к а з а т е л ь с т в о . По теореме о стабилизации из § 5,

примененной к подсистеме (2

) системы (2

),(2

) существует (веще-

ственная) (k×m)-матрица es

такая, что матрица

∗

гурвицева,

а u = es

∗

есть стабилизирующее управление для подсистемы (2

При таком управлении матрица (полной) системы (2

), (2

) имеет

вид

B =







∗

| 0

∗

| A







n-k

| {z }

|{z}

n-k

(4)

144

Характеристический многочлен этой матрицы по теореме Лапласа

о разложении определителя по k строкам можно записать так:

det (pI −B) = det [pI −(

∗

)] · det (pI −

Так как матрицы

∗

гурвицевы, то в силу последнего

равенства и матрица B тоже будет гурвицевой.

Таким образом, управление

u = es

∗

где

∗

= ( es

∗

|{z}

, 0

|{z}

n−k

) (5)

(es

∗

— матрица, полученная из матрицы es

∗

дополнением её до (m×n)-

матрицы нулевой матрицей порядка m × (n − k) является стабили-

зирующей для всей системы (2

),(2

)).

Чтобы построить стабилизирующее управление для исходной си-

стемы (1), перепишем матрицу (4) так:

B =

A +

bes

∗

. (6)

С учетом равенств (3), представим матрицу (6) в виде

B = Q

−1

AQ + Q

−1

bes

∗

= Q

−1

(A + bes

∗

−1

)Q. (7)

Поскольку матрица B гурвицева и, в силу (7), матрицы B и

C = A + bs

∗

где

s = (Q

∗

)

−1

, (8)

подобны, то матрица C тоже гурвицева (es

∗

— матрица (5)). Послед-

нее означает, что пара (A, b) стабилизируема, причем стабилизирую-

щее управление имеет вид

u = s

∗

где s — матрица (8).

145

ГЛАВА IV

НЕСТАЦИОНАРНАЯ НИЗКОЧАСТОТНАЯ

СТАБИЛИЗАЦИЯ ЛИНЕЙНЫХ СИСТЕМ

В следующих двух главах мы будем рассматривать задачу неста-

ционарной линейной стабилизации (соответственно низкочастотной

и высокочастотной).

§ 1. Постановка задачи. Проблема Брокетта

Рассмотрим линейную систему

˙x = Ax + bu, y = c

∗

x, x ∈ R

, u ∈ R

, y ∈ R

, (1)

где A, b и c вещественные постоянные (n × n)−, (n × m)− и (n ×

`)-матрицы соответственно. Р.Брокетт в книге [198] сформулировал

следующую задачу: найти (`×m)-матрицу s(t) такую, чтобы система

(1), замкнутая обратной связью

u = s(t)

∗

y, (2)

была асимптотически устойчивой (в целом).

Другими словами, проблема Брокетта формулируется так: дана

тройка матриц A, b и c (порядков n × n, n × m и n × ` соответ-

ственно). Спрашивается при каких условиях существует матрица

s(t) (порядка (` × m)) такая, что система

˙x = (A + bs(t)

∗

)x (x ∈ R

) (3)

является асимптотически устойчивой ?

В предыдущей главе нами была рассмотрена задача стабилизации

системы (1) с помощью постоянной матрицы s(t) ≡ s = const . В

проблеме Брокетта требуется найти переменную стабилизирующую

матрицу s = s(t), обладающую указанным выше свойством. Поэтому

проблему Брокетта можно переформулировать следующим образом.

Насколько введение зависимых от времени t матриц s(t) расши-

ряет возможности стационарной стабилизации ?

В задачах стабилизации механических систем часто оказывает-

ся необходимым рассматривать более узкий класс стабилизирующих

146

матриц s(t), а именно, периодические матрицы s(t), имеющие нуле-

вое среднее на периоде [0, T ]:

s(t) dt = 0. (4)

В настоящей главе рассматриваются алгоритмы построения пе-

риодических кусочно-постоянных функций s(t), решающих в ряде

случаев проблему Брокетта. При изложении соответствующих ре-

зультатов будем следовать работам [96,98,245–247].

§ 2. Линейные системы дифференциальных уравнений

с периодической матрицей

Напомним основные факты из теории линейных уравнений с пе-

риодическими коэффициентами, которые нам понадобятся в даль-

нейшем.

1. Фазовые потоки. Понятие фазового потока и фазового про-

странства являются основными в теории дифференциальных урав-

нений.

Рассмотрим линейную систему

˙x = A(t)x, t ∈ R, x ∈ R

(1)

с кусочно-непрерывной на R периодической с периодом T > 0 мат-

рицей A(t):

A(t + T ) = A(t) ∀t ∈ R.

Пространство R

называется фазовым пространством, а прямое

произведение R

n+1

= R × R

— расширенным фазовым простран-

ством системы (1).

Пример. Уравнение маятника (при малых колебаниях и отсут-

ствии трения) имеет вид

¨x + ω

x = 0.

Частота ω определяется длиной маятника ` : ω =

(g — уско-

рение свободного падения). Колебания маятника переменной длины

описываются аналогичным уравнением:

¨x + ω

(t)x = 0,

147

которое можно записать в виде системы (1):

˙x = x

˙x

= −ω

(t)x

, A(t) =

0 1

−ω

(t) 0

(Примером маятника переменной длины являются качели.)

В случае, когда в (1) матрица A(t) непрерывна, из общего курса

дифференциальных уравнений известно, что решение x = ψ(t; x

, t

)

уравнения (1) существует, определяется начальным условием

ψ(t

; x

, t

) = x

однозначно и зависит от t

, x

и t непрерывно, при-

чем все решения уравнения (1) неограниченно продолжаемы вправо

и влево, т.е. определены на всей оси (−∞, +∞). В случае, когда A(t)

кусочно-непрерывна, а матрица-функция A(t) имеет точки разрыва

первого рода (скачки), всю ось (−∞, +∞) можно разбить на счет-

ное число интервалов I

= (t

k−1

, t

) (k = 1, 2, ···), на каждом из

которых матрица A(t) непрерывна и, следовательно, решения урав-

нения (1) определены на интервалах I

(k = 1, 2, . . .). Далее, в точ-

ках разрыва t

, разделяющих интервалы непрерывности I

, решения

"склеиваются". А именно, пусть решение x = ψ

(t) определено на

= (t

k−1

, t

). Тогда чтобы продолжить это решение на следующий

интервал I

k+1

= (t

, t

k+1

), достаточно продолжить сначала реше-

ние ψ

(t) до точки t = t

, затем взять на интервале I

k+1

то реше-

ние x = ψ

k+1

(t), которое удовлетворяет условию: ψ

k+1

) = ψ

Продолжая этот процесс вправо и, аналогично, влево, получим ре-

шение x = ψ(t) уравнения (1), определенное и непрерывное на всей

оси (−∞, +∞). Причем это решение обладает теми же свойствами

(единственности, непрерывной зависимости от начальных условий),

что и в случае непрерывной матрицы A(t) (см.[155,214]).

График решения x = ψ(t) системы (1) называется интегральной

кривой, а образ отображения ψ : R → R

— фазовой кривой или

траекторией системы (1).

Таким образом, траектория системы (1) лежит в фазовом про-

странстве R

, а интегральная кривая — в расширенном фазовом

пространстве R

n+1

Пусть x = ψ(t; x

, t

) (t ∈ R) — решение системы (1) с начальным

условием

ψ(t

; x

, t

) = x

∈ R; x

∈ R

). (2)

148

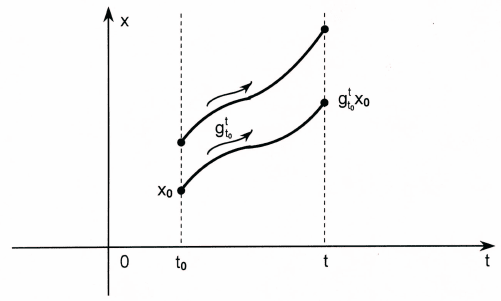
О п р е д е л е н и е 1. Преобразованием за время от t

до t, осу-

ществляемым траекториями системы (1), называется отображе-

ние фазового пространства R

в себя, сопоставляющее начальному

условию x

в момент t

значение решения x = ψ(t; x

, t

) системы

(1) в момент t (рис.10).

Это преобразование обозначается так: g

Таким образом,

: R

→ R

: g

= ψ(t; x

, t

) ∀x

∈ R

, t ∈ R) (3)

Рис.11. Преобразование g

за время от t

до t.

Из формулы (3) следует, что, если отождествить каждую гипер-

плоскость t = t

в расширенном фазовом пространстве с фазовым

пространством R

, то преобразование g

, t

∈ R) можно рассмат-

ривать как отображение (осуществляемое интегральными кривыми

системы (1)) гиперплоскости t = t

в гиперплоскость t = t

О п р е д е л е н и е 2. Семейство преобразований {g

∈ R, t ∈ R} называется ф а з о в ы м п о т о к о м системы (1) с

фазовым пространством R

Траектории системы (1) называются траекториями соответству-

ющего ей фазового потока.

Замечание. В частном случае, когда в системе (1) матрица A(t)

постоянная: A(t) ≡ A (A = const ), преобразования g

зависят лишь

149

от разности t − t

и совпадают с преобразованием g

t−t

за время от

0 до t − t

= g

t−t

(∀t

, t ∈ R

). (4)

Последнее равенство следует из теоремы единственности решений

и того факта, что если x = ψ(t) — решение системы ˙x = Ax (A =

const ) с начальным условием ψ(t

) = x

, то x = ψ

(t) ≡ ψ(t + t

)

— решение этой системы с начальным условием ψ

(0) = x

(сдвиг

решения вдоль оси t есть снова решение — свойство, которым об-

ладают все решения систем дифференциальных уравнений, правые

части которых не зависят от t (автономные системы)). Поэтому для

системы ˙x = Ax (x ∈ R

) с постоянной матрицей A, в силу (4), мож-

но говорить о преобразовании за время τ = t−t

или (переобозначив

τ → t ) за время t. Преобразование за время t, соответствующее си-

стеме (1) с постоянной матрицей A(t) ≡ A, будем обозначать через

(без нижнего индекса 0), т.е.

:= g

(∀t ∈ R), (5)

и соответственно ее фазовый поток — {g

, t ∈ R} или просто {g

2. Примеры фазовых потоков простейших дифференци-

альных уравнений.

1. ˙x = 0. Фазовый поток есть g

x = x (x ∈ R).

2. ˙x = 1. Фазовый поток — g

x = x + t (x ∈ R).

3. ˙x = kx. Имеем x(t) = e

. Поэтому фазовый поток есть

}; g

x = e

x(∀ x ∈ R).

4. ˙x = y, ˙y = 0. Решение этой системы: x(t) = x

+ ty

, y(t) = y

Поэтому фазовый поток — g

: (x, y) → (x + ty, y) ∀(x, y) ∈ R

5. ˙x = y, ˙y = 1. Решение: x(t) = x

+ y

t + t

/2, y(t) = y

+ t.

Фазовый поток – g

: (x, y) → (x + ty + t

/2, y + t) ∀(x, y) ∈ R

6. ˙x = y, ˙y = −x (уравнения малых колебаний маятника). Реше-

ние:

x(t) = x

cos t + y

sin t,

y(t) = −x

sin t + y

cos t.

Фазовым потоком являются повороты плоскости (x, y) на угол t

(эллиптические повороты):

cos t sin t

−sin t cos t

150

(Здесь отображение g

отождествляется с матрицей, описывающей

его в базисе e

= (1, 0)

∗

, e

= (0, 1)

∗

). Для любой точки (x, y) ∈ R

: (x, y) → (x cos t + y sin t, −x sin t + y cos t).

Траекториями фазового потока являются окружности (аффинные

образы эллипсов) — под действием фазового потока точки плоскости

движутся по окружностям.

7. ˙x = y, ˙y = x (уравнение малых колебаний перевернутого маят-

ника). Решение:











x(t) = x

+ e

−t

+ y

− e

−t

= x

ch t + y

sh t,

y(t) = x

− e

−t

+ y

+ e

−t

= x

sh t + y

ch t.

Здесь фазовым потоком являются гиперболические повороты:

ch t sh t

sh t ch t

(отображение g

отождествляется с описывающей его матрицей в ба-

зисе e

= (1, 0)

∗

, e

= (0, 1)

∗

). Для любой точки (x, y) ∈ R

: (x, y) → (xch t + ysh t, xsh t + ych t).

Траекториями фазового потока являются гиперболы — под действи-

ем фазового потока точки плоскости движутся по гиперболам.

Преобразование g

(гиперболический поворот) состоит из сжатия

в e

раз в направлении собственного вектора ξ

, соответствующего

собственному значению λ

= −1 матрицы g

, и растяжения в e

раз

в направлении собственного вектора ξ

, соответствующего собствен-

ному значению λ

= 1.

Заметим, что эллиптический и гиперболический повороты сохра-

няют площади (так как det g

= 1).

Замечание . В вышеприведенных примерах гладкое векторное

поле, заданное дифференциальным уравнением (или системой), опре-

деляло фазовый поток. Возникает вопрос, всякое ли гладкое вектор-

ное поле определяет фазовый поток ? Ответ — нет, не всякое.

Контрпримером может служить уравнение: ˙x = x

, x ∈ R. Реше-

ние этого уравнения: x(t) = x

/(1 − x

t). Поэтому g

x = x/(1 − xt).

Однако последняя формула не задает фазовый поток – отображение