Леонов Г.А., Шумафов М.М. Проблемы стабилизации линейных управляемых систем

Подождите немного. Документ загружается.

181

Для доказательства теоремы 2 достаточно определить функцию

s(t) следующим образом:

s(t) =







при t ∈ [0, |σ

/2s

|),

при t ∈ [|σ

/2s

|, τ

+ |σ

/2s

|), s(t + T ) = s(t),

при t ∈ [τ

+ |σ

/2s

|, τ

+ |σ

|),

(20)

где T : = τ

(1 −σ

) — период функции s(t). Здесь τ

— достаточно

большое число, удовлетворяющее условию (19). Легко проверить, что

функция s(t) имеет нулевое среднее на периоде. Далее, доказатель-

ство теоремы 2 полностью повторяет рассуждения доказательства

теоремы 1. При этом

= t

:= −σ

/2s

, τ := τ

Замечание 1. Условие ограниченности функции kθ

k на [0, +∞)

можно заменить следующим условием: все собственные значения λ

матрицы A + b(cσ

)

∗

обладают неположительными вещественными

частями:

Re λ

(A + b(cσ

)

∗

) ≤ 0 (k = 1, . . . , n),

причем собственные числа, имеющие нулевые вещественные части,

допускают лишь простые элементарные делители т.е. соответствую-

щие клетки в жордановой нормальной форме матрицы сводятся к

одному элементу.

Замечание 2. Теорема из § 3 является следствием теоремы 2.

Действительно, применим теорему 2 к системе (4) из § 3 с функци-

ей s(t) вида (5) в предположении, что выполнено условие α

< 4

(β −ν

) (не умаляя общности будем считать, что β −ν

−α

/4 = 1 ).

Тогда характеристический многочлен системы (4) из § 3 с s(t) = σ

где σ

= β, имеет комплексно-сопряженные корни и, следовательно,

выполнено условие (19) с некоторым τ

> 0 ({θ

} — фазовый поток

системы (7) из § 3). Поэтому τ

:= τ

+ 2πj, j ∈ Z. Легко видеть,

что функция kθ

k ограничена на [0, +∞), так как преобразование θ

аффинно эквивалентно повороту на угол t с последующим сжатием.

Далее, при s(t) = s

, где s

:= −β, характеристический многочлен

системы (4)(§ 3) имеет вещественные корни −λ < 0 и κ > 0, причем

λ > κ.

182

Таким образом, выполнены все условия теоремы 2 и, следователь-

но, система (4) (из § 3) с функцией s(t) вида (20) асимптотически

устойчива (при этом T = 2τ

§ 5. Некоторые предложения, обеспечивающие

эффективную проверку "условия вложения многообразий"

Рассмотрим систему

˙z = Qz, z ∈ R

, (1)

где Q — постоянная неособая (n × n)–матрица.

Пусть h ∈ R

— произвольный ненулевой вектор.

Лемма 1. Предположим, что решение z(t) системы (1) имеет

вид

z(t) = v(t) + w(t), t ∈ [0, +∞),

где v(t) — периодическая вектор-функция такая, что h

∗

v(t) 6≡ 0, w(t)

— вектор-функция, для которой

+∞

kw(τ)kdτ < +∞, lim

t→+∞

w(t) = 0.

Тогда существуют числа τ

и τ

такие, что выполнены неравенства

∗

z(τ

) > 0, h

∗

z(τ

) < 0, (2)

т.е. функция h

∗

z(t) меняет свой знак (рис.18).

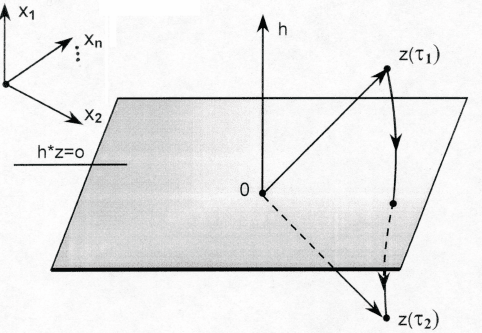
183

Рис. 18. Переход решения z(t) с одной стороны плоскости h

∗

z = 0

на другую.

Д о к а з а т е л ь с т в о . Предположим противное, т.е. что

∗

z(t) ≥ 0 ∀t ≥ 0 или h

∗

z(t) ≤ 0 ∀t ≥ 0. Пусть, для определенности,

∗

z(t) ≥ 0 ∀t ≥ 0. Тогда и h

∗

v(t) ≥ ∀t ≥ 0. Действительно, в про-

тивном случае существует момент t

такой, что h

∗

v(t

) < 0 и в силу

периодичности h

∗

v(t) будем иметь

∗

z(t

+ nT ) = h

∗

v(t

) + h

∗

w(t

+ nT ) < 0

для достаточно больших n ∈ N (здесь T — период функции v(t)).

Отсюда, в силу условия h

∗

v(t) 6≡ 0, следует, что

+∞

∗

v(τ)dτ = +∞,

так как h

∗

v(t) — периодическая функция.

Поэтому будет выполнено также соотношение

lim

t→+∞

∗

z(τ )dτ = +∞. (3)

184

С другой стороны

∗

z(τ )dτ =

∗

−1

˙z(τ )dτ = h

∗

−1

(z(t) − z(0)).

Отсюда и из ограниченности функции z(t) на [0, +∞) следует огра-

ниченность функции

∗

z(τ )dτ.

Последнее противоречит соотношению (3). Полученное противоре-

чие доказывает лемму 1.

Следствие. Пусть решение z(t) системы ˙z = P z с постоянной

(не обязательно неособой) (n × n)–матрицей P имеет вид

z(t) = e

λt

[v(t) + w(t)],

где число λ не является собственным значением матрицы P, а v(t)

и w(t) удовлетворяют условиям леммы 1. Тогда справедливо утвер-

ждение леммы 1, т.е. имеют место неравенства (2).

Для доказательства следствия достаточно заметить, что функ-

ция ζ(t) = e

−λt

z(t) является решением уравнения

ζ = (P − λI)ζ

(где I — единичная матрица) и, тогда остается применить лемму 1

к последнему уравнению, полагая Q := P − λI.

Лемма 2. Пусть n = 2 и матрица Q в (1) имеет комплексно-

сопряженные собственные значения α ± iβ.

Тогда для любой пары ненулевых векторов h ∈ R

и d ∈ R

суще-

ствуют числа τ

и τ

такие, что

∗

Qτ

d > 0, h

∗

Qτ

d < 0, (4)

т.е. решениеz(t) = e

d системы (1) попадает на плоскость

∗

z} = 0 в некоторый момент τ ∈ (τ

, τ

Д о к а з а т е л ь с т в о . В рассматриваемом случае фазовый

поток {g

} системы (1) аффинно эквивалентен семейству растяже-

ний (если α < 0, то вместо растяжений имеем сжатия) в e

αt

раз с

одновременным вращением на угол β.

185

Поэтому, очевидно, для любого вектора d ∈ R

существуют такие

числа τ

и τ

, что

∗

d > 0, h

∗

d < 0.

Так как

z(t; d) = e

d, d ∈ R

— решение системы (1) с начальным условием z(0; d) = d, то

(см. п.1,§ 2)

= e

Следовательно, имеют место неравенства (4). Лемма 2 доказана.

Следующая лемма является обобщением леммы 2.

Лемма 3. Пусть матрица Q имеет пару комплексно-сопряжен-

ных собственных чисел α ± iβ кратности 1, а остальные ее соб-

ственные числа λ

(Q) удовлетворяют условию Re λ

(Q) < α (j =

1, ··· , n − 2).

Пусть, далее, для векторов h ∈ R

и d ∈ R

выполнены неравен-

ства

det(d, Qd, . . . , Q

n−1

d) 6= 0, (5)

det(h, Q

∗

h, . . . , (Q

∗

)

n−1

h) 6= 0. (6)

Тогда существуют числа τ

и τ

такие, что

∗

Qτ

d > 0, h

∗

Qτ

d < 0, (7)

т.е. решение x = e

d системы (1) попадает на плоскость

∗

z = 0} в некоторый момент t = τ ∈ (τ

, τ

Напомним, что условия (5) и (6) — это условия полной управляе-

мости пары (Q, d) и полной наблюдаемости пары (Q, h).

Д о к а з а т е л ь с т в о л е м м ы 3. В силу условий леммы 3

решение

z(t) = e

системы (1) можно представить в виде

z(t) = e

αt

v(t) +

(t), (8)

186

где каждая компонента вектор-функции v(t) имеет вид c

cos βt +

sin βt (c

, c

— константы), и, поэтому, v(t) — периодическая функ-

ция; p

(t) — вектор-функция, каждая компонента которой есть неко-

торый многочлен от t (в частности, константа).

Перепишем (8) в форме

z(t) = e

αt

(v(t) + w(t)),

где

w(t) =

(λ

−α)t

(t).

Очевидно, функции v(t) и w(t) удовлетворяют условиям леммы 1.

Далее, из условий (5) (полной управляемости пары (Q, d)) и (6)

(полной наблюдаемости пары (Q, h)) следует соотношение h

∗

v(t) 6≡ 0.

Теперь, применяя следствие леммы 1, получим что справедливы

неравенства (7). Лемма 3 доказана.

Рассмотрим систему (8) из § 4 при n = 2, т.е. систему

˙x = (A + bs(t)

∗

)x, x ∈ R

, (9)

где периодическая матрица s(t) имеет вид (9) (§ 4).

Из теоремы § 4 и леммы 2 вытекает следующая

Теорема. Пусть для системы (9) существуют матрицы s

и σ

удовлетворяющие следующим условиям:

1) det bs

∗

6= 0, T r bs

∗

6= 0;

если det bs

∗

= 0, то пусть выполняется хотя бы одно из нера-

венств

det A 6= 0 или det(a

, r

) + det(r

, a

) 6= 0,

где a

, a

и r

, r

— первый и второй столбцы матриц A и bs

∗

соответственно:

A = (a

, a

), bs

∗

= (r

, r

2) матрица A + bσ

c имеет комплексно-сопряженные собствен-

ные числа.

Тогда существует периодическая матрица

(

)

такая, что си-

стема (9) асимптотически устойчива.

Д о к а з а т е л ь с т в о . Положим в формуле (9) из § 4

= s

= µs

, σ(t) ≡ σ

187

где |µ| — достаточно большое число и T r µbs

∗

< 0. Из последнего

неравенства следует, что (при достаточно большом |µ| )

T r (A + µbs

∗

) < 0. (10)

Пусть λ и κ — собственные числа матрицы A + µbs

∗

. Тогда в силу

(10) λ + κ < 0. Следовательно, одно из чисел λ, κ отрицательно,

скажем λ. Если det bs

∗

6= 0, то при достаточно большом |µ|

det(A + µbs

∗

) 6= 0.

Последнее соотношение имеет место и тогда, когда det bs

∗

= 0.

Действительно, в этом случае (по условию теоремы), как легко ви-

деть, квадратичная функция ϕ(ε) = det(bs

∗

+ εA) отлична от нуля

для всех достаточно малых ε и, значит, при достаточно большом

|µ| ϕ(1/µ) 6= 0. Следовательно, λκ 6= 0, т.е. κ 6= 0. В зависимости

от знака κ особая точка x = 0 системы (9), где s(t) ≡ s

или седло

(если κ > 0 ), или устойчивый узел (если κ < 0 ).

В любом случае система (9), где s(t) ≡ s

, имеет одномерные ин-

вариантные устойчивое многообразие L

(соответствующее собствен-

ному числу λ < 0) и ( устойчивое или неустойчивое) многообразие

(соответствующее собственному числу κ ). Поэтому для этой си-

стемы выполнены условия (3), (4) и (7) из § 4 с λ

= λ

= −λ, κ

= κ (L

≡ L

, M

≡ M

). Заметим, что если κ < 0, то система

(9) будет, очевидно, асимптотически устойчива.

В силу леммы 2 и условия 2) теоремы для системы (9), где

s(t) ≡ s

, выполнено "условие вложения многообразий"(6) из § 4.

Итак, выполнены все условия основной теоремы из § 4 и, следо-

вательно, система (9) с функцией s(t) вида (9) (§ 4), где s

= s

, σ(t) ≡ σ

, асимптотически устойчива. Теорема доказана.

188

§ 6. Стабилизация линейной системы в скалярном случае

(когда вход и выход — скалярные функции)

Рассмотрим теперь важный для теории управления случай, когда

в системе

˙x = Ax + bu, y = c

∗

x, x ∈ R

, (1)

(A — вещественная (n × n) -матрица), b и c — одностолбцовые n-

мерные векторы (вход u и выход y являются скалярными функция-

ми).

Всюду в дальнейшем будем предполагать, что передаточная функ-

ция W (p) = c

∗

(A−pI)

−1

b системы (1) невырождена. В силу теоремы

2 из § 3, гл.II, это означает, что пара (A, b) полностью управляема, а

пара (A, c) полностью наблюдаема.

Вначале докажем две леммы, устанавливающие полную наблюда-

емость и полную управляемость системы

˙x = (A + µbc

∗

)x, x ∈ R

, (2)

где µ 6= 0 — параметр, обладающий (n − 1)-мерным и одномерным

интегральными многообразиями.

Лемма 1. Если гиперплоскость {x ∈ R

: h

∗

x = 0}, где

h ∈ R

, h 6= 0 — интегральное многообразие для системы (2), то

пара (A, h) полностью наблюдаема.

Д о к а з а т е л ь с т в о . Предположим противное — пара

(A, h) неполностью наблюдаема. Тогда в силу теоремы двойственно-

сти Калмана (см.§ 3, гл.II) пара (A

∗

, h) неполностью управляема и,

следовательно, не выполнено свойство (V I

) полной управляемости

(см. § 1, гл.II ), т.е. существуют ненулевой вектор ξ ∈ C

= CR

число λ ∈ C такие, что

∗

ξ = 0, Aξ = λξ (ξ 6= 0). (3)

Из полной наблюдаемости пары (A, c) следует неравенство c

∗

ξ 6= 0.

Действительно, в противном случае мы имели бы неполностью на-

блюдаемую пару (A, c).

Так как {h

∗

x = 0} — интегральное многообразие для системы (2),

то векторное поле, определяемое системой (2), ортогонально вектору

h, т.е.

∗

(A + µbc

∗

)x = 0 ∀x ∈ {h

∗

x = 0}

189

(подпространство {h

∗

x = 0} ⊂ R

инвариантно относительно опера-

тора A + µbc

∗

). Отсюда следует, что

∗

(A + µbc

∗

)

x = 0, k = 1, 2, . . . ,

для всех x ∈ {h

∗

x = 0} ⊂ R

Из последних равенств выводим, что имеют место также соотно-

шения

∗

(A + µbc

∗

)

z = 0, k = 1, 2, . . . ,

для всех z из комплексной гиперплоскости

{z ∈ CR

: h

∗

z = 0} (z = x + iy, x, y ∈ R

При k = 1 и z = ξ, в силу (3), получим

0 = h

∗

Aξ + µh

∗

ξ = µh

∗

ξ.

Отсюда h

∗

b = 0 (так как c

∗

ξ 6= 0).

При k = 2 и z = ξ, используя (3) и предыдущее равенство, будем

иметь

0 = h

∗

(A + µbc

∗

)

ξ = λh

∗

(A + µbc

∗

)ξ + µh

∗

(A + µbc

∗

)bc

∗

ξ =

= µ(h

∗

Ab + µh

∗

b)c

∗

ξ = µ(h

∗

Ab)c

∗

ξ.

Отсюда h

∗

Ab = 0, так как µ 6= 0, c

∗

ξ 6= 0.

Продолжая этот процесс далее, получим равенства h

∗

b = 0

(k = 0, . . . , n −1). Из полной управляемости пары (A, b) следует, что

(см.§ 1, гл.II) векторы

b, Ab, . . . , A

n−1

линейно независимы и, следовательно, из предыдущих равенств сле-

дует, что h = 0. Полученное противоречие доказывает, что предпо-

ложение о полной ненаблюдаемости пары (A, h) не верно. Лемма 1

доказана.

Лемма 2. Если прямая {αd}, α ∈ R, d ∈ R

, (d 6= 0) — инте-

гральное многообразие для системы (2), то пара (A, d) полностью

управляема.

Д о к а з а т е л ь с т в о . Из условия леммы 2 следует, что

прямая {α d} — одномерное инвариантное подпространство относи-

тельно оператора A + µbc

∗

, т.е.

(A + µbc

∗

)x = α

190

если x = αd (α, α

∈ R). Отсюда получаем

(A + µbc

∗

)

d = α

d, (4)

где k = 0, 1, 2, . . .. Из полной наблюдаемости пары (A, c) имеем

∗

d 6= 0. Действительно, в противном случае имели бы

Ad + (A + µbc

∗

)d = α

т.е. Ad = α

d и c

∗

d = 0, что противоречит полной наблюдаемости

пары (A, c). Поэтому для вектора z ∈ R

такого, что

∗

d = 0, z

∗

Ad = 0, ··· , z

∗

n−1

d = 0, (5)

будем иметь из (4) последовательно при k = 1, 2, . . . , n − 1:

0 = α

∗

d = z

∗

(A + µbc

∗

)d = µz

∗

Отсюда z

∗

b = 0, так как c

∗

d 6= 0. Далее, используя последнее равен-

ство, получаем

0 = α

∗

d = z

∗

(A + µbc

∗

)

d = z

∗

d + µz

∗

Ad+

+µz

∗

Abc

∗

d + µ

∗

d = µz

∗

Abc

∗

Отсюда z

∗

Ab = 0 (так как µ 6= 0 и c

∗

d 6= 0 ).

Продолжая этот процесс далее, получим равенства

∗

b = 0, z

∗

Ab = 0, . . . , z

∗

n−1

b = 0.

Из последних равенств и полной управляемости пары (A, b) следует,

что z = 0.

Таким образом, из соотношений (5) имеем z = 0. Это означает,

что пара (A, d) полностью управляема. Лемма 2 доказана.

Следующая теорема устанавливает стабилизируемость системы (1)

с помощью обратной связи

(

)

(6)

где s(t) — кусочно-постоянная периодическая функция с достаточно

большим периодом T .

Теорема. Пусть для системы (1) выполнены предположения ос-

новной теоремы из § 4, причем

dim M

= 1, dim L

= n − 1