Леонов Г.А., Шумафов М.М. Проблемы стабилизации линейных управляемых систем

Подождите немного. Документ загружается.

191

Пусть, далее, s

, s

и σ

— некоторые числа, причем σ

6= s

(j = 1, 2) и матрица

Q = A + σ

∗

где σ

6= s

(j = 1, 2) имеет комплексно-сопряженные собственные

значения α±iβ кратности 1, а остальные ее собственные значения

удовлетворяют условию Re λ

< α.

Тогда существует периодическая функция s(t) вида (9) (§ 4), где

σ(t) ≡ σ

, s

, σ

∈ R) такая, что система (1),(6) асимптотиче-

ски устойчива.

Д о к а з а т е л ь с т в о . Пусть h — вектор, нормальный к

подпространству L

: h⊥L

, т.е. L

= {x ∈ R

: h

∗

x = 0}. (Напом-

ним, что L

— устойчивое интегральное многообразие для системы

˙x = (A + s

∗

)x.)

Тогда из неравенства σ

6= s

, полной управляемости пары (A, b)

и полной наблюдаемости пары (A, c) по лемме 1, примененной к си-

стеме

˙x = (Q + µbc

∗

)x, x ∈ R

, (7)

где µ = s

−σ

, Q = A + σ

∗

, следует полная наблюдаемость пары

(Q, h).

Пусть теперь d — произвольный ненулевой вектор из (одномер-

ного) подпространства M

: d ∈ M

(d 6= 0). Тогда по лемме 2,

примененной к системе (7), где µ = s

− σ

, пара (Q, d) полностью

управляема.

Таким образом, для матрицы Q и векторов d и h выполнены все

условия леммы 3 из § 5. Поэтому, из этой леммы следует существо-

вание числа τ такого, что

∗

Qτ

d = 0.

Из линейности преобразования e

Qτ

следует, что e

Qτ

переводит од-

номерное подпространство M

(прямую) в некоторое подпростран-

ство (прямую)M

лежащее в L

, т.е. (рис.19)

Qτ

= M

⊂ L

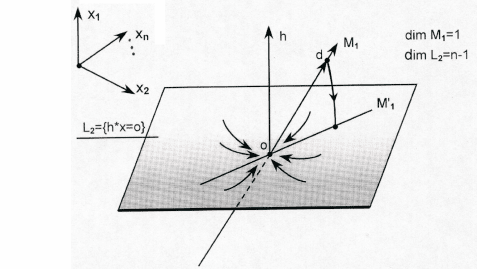
192

Рис. 19. Преобразование θ

= e

Qτ

за время τ переводит одномерное

многообразие M

в многообразие M

, лежащее в

устойчивом многообразии L

= {h

∗

x = 0}.

Тем самым выполнено "условие вложения многообразий"(здесь

= e

Qτ

, {e

} — фазовый поток системы

˙x = Qx, x ∈ R

Итак, выполнены все условия основной теоремы (§ 4). Поэтому си-

стема (1), (6) с кусочно-постоянной периодической функцией s(t)

вида (9) (§ 4), где s

, s

— некоторые числа, а σ(t) ≡ σ

, σ

∈ R,

6= s

(j = 1, 2), асимптотически устойчива. Теорема доказана.

§ 7. Проверка "условия вложения многообразий",

основанная на импульсном воздействии на

неустойчивое интегральное многообразие

В предыдущих параграфах 5 (леммы 1-3) и 6 (леммы 1, 2) были

получены эффективные условия для проверки выполнения условия

(6) из § 4, когда вращение подпространства было обусловлено нали-

чием комплексных собственных значений. Ниже мы изложим дру-

гой подход, который состоит в импульсном воздействии σ(t) = µ на

подпространство M

с большим значением |µ| на малом промежутке

времени. В этом случае вектор скорости ˙x часто оказывается близок

к вектору γb, где γ — некоторое число. Опишем этот подход более

подробно.

193

1. Импульсное воздействие на неустойчивое многообра-

зие. Рассмотрим систему

˙x = (A + µbc

∗

)x (x ∈ R

), (1)

где µ 6= 0 — большой параметр: |µ| À 1. Всюду в дальнейшем будем

считать, что b и c — одностолбцовые n-мерные векторы, s(t) в систе-

ме (8) из § 4 кусочно-постоянная скалярная периодическая функция,

пара (A, b) полностью управляема и пара (A, c) полностью наблюда-

ема.

Лемма 1. Пусть c

∗

b = 0 и для векторов h ∈ R

и d ∈ R

выпол-

нены неравенства

∗

b 6= 0, c

∗

d 6= 0.

Тогда существуют числа µ и τ (µ) > 0 такие, что

∗

x(τ(µ); d) = 0, lim

µ→+∞

τ(µ) = 0.

Д о к а з а т е л ь с т в о . Введем в рассмотрение числа

= −

∗

µh

∗

, K =

(1 + 2|µ| · kbk · kckt

)kdk

1 − (2kAkt

+ 4|µ| · kAk · kbk · kckt

)

Выберем число µ таким, что t

> 0 и

2kAkt

+ 4|µ|kAk · kbk · kckt

< 1.

(легко видеть, что левая часть этого неравенства есть O(1/µ), так

как t

= O(1/µ) ). Умножая обе части уравнения (1) на c

∗

и оценивая

∗

˙x|, будем иметь при t ∈ [0, 2t

∗

˙x(t; d)| = |c

∗

Ax(t; d)| ≤ kAkkck· max

t∈[0,2t

]

kx(t; d)k.

(Здесь x(t; d) — решение уравнения (1) с начальным условием

x(0; d) = d.) Поэтому при t ∈ [0, 2t

]

∗

x(t; d)−c

∗

d| = |c

∗

˙x(η; d)t| ≤ 2kAkkckt

max

t∈[0,2t

]

kx(t; d)k (0 < η < t).

194

Отсюда и из уравнения (1) следует, что

|x(t; d) − d − µbc

∗

d · t| =

Ax(τ; d)dτ+ µ

b[c

∗

x(τ; d)dτ−

− c

∗

d]dτ| ≤ 2kAk

+ 4|µ|kbk · kAk · kck

= (2kAkt

+ 4|µ|kAk · kbk · kckt

)

(2)

где

X = max

t∈[0,2t

]

kx(t; b)k. Используя оценку (2), получаем

kx(t; d)k ≤ kx(t, d) − d − µbc

∗

dtk + kd + µbc

∗

d · tk ≤

≤

X(2kAkt

+ 4|µ| · kbk · kckt

) + kdk(1 + 2|µ|kbk · kckt

Отсюда имеем:

X ≤ K. С учетом последней оценки из (2) получим:

∗

x(t; d)−h

∗

d−µh

∗

d·t| ≤ (2kAkt

+4|µ|·kAk·kbk·kck·t

)·khkK (3)

для всех t ∈ [0, 2t

Так как

(2kAkt

+ 4|µ| · kAk · kbk · kckt

)khkK = O(

(в силу того, что t

= O(1/µ), ), то из (3) имеем

∗

x(t; d) − h

∗

d − µh

∗

d · t| ≤ O(

). (4)

Очевидно, что h

∗

x(0; d) = h

∗

d. При t = 2t

из (4) получаем

∗

x(2t

; d) + h

∗

d| ≤ O(

Из последней оценки следует, что

∗

x(2t

(µ); d) → −h

∗

при |µ| → ∞, т.е. при достаточно больших значениях |µ | функция

(от µ) h

∗

x(2t

(µ), d) имеет тот же знак, что и −h

∗

Поскольку x(0; d) = d, то h

∗

x(t; d) меняет свой знак на отрез-

ке [0, 2t

] (при достаточно больших |µ| ). Следовательно, при до-

статочно больших |µ| существует число τ (µ) ∈ [0, 2t

] такое, что

∗

x(τ(µ); d) = 0, причем τ(µ) → 0 при µ → ∞. Лемма 1 доказана.

Лемма 2. Пусть c

∗

b 6= 0 (b, c ∈ R

), и для векторов h ∈ R

d ∈ R

выполнены неравенства

∗

b 6= 0, c

∗

d 6= 0,

∗

< 1.

195

Тогда существуют числа µ и τ (µ) > 0 такие, что

∗

x(τ(µ), d) = 0, lim

µ→∞

τ(µ) = 0.

Д о к а з а т е л ь с т в о . Введем в рассмотрение числа

µc

∗

1 −

∗

K =

[1 + kbk · kck · |c

∗

−1

(1 − e

2µc

∗

]kdk

1 − [2kAkt

+ 2kAk · kbk · kck · |c

∗

−1

(1 − e

2µc

∗

)]

Выберем число µ таким, что t

> 0 (тогда µc

∗

b < 0 ) и

2kAkt

+ 2kAkkbk · kck · |c

∗

−1

(1 − e

2µc

∗

) < 1.

(это возможно, так как t

= O(1/µ) ). Как и в доказательстве леммы

1, для решения x(t; d), x(0; d) = d уравнения (1) будем иметь при

t ∈ [0, 2t

∗

˙x(t; d) − µc

∗

b(c

∗

x(t; d))| = |c

∗

Ax(t; d)| ≤ kAk· kck ·

где

X = max

t∈[0,2t

]

x(t; d). Таким образом, функция c

∗

x(t, d) удовле-

творяет следующему дифференциальному неравенству

|˙y − ky| ≤ M, (5)

где k = µc

∗

b, M = kAk · kck

X. Решая неравенство (5) и полагая

y(t) = c

∗

x(t; d), получим при t ∈ [0, 2t

∗

x(t; d) − c

∗

µc

∗

| ≤

1 − e

2µc

∗

−µc

∗

kAk · kck ·

X. (6)

Из уравнения (1) имеем

x(t; d) − d − µb

∗

µc

∗

bτ

dτ =

Ax(τ; d) dτ +

+µb

∗

x(τ; d)c

∗

µc

∗

bτ

] dτ.

(7)

196

Оценивая последний интеграл в (7) с использованием неравенства

(6) и учитывая, что

∗

d)e

µc

∗

bτ

dτ =

∗

µc

∗

µc

∗

− 1),

получим из (7):

|x(t; d) − d −

∗

µc

∗

− 1)| ≤

≤

2kAkt

+ 2kAk · kbk · kck · |c

∗

−1

(1 − e

2µc

∗

(8)

Имеем:

kx(t; d)k ≤ kx(t; d) − d −

∗

µc

∗

− 1)k + kd +

∗

µc

∗

− 1)k.

Применяя оценку (8) к первому слагаемому в правой части по-

следнего неравенства и беря от обеих частей полученного неравен-

ства max

t∈[0,2t

]

, получаем оценку:

X ≤ K. Отсюда и из (8) следует,

что

∗

x(t; d) − h

∗

d −

∗

µc

∗

− 1)

≤

2kAkt

+ 2kAk · kbk · kck · |c

∗

−1

(1 − e

2µc

∗

)

· khkK

(9)

для всех t ∈ [0, 2t

]. Правая часть последнего неравенства есть O(1/µ),

так как t

= O(1/µ).

Как и в конце доказательства леммы 1, с учетом того, что

µc

∗

= 1 −

∗

, 1 − e

2µc

∗

2 −

∗

имеем из (9) при t = 2t

∗

x(2t

; d) + h

∗

3 −

∗

≤ O(1/µ).

Отсюда получаем при |µ| → ∞:

∗

x(2t

(µ); d) → −h

∗

3 −

∗

Учитывая, что

∗

< 1,

197

и h

∗

x(0; d) = h

∗

d, получаем, что

∗

x(0; d))(h

∗

x(2t

; d)) < 0,

т.е. функция h

∗

x(t; d) имеет (при достаточно больших значениях |µ|

) различные знаки на концах отрезка [0, 2t

]. Следовательно, суще-

ствует число τ(µ) ∈ [0, 2t

] такое, что

∗

x(τ(µ), d) = 0,

причем τ(µ) → 0 при µ → +∞. Лемма 2 доказана.

2. Случай размерности n − 1 (коразмерности 1) устойчи-

вого многообразия.

Рассмотрим теперь систему

˙x = Ax + bu, y = c

∗

x, x ∈ R

, (10)

(где A — постоянная (n × n)-матрица, b и c — одностолбцовые n-

мерные векторы) со скалярным входом u и скалярным выходом y.

С помощью леммы 1 доказывается следующая

Теорема 1. Пусть для системы (10) выполнены предположения

основной теоремы из § 4, причем

dim M

= 1, dim L

= n − 1.

Пусть, далее, c

∗

b = 0. Тогда существует обратная связь

u = s(t)y, (11)

где s(t) — кусочно-постоянная периодическая функция вида (9)

(σ(t) ≡ const ) ( § 4), что система (10), (11), т.е. система

˙x = (A + s(t)bc

∗

)x, x ∈ R

, (12)

асимптотически устойчива.

Д о к а з а т е л ь с т в о . Как и в начале доказательства теоремы

из § 6 из полной управляемости пары (A, b) и полной наблюдаемости

пары (A, c) по леммам 1 и 2 из § 6 следует полная наблюдаемость

пары (A + sbc

∗

, h) для любого числа s 6= s

и полная управляемость

пары (A + sbc

∗

, d) для любого числа s 6= s

. Здесь s

и s

— некото-

рые числа, h — вектор, нормальный к устойчивому инвариантному

многообразию (гиперплоскости) L

системы

˙x = (A + s

∗

)x (x ∈ R

198

а d — ненулевой вектор из инвариантного многообразия (прямой) M

системы

˙x = (A + s

∗

)x (x ∈ R

Отсюда следует, что h

∗

b 6= 0 и c

∗

d 6= 0. Действительно, предполо-

жим противное. Пусть h

∗

b = 0. Тогда b ∈ L

, так как h⊥L

. В силу

того, что подпространство L

инвариантно относительно оператора

A + s

∗

, будем иметь

∗

(A + s

∗

)

b = 0

при k = 1, 2, 3, . . ..

При k = 1, с учетом равенства h

∗

b = 0, имеем

0 = h

∗

(A + s

∗

)b = h

∗

Ab.

Отсюда при k = 2 получаем:

0 = h

∗

(A + s

∗

)

b = h

∗

A(A + s

∗

)b = h

∗

При k = 3, с учетом предыдущих равенств, имеем:

0 = h

∗

(A + s

∗

)

b = h

∗

A(A + s

∗

)

b = h

∗

(A + s

∗

) = h

∗

Продолжая этот процесс далее, получим при k = n − 1

0 = h

∗

(A + s

∗

)

n−1

b = h

∗

n−1

Из полученных равенств

∗

b = 0, h

∗

Ab = 0, h

∗

b = 0, . . . , h

∗

n−1

b = 0

следует, что векторы

b, Ab, A

b, . . . , A

n−1

линейно зависимы, что противоречит свойству (I

) полной управ-

ляемости пары (A, b). Следовательно, предположение, что h

∗

b = 0,

неверно. Итак, h

∗

b 6= 0.

Для установления справедливости неравенства c

∗

d 6= 0 допустим

противное: c

∗

d = 0. Тогда в силу инвариантности подпространства

относительно оператора A + s

∗

получим:

γd = (A + s

∗

)d = Ad,

где γ ∈ R. Равенства Ad = γd, d

∗

c = 0 противоречат свойству (V I

)

полной управляемости пары (A

∗

, c), или (в силу теоремы Калмана)

199

свойству полной наблюдаемости пары (A, c). Полученное противоре-

чие доказывает, что c

∗

d 6= 0.

Таким образом, выполняются все условия леммы 1 и, поэтому,

существуют числа τ и τ(µ) такие, что для системы (1) имеют место

соотношения:

∗

x(τ(µ); d) = 0, lim

µ→∞

τ(µ) = 0,

т.е. преобразование θ

τ(µ)

за время от 0 до τ(µ) переводит вектор

d ∈ M

в вектор θ

τ(µ)

d ∈ L

= {h

∗

x = 0}.

Так как преобразование θ

τ(µ)

линейно (см. следствие 3 теоремы 1

из § 2), то оно переводит подпространство M

в θ

τ(µ)

⊂ L

(см.

рис.44). Последнее означает, что выполнено "условие вложения мно-

гообразий"из § 4. Отсюда, в силу основной теоремы из § 4, вытекает

утверждение теоремы 1. Теорема 1 доказана.

Теперь, используя лемму 2, докажем следующую теорему.

Теорема 2. Пусть в системе (10)

∗

b 6= 0,

и матрица A имеет собственное значение κ > 0 и n−1 собственное

значение с вещественными частями меньшими, чем −λ, где λ > κ.

Пусть, далее, выполнено неравенство

∗

lim

p→κ

(κ − p)W (p)

< 1. (13)

(W (p) — передаточная функция системы (10)).

Тогда существует периодическая функция s(t) вида (9) из § 4 та-

кая, что система (12) асимптотически устойчива.

Д о к а з а т е л ь с т в о . В системе (1) из § 4 положим

= s

= 0. Тогда система ˙x = Ax имеет в силу условий теоремы

2 одномерное неустойчивое многообразие M (соответствующее соб-

ственному значению κ > 0 ) и устойчивое n −1-мерное многообразие

L (соответствующее собственным значениям λ

с Re λ

< −λ < 0,

j = 1, ··· , n − 1) (рис.20).

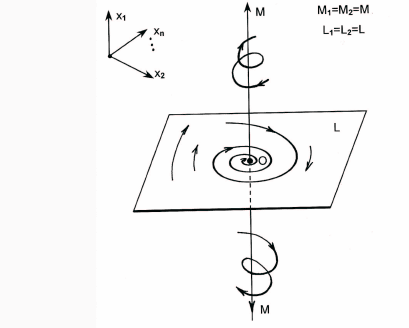
200

Рис. 20. Устойчивое L и неустойчивое M многообразия системы (1).

Не умаляя общности, можно считать, что матрица A имеет следу-

ющий вид:

A =

κ 0

0 A

, (14)

где A

— гурвицева матрица порядка (n − 1) × (n −1) (в противном

случае, к такому виду можно привести матрицу A невырожденным

преобразованием). Положим:

= L

= L, M

= M

, L

; M

, M

— интегральные многообразия, фигурирующие в усло-

виях основной теоремы из § 4). Вектор h, нормальный к подпростран-

ству L имеет вид: h = (1, 0 . . . 0)

∗

. За ненулевой вектор d ∈ M можно

взять вектор h (d := h), так как мы выбрали базис пространства

так, что матрица A имеет вид (14) и M⊥L. Представим векторы b и

c в виде

b =

, c =

где b

, c

∈ R, b

, c

∈ R

n−1

. Тогда имеем

∗

b = b

, c

∗

d = c