Леонов Г.А., Шумафов М.М. Проблемы стабилизации линейных управляемых систем

Подождите немного. Документ загружается.

221

Выберем s

так, чтобы характеристический многочлен системы (9),

где u = s

, имел вид

+ αp

+ (s

+ β)p + γ = (p − κ)(p

+ α

p + β

где α

= α + κ, β

= −γ/κ, κ > 0 и

= −β − κ(α + κ) −

Ясно, что при достаточно малых κ и, следовательно, при достаточно

больших s

, многочлен p

+α

p+ β

имеет комплексные корни −λ±iω,

где λ = (α+κ)/2. Очевидно, что при достаточно малых κ выполнено

неравенство λ > κ. Значит, все условия теоремы 1 (§ 7) выполнены.

Поскольку для системы (9)

T r (A + bs(t)

∗

) = −α ∀t ∈ R,

то в силу теоремы 2 из § 8 при α < 0 невозможна асимптотическая

устойчивость системы (9) (u = s(t)y).

Таким образом, нами получен следующий результат.

Теорема 3. Пусть α 6= 0, γ 6= 0. Тогда для стабилизируемости

системы (9) необходимо и достаточно, чтобы α > 0.

3) Пусть передаточная функция системы со скалярным входом

u(t) и скалярным выходом y(t) имеет вид

W (p) =

+ αp

+ βp + γ

где α, β, γ ∈ R, γ 6= 0. Тогда эту систему можно реализовать (в силу

следствия теоремы 2 из § 3, гл.II ) в фазовом пространстве R

как

систему вида (1) (§ 1)







˙x

= x

˙x

= x

˙x

= −(αx

+ βx

+ γx

) − u, y = x

(10)

Здесь

A =





0 1 0

0 0 1

−γ −β − α





, b =





−1





, c =









222

Стационарная стабилизация u = s

y этой системы возможна тогда

и только тогда, когда

β > 0, γ > 0.

В случае β < 0, γ < 0 стабилизация (как стационарная, так и неста-

ционарная) невозможна в силу теоремы 1 из § 8 (здесь c

= c

= 0,

= 1; a

= γ < 0, a

= β < 0).

Рассмотрим случай β > 0, γ < 0 (когда стационарная стабилиза-

ция невозможна). Применим теорему 1 из § 4. Как и выше, примем

= s

; λ

= λ

= λ, κ

= κ

= κ.

Выберем s

так, чтобы характеристический многочлен системы

(10), где u = s

y, принял вид

+ (α + s

+ βp + γ = (p − κ)(p

+ α

p + β

где κ > 0 и

= −

γ + βκ

, β

= −

, s

= −

γ + βκ

− κ − α .

При достаточно малом κ > 0 (и достаточно большом s

) мно-

гочлен p

+ α

p + β

имеет два отрицательных корня, больший из

которых равен

ν =

γ + βκ

2κ

(γ + βκ)

4κ

За число λ примем −ν : λ = −ν.

Легко проверить, что неравенство λ > κ сводится к неравенству

β + κ

> 0, которое имеет место (так как β > 0). Таким образом,

здесь (рис.23)

dim M

= dim M

= 1, dim L

= dim L

= 2.

Возьмем σ

так, чтобы характеристический многочлен системы

(10), где u = σ

y, имел вид:

+ (α + σ

+ βp + γ = (p − κ

)(p

+ α

p + β

где κ

> 0 и

= −

γ + βκ

, β

= −

, σ

= −

γ + βκ

− κ

− α.

223

Рис.23. Неустойчивое M

= M

и устойчивое L

= L

многообразия

системы (10), где u = s

При достаточно большом κ

(и |σ

|) многочлен p

+α

p+ β

имеет

комплексно сопряженные корни λ

± iω

, причем

γ + βκ

2κ

> 0.

Поэтому, не умаляя общности, можно принять (это равносильно

линейной замене координат x

, x

), что

A + σ

∗

0 Q

, b =

, c =

где Q − (2 × 2)-матрица, имеющая собственные значения λ

± iω

, c

∈ R, b

, c

∈ R

. Также (без умаления общности) можно счи-

тать, что

W (p) =

+ (α + σ

+ βp + γ

(этого можно добиться всегда за счет изменения функции s(t) в об-

ратной связи u = s(t)y для системы (10)).

Поскольку W (p) = c

∗

(A − pI)

−1

b, то

1 = lim

p→∞

pW (p) = pc

∗

(A − pI)

−1

b = − lim

p→∞

∗

(I −

)

−1

b = −c

∗

224

т.е.

∗

b = −1.

Как и в доказательстве теоремы 2 из § 7 (заменяя матрицу A на

A + σ

∗

), установим, что

lim

p→∞

(κ − p)W (p) = b

Используя последние два соотношения и вид функции W (p), будем

иметь:

∗

−1

lim

p→∞

(κ

− p)W (p)

= 1+

+ β

= 1−

2γ

−

< 1 (11)

при достаточно большом κ

Траектории системы

˙x = (A + σ

∗

)x (12)

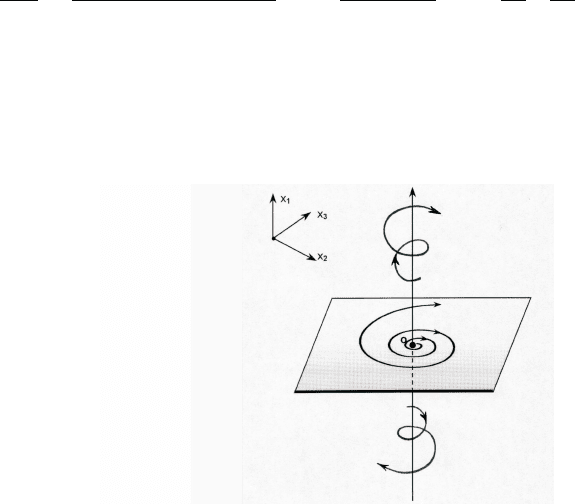
имеют вид, изображенный на рис.24.

Рис.24. Траектории системы (10), где u = σ

Так как матрица Q имеет комплексные собственные значения, то

для ненулевого вектора d ∈ M

существует число τ

> 0 такое, что

векторы









, [exp(A + σ

∗

)τ

225

принадлежат одной плоскости (следует учесть, что фазовый поток

} системы (12) аффинно эквивалентен семейству растяжений вдоль

оси x

с одновременным вращением (на угол ω

t) вокруг этой оси;

здесь f

= exp(A + σ

∗

)t).

С учетом неравенства (11) из леммы 2 (§ 7) следует существование

чисел µ и τ(µ) таких, что (в лемме 2 § 7 h

∗

:= (1, 0, 0))

(1, 0, 0) · [exp(A + (σ

+ µ)bc

∗

)τ(µ)]d

= 0,

где d

= [exp(A + σ

∗

)τ

]d.

Из того факта, что плоскости {x

= 0} и L

пересекаются и мат-

рица Q имеет комплексные собственные значения, следует существо-

вание числа τ

такого, что

[exp(A + σ

∗

)τ

∈ L

, (13)

где d

= [exp(A + (σ

+ µ)bc

∗

)τ(µ)]d

(так как плоскость {x

= 0} —

инвариантна относительно A + σ

bc, то фазовый поток {f

} в этой

плоскости есть {e

} — семейство вращений (на угол ω

t) с одновре-

менным растяжением в e

раз).

Таким образом, сначала на промежутке [0, τ

] фазовый поток {f

}

системы (12) переводит произвольный ненулевой вектор d ∈ M

вектор d

, принадлежащий плоскости π, натянутой на вектор b и еди-

ничный вектор (1, 0, 0)

∗

оси x

. Затем, переключаясь на траектории

системы ˙x = [A+(σ

+µ)bc

∗

]x, на промежутке (τ

, τ

+τ(µ)] фазовый

поток {g

} этой системы "переносит"вектор d

с плоскости π в вектор

на плоскости {x

= 0}. И, наконец, под действием опять фазового

потока {f

}(f

= e

) на промежутке (τ

+ τ (µ), τ

+ τ (µ) + τ

] век-

тор d

переводится в вектор, лежащий на пересечении {x

= 0}∪L

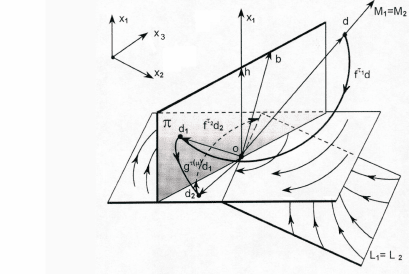
(рис.25).

226

Рис.25. Отображение неустойчивого многообразия M

в устойчивое L

Так как все преобразования f

, g

τ(µ)

, f

линейны, то из включе-

ния (13) следует включение

τ(µ)

⊂ L

т.е. выполняется "условие вложения многообразий"(6) из § 4 с

= f

τ(µ)

, τ = τ

+ τ(µ) + τ

Здесь {θ

} — фазовый поток системы

˙x = (A + σ(t)bc

∗

)x (x ∈ R

где

σ(t) =







при t ∈ [0, τ

+ µ при t ∈ [τ

, τ

+ τ(µ)),

при t ∈ [τ

+ τ(µ), τ

+ τ(µ) + τ

Итак, в силу основной теоремы из § 4 мы можем сформулировать

следующий результат.

Теорема 4. Пусть β 6= 0, γ < 0. Тогда для стабилизируемости

системы (10) необходимо и достаточно, чтобы β > 0.

227

ГЛАВА V

НЕСТАЦИОНАРНАЯ ВЫСОКОЧАСТОТНАЯ

СТАБИЛИЗАЦИЯ ЛИНЕЙНЫХ СИСТЕМ

§ 1. Постановка задачи

В этой главе рассматривается линейная система управления

˙x = Ax + bu, y = c

∗

x (1)

где A — вещественная постоянная (n × n)-матрица, b и c — одно-

столбцовые векторы: b, c ∈ R

, x = x(t) — n-мерный вектор состо-

яния (x ∈ R

), u = u(t) — скалярный вход (u ∈ R) и y = y(t) —

скалярный выход (y ∈ R).

В предыдущей главе было дано в ряде важных случаев решение

задачи нестационарной линейной стабилизации для системы (1) —

проблемы Брокетта — в классе кусочно–постоянных периодических

стабилизирующих функций s(t), т.е. была найдена такая обратная

связь

u = s(t)

∗

y, (2)

что замкнутая система (1), (2), т.е. система

˙x = (A + bs(t)

∗

)x, x ∈ R

оказывалась асимптотически устойчивой. При этом период T функ-

ции s(t) был достаточно большим, т.е. нами была осуществлена низ-

кочастотная стабилизация системы (1) (и при более общей ситуации,

когда b и c тоже матрицы).

В работе [259] предложен подход к решению проблемы Брокетта

в другом классе стабилизирующих функций s(t), а именно, в клас-

се непрерывных периодических функций, у которых период доста-

точно мал (высокочастотная стабилизация). Эта методика отлична

от методики, рассмотренной в предыдущей главе и основывается на

процедурах усреднения.

228

Следует отметить, что этот подход использует идеи и методы,

применявшиеся ранее в теории управления колебаниями (см., на-

пример ([169,193,195,196,257]), в частности, при рассмотрении хоро-

шо известного явления стабилизации верхнего положения маятника,

когда точка подвеса совершает достаточно быстрые колебания в вер-

тикальном направлении (см. [23,31,77,114,128,169,235]).

Изложим указанный выше подход, применяемый для решения (в

частном случае, когда b, c ∈ R

) проблемы Брокетта, следуя работе

[259].

§ 2. Некоторые предварительные факты.

Приведем некоторые понятия и факты, которые будут использо-

ваны нами в дальнейшем.

1. Теорема об экспоненциальной устойчивости.

Пусть дана система

˙x = f (t, x), t ∈ R, x ∈ R

, f(t, 0) ≡ 0, (1)

где вектор-функция f(t, x) = (f

(t, x), ··· , f

(t, x))

∗

кусочно-непре-

рывна по t в интервале I

= {a

< t < +∞} (a ∈ R) и удовлетворяет

условию Липшица по переменным x

, ··· , x

во всем пространстве

, x = (x

, ··· , x

)

∗

О п р е д е л е н и е . Тривиальное р е ш е н и е x(t) ≡ 0 диффе-

ренциального уравнения (1) называется э к с п о н е н ц и а л ь н о у с-

т о й ч и в ы м при t → +∞ (см. [81]), если для каждого решения

x(t) ≡ x(t; t

, x

), x(t

) = x

, x

∈ R

этого уравнения справедливо

неравенство

kx(t)k ≤ N kx(t

−α(t−t

)

при t ≥ t

где N и α — положительные постоянные, не зависящие от выбора

решения x(t).

Аналогично определяется экспоненциальная устойчивость нетри-

виального решения. А именно, решение ξ(t) экспоненциально устой-

чиво, если для любого решения x(t) ≡ x(t; t

, x

) справедливо нера-

венство

kx(t) − ξ(t)k ≤ N kx(t

) − ξ(t

)ke

−α(t−t

)

при t ≥ t

229

где N и α — положительные постоянные, не зависящие от выбора

решения x(t).

Очевидно, что из экспоненциальной устойчивости решения

x(t) ≡ 0 следует его асимптотическая устойчивость в целом. Обрат-

ное, вообще говоря, неверно. Примером может служить скалярное

уравнение

˙x = −

, x ∈ R, t ∈ [1, +∞).

Действительно, его общее решение имеет вид

x(t) =

, x

= x(1), (t

:= 1);

и, поэтому, нулевое решение x(t) ≡ 0 не является экспоненциально

устойчивым, хотя оно является асимптотически устойчивым.

Однако, для линейной системы с постоянными коэффициентами

положение иное: из асимптотической устойчивости ее тривиального

решения следует его экспоненциальная устойчивость.

Предложение 1. Если тривиальное решение линейной системы

˙x = Ax, x ∈ R

, (2)

с постоянной матрицей A асимптотически устойчиво (при

t → +∞), то эта система экспоненциально устойчива, т.е. каж-

дое ее решение экспоненциально устойчиво (при t → +∞).

Д о к а з а т е л ь с т в о. В силу теоремы 1 из § 1, гл.III тривиальное

решение x(t) ≡ 0 системы (2) асимптотически устойчиво тогда и

только тогда, когда матрица A гурвицева, т.е. все собственные числа

(A) матрицы A имеют отрицательные вещественные части:

Re λ

(A) < 0 (j = 1, . . . , n).

Положим

α = −

max

Re λ

(A).

Тогда по лемме ( § 2, гл.I) об оценке нормы экспоненты имеем

k ≤ N e

−αt

при t ≥ 0, (3)

где N — некоторая положительная константа.

230

Решение x(t) уравнения (2) с начальным условием x(t

) = x

да-

ется формулой

x(t) = e

(t−t

где начальные данные t

∈ R, x

∈ R

произвольные.

Поэтому, с учетом оценки (3), получаем

kx(t)k ≤ N kx(t

)ke

−α(t−t

)

при t ≥ t

Пусть ξ(t) — любое решение системы (2). Тогда, учитывая, что

разность x(t) − ξ(t) тоже есть решение системы (2), будем иметь

kx(t) − ξ(t)k ≤ N kx(t

) − ξ(t

)ke

−α(t−t

)

при t ≥ t

Последнее соотношение доказывает предложение 1.

Почти очевидно следующее

Предложение 2. Линейная система

˙x = A(t)x, x ∈ R

с кусочно-непрерывной матрицей A(t) экспоненциально устойчива

тогда и только тогда, когда ее тривиальное решение x(t) ≡ 0 экс-

поненциально устойчиво.

Д о к а з а т е л ь с т в о аналогично доказательству теоремы 4 из § 1,

гл.III.

Приведем одно достаточное условие экспоненциальной устойчиво-

сти общей системы (1).

Сначала докажем следующее простое утверждение.

Лемма. Пусть

q(x) = x

∗

Qx (Q = Q

∗

— положительно определенная квадратичная форма, заданная в R

Тогда существуют положительные числа α < β такие, что

αkxk

≤ q(x) ≤ βkxk

Д о к а з а т е л ь с т в о. Форма q(x) положительна во всех точках

единичной сферы kxk = 1. Поскольку сфера компактна, а форма

q(x) непрерывна на ней, то точные нижняя и верхняя грани дости-

гаются, и, поэтому

0 < α ≤ q(x) ≤ β, для всех x ∈ {x : kxk = 1}, (4)