Лекции - В.Л.Пантелеев Курс лекций Теория фигуры Земли

Подождите немного. Документ загружается.

Для дальнейшего упрощения полученной интегральной формулы воспользуемся так

называемой

теоремой сложения сферических функций.

Пусть точка имеет постоянные координаты, а точка принадлежит элементу

поверхности и имеет штрихованные координаты. Обозначим центральное

расстояние между этими двумя точками греческой буквой

. Тогда теорема

сложения для нормированных сферических функций выглядит так

(4.19)

Теперь формулу (

4.18) можно переписать следующим образом

(4.20)

Каждое слагаемое в полученной формуле часто называют

функциями Лапласа

(4.21)

Лекция 5. Аналитическое представление

гравитационного потенциала

• 5.1 Разложение гравитационного потенциала в ряд Лапласа

• 5.2 Посточнные Стокса

• 5.3 Механический смысл стоксовых постоянных

• 5.4 Потенциал тяжести

• 5.5 Пределы Пуанкаре и Крудели для угловой скорости вращения. Фигуры равновесия

5.1 Разложение гравитационного потенциала в ряд

Лапласа

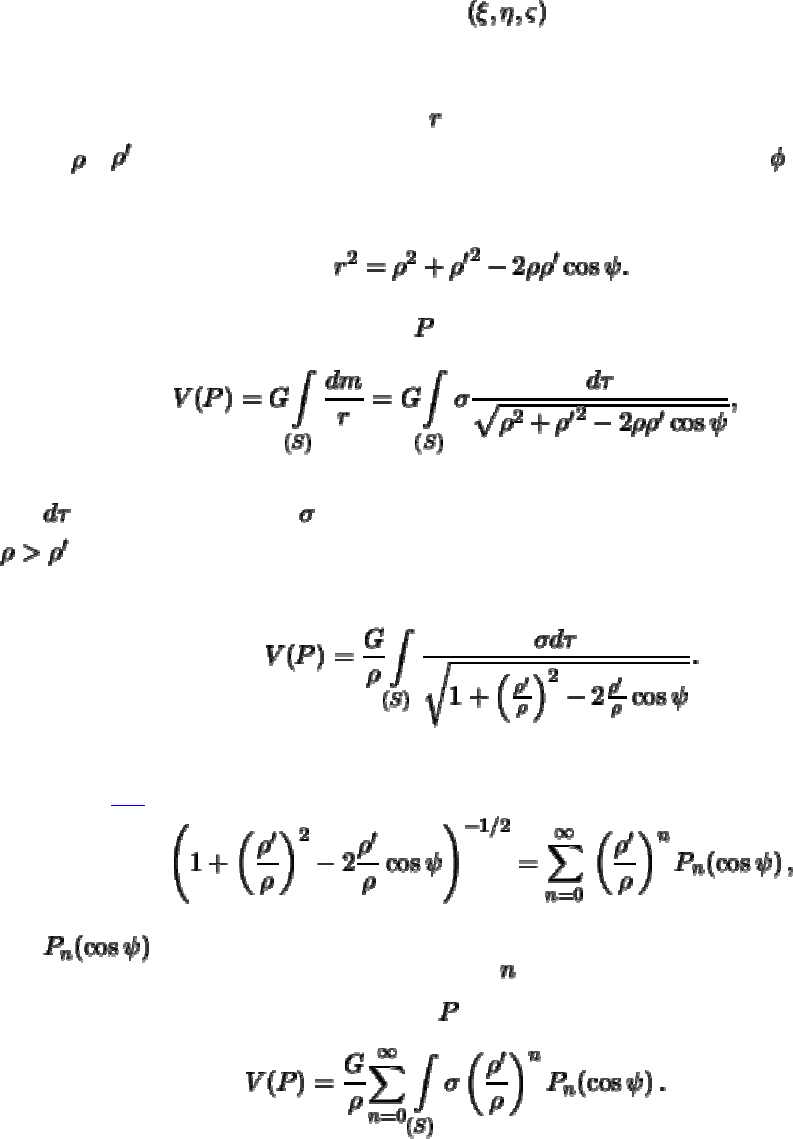
Напомним, что под потенциалом какой либо силы, в том числе и

силы тяжести

мы

будем понимать

силовую функцию

. Для начала остановимся на потенциале

сил

притяжения

, который чаще всего называют

гравитационным потенциалом

. Пусть

элемент массы

находится в точке

, а точка

P(x,y,z)

с фиксированными

координатами находится вне притягивающего тела. Радиус-вектор, соединяющий

точки

, будем обозначать через , а радиус-векторы этих точек соответственно

через

и . Угол между этими векторами будем обозначать через . Если точка

- начало координат, то из треугольника

ОРQ

следует

Потенциал притяжения тела в точке

имеет вид

(5.1)

где

-- элемент объема, -- плотность. Вынесем из-под знака корня величину

, получим

Под знаком интеграла стоит производящая функция полиномов Лежандра (см.

формулу (

4.1)), поэтому

где

-- полином Лежандра степени .

Теперь потенциал притяжения в точке

принимает вид

(5.2)

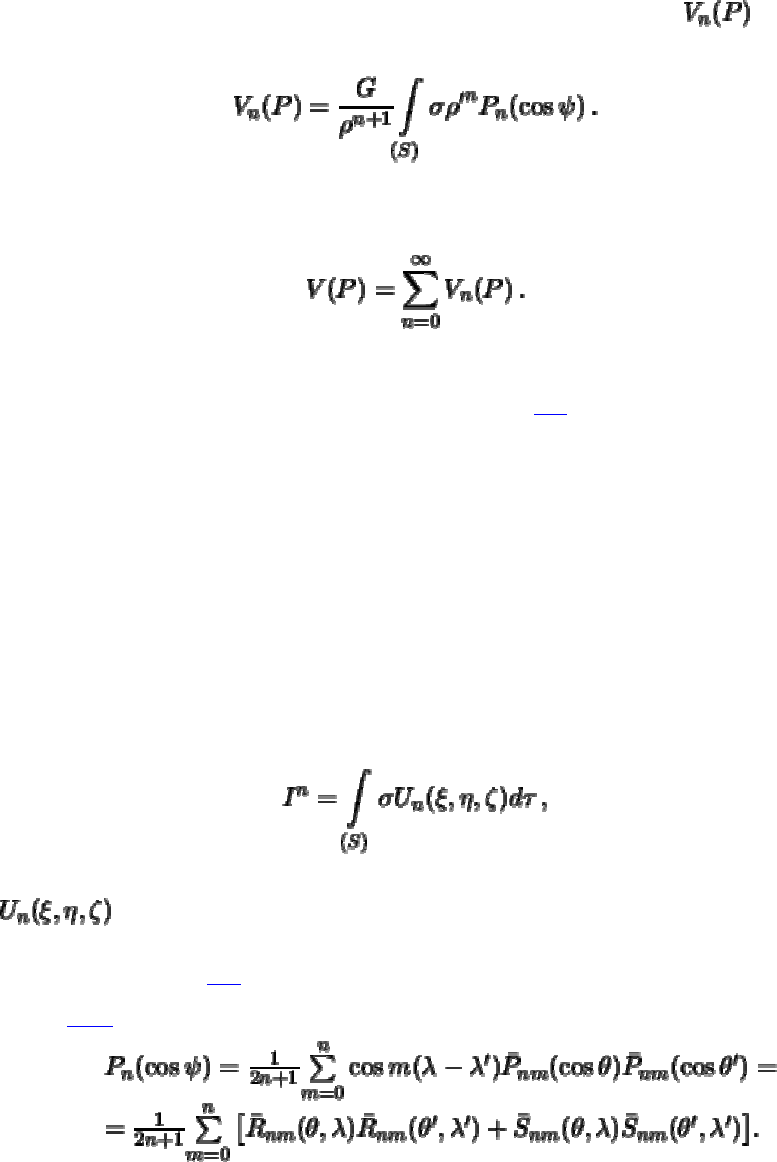
Каждое отдельное слагаемое полученной формулы есть функция Лапласа для

потенциала притяжения во внешней точке. Обозначив ее через

, получим

(5.3)

Теперь ряд Лапласа можно записать так

(5.4)

Функции Лапласа, как следует из формулы (

5.3), зависят от распределения

плотности внутри притягивающего тела. Приведенный интеграл есть постоянная

величина, которая, в свою очередь, определяется с помощью так называемых

постоянных Стокса, или, стоксовых постоянных.

5.2 Посточнные Стокса

Постоянной Стокса называется величина, которая определяется следующим

образом

(5.5)

где

гармоническая функция внутри объема интегрирования.

Вернемся к формуле (

5.3). Воспользуемся формулой сложения гармонических

функций (

4.19). Ее, очевидно, можно переписать следующим образом

Следовательно

(5.6)

Функции текущих (штрихованных) координат

и являются

гармоническими, так как они принадлежат к шаровым функциям первого типа.

Следовательно, по определению (

5.5) интегралы вида и

являются стоксовыми постоянными.

Введем обозначения

(5.7)

Здесь, как несколько позже убедимся,

-- масса тела,

-- постоянная, имеющая

размерность длины, а

и безразмерные постоянные Стокса.

Теперь функцию Лапласа для потенциала притяжения во внешней точке

Можно представить следующим образом

(5.8)

Суммируя по всем

, получим искомое разложение потенциала притяжения в ряд

Лапласа

(5.9)

Все рассуждения мы провели для нормированных функций, отмечая их чертой

сверху. Однако эти же рассуждения справедливы и для ненормированных функций.

В этом случае постоянные Стокса будут иметь несколько иной вид. Опуская

выкладки, приведем лишь окончательную формулу

(5.10)

где

при и при .

5.3 Механический смысл стоксовых постоянных

Рассмотрим сначала случай, когда . Тогда и , так как эта переменная

изменяется от нуля до

. Поскольку гармоника также равна нулю, остается

определить только

. Из формулы (5.10) следует

(5.11)

Рассмотрим теперь случай, когда

. Теперь мы должны определить четыре

стоксовых постоянных: , , , . Обращаясь к формуле (5.10), получим

(5.12)

(5.13)

Для того, чтобы выполнить интегрирование, нужно перейти к декартовым

координатам

(5.14)

По определению сферических гармоник имеет место равенство

(5.15)

При

имеем , поэтому

Из теоретической механики известно, что координаты центра масс тела

определяются следующим образом

поэтому

(5.16)

Итак, шаровая функция первой степени, которую представляет собой функция

Лапласа первой степени, определяет центр масс притягивающего тела. Определим

теперь функцию Лапласа второй степени. Из формулы (

5.7) следует

Снова перейдем к декартовым координатам

(5.17)

Следуя правилам теоретической механики, выполним интегрирование. Будем

использовать традиционные обозначения для моментов массы второго порядка --

моментов инерции

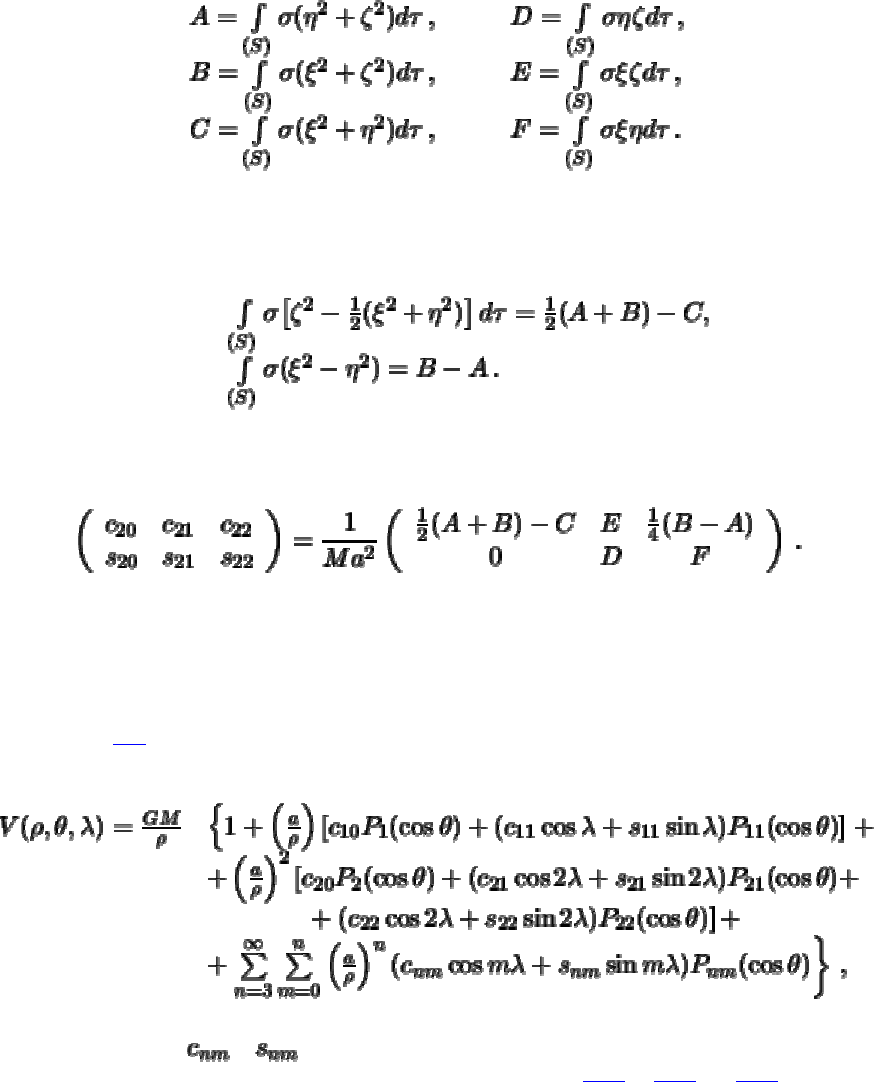
(5.18)

Для того, чтобы привести формулу для коэффициентов к окончательному виду,

заметим, что

Следовательно, матрицу, составленную из коэффициентов разложения потенциала

притяжения для шаровой функции второй степени, можно представить в виде

(5.19)

Вернемся к формуле представления гравитационного потенциала рядом Лапласа.

Определяя стоксовы постоянные через ненормированные шаровые функции,

формула (

5.9) будет иметь тот же вид, за исключением того, что стоксовы

постоянные и сферические функции "потеряют" черту сверху

(5.20)

где коэффициенты

и определяются формулами (5.10), (5.16) и (5.19). Полученную

формулу можно упростить, если принять

1. начало координат совпадает с центром масс,

2. направление осей совпадают с главными осями инерции.

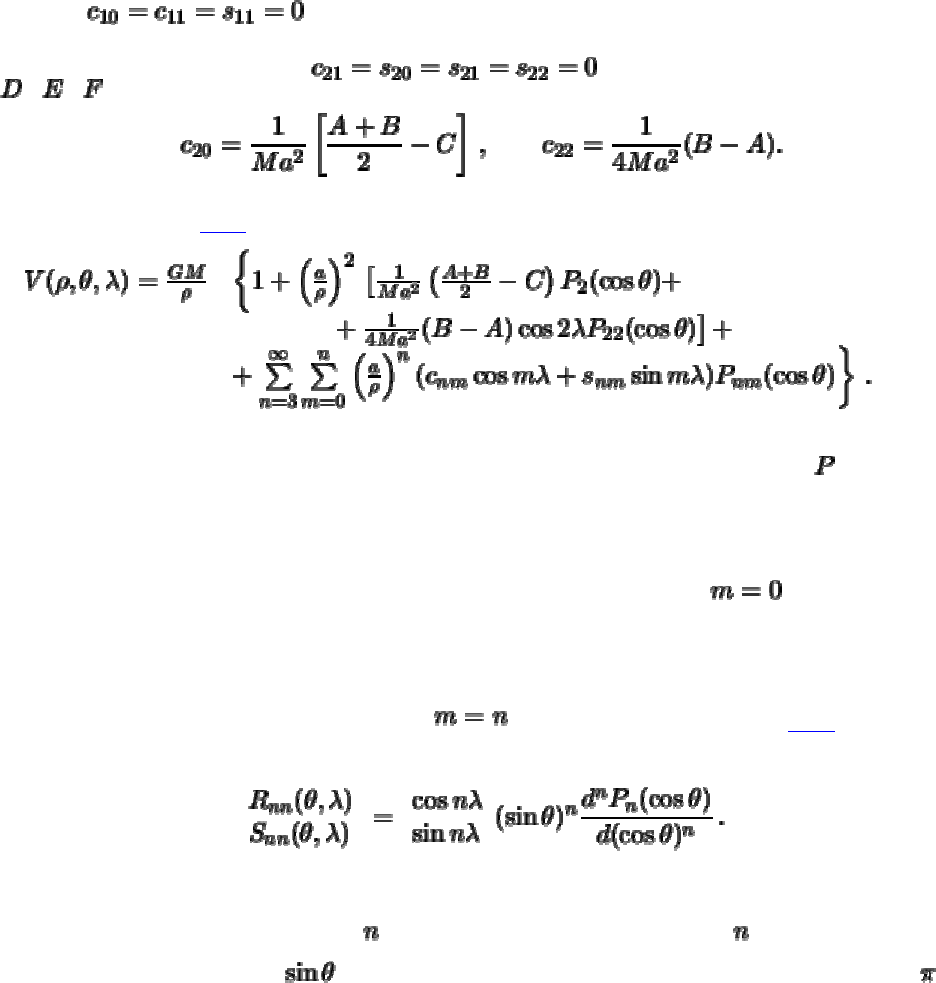
При выполнении этих условий функция Лапласа первой степени будет равна нулю,

то есть

. Кроме того, будут равны нулю и

произведения инерции

, , . Следовательно, , а

Теперь формула (

5.20) принимает вид

(5.21)

Полученная формула говорит о том, что потенциал притяжения в точке

зависит как

от расстояния рассматриваемой точки от начала координат, так и сферических

координат: полярного расстояния и долготы. Однако отдельные сферические

гармоники могут зависеть только от широты, например, при

, в этом случае

гармоники называют

зональными

. Поверхность сферы в этом случае оказывается

разбитой на зоны -- сферические пояса.

Второй крайний случай возникает при . Обратимся к формуле (5.15). В этом

случае она приобретает вид

Нетрудно понять, что знак сферическая гармоника может менять при определенных

значениях долготы, так как

-ая производная полинома -ой степени есть

постоянная величина, а

при изменении полярного расстояния от нуля до не

меняет знака. Поверхность сферы оказывается разбитой подобно арбузу на сектора

и соответствующие гармоники, называются

секториальными.

Наконец, в остальных случаях границы изменения знака сферической гармоники на

поверхности сферы образуют мозаику подобно шахматной доске. Эти гармоники

называют

тессеральными

от латинского слова

tessera

, что означает сферический

четырехугольник в мозаике.

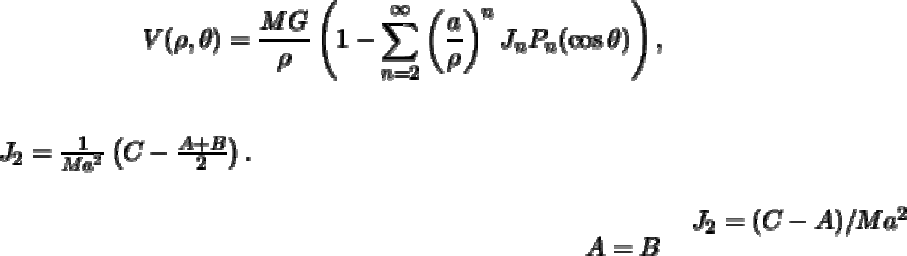
Для многих задач небесной механики силовую функцию планеты аппроксимируют

только зональными гармониками. В этом случае мы предполагаем, что

рассматриваемая планета есть тело вращения и зависимость силы притяжения от

долготы точки, для которой берется силовая функция, отсутствует. Тогда

гравитационный потенциал записывают в виде

(5.22)

где

Эту постоянную относят к фундаментальным постоянным.

Если планета представляет собой тело вращения, то

и .

Она зависит лишь от моментов инерции, то есть от моментов масс второго порядка.

Остальные коэффициенты называют мультипольными моментами массы. Они не

имеют столь ясного механического смысла.

5.4 Потенциал тяжести

Силовую функцию удельной силы тяжести обычно называют потенциалом силы

тяжести. Под

силой тяжести

часто понимают силу, с которой всякое тело

притягивается к Земле (см., например, Л.В.Сорокин "Гравиметрия и

гравиметрическая разведка", Гостоптехиздат, М., 1953). Молчаливо предполагается,

что это тело имеет массу, равную единице. Поэтому речь идет об

удельной

силе

тяжести. Кроме того, наблюдения за действием силы проводятся во вращающейся

вместе с Землей системе координат, то есть в неинерциальной системе отсчета. На

пробное тело, если нет специальных оговорок, действуют лишь две физические

силы: сила притяжения со стороны Земли и упругая сила реакции опоры.

Результирующая этих двух сил не равна нулю. Суммы их дает как раз ту силу,

которая сообщает пробному телу

ускорение

, с которым тело совершает движение по

круговой траектории в процессе суточного вращения. Согласно третьему закону

механики пробное тело взаимодействует с опорой, оно давит на опору с той же

самой силой, что и опора давит на тело. Тяжесть пробного тела создает реакция

опоры (подставки). Эту силу называют

весом

тела. Очевидно, что вес тела есть сила,

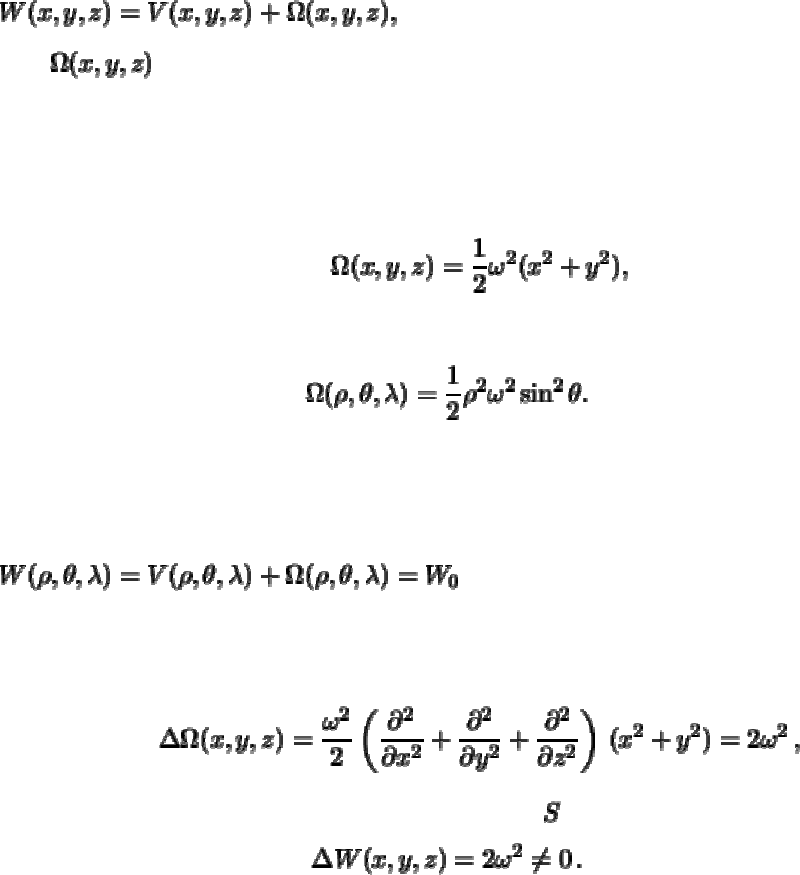
равная равнодействующей силы притяжения и силы инерции, которую принято

называть

центробежной

силой. Итак, удельная сила тяжести есть вес тела

единичной массы, неподвижной относительно поверхности Земли (или какой-либо

другой планеты). Удельная сила имеет размерность ускорения, поэтому часто

вместо термина

удельная сила тяжести

говорят

ускорение

силы тяжести. На

английском языке ускорение силы тяжести называют gravity, на немецком --

schwehre, в обоих случаях эти слова обозначают

тяжесть

Для того, чтобы записать потенциал силы тяжести, необходимо потенциал силы

притяжения сложить с силовой функцией для центробежной силы. Эту силовую

функцию в дальнейшем будем называть

потенциалом тяжести

где -- силовая функция для центробежной силы инерции, которую мы

условно будем называть центробежным потенциалом. Если ось

Оz

выбрать так,

чтобы она строго совпадала с осью вращения Земли, то центробежный потенциал

будет иметь вид

или в сферических координатах

(5.23)

Поверхностью уровня, то есть поверхностью равного потенциала

(эквипотенциальной поверхностью) называют поверхность, имеющей уравнение

В отличие от потенциала притяжения потенциал тяжести не является гармонической

функцией, ибо

поэтому вне тела, ограниченного поверхностью

, будет иметь место равенство

(5.24)